基于培养学生逻辑思维能力的课例
——以(沪科版)九年级(上)23.1锐角的三角函数教学为例
☉安徽省淮北市杜集区教育局教研室 朱启州
☉安徽省淮北市杜集区实验初级中学 李 丽
本文大胆尝试在半径为1的圆内定义锐角三角函数,意在突出三角函数的几何意义,突出数学核心思想方法——数形结合法,引导和启发教师研究教村,基于核心素养进行教学.
现有教材大都以相似三角形为基础,建立锐角三角函数的概念,教学中的难点是让学生理解三角函数值只与角的大小有关,与角所在的三角形的大小无关.突破这一难点,常常需要花费较大的精力.为此,笔者大胆尝试在半径为1的圆内定义锐角三角函数,从而绕过教学难点,又继承了现有教材锐角三角函数知识体系,拓展了学生的思维空间.下面是笔者在这方面的一点实践探索,供读者参考.
一、利用半径为1的圆定义锐角三角函数的教学课例与点评
1.创设情境,激趣引新
问题1:汽车免不了爬坡,爬坡能力是衡量汽车性能的重要指标之一,汽车的爬坡能力是指汽车在通常情况下满载时所能爬越的最大坡度.怎样描述坡面的倾斜程度呢?
师:如图1和图2,直线a是水平线,A1B1、A2B2分别表示两个不同的坡面,哪个更陡?你是怎样想的?

图1

图2
生1:图2中的坡面A2B2更陡,因为它与水平面的夹角更大.
师:准确地说,坡面与水平面所夹的锐角越大,坡面越陡,我们把这个角称为坡角.还有哪些不同的方法,能说明后者更陡吗?
生2:在坡面上走相同的路程,升的越高坡面越陡.
师:好的,在生活中,我们都这样认为.谁能用数学语言,把意思表达清楚吗?
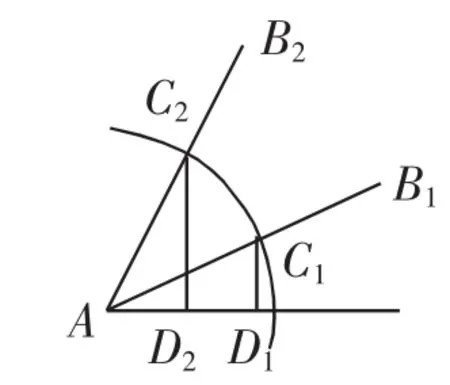
生3:如图3和图4,分别在A1B1、A2B2上取C1、C2,使A1C1=A2C2,作垂线段C1D1、C2D2,有C1D1 图3 图4 点评:这是沪科版教材中的一个引例,此例来自于生活,为学生熟悉并且与本课教学联系密切.这种从日常生活中衡量坡面陡峭程度的问题出发,经过数学化将问题转化为数学问题,再借助数学的方法去解决问题.这种“用数学的眼光观察问题,用数学的思维去发现问题,用数学的方法去处理问题”就是数学理性. 师:(追问)为什么要在坡面上取C1、C2? 生4:若是土坡,你能到地下的水平线上取点吗?(理直气壮) 师:值得肯定的是,这位同学还考虑到实际情况.也就是说,如果就是一面内的两个角,还是可以的,对吗?(学生都认可这个说法) 师:A1C1=A2C2都取1个单位长,行吗? 生:当然可以.(有部分学生只是默认) 师:那老师再将两个角叠在一起,顶点与始边(始边在水平线上)重合,如图5,以A为圆心,单位1为半径画圆,分别交两角的终边于C1、C2,C1D1、C2D2分别是到水平线的垂线段,同学们观察图形,有什么发现? 点评:我们常常想,这一点是学生的真实想法吗?是自然生成的吗?这一点是不容置疑的,因为为了比较哪个坡更陡,只要比较在坡面上移动相同的距离时,上升的高度越高的坡越陡,于是用在坡面上移动一个单位的距离时最为方便.上述念头就会由然而生. 生5:我发现C1D1 生6:我发现线段C1D1、C2D2的大小与坡角一样,也能表示坡面的陡缓程度. 生7:我发现一个锐角只能画出图中的一条垂线段. 生8:我发现一个锐角与图中的垂线段是一一对应的. 图5 图6 师:大家观察的真仔细,表达得也很好.如图6,在半径为1的圆中,锐角α始边为ON,终边与圆只有一个交点P,垂线段MP对角α而言是唯一的,对吧.所以我们把垂线段MP的长度叫角α的正弦,记作:sinα=MP. 把线段OM的长度叫角α的余弦,记作:cosα=OM. 点评:引入中教师将引例中的两个角叠合在一起,从而让两个不相关联的图形产生了联系,图形由静态变为动态,有效引导学生进行数学推断和理解三角函数的几何意义.数学作为人类文化的一部分,它的知识、方法、思想、语言、精神等,是人类理性思维的根. 问题2:利用半径为1的圆,求30°角的正弦、余弦值. 师:5位同学到黑板前板演,其余同学在纸面上完成. 师:请5位同学分别给板演的5位同学批阅,并给出评价.然后将其中一位同学的解答用实物投影仪展示在屏幕上. 图7 解:如图7,在Rt△OMP中,∠POM=30°,OP=1,则由勾股定理,可得OM 问题3:一个15°的角,在放大100倍的放大镜下看,它的正弦、余弦、正切值会变吗?为什么? 生1:可能会变,因为放大后这个角就不是15°. 生2:不会变,因为放大后的图形与原图形相似,所以这个角还是15°. 师:一个说会变,一个说不会变,老师认为说的都在理,那该听谁的呢? 生3:不会变,画图就知道了,就当黑板上角α就是15°,放大后只是边画长了,角不会变,PM、OM、NQ都只有一个,所以它的正弦、余弦值不会变. 师:说的太好了!刚才谁说的会变,你来反驳几句. 生1:是我错了,当时我没想清楚,心想一放大,角说不定会怎样变. 师:数学是最讲诚信的,真理会越辩越明. 点评:练习的重要目的是为了诊断与反馈,进而进行必要的矫正与深化,达到“生饭做熟,熟饭做透”的目的.令人意想不到的是学生的作为溢出教师的教学预设,这就是宝贵课堂生成资源,教师因势利导地让学生争辩,潜移默化地进行了社会主义核心价值观的教育. 师:对锐角α,如图8,sinα=MP,cosα=OM. 通过观察,你能发现锐角α的三角函数哪些结论?并简单说明理由. 生1:很显然sinα、cosα都是正数. 图8 生2:我发现0 生3:我发现1 生4:我发现sin2α+cos2α=1,在Rt△OMP中,OM2+MP2=OP2,而OP=1,所以sin2α+cos2α=1. 师:同学们真能干,发现这么多结论,这些都是同角三角函数关系. 师:如果锐角α逐渐增大,那么sinα、cosα、tanα是怎样变化的? 生5:sinα随锐角α的增大而增大;cosα随锐角α的增大而减小.至于为什么,观察图形是一目了然的. 师:同学们观察的真仔细,有些连老师都没想到,你们真了不起. 点评:从三角函数的几何意义出发,借助数形结合,很容易理解锐角三角函数的一些重要性质,更进一步理解三角函数的意义,这种注重精确、定量、逻辑推理的思维方式就是数学理性. 师:时间过得真快,又到快下课的时间了.想一想,这节课你学到了什么?有哪些感受?你们还有什么疑问或没明白的地方,大胆说出来. 生1:我知道锐角的正弦、余弦意义,了解到它们的一些性质,会计算一些特殊角的正弦、余弦值等. 生2:我知道斜坡的锐角的正弦、余弦与坡角一样,也能反映坡面的陡缓程度;还知道锐角的正弦、余弦值只与角的大小有关. 生3:课前我依课本预习过,不是这样说的,但都是殊途同归,这节课让我长见识了. 师:真是一个爱学习的好孩子,预习是一个好习惯.还有哪些同学也预习了?(30多位同学都举起了手) 师:大家谈的都很实际,说明我们都是有思想的人.老师想让大家课后把本课所学的知识用思维导图的形式表达出来,好吗?看谁画的更清晰、明了、有价值. 点评:数学应用环节,教师充分发挥学生的主动性,引导学生自主思考、充分交流、充分发表见解,教师充分发挥引领作用,将师生之间的合作这一宝贵资源用到极致,学生在思想交流与碰撞中收获自信与快乐,学生脸上洋溢着成功的喜悦. 有诗云:“好雨知时节,当春乃发生.随风潜入夜,润物细无声.”教师通过情境的创设,诱发学生思考冲动,在生生、师生交流中激发出智慧火花,在教师的引领下,通过学生积极运用数学工具进行理性思考,在思考中学生不断获得新的认识,新的学习成果,这就是真实的数学课堂.话又说回来,不是每节课都能实现同样的结果,也许下节课面对不一样的学生,不会产生要借助单位圆定义三角函数,而会产生不一样的念头,不得而知.正所谓:一生一世界,一课一乾坤. 1.吴之季,苏淳.义务教育教科书·数学(九年级上册)[J].上海:上海科学技术出版社,2012. 2.崔群,孙朝仁.初中数学实验实物类工具开发的基本原则[J].中学数学(下),2015(9). 3.朱启州.一堂数学“翻转”复习课引发的思考[J].中学数学(下),2015(9).H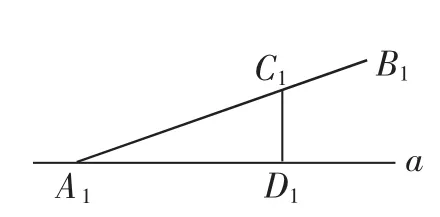

2.自然探究,由然而生

3.巩固练习,升华认识

4.引伸拓展,出井观天

二、结束语

