关注三“点”：平行四边形起始课教学与思考

☉江苏省昆山市葛江中学 周晓秋

平行四边形的起始课教学一直是各级教研热点课题，很多地区赛课、研讨课、示范课常常选此课题，很多期刊上也有这节课的教学实录与教学反思.笔者近期有机会开设该课的教学研讨课，参考了一些文献、或网络（QQ群）、或网上视频课，并融入自己的一些思考，本文梳理该课的教学流程，并跟进思考，提供研讨.

一、教学过程

教学环节1：创设情境，引入新课

复习旧知：我们学习平面几何有一段时间了，最熟悉的是什么图形？除了一般的三角形，我们还学习了特殊的三角形，有哪些特殊三角形呢？以等腰三角形为例，我们学习了等腰三角形的哪些内容？通过三角形的学习，积累了经验与方法.学习了三角形之后，你们认为应该学习什么图形？除了一般的四边形还要学习什么？

教学预设：在提问上述旧知时，随着学生的互动对话，学生对三角形进行了系统的学习，以特殊三角形——等腰三角形为例，引导学生回顾等腰三角形的学习经历，明确几何图形的研究思路：定义——性质——判定——应用.引导学生类比三角形的特殊化，学生容易想到特殊的四边形.在黑板上渐次生成如下板书：

展示图片：在生活中有这样一种特殊四边形（如图1、2），认真观察，如果把图形抽象出来，是什么图形？

图1

图2

教学预设：教师展示图片，从实际情境中抽象出数学模型，激发学习兴趣；确定本节课研究对象为平行四边形，引出本课课题“平行四边形”.

教学环节2：画图活动，给出定义

给出定义：小学的时候，同学们已经认识了平行四边形，怎样的四边形才是平行四边形呢？

教学预设：学生回忆小学所学平行四边形知识，教师板书定义：两组对边分别平行的四边形叫作平行四边形.

画图活动：你能根据定义画出一个平行四边形吗？

学生画图的同时，教师在黑板上板演作图（如图3）.

图3

教学预设：教师类比三角形，指出平行四边形的记法和读法.刚才我们用文字语言和图形语言表示了平行四边形的定义，我们也可以用符号语言来表示平行四边形的定义.

认识平行四边形的要素：邻边、对边、邻角、对角、对角线.

回顾小学阶段平行四边形的定义，画图感知平行四边形.

追问：知道了平行四边形的定义，接下来我们应该继续学习什么呢？

教学预设：通过平行四边形的定义、记法、读法的学习，引导学生在文字语言、图形语言和符号语言间进行相互转化.体会定义的双重性，既可以作为平行四边形的性质，又可以作为判定平行四边形的依据.

教学环节3：猜想发现，证明性质

提问：我们应该从哪些角度，来研究平行四边形的性质呢？观察刚才画出的平行四边形，猜想平行四边形的边、角具有什么数量关系？请独立思考，并写出你猜想的结论.类比等腰三角形，确定平行四边形的研究方向，从定义出发，再研究性质.

教学预设：图形性质是研究图形的构成要素——边、角之间的关系.平行四边形边的位置关系在定义中已有所体现，重点研究边、角之间的数量关系.学生通过观察度量，提出猜想，先独立思考，再小组讨论，教师及时参与并指导.然后展示猜想，教师板书学生的猜想.

学生根据已有的学习经验，容易用到度量操作验证、对称操作验证、推理论证等方法.教具展示对称操作验证的过程，说明平行四边形是中心对称图形.

由于上述问题比较开放，教师需要对“平行四边形的对边相等”这条猜想进行推理论证的教学预设是：如果学生提出连接对角线，教师追问：为什么要连接对角线？如果学生找不到证明思路，教师引导学生由结论（证明线段相等）出发，分析达到目标的方法（通过三角形全等证明边、角相等），需添加辅助线，构造全等三角形，将四边形问题转化为三角形问题来解决.

在初步形成证明思路之后，学生独立推理证明，适当安排学生上台板书，并规范证明过程.讲评时，鼓励学生展示他们证明角相等时的不同方法，并跟进反思“殊途何以同归”.

教学环节4：性质应用，例题讲评

例1 如图4，四边形ABCD是平行四边形.

（1）若∠B=50°，则∠A=___°，∠C=___°，∠D=___°.

（2） 若AB=2cm，BC=3cm，则▱ABCD的周长为_____cm.

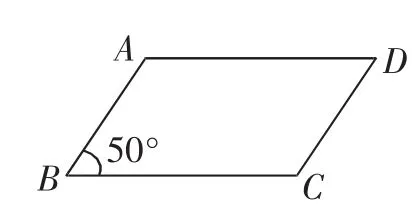
图4

图5

例2 如图5，在▱ABCD中，E、F为对角线BD上的两点，且BE=DF.

求证：AE=CF.

教学预设：学生先独立完成，然后进行展示，说明理由，巩固性质.对于例2，学生独立思考，先行证明，教师巡视并作个别指导.然后再找一位同学展示证明思路与证明过程，鼓励不同做法，最后总结方法.总结证明线段相等的方法，除了全等三角形，利用平行四边形的性质也是证明线段或角相等的又一重要工具.

教学环节5：课堂小结，梳理反思

预设如下小结问题：

（1）本节课你学到了哪些知识？

（2）探究性质经历了哪些过程？体会到哪些数学思想方法？

（3）对于平行四边形，你认为还要研究哪些内容？

教学组织：让学生回顾思考，积极交流展示，在此基础上，教师总结：本节课，我们类比等腰三角形的学习，按照“定义——性质——判定——应用”的研究思路，学习了平行四边形的定义和性质.通过“观察——猜想——验证”的研究方法，将四边形问题转化为三角形问题，探究出了平行四边形边、角的性质.与此同时，我们看到，类比和转化等数学思想方法是研究几何图形的有力手段.在师生小结的基础上，完善形成板书（见下面“板书设计”）.

附：板书设计

平行四边形的性质（第1课时）一、定义两组对边分别平行的四边形叫作平行四边形.【例题讲评区】研究思路：定义-性质-判定-应用A D B研究方法：四边形类比转C化三角形记作：▱ABCD二、性质1.平行四边形的对边相等.2.平行四边形的对角相等.思想方法：观察-猜想-验证

二、教学思考

1.深刻理解教学内容，找准知识生长点

备课之初，我们需要对教学内容深入理解，包括全面研习国家层面的课程标准、不同版本的教材上这部分内容的素材，以及对平行四边形第1课时的内容划分.比如，学生在小学阶段就学习平行四边形，但初中学段对平行四边形的要求是不一样的，按张奠宙先生所说“小学阶段学习数学是‘消费’数学，而到了中学，就要开始‘还债’，追问理由，进行推理论证”.这也是平面几何学习的价值或精神所在.找准知识生长点之后，可以从学生熟悉的生活图片（富含平行四边形的图片）引入新课，抽象出平行四边形，从定义出发画图直观感受并猜想和证明相关性质.成为这节课新知引入和探索的逻辑链条.

2.精准研究班情学情，明确教学用力点

经常借班上课的老师会有这样的感受：相同的内容在不同的班级（即学情不同）上出来的效果往往相差甚大.可见精准研究班级学生的学情，即学生的最近发展区对于明确教学用力点是十分关键的.在上文课例中，我们针对本班学情，“舍弃”了有些教材上在第1课时学习的“平行线之间的距离”这个知识点，而用力点放在师生互动对话探究出平行四边形的性质，让平行四边形性质的证明与思想方法的感悟得到了时间保证.

3.选配典型例题习题，聚焦训练发力点

平行四边形的性质一共两课时，第1课时研究平行四边形的定义及平行四边形边、角的性质；第2课时研究平行四边形对角线的性质，并应用性质解决简单问题.本节课是第1课时，主要从边、角两方面探究平行四边形的性质，进一步积累几何图形的研究思路和研究方法，在探究中将四边形问题转化为三角形问题，对于培养演绎推理、训练数学思维、积累活动经验等方面起到重要作用.由于本课在探索并证明平行四边形的性质上所需教学时间较多，所以例题教学环节就不宜选配太难的习题，这不仅仅是因为平行四边形起始课、新授课的要求，更主要的是要突出本课的课时教学目标（掌握平行四边形的边、角性质）.顺便提及，当下有些“习题单”式的导学案，混淆了新授课、起始课、习题课的教学目标，在学习一个新概念、新性质的起始阶段，就选配了很多“好题、难题”，反而“败坏”了学生的学习兴致，把本来很简单、美妙的数学概念或性质，变成“面目可憎”的难题的习题教学.这是值得我们反思的.

1.刘东升，沈红艳.经营转场：折纸串起平行四边形起始课教学［J］.中学数学（下），2016（10）.

2.郑毓信.“开放的数学教学”新探［J］.中学数学月刊，2007（7）.

3.章建跃.构建逻辑连贯的学习过程使学生学会思考［J］.数学通报，2013（6）.H