光学三维扫描仪光强传递函数的测量和校正

张 旭，邵双运，祝 祥，宋志军

(北京交通大学 理学院，北京 100044)

1 引 言

光学三维测量是光学(Optics)、微电子学(Microelectronics)、信息学(Informatics)以及应用数学(Applied Mathematics)等学科交叉发展和融合的成果[1]。光学三维轮廓测量技术具有非接触、高分辨率、无破坏、数据获取速度快等优点[2]。因此，光学三维轮廓测量技术在机器视觉、自动加工、工业在线检测、产品质量控制、实物仿形、生物医学等领域具有重要意义和广阔的应用前景。利用光学三维测量技术，获取三维面形信息的测量方法基本可以分为两大类：被动三维传感和主动三维传感[3]。典型的主动三维传感方法有飞行时间法、光学三角法和相位测量法等。根据相位检测方法的不同，相位测量法主要分为莫尔轮廓术(Moire Topography,MT)、傅里叶变换轮廓术(Fourier Transform Profilometry，FTP)和相位测量轮廓术(Phase Measuring Profilometry，PMP)。

相位测量轮廓术是采用正弦光栅投影和相移技术相结合的一种方法[4-5]。相移(Phase Shifting或Phase Step，PS)法是相位检测技术的重要方法。将规则光栅图像投射到三维漫反射被测物表面，从另一角度可以观察到由于受物体高度的影响而引起的条纹变形。通过计算被测物表面某点的相位值，再根据此相位值就可计算出该点的高度值。因此相位计算的准确性直接影响了高度计算的准确性[6]。

由于测量系统非线性响应的存在，变形条纹中会出现高次谐波，这将导致计算所得的相位中出现周期性的变化，对高度测量结果带来较大的误差[7-8]。因此必须对测量系统进行非线性校正，减少高次谐波带来的误差。Guo等人提出一种适用于数字条纹投影轮廓术的伽玛校正技术[9]。该技术基于条纹图像的统计分析，由条纹图像的归一化累积直方图来估计伽玛值，再通过设定γ常数生成待投射的数字光栅，从而校正这种输出光强与驱动信号之间非线性关系。Cao等人提出一种基于数字微镜(Digital Micromirror Device，DMD)的相位轮廓测量系统的非线性校正技术[10-11]。为获得投影系统的光强传递函数，在同一帧投影条纹图像上由计算机编码产生0到255的线性的灰度级，并由CCD图像传感器采集，在将采集到的图像光强与输入的光强比值为该系统的光强传递函数ITF，并以查找表的方式隐式存入计算机。投影的光栅在理想平面上试探性的设置一个预期的正弦光场，然后将光场以像素单位离散化，通过查找表，找出对应该像素单元的输入灰度值，若输入输出灰度级具有一一对应的关系，则对该输入灰度进行编码，其输出就是正弦光场分布。

上述两类校正技术均采用有限的几帧图像估计投影系统的强度传递参数，Guo的方法需要不断地进行迭代，进行伽玛估计和相位评估，最终得到实际的伽玛值；Cao的方法用灰度连续分布的一帧图像求解整个系统的全局灰度曲线，由于投影系统各部分的响应并不完全一致，不可避免地会带来参数估计误差。

本文采用光强传递函数来描述光强信号的传递过程，通过逐一投射不同灰度的图像，分析投影系统输入灰度级与输出亮度之间的对应关系，测量出系统的光学强度传递信号，分析其非线性效应，基于反函数变换得到系统的光强传递函数的校正函数，利用该校正函数计算输入光栅图像并投射，提高了光学三维扫描仪的测量精度。

2 投影系统光强传递函数的测量与校正

2.1 三维扫描测量系统

本文所用的光学三维扫描测量系统原理如图1所示，系统由一台LCD投影仪，一台CCD摄像机，一块标准平板和一台计算机构成。

图1 光学扫描仪系统结构图 Fig.1 Structure of optical profilometry system

测量时，计算机控制投射装置(LCD投影仪)按照测量需求投射光栅条纹，CCD摄像机采集参考面上的条纹图和被测物表面的条纹图，由计算机处理这些条纹图，从中抽取出相位信息，并由相位与高度关系恢复出物体高度。

2.2 投影系统光强传递函数的校正

投影系统的光强传递函数的校正过程如图2所示，校正过程分两大步骤：(1)输入线性光强信号，投影仪投射到光屏的信号为非线性信号，用光功率计接收投出的信号，再经过归一化和拟合处理后，得到投影系统的光强传递函数即投影系统的输出输入关系函数；(2)对得到的光强传递函数进行逆运算，求其反函数，得到输入输出关系函数，当输出为0到1的线性输出时，求解输入信号大小，最后根据输入信号函数得到待投射的光栅图像。

图2 光强传递函数校正流程 Fig.2 ITF′s calibration process

在本文实验中，编程生成256张16 bit的灰度图片，灰度从0变化到255，以255为间隔等距抽样，再将灰度图像通过LCD按顺序投射出来，形成一个线性的数字输入信号。利用光功率计测量LCD投影仪输出的光强信号，得到LCD投影仪的光强传递函数的测试曲线[12]，具体数字信号的传递过程如图3所示。

图3 信号传递过程示意图 Fig.3 Signal transfer process

通过光功率计测得的LCD投影仪的光强传递函数曲线如图4所示。

图4 数字投影系统归一化光强传递函数曲线 Fig.4 Normalized ITF curve of digital projection system

可以看出，对于计算机输入的线性变化的光强信号，光功率计接收到的信号的光功率曲线不是线性变化的，这说明LCD投影仪具有非线性输出的响应特性，因此，如果直接对LCD投影仪输入标准的正弦光栅信号，由于LCD投影仪光强传递函数的影响，输出的信号将不再是标准的正弦型光栅信号。

对图4信号进行高阶拟合，可得公式:

P=-0.454 6x4+1.002 2x3+

0.443 5x2+0.083 1x-0.010 3

对上式做反函数变换，可得到输入输出关系函数。其输出值在(0,1)之间的数值解如表1所示，所得反函数曲线如图5所示。该图表示当投影仪的输出为线性变化，即输出值为(0,1)之间线性变化，其输入的灰度变化情况。该函数曲线即为投影仪的光强校正函数曲线。

表1 反函数数值解表

图5 反函数曲线(即 ：数字投影系统光强校正函数曲线) Fig.5 Inverse function curve(namely ITF′s calibration curve of digital projection system)

3 实验验证

3.1 校正效果验证

本文采用两种方法验证了提出的校正方法的有效性。

(1)利用校正函数生成一组预期输出为线性光强分布的256张灰度图片，输入的灰度变化如图5所示，经投影系统投射，再利用光功率计接收，得到输出的光强曲线，归一化处理后得到图6所示光强分布，可以看出，经过校正后，LCD输出的灰度等级为线性。

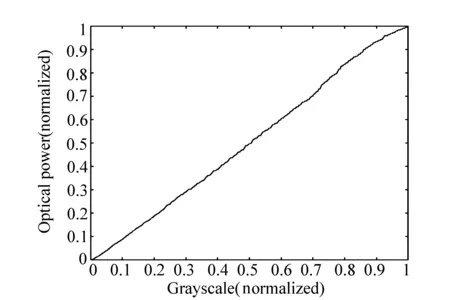
图6 校正后LCD投影仪线性输出 Fig.6 Linear output of LCD projector after calibration

(2)利用实验获得的数字投影仪光强传递校正函数对输入的正弦信号进行校正，得到输入的非正弦光栅图像，如图7(b)所示，再用LCD投影仪投影，用相机拍摄投影的条纹，得到输出信号，并与不经过校正的原始正弦光栅输出进行比较。结果如图7所示。

由图7可以看出，未经过校正时，用投影仪投射，则光功率计接收到的正弦光栅信号发生形变，上小下大，不是标准正弦信号。经过校正后，光功率计接收到的正弦光栅信号接近标准。为了分析信号的正弦性，对图信号分别做傅立叶变换，结果如图7(e)、7(f)所示。对于校正前输入的正弦信号，只含有基频，不含有高次谐波，投到待测平面上，接收到的信号中出现了明显的二次谐波和其它高次谐波；对于校正后的正弦输入信号，其输出信号的高次谐波被有效抑制，从而降低了系统非线性响应所带来的高次谐波误差。

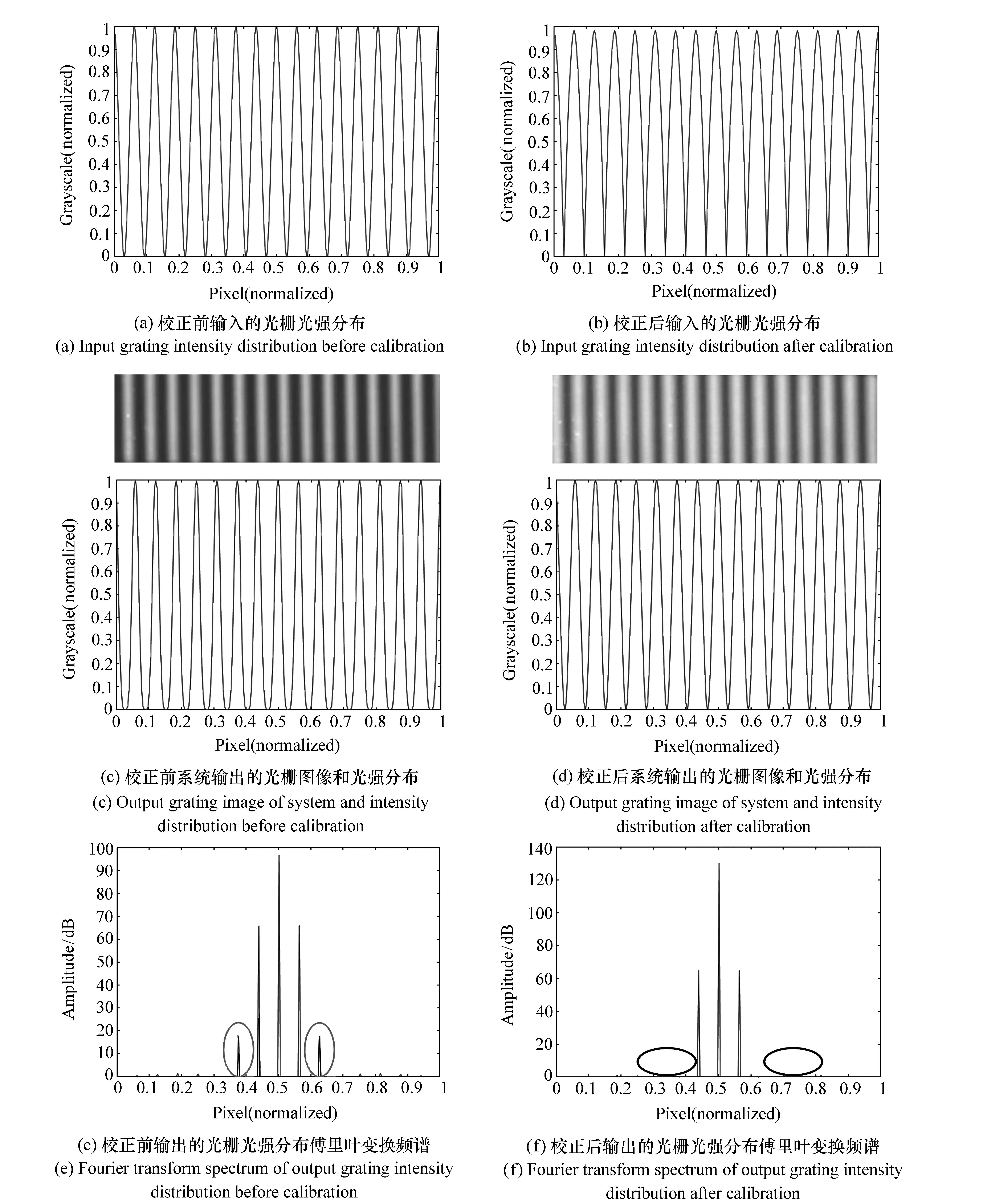
图7 灰度校正结果 Fig.7 Gray level calibration results

3.2 实物测量

为进一步说明校正的效果，采用等间隔满周期算法(正弦光栅20像素，5步相移算法)构建三维测量软件。测量系统利用校正前的光栅和校正后的光栅分别进行标定，然后分别测量标准平板和标准量块，比较测量结果的差异。

3.2.1 标准平板的测量

将标准平板垂直于测量系统CCD的光轴方向放置，用精度为10 μm的精密移动平台带动平板沿CCD光轴方向进行平移，每次移动20 mm，共移动8次，得到9个平面位置。保证测量环境不变的情况下，在9个位置点分别投射校正前和校正后的正弦光栅，求出相应位置处的高度值，和标准移动距离比较计算误差，其结果如表2和图8所示。

表2标准平板测量结果

Tab.2Measurementresultsofstandardpanel(mm)

123456789标准020406080100120140160校正前0.1118.6739.1659.3379.50101.02119.35138.84160.10误差0.111.330.840.670.501.020.651.160.1校正后-0.2921.2239.7360.0879.86101.05119.17140.89160.22误差0.291.220.270.080.141.050.830.890.22

图8 误差对比 Fig.8 Error comparison

由表1和图8可知，校正前的平均绝对误差为0.71 mm，校正后的平均绝对误差为0.55 mm，部分位置误差偏大的原因，初步分析是由于电动平移台的控制误差以及待测平板与移动方向不垂直造成的。

3.2.2 标准量块的测量

对厚度均匀的标准块用游标卡尺测量两个台阶平面的厚度，其厚度差作为这两个面的高度差，取其平均值12.20 mm作为量块厚度的真值。在同样条件下，三维测量系统采用校正前的光栅和校正后的光栅对标准块分别进行测量，结果如表3所示, 测量精度提高了3.75%。

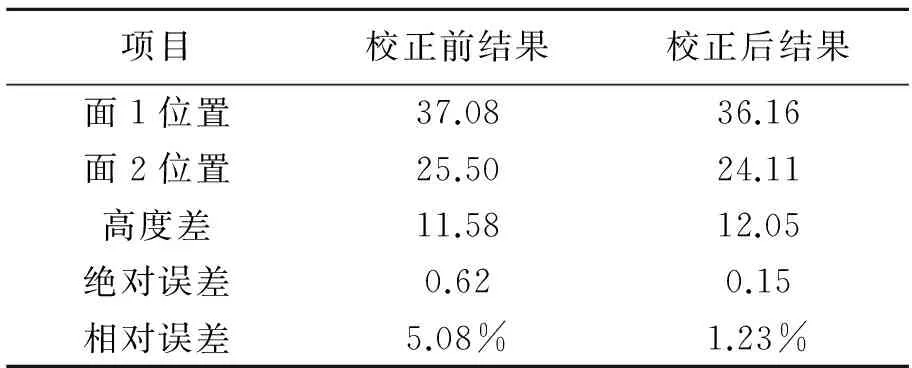
表3 标准量块测量结果比较

3.2.3 小结

前述两个实验结果明显表明，经过校正后的测量系统位置测量精度高于校正前的测量精度，标准量块的校正后的测量结果优于校正前的测量结果，说明本文提出的光强传递函数校正方法可以有效提高测量系统的测量精度。校正后，用该测量系统对实际物体进行测量，其测量精度优于校正前的测量精度，充分证明了该方法在实际测量中的有效性。

4 结 论

本文提出了一种新的光学三维测量系统数字光栅投影仪的光强传递函数测量和校准方法，首先测量了数字投影仪输入灰度级与输出亮度之间的非线性关系。对于输入的线性信号，测得光栅投影仪在线性输入下的光强传递函数，并利用逆向变换求得光强传递校正函数，以此校正了数字投影仪的光强传递函数的非线性。Guo等人提出的方法需要不断的进行迭代，以求得实际伽玛的值。Cao等人提出的方法，由于投影系统各部分响应不完全一致，容易造成参数估计误差。本文提出的方法只需对投影系统的光强传递函数进行校正，进而即可校正数字投影仪的非线性响应，方法具有简便性和适用性。对于标准平板的测量，校正前平均误差为0.71 mm，校正后平均误差为0.55 mm,对于标准量块测量，校正前误差为0.62 mm，校正后误差为0.15 mm，测量精度提高了3.75%。实验结果证实了校正方法的有效性。

[1] 牛小兵.光栅投射三维轮廓测量技术的研究[D].天津:天津大学,2003.

NIU X B. 3-D Profilometry based on grating projection[D]. Tianjin:Tianjin University,2003.(in Chinese)

[2] CHEN F,BROWN G M,SONG M. Overview of three-dimensional shape measurement using optical methods[J].Opt.Eng.,2000,39(1):10-22.

[3] 金国藩.激光测量学[M].北京:科学出版社,1998:798-800.

JIN G P.LaserMeasurement[M]. Beijing:Science Press,1998:798-800.(in Chinese)

[4] 张万祯.数字投影结构光三维测量方法研究[D].浙江:浙江大学,2015.

ZHANG W ZH. Structured-light three dimensional measurement method based on digital projector[D]. Zhejiang:Zhejiang University,2015.(in Chinese)

[5] 马淑贞.光学三维位相轮廓测量技术研究[D].昆明:昆明理工大学,2003.

MA SH ZH. Studies on a optical three-dimension phase profilometry measurement technology[D]. Kunming:Kunming University,2003.(in Chinese)

[6] 安东,陈李,丁一飞,等.光栅投影相位法系统模型及标定方法[J].中国光学,2015,8(1):248-254.

AN D,CHEN L,DING Y F,etal.. Optical system model and calibration of grating projection phase method[J].ChineseOptics,2015,8(1):248-254.(in Chinese)

[7] 李万松.位相测量轮廓术(PMP)应用研究[D].四川:四川大学,1999.

LI W S. Applied Study on Phase Measuring Profilometry(PMP)[D]. Sichuan:Sichuan University,1999.(in Chinese)

[8] 邵双运,苏显渝,等.结构光场的非正弦性对调制度测量轮廓术精度的影响[J].激光杂志,2004,25(1):26-28.

SHAO SH Y,SU X Y,etal.. The influence of non-sinusoidal signal on the measurement precision of MMP[J].LaserJournal,2004,25(1):26-28.(in Chinese)

[9] GUO H W,HE H T,CHEN M Y. Gamma correction for digital fringe projection profilometry[J].AppliedOptics,2004,43(14):2906-2914.

[10] 曹益平.基于数字微镜的位相测量轮廓术[D].四川:四川大学,2003.

CAO Y P. Digital Micromirror Device Based Measuring Profilometry[D]. Sichuan:Sichuan University,2003.(in Chinese)

[11] CAO Y P,etal.. Intensity transfer function of DMD and its application in PMP[J].ProceedingsofSPIE,2002,4778:83-88.

[12] 武迎春,曹益平,肖焱山.任意相移最小二乘法迭代的在线三维检测[J].光学 精密工程,2014,22(5):1347-1353.

WU Y CH,CAO Y P,XIAO Y SH. On-line three-diemensional inspection using randomly phase-shifting fringe based on least-square iteration[J].OpticalandPrecisionEngineering,2014.22(5):1347-1353.(in Chinese)

[13] 肖焱山,曹益平,等.基于傅里叶频谱分析的相位测量轮廓术系统Gamma非线性校正方法[J].光学学报,2012,32(12):1-6.

XIAO Y SH,CAO Y P,etal.. Gamma nonlinearity correction based on Fourier spectrum analysis for phase measuring profilometry[J].OpticsJournal,2012,32(12):1-6.(in Chinese)

[14] 许平.提高数字光投影傅里叶变换轮廓术精度的方法研究[D].四川:四川大学,2006.

XU P. Study on improving the precision of FTP based on DLP projector[D]. Sichuan:Sichuan Unversity,2006.(in Chinese)

[15] 杨丽霞.光栅投影三维形貌测量系统的研究[D].辽宁:东北大学,2012.

YANG L X. Research on the system of grating projection three-dimensional profilometry[D]. Liaoning:Northeastern University,2012.(in Chinese)

[16] 费东,苏显渝,李杰林.PMP中的液晶投影器的性能研究[J].光电工程,1996,23(5):18-22.

FEI D,SU X Y,LI J L. Research on performance of liquid crystal display in phase measuring profilometry[J].Opto-ElectronicEngineering,1996,23(5):18-22.(in Chinese)

[17] 郝煜栋,赵洋,李达成.光栅投影式轮廓测量中两种误差的分析[J].光学学报,2000,20(3):376-379.

HAO Y D,ZHAO Y,LI D CH. Analysis of two errors in grating projection profilometry[J].OpticsJournal,2000,20(3):376-379.(in Chinese)

[18] 李万松,苏显渝,等.非恒定环境光条件下的相位测量剖面术[J].光学学报,2000,20(5):617-623.

LI W S,SU X Y,etal.. Phase-measuring profilometry in non-constant environmental light[J].OpticsJournal,2000,20(5):617-623.(in Chinese)