Grating diffractive behavior of surface plasmon wave on meta-surface

WANG Xue-fei, LU Zhen-wu, WANG Tai-sheng , YU Wei-xing

(1.Changchun Institute of Optics,Fine Mechanics & Physics,Chinese Academy of Sciences,Changchun 130033，China；2.University of the Chinese Academy of Sciences,Beijing 100049,China;3.Xi′an Institute of Optics and Precision Mechanics,Chinese Academy of Sciences,Xi′an 710119,China)

1 Introduction

引 言

Surface Plasmon Polariton wave(SPP) is an electron density wave with collective oscillation generated by the interaction between photons and free electron on the metal surface. It can gather electromagnetic field energy in a small space[1], which has shown great potential in the field of nanophotonics and has become a hotspot in the research of nanophotonics[1]. SPP has been hailed as the most promising information carrier for integrated nano-photonic devices and has been widely used in many fields such as nano-lithography, new energy sources, highly sensitive biochemical sensing, solar cells and high-efficiency photonic components[2-5]; SPP has also an important application in the area of super-resolution imaging. Yang Jingzhong, use light soure with wavelength of 7 μm to illuminate a graphene nanocavity on metasurface to excite the SPP wave, and generate a standing wave with wavelength of 52 nm by interference. When this standing wave is applied to a microscope illumination source[6], the resolution of the microscope can reach 26 nm, which is nearly 100 times of the conventional fluorescent microscope.

表面等离激元激化波(Surface Plasmonic Polariton Wave,SPP)是光子和金属表面的自由电子相互作用所产生的集体振荡的电子疏密波，它能够将电磁场的能量聚集在一个很小的空间范围内[1]，在纳米光子学领域显示出了巨大的应用潜力，并成为当前纳米光子学研究的热点。SPP被誉为当前最有希望的纳米集成光子器件的信息载体，并已被广泛地应用在纳米光刻、新型能源、高灵敏生物化学传感、太阳能电池以及高效光子元器件等诸多领域中[2-5]。SPP在超分辨成像中也有重要应用，杨靖忠利用波长7 μm的光源入射到超表面的石墨烯纳米腔结构激发SPP波，干涉产生了波长为52 nm的驻波。将该驻波应用到显微镜的照明光源时，显微镜分辨率可达到26 nm,比传统荧光显微镜提高了近100倍左右[6]。

As a device to excite SPP, the metal grating has a simple structure and is easy to control, so it is widely used to generate SPP waves[7].

金属光栅作为激发SPP的器件，结构简单且易于控制，被广泛应用于SPP波的产生[7]。

The SPP wave is an electromagnetic wave and is essentially the same as the spatial light wave thus possess characteristics of interference and diffraction. A number of nanodevices, such as super-lenses, have been developed by using the diffractive properties of SPP waves. In recent years, the research on the diffraction of SPP waves has been increasing. R. Ziaetal. studied the effects of the width of the metallic waveguide on the diffraction of the SPP wave at the waveguide end when they conducted Young′s double-slit experiment of SPP waves and found that the SPP wave is not diffracted at the waveguide end face if the waveguide width is smaller than a critic value[8]. Feng Liangetal. focused SPP wave on the metal surface by using its near-field diffractive property, and found that the electric field strength of the focusing point was increased by three times[9].

SPP波在本质上与空间光相同，为电磁波，因此具有干涉及衍射特性。利用SPP波的衍射特性已经制作出了很多纳米器件，例如超透镜等。近年来对SPP波衍射特性的研究不断增多。R.Zia等人在做SPP波的杨氏双缝实验时，研究了金属波导的宽度对SPP波在波导端部衍射现象的影响，并发现存在一个极限值，当波导宽度小于这个值时，SPP波在波导端面不发生衍射[8]。冯亮等人在金属表面上利用SPP波的近场衍射现象对其进行聚焦，使聚焦点的电场强度增大了3倍之多[9]。

The near-field diffraction phenomenon of SPP waves on the metal surface is mainly affected by the structural parameters such as the period and filling factor of the diffraction grating. However, only few work have been reported in this area. In this paper, we use the metallic grating couple method to excite SPP waves, and studied the influence of diffraction grating on the near-field diffraction phenomenon of SPP wave. We found that of SPP wave has an obvious diffractive effect in near-field. The spatial light is transformed into SPP wave, and the spectral signal can be separated at the micro-nanoscale by optimizing the structural parameters of the diffraction grating.

SPP波在金属表面的近场衍射现象主要受衍射光栅的周期、占空比等结构参数的影响，然而鲜见关于这方面的公开报道。本文利用金属光栅耦合方式激发SPP波，研究了衍射光栅对SPP波近场衍射现象的影响，并发现SPP波的近场衍射有分光作用。将空间光转变成SPP波，通过优化衍射光栅的结构参数，可以实现在微纳尺度上对光谱信号的分离。

2 Surface plasmon resonance theory and three characteristic lengths of SPP waves

表面等离子体共振理论及SPP波的3个特征长度

SPP wave is a kind of electromagnetic wave propagating along the metal/dielectric interface formed by the coupling of the surface charge group′s oscillation and the electromagnetic field on the metal/dielectric interface[10]. The SPP field intensity component is maximum at the metal/dielectric interface and decays exponentially on both sides of the interface. In the visible and near-infrared wave bands, the real part of the dielectric constant of most metals is negative, so the sign of dielectric constant of the metal and its neighboring dielectric medium is opposite, and only P-polarized light(TM) can excite SPPs. As shown in Fig.1, when light(including P-polarized light) is incident on the metallic grating, diffraction occurs on the grating surface, and different diffraction angles correspond to different diffraction orders. According to the grating equation, it can be seen that the component of the wave vector of them-th(m=±1,±2,±3,…，±n) order diffracted light in the direction parallel to the interface is

Fig.1 Cross section of rectangular metal gratings in one-dimension 图1 一维矩形金属光栅横截面

SPP是金属/介质界面上由表面电荷的集体震荡与电磁场耦合所形成的沿着金属/介质界面传播的一种电磁波[10]。SPP的场分量在金属/介质界面上取得最大值，在金属两侧的介质中场分量呈e指数衰减。在可见光及近红外波段内，绝大多数金属介电常数的实部为负数，因此金属的介电常数与其相邻介质的介电常数异号，只有P偏振光(TM)才能激发出SPP。如图1所示，当光波(含P偏振光)入射到金属光栅时，在光栅表面将发生衍射现象，不同的衍射角度对应于不同的衍射级次。根据光栅方程可知第m(m=±1,±2,±3,…，±n)级衍射光的波矢在平行于界面方向上的分量如式(1)。

(1)

Wherek0is the light wave vector in free space,θis the incident angle of the light wave,ε2is the dielectric constant of the medium, andΛis the grating period. It can be seen from equation (1) that the wave vector of the diffracted light can be increased due to the diffraction of the grating so that the wave vector of them-th order diffracted light parallel to the interface can be equal to the wave vector of the SPP wave at the interface, that is

式中,k0是自由空间光波波矢，θ为光波的入射角，ε2为介质的介电常数，Λ为光栅周期。从式(1)可知，光栅的衍射作用可以使衍射光的波矢得到增大，从而可以使平行于界面的第m级衍射光波矢分量与界面上SPP波的波矢相等，即有式(2)。

(2)

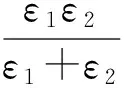
As can be seen from the formula (2) ，the surface plasmon wave wavelength is as follows：

由公式(2)可知，表面等离激元波的波长为：

(3)

where，λ0is incident wavelength.

式中，λ0为入射光波长。

SPP波有3个特征长度，分析如下。

Three characteristic lengths of SPP wave are analyzed as follows.

(4)

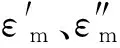
(5)

(6)

Where,k0is the incident light wave vector[12]. From equation (4) to (6), the distance of light in 550-700 nm waveband propagating on the silver surface is in the range of 12.5-60 μm, the penetration depth of SPP in air and silver is in the range of 279-500 nm and 22.7-29.5 nm, respectively.

式中，k0为入射光的波矢量[12]。由式(4)～(6)可得，550～700 nm波长的光波在金属银表面的传播距离为12.5～60 μm时，SPP在空气和银中的穿透深度分别为279～500 nm和22.7～29.5 nm。

3 Determination of optimal structure of metallic grating coupler

最优激发金属光栅结构的确定

Fig.2 shows the model for studying the near-field diffraction of SPP waves.The left metal grating is used to as grating coupler to excite the SPP wave, the right metal grating serves as the diffraction grating. When light is incident on the metal grating structure, an SPP wave is generated on the metal surface and propagates to both left and right along the metal surface. Near-field diffraction occurs when a diffraction grating is encountered.

图2是研究SPP波超表面近场衍射的模型。左侧是激发SPP波的金属光栅结构，右侧是衍射光栅。当光入射到金属光栅结构上时，会在金属表面产生SPP波，产生的SPP波将沿着金属表面向右传播，遇到衍射光栅时便会发生近场衍射现象。

In this paper, the near-field diffraction of SPP waves excited by incident light with wavelength in the range of 550-700 nm and the central wavelength of 625 nm is studied. The coupling efficiency of incident light to SPP wave is mainly related to the structure parameters of metal grating coupler such as cycle, filling factor and modulation depth. The material of the metal grating coupler is set as silver, and it can be seen from equation (2) that for the incident light with a wavelength of 625 nm, the coupling efficiency of the incident light is the highest when the grating periodΛis 607 nm. The grating filling factorDis set to 0.5 and the grating depthhis 200 nm. By emplaying the rigorous coupled wave theory, the reflectivity of the incident light against the wavelength ranging from 550-700 nm, and the incident angle ranging from 10-15° was calculated by using the SPR angle scanning method[13]. Fig.3(a) shows the three-dimensional map of the reflectivity and against the wavelength and the angle of incidence. Fig.3(b) illustrates the relationship of the reflectivity and wavelength for different incident angles.

本文主要研究中心波长为625 nm，波段为550～700 nm的入射光激发的SPP波近场衍射现象。而入射光耦合激发SPP波的效率主要与金属光栅的面型参数如周期、占空比及调制深度等有关。设定耦合金属光栅的材料为银，通过式(2)可知，对于波长为625 nm的入射光，光栅周期Λ为607 nm时，入射光的耦合率最高。光栅占空比D设为0.5，光栅厚度h设为200 nm。根据严格耦合波理论，利用SPR角度扫描方法[13]，计算入射光波长为550～700 nm、入射角在10°～ 15°范围内入射光的反射率，得到反射率与波长及入射角度的三维关系图，如图3(a)所示。图3(b)为反射率与波长及入射角的关系曲线图。

It can be seen from Fig.3(a) that for the above mentioned metal grating structure, the reflectivity is lower for 625 nm wavelength when incident angle falls on the range of 12.5°-15°. It can be further deduced from Fig.3(b) that when the incident angle is about 14°, the reflectivity is the mimimum, that means the coupling efficiency is the highest, about 35%. At this incident angle, the coupling ratio is 25% and 10% for 550 nm and 700 nm respectively.

由图3(a)可以看出，在上述金属光栅结构下，波长为625 nm的光以12.5°～15°入射时，反射率较低。由图3(b)进一步可得，当入射角约等于14°时，反射率最小，即耦合成SPP波的效率最高，大约在35%左右。在此入射角下，550 nm波长的入射光的耦合率为25%，700 nm波长的入射光的耦合率在10%左右。

4 Diffraction results and analysis

衍射结果与分析

When the period of the metal silver grating is 607 nm, the wavelength of SPP waves excited by the incident light with a wavelength ranging from 550-700 nm is in the range of 525 to 683 nm. As shown in Fig.2, the metal grating coupler has a period of 607 nm, filling factor of 0.5 and a groove depth of 200 nm. The right diffractive metal grating located on the metal surface has a height of 600 nm and a thickness of 200 nm in theXdirection. When studying the diffractive behavior of SPP waves through a metal grating, two cases are considered:one is the case where the grating height and filling factor keep no change but the grating period changes; the other case is that the grating height and period keep no change but the filling factor changes. At the same time, the excitation wavelength and the incident angle are fixed at 625 nm and 14°.

当金属银的光栅周期为607 nm时，波长为550～700nm的入射光激发出的SPP波波长在525～683 nm之间。设定图2所示的近场衍射模型中激发SPP波的金属光栅周期为607 nm，占空比为0.5，凹槽深度为200 nm。右方衍射金属光栅位于金属表面上，高度为600 nm，在X方向上的厚度为200 nm。当研究SPP波经过其的衍射行为时，对以下两种情况分别研究：一种是光栅高度和占空比不变，而光栅周期发生变化时的情况；另一种是光栅高度和周期不变，占空比发生改变的情况。同时激发光波长和入射角度固定为625 nm和14°。

4.1 Diffraction situation by fixed diffraction grating filling factor but different period

衍射光栅占空比固定,周期不同时的衍射情况

Figs.4(a)-4(e) show the near-field diffraction of the SPP wave excited by the incident light with the wavelength of 625 nm when the filling factor of the diffraction grating is constant(0.5) and the period is different. In the figures,XYplane is the metal film surface, and the diffraction grating is located on theY-axis.

图4(a)～4(e)是波长为625 nm的入射光所激发的SPP波在衍射光栅占空比一定(0.5)而周期不同时的近场衍射现象。图中XY平面为金属薄膜表面，衍射光栅位于Y轴上。

Fig.4 Diffraction phenomenon of SPP wave of incidence light with wavelength of 625 nm when diffraction grating with different period but the same filling factor(It should be noted that the white dashed line represents the location of the diffraction grating) 图4 波长λ=625 nm的入射光激发的SPP波在周期不同，占空比一定的条件下的衍射现象(图中白色断线表示金属衍射光栅的位置)

It can be seen that there is only the 0th diffraction order at this time. The transmitted light intensity is quite weak, below 0.2, and the transmission distance is only about 2.3 μm after passing through the diffraction grating; Fig.4(b) is the case when the period of the diffraction grating isλspp. In this case, the diffraction phenomenon can be observed and one can see that besides the 0th order, ±1 storders are also appear. The light intensity at this time also increases significantly with the maximum reaches to about 1, while the transmission distance also increases to about 4 μm; Figs.4(c)-(e) depict the diffraction of the SPP wave when the diffraction grating period is 1.5λspp, 4λsppand 6λspp, respectively. It can be seen that the diffraction order increases correspondingly as the period of the diffraction grating increases. When the diffraction grating period is 1.5 times of the SPP wavelength, the highest order of the diffraction is ±2nd and the distinction of diffraction fringes is relatively clear. When the grating period is 4-6 times of the SPP wavelength, the distribution of diffraction fringes becomes more disordered due to even higher diffraction orders appear.

图4(a)为当衍射光栅周期为0.5λspp时SPP波的衍射情况。可以看到此时只有零级衍射，且透射光强较弱，在0.2 μm以下，入射光透过衍射光栅后传播距离在2.3 μm左右；图4(b)为衍射光栅周期为λspp的情形，此时已有明显的衍射现象，可以看到0级和±1级衍射，并且此时光强有明显的增强，最大达到了1左右，同时透过衍射光栅后SPP光的传播距离在4 μm左右；图4(c)～4(e)为衍射光栅周期分别为1.5λspp、4λspp和6λspp时SPP波的衍射情形。可以看到，随着衍射光栅的周期不断增大，衍射级次相应地增多。当衍射光栅周期为SPP波长的1.5倍时，最高衍射级次为±2级，并且衍射条纹的分布比较清晰；而当光栅周期为SPP波长的4～6倍时，由于更高衍射级次的出现使得衍射条纹的分布变得较为紊乱。

4.2 Diffraction behavior of diffraction grating with fixed period but different filling factor

衍射光栅周期固定,占空比不同时的衍射情况

Figs.5(a)-5(e) show the near-field diffraction of the SPP wave at the metaface with a constant period of the diffraction grating of 910 nm, but the filling factor changes. In the Fig.5, theXYplane is the metal film surface, and the diffraction grating is located on theY-axis. Fig.5(f) illustates the electric field intensity distribution corresponding to the Fig.5(a)-5(d) near field diffraction on the surface of the metal thin film atx=0.

Fig.5 Diffraction phenomenon of SPP wave for an incidence light with wavelength of 625 nm for diffraction grating with different duty ratios and the fixed grating period. (a)Duty radio is 0.1; (b)Duty radio is 0.3； (c)Duty radio is 0.5; (d)Duty radio is 0.7; (e)Duty radio is 0.9; (f)Electric field intensity distribution of the diffraction patterns along y axis under different duty radio at x=0 图5 入射光波长λ=625 nm,衍射光栅周期为910 nm，占空比不同时的衍射现象，其中白色虚线表示金属光栅的位置。(a)占空比为0.1；(b)占空比为0.3；(c)占空比为0.5；(d)占空比为0.7；(e)占空比为0.9；(f)衍射光栅占空比不同时，金属薄膜表面上x=0直线上的近场衍射电场强度曲线图

图5(a)～5(e)为衍射光栅周期固定为910 nm不变，占空比变化时SPP波在超表面的近场衍射情形。图中XY平面为金属薄膜表面，且衍射光栅位于Y轴上。 图5(f)为对应于5(a)～5(d)金属薄膜表面直线x=0上近场衍射的电场强度分布图。

As can be seen from the graphs in Figs.5(a)-(e), the SPP wave finally converges on the metal surface after passing through the diffraction grating, and the diffraction order does not change substantially, but the intensity changes as the filling factor of the diffraction grating changes. When the filling factor of the grating changes from 0.1 to 0.7, the diameter of the converging light beam gradually becomes smaller. When the grating filling factor is 0.9, the light transmittance has become very low, so that the maximum electric field intensity is only about 0.3. It can be seen from Fig.5(f) that the diffraction angle the SPP wave in of near-field also varies when the filling factor of grating is different. The diffraction angle of the ±1 storderis in the range of 39.79° to 42.67° for different filling factors. When the filling factor is 0.1, the diffraction angle is the smallest, i.e. 39.79°. The diffraction angle is the largest at 42.67° when the filling factor is 0.5. The diffraction angle is very close, i.e. about 41°, when the filling factor ranges from 0.3 to 0.7. The light field intensity of ±1 diffraction order varies with different filling factor, which is related to the different intensity of the SPP wave passing through the diffraction grating.

从图5(a)～5(e)可以看到，SPP波透过衍射光栅后,在金属表面上最终都汇聚到一起,衍射级次基本不发生变化，但强度随着衍射光栅占空比的变化而变化。当光栅占空比从0.1变化到0.7时,汇聚光束的直径逐渐变小。当光栅占空比为0.9时,光的透过率已经变得非常低，电场强度最大只有0.3左右。从图5(f)中可以看出，光栅占空比不同时，SPP波的近场衍射角也有所变化，几种不同占空比的衍射光栅对应的±1级衍射角在39.79°～42.67°内,其中:当占空比为0.1时,衍射角最小,为39.79°;占空比为0.5时,衍射角最大,为42.67°;占空比为0.3或0.7时,衍射角接近,在41°左右。占空比不同,±1级的光场强度也不同,这也与SPP波透过衍射光栅的光强不同有关。

4.3 Comparison of diffraction behaviors of metal gratings in free space and on meta-surface

自由空间中与超表面上金属光栅衍射行为比较分析

To further illustrate the difference between the grating diffraction behavior of SPP waves on the meta-surface and that in free-space light, we also calculated the diffraction effect of metal gratings in free space and compared them with those on the meta-surface. Fig.6(a) shows the free space grating diffraction model. Here for the convenience of comparison, let the incident light wavelength and SPP wavelength to be 607 nm as well, and let the thickness of the metal grating also equal to 200 nm. However, the difference is that the height of the metal grating on the meta-surface is limited to 600 nm in the direction perpendicular to the period, while the size of the metal grating in the free space in the direction perpendicular to the period is infinitely large.

Fig.6 Comparison of near field diffraction of SPP wave and free space light: (a)theoretical model for near field diffraction of free space light; (b)near field diffraction of SPP on meta-surface; (c)near field diffraction in free space light; (d)electric field distribution in X direction at 0.95 μm from diffraction grating corresponding to (b); (e)electric field distribution in Z direction at 0.95 μm corresponding to (c); (f)electric field intensity at the surface of the metal film corresponding to (d), (e) 图6 自由空间光与超表面上光栅近场衍射行为对比结果图：(a)空间光的近场衍射装置图；(b)SPP波超表面上的光栅近场衍射图；(c)自由空间光的光栅近场衍射图；(d)对应(b)在距衍射光栅0.95 μm处X方向上的电场分布图；(e)对应(c)在距衍射光栅0.95 μm处Z方向上的电场分布图；(f)对应(d)、(e)在金属薄膜表面处的电场强度曲线

为进一步说明超表面上SPP波的光栅衍射行为和自由空间光的光栅衍射行为的区别。本文对自由空间中金属光栅进行了计算，并和超表面上的情况进行比较。图6(a)所示为自由空间光栅的衍射模型图。这里为方便比较，使入射光波长和SPP波波长相等，都为607 nm，并且金属光栅厚度相等，皆为200 nm，但不同之处在于超表面上金属光栅在和周期垂直方向上高度有限制，为600 nm，而自由空间中的金属光栅在和周期垂直方向上的尺寸取无限大。

Fig.6(b) shows the grating near-field diffraction of the SPP wave for an incident wavelength of 625 nm. The wavelength of the SPP wave excited at this time is 607 nm and the period of the diffraction grating is 910 nm, which is about 1.5λspp, the filling factor is 0.5. Fig.6(c) shows the near-field diffraction of the space light with an incident wavelength of 607 nm. In order to compare the diffraction phenomenon on the metasurface to that in free space, the period, filling factor and thickness of the diffraction grating is set to 910 nm、 0.5 and 200 nm respectively.

图6(b)是入射光波长为625 nm时激发的SPP波在超表面上的光栅近场衍射情形，此时激发的SPP波波长为607 nm，衍射光栅周期设为910 nm，约为1.5λspp，占空比为0.5。图6(c)为入射光波长为607 nm的空间光的近场衍射情形。为了对比分析空间光与SPP波在超表面的衍射现象，设衍射光栅周期为910 nm，占空比为0.5，金属光栅厚度为200 nm。

Comparing Fig.6(b) and 6(c), one can see that the diffractive behavior of SPP wave is similar to the phenomenon when space light is diffracted in the near field. Fig.6(d) and 6(e) correspond to the electric field intensity plots forZ>0(i.e SPP waves in air) atX=0.95 μm in Fig.6(b) and 6(c). The SPP wave exponentially decays in the medium and in the metal, so that on the metal film surface, the electric field intensity reaches its maximum value and decays rapidly in theZdirection. Where as space light propagates uniformly in the medium[14], the intensity of the electric field in theZ-direction is uniformly distributed. Fig.6(c) is light intensity distribution curve on the metal surface corresponds to Fig.6(d) and 6(e). As can be seen from the figure, in addition to the difference in field intensity, the position of 0th and ±1th diffraction orders are basically the same.

比较图6(b)和6(c)可以看出，SPP波与空间光在近场衍射现象类似。图6(d)和6(e)为对应图6(b)、6(c)中X=0.95 μm处，Z>0部分(即SPP波在空气中)的电场强度图，SPP波在介质和金属中光强呈指数衰减，因此在金属薄膜表面上，电场强度取得最大值，在Z轴方向迅速衰减。而空间光在介质中是均匀传播的[14]，所以在Z轴方向电场强度是均匀分布的。图6(c)对应图6(d)、6(e)在金属表面上光强分布曲线图，从图中可以看出，二者除了在强度上有所区别外，0、±1衍射级的位置基本一致。

In addition, it is clear that the near-field diffraction angles of the SPP waves excited by different incident wavelengths on the meta-surface are also different after diffraction by metal grating on metasurface. It is known from equation (3), when the incident light wavelengths is 550 nm, 581 nm, 616 nm, 655 nm and 700 nm respectively, the wavelength of SPP waves excited by the device in Fig.2 is 524.7 nm, 557.9 nm, 594.8 nm, 635.8 nm and 682.9 nm, and the ±1 order near-field diffraction angles after metal grating diffraction on the metasurface is 35.737°, 36.966°, 38.157°, 39.311° and 41.507°, respectively. For diffraction of light in free space, when light with a wavelengths of 524.7 nm, 557.9 nm, 594.8 nm, 635.8 nm and 682.9 nm respectively is incident on the diffraction grating with the same structural parameters as shown in Fig.6(a), the resulting far-field diffraction angle can be determined by:

此外，很显然超表面上不同入射波长所激发的SPP波经光栅衍射后的近场衍射角也不同，由式(3)可知，当入射光波长分别为550、581、616、655及700 nm时，利用图2的装置激发出的SPP波波长依次为524.7、557.9、594.8、635.8及682.9 nm，且经过超表面上金属光栅衍射后的±1级的近场衍射角分别为35.737°、36.966°、38.157°、39.311°及41.507°。而对于自由空间中光的衍射，将波长分别为524.7、557.9、594.8、635.8及682.9 nm的光入射到图6(a)所示具有相同结构参数的衍射光栅上时产生的远场衍射角可由下面式(7)决定：

dsinθ=kλ.

(7)

By using this formula, the corresponding diffraction angles are determined to be 31.653°, 33.916°, 36.503°, 39.485° and 43.071° respectively. In comparison with the case on meta-surface, it can be found that the near-field diffraction angle is almost the same, and the maximum error is only about 5°. This means that the diffraction angle of the SPP wave after transmitted through the metal grating on the meta-surface can be roughly estimated by using the conventional grating diffraction formula in free-space-of, but more accurate results have to be obtained by rigorous numerical calculations.

利用该公式可计算得出所对应的衍射角分别为31.653°、33.916°、36.503°、39.485°及43.071°。两相对比，可发现其与SPP波透过衍射光栅后的近场衍射角相差不大，最大误差仅约5°。这说明，采用常规的用于自由空间光光栅衍射公式，可以对超表面上光栅的衍射角度进行粗略估计，但更准确的结果必须通过严格数值计算来获得。

4.4 Comparison of diffraction of two kinds of diffraction gratings on metasurface

超表面上两种衍射光栅衍射情况的对比

Figs.7(a) and 7(b) show two kinds of diffraction gratings on the meta-surface, Fig.7(a) shows the case where the diffraction grating protrudes on the metal surface; and Fig.7(b) shows the case where the diffraction grating is recessed on the metal surface. In Fig.7(a), in order to avoid the influence of stray light on the diffraction of near-field SPP wave, the height of the diffraction grating is set to be 600 nm, which is equal to the penetration depth of the SPP wave in the air and the width is 200 nm. In order to compare the near-field diffraction of the two kinds of diffraction gratings, the depth of the diffraction grating grooves in Fig.7(b) is set to be 600 nm and the width is set to be 200 nm which is the same as that in Fig.7(a). The two kinds of diffraction gratings are set to have the same period and filling factor.

图7(a)、7(b)为超表面上两种衍射光栅示意图，图7(a)为衍射光栅凸起于金属表面的情形；图7(b)为衍射光栅凹进金属表面的情形。图7(a)中，为了避免杂散光对SPP波近场衍射的影响，设衍射光栅的高度为600 nm，与SPP波在空气中的穿透深度相等，宽度为200nm。为对比两种衍射光栅的近场衍射情况，取图7(b)中衍射光栅凹槽深度为600 nm，宽度为200 nm，与图7(a)相同，且设定两种衍射光栅的周期和占空比均相同。

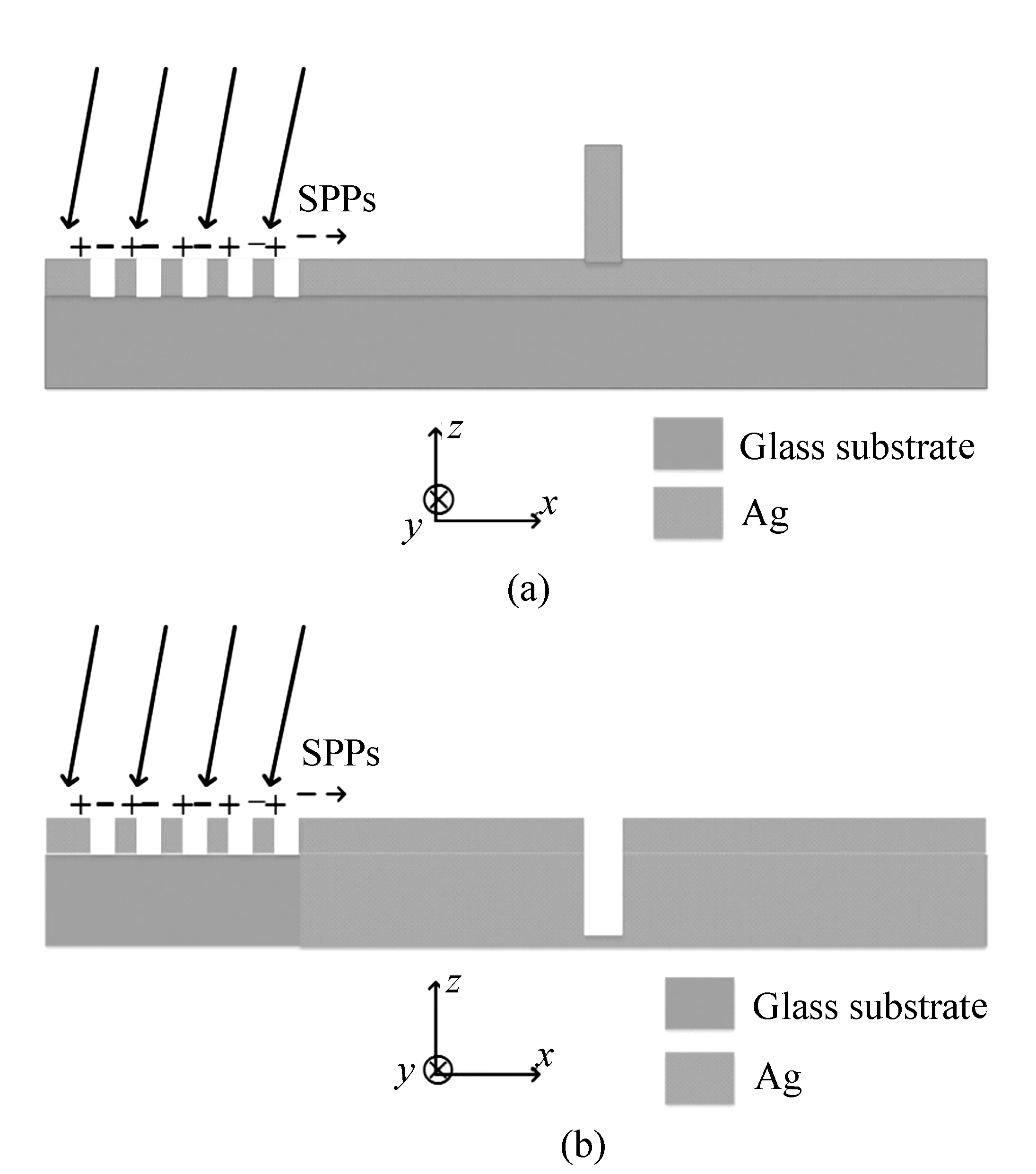
Fig.7 Schematic diagrams of two kinds of diffraction gratings 图7 两种衍射光栅的示意图

The grating period, the filling factor and depth of grating coupler of excitation SPP wave on the left of the above two structures is set to be 607 nm, 0.5, 200 nm respectively, the incident light wavelength is in the range of 550-700 nm and the incident angle is 14°. Figs.8(a) and 8(b) show the near-field diffraction of SPP waves under the above mentioned two grating structures, respectively. In Fig.8,XYplane is the metal film surface, the diffraction grating is located on theY-axis.

设定上述两种结构左侧激发SPP波的光栅周期为607 nm，占空比为0.5，光栅深度为200 nm，入射光波长为550～700 nm，入射角度为14°。图8(a)、8(b)分别为在上述两种光栅结构下，SPP波的近场衍射情况。图中XY平面为金属薄膜表面，衍射光栅位于Y轴上。

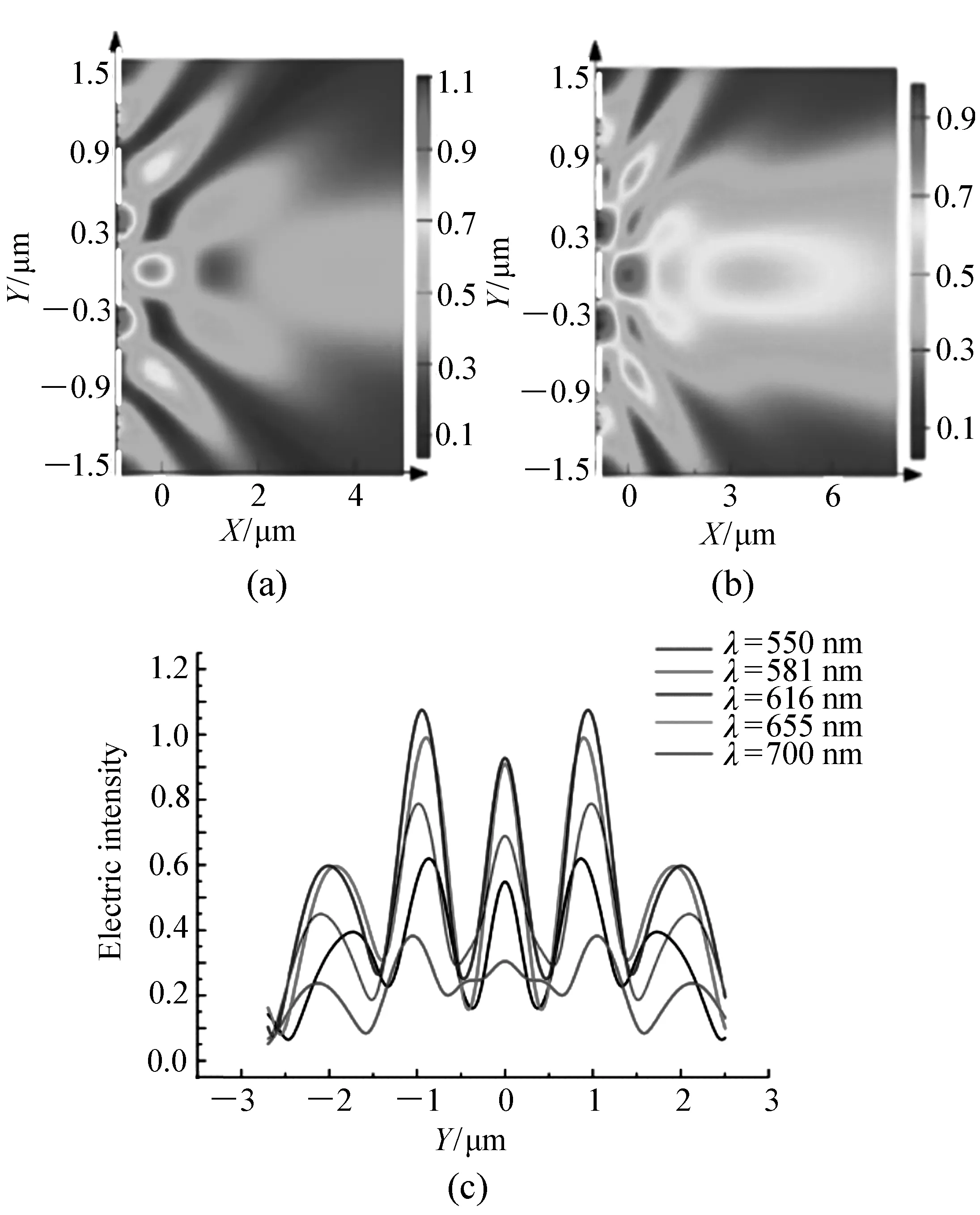
Fig.8 (a)Near field diffraction of the incident light at 625 nm Corresponding to Fig.7(a); (b)near field diffraction of the incident light at 625 nm Corresponding to Fig.7(b); (c)curve of near field diffraction of the incident light at 550-700 nm corresponding to Fig.7(b). White dashed line in the figure(ieft sode) represents the grating location 图8 (a)对应图7(a)所示结构，入射波长为625 nm的近场衍射；(b)对应图7(b)所示结构，波长625 nm时近场衍射；(c)对应图7(b)所示结构，入射光波长为550～700 nm的近场衍射曲线图。图中左侧白色虚线表示衍射光栅所在位置

Fig.8(c) shows the near-field diffraction curve with an incident light wavelength of 550-700 nm corresponding to the structure shown in Fig.7(b). As can be seen from the figure, the zero-th diffraction order of each wavelength center is located aty=0, but for diffraction orders of ±1, ±2, there have been obvious diffractive effect. The reason is that the intensity of the electric field diffracted by the SPP wave is different that for the fixed metal grating coupling structure there is only one optimal incident wavelength, and at this wavelength, the light is coupled into the SPP wave most efficiently[15].

图8(c)为对应图7(b)所示结构，入射光波长为550～700 nm的近场衍射曲线图。从图中可以看出，各波长的零级衍射的中心均在y=0上，但在±1、±2衍射级时已经有明显的分光现象。不同波长的入射光所激发的SPP波衍射后的电场强度不同，原因是，固定的金属光栅耦合结构只对应一个最佳的入射波长，这个波长的光耦合成SPP波的效率最高[15]。

In Fig.8(d), the incident light of 550-581 nm is separated by 1.23°and the incident light of 581-616 nm is separated by 1.20°on the metal surface. The incident light of 616-655 nm is separated by 1.15° and the incident light at 655-700 nm is separated by 2.20° on the metal surface due to the near-field diffraction of the SPP wave. Since the excitation and propagation of SPP waves in near-field diffraction are on the order of micrometers[15], the signal of incident light can be separated by the near-field diffraction of SPP wave to realize micron-scale spectrometer.

图8(d)中由于SPP波的近场衍射， 550～581 nm的入射光在金属表面上分开1.23°，581～ 616 nm的入射光在金属表面上分开1.20°，616～655 nm的入射光在金属表面上分开1.15°，655～700 nm的入射光在金属表面上分开2.20°。在近场衍射中由于SPP波的激发和传播都在微米量级[15]，可以利用SPP波的近场衍射现象对入射光的信号进行分离,制备微米量级的光谱仪器。

5 Conclusions

结 论

In this paper, the near-field diffraction of SPP waves excited by visible light incident on metal grating structures in the wavelength range of 550-700 nm is studied by a method of metal grating coupling. First of all, according to the rigorous coupling wave theory, the SPR angle scanning method is used to find the optimal metal grating structure with the highest coupling efficiency for the incident light with the central wavelength of 625 nm. Then the effect of metal grating structure parameters on the near-field diffraction of SPP wave is studied. The results show that the diffraction effect of SPP is most pronounced when the period of the diffraction grating is 1.5 times the wavelength of SPP and the filling factor is 0.5. Finally, using the phenomenon of SPP wave near-field diffraction, the incident light of 550-558 nm can be separated by 1.23° on the metal surface, the incident light of 581-616 nm is separated by 1.20° on the metal surface and the incident light of 616-655 nm can be separated by 1.15° on the metal surface, the 655-700 nm incident light can be separated by 2.20° on the metal surface. Finally, the diffraction of SPP wave and the diffraction of free space light are compared. We discover that the diffraction angle calculated from the free-space grating diffraction formula is similar to that of the SPP wave. The formula can be used to make a rough estimate of the diffraction angle of a grating on a meta-surface.

本文利用金属光栅耦合方式,对波长在550～700 nm范围内的可见光入射到金属光栅结构上激发的SPP波的近场衍射现象进行了研究。首先根据严格耦合波理论，利用SPR角度扫描方法，找出中心波长625 nm的入射光耦合效率最高的金属光栅结构。然后研究了金属光栅结构参数对SPP波近场衍射的影响。结果表明，当衍射光栅的周期为SPP波波长的1.5倍、占空比为0.5时，SPP波的衍射效果最明显。最后，利用SPP波的近场衍射现象，可将550～581 nm的入射光在金属表面上分开1.23°，581～616 nm 的入射光在金属表面上分开1.20°，616～655 nm的入射光在金属表面上分开1.15°，可将655～700 nm的入射光在金属表面上分开2.20°。最后将SPP波的衍射情况和自由空间光的衍射情况进行比较，发现根据自由空间光栅衍射公式计算出的衍射角度和SPP波的情况相差不大，可以用该公式对超表面上光栅的衍射角度进行粗略估算。

[1] 梁秋群.金属纳米结构表面等离激元杂化和吸收特性的研究[D].北京：中国科学院大学，2015.

LIANG Q Q. Study on plasmon hybridization and optical absorption properties of metallic mano-structures[D]. Beijing:University of the Chinese Academy of Sciences,2015.(in Chinese)

[2] 曹水艳.表面等离子体结构聚焦和吸收特性的研究[D].北京：中国科学院大学,2013.

CAO SH Y. Study on the property of focusing and absorption of plasmonic nanostructures[D]. Beijing：University of the Chinese Academy of Sciences,2013.(in Chinese)

[3] LIU N,MESCH M,WEISS T,etal.. Infrared perfect absorber and its application as plasmonic sensor[J].NanoLett.,2010,10(7):2342-2348.

[4] DREGELY D,TAUBERT R,GIESSEN H,etal.. 3D optical Yagi-Uda nanoantenna array[J].Nat.Commun.,2011,2:267.

[5] CAI W,SHALAE V V. Optical metamaterials:fundamentals and applications[J].ContemporaryPhysics,2012,53(3):278-279.

[6] YANG J Z,WANG T S,CHEN Z L,etal.. Super-resolution imaging at mid-infrared waveband in graphene-nanocavity formed on meta-surface[J].ScientificReports,2016,6:37898.

[7] 肖钰斐,张卫平,黄海华,等.金属光栅结构对表面等离子体共振的影响[J].中国激光,2013,40(11):245-250.

XIAO Y F,ZHANG W P,HUANG H H,etal.. Influence of function of metal grating shape on surface plasmon resonance[J].ChineseJ.Laser,2013,40(11):245-250.(in Chinese)

[8] 刘媛媛，熊广，王杨，等.多谐振斦形缝隙纳米天线设计及吸收特性[J].光学 精密工程，2017，25(8):2155-2164.

LIU Y Y,XIONG G,WANG Y,etal.. Design of multi resonant U shaped slots nano-antenna and their absorption properties[J].Opt.PrecisionEng.,2017，25(8):2155-2164.(in Chinese)

[9] 陈烽,叶雄英,伍康,等.双波长集成光栅干涉微位移测量方法[J].光学 精密工程，2012，20(11):2433-2438.

CHEN F，YE X Y，WU K，etal.. Displacement measurement method based on integrated grating interferometry with two-wavelength lasers[J].Opt.PrecisionEng.，2012，20(11):2433-2438.(in Chinese)

[10] ZHANG X,LIU Z. Superlenses to overcome the diffraction limit[J].Nat.Mater.,2008,7:435-441.

[11] 胡昌奎.基于纳米金属光栅结构的表面等离子体共振传感研究[D].武汉：华中科技大学,2010.

HU CH K. Study on surface plasmon resonance sensor basde on nano metallic surface-relief grating[D]. Wuhan:Huazhong University of Science & Technology,2010.(in Chinese)

[12] 张善文，巴音贺希格.宽波段金属光栅设计中闪耀波长对光栅异常的补偿效应[J].光学 精密工程，2009，17(5):990-1000.

ZHANG SH W,BAYINHESHIG. Compensating effect of blazed wavelength to grating anomalies in design of broadband metallic diffraction gratings[J].Opt.PrecisionEng., 2009，17(5):990-1000.(in Chinese)

[13] RAETHER H.SurfacePlasmonsonSmoothandRoughSurfacesandonGratings[M]. Springer-Verlag Berlin Heidelberg,1988.

[14] 石顺祥,刘继芳,孙艳玲.光的电磁理论:光波的传播与控制[M].西安：西安电子科技大学出版社,2006.

SHI SH X,LIU J F,SUN Y L.ElectromagneticTheoryofLight:PropagationandControlofLight[M]. Xi′an：University of Xi′an Electronic Science and Technology Press,2006.(in Chinese)

[15] GAZZPLA E,BRIGO L,ZACCO G,etal.. Coupled SPP modes on 1D plasmonic gratings in conical mounting[J].Plasmonics,2014,9(4):867-876.