时间传播网络中受影响顶点的预测
林天巧,赵 雷
(苏州大学 计算机科学与技术学院,江苏 苏州 215006)
0 概述
受影响顶点预测是信息传播研究的一个基本问题,在广告推荐、流行病预测和社交网络的信息传播等研究中都有广泛的应用。对于广告商而言,在广告发布后需要获知被该广告影响的用户,从而进行广告评估,制定营销策略。在流行性疾病和计算机病毒传播中,需要快速确认并处理感染者,从而控制病毒传播。但由于信息传播具有随机性和不确定性,有效预测出受影响者较为困难,因此本文将受影响顶点预测与顶点状态验证相结合来预测发现受影响顶点,从而确定信息的扩散范围。但顶点状态验证需要对顶点的属性进行分析,这会耗费大量计算资源,且在许多应用中允许的验证次数往往是有限的。
本文研究时间传播网络(Temporal Diffusion Network,TDN)中受影响顶点的预测问题。首先给出受影响顶点预测问题的形式化定义,然后设计基于顶点受影响概率的启发式预测算法IPH,并在此基础上,结合广度优先遍历(Breath First Search,BFS)顶点选择策略进一步提出相邻顶点受影响概率启发式预测算法AIPH,最后在模拟数据集和真实数据集上进行实验。
1 研究现状
影响是通过接触而发生和传播的,如社交网络中信息的发布和对信息的评论、回复、转发等就属于一种影响的发生和传播。当接触具有明显的时间特征如随时间改变、存在时间间隔等时,接触可被抽象为时间图[1]中的信息传播,即TDN,研究者据此研究受影响顶点预测问题。通过用户行为分析[2]、传播概率推测[3]和传播网络推测[4-6]等方法,能够预测时间传播网络中各边的传播概率。
图1是一个TDN的示例,图中的边表示接触,如边(A,B,1,2)为A在时间1与B之间延迟为2的一次接触,P1~P18为预测得到的边上的传播概率。由于信息安全与用户隐私保护等原因,在TDN中只记录用户之间的接触并不记录具体传播内容。

图1 TDN示例
目前关于受影响顶点预测问题的研究工作主要分为遍历抽样方法和机器学习预测方法。遍历抽样方法(如随机游走[7-8]和BFS[8-9]等)依据网络结构进行顶点选择,但未利用信息传播知识,不能有效地预测发现受影响顶点;机器学习预测方法[5,10-11]利用逻辑回归算法等在传播网络中根据历史传播数据预测顶点影响力和信息的最终扩散范围,但学习复杂度较高不能用于大图,并且容易出现过拟合现象。上述方法可以用于解决一部分具有代表性的图中信息传播的影响预测问题,如影响力最大化问题[9-15],但TDN中受影响顶点的预测问题仍然存在以下难点:
1)受影响顶点预测并非影响力最大化问题。在受影响顶点预测和部分影响力最大化问题中,虽然都涉及顶点受影响概率计算,但影响力最大化问题是利用顶点受影响概率计算得到顶点影响力后需要解决的顶点组合最优问题,而受影响顶点预测则是利用顶点受影响概率计算受影响顶点到其他顶点的联合概率,且在顶点状态验证后需要迭代更新候选集合中顶点的受影响概率。因此,影响力最大化问题研究成果只能部分应用于受影响顶点预测中。
2)TDN中受影响顶点预测必须满足图中信息传播的时间约束,即顶点在获得信息后才能向其他顶点传播信息。因此,预测顶点间能否产生影响并非通过简单的连通性计算就能完成。
3)在静态传播网络中准确计算顶点受影响概率是#P-hard问题[9],在TDN中该问题仍然是#P-hard问题。由于TDN(如社交网络)通常具有顶点用户数量大、信息更新速度快等特性,因此现有算法难以有效预测出受影响顶点。
受影响顶点预测是信息传播中有广泛应用场景的基本问题,如广告评估、疾病传播控制、舆论分析等都涉及受影响顶点的预测发现。传播概率推测[3]、传播网络推测[4-6]、影响力最大化问题[9-15]、传播模型研究[3,5,10,16-19]等研究成果可用于信息传播预测的研究。IC模型和LT模型是信息传播预测中最主要的2个预测模型[14-15]。由于信息传播随时间改变,GOMEZ等人基于IC模型提出了NETINF[3]、NETRATE[5]和INFOPATH[17]模型来推测传播网络以及边上传播概率。随着时间图[1]研究的推进,对于时间图上路径问题[20]的研究也不断出现。基于上述成果,本文在时间传播网络中研究受影响顶点预测问题。
影响力最大化问题[9-15]是信息传播预测研究中的热点问题,该问题的求解目标是:对于给定顶点数k,从传播网络中求得使预期受影响顶点最多的k个顶点组合。该问题由顶点影响力评估和顶点组合最优2个问题组成,这2个问题都是NP-hard问题,其中顶点组合最优问题是影响力最大化问题的核心。文献[9]通过MIA模型进行顶点选择,在计算顶点影响力时基于MIA模型使用最大传播路径MIP近似计算顶点影响力。文献[11]则不使用传播模型直接学习顶点影响力,并利用梯度下降法进行顶点选择。虽然在受影响顶点预测和一些影响力最大化问题研究中都涉及计算顶点受影响概率,但这2个问题存在明显差异:在影响力最大化问题中,顶点影响力用顶点期望受影响顶点数表示,而受影响顶点预测需要计算受影响顶点到待计算顶点的联合概率,并且受影响顶点预测在顶点验证后需要更新候选集,而影响力最大化问题则需要解决顶点组合最优问题。因此,影响力最大化问题的研究成果可以部分应用于受影响顶点预测中,但并不完全适用。
本文对受影响顶点预测问题研究的目标是在有限的k次验证中尽量多地发现受影响顶点,主要工作如下:
1)根据文献[21]在静态传播网络中提出的Inclusion-Exclusion影响力计算方法,提出基于IC模型[15]的TDN顶点受影响概率计算方法与跳数受限近似(Hop Limited Approximative,HLA)计算方法。
2)根据HLA方法提出基于顶点受影响概率的受影响概率启发式预测算法IPH,用以预测TDN中信息传播的受影响顶点。同时利用提出的IPC算法构造可达顶点构成的候选集合,并使用CSU候选集更新算法来更新顶点状态验证后的候选集合。
3)IPH算法虽然能够在验证次数较少时有效预测发现受影响顶点,但当验证次数k较大时,该方法准确率将较低。为解决该问题,本文结合BFS算法顶点选择策略,在IPH算法基础上提出相邻顶点受影响概率启发式预测算法AIPH。
由于信息传播的随机性,抽样与图遍历算法相对于机器学习方法[13]更适用于受影响顶点预测。文献[7]比较了若干抽样算法的性能,并发现随机游走(Randow Walk,RW)算法和Forest Fire算法的效果最好。信息传播存在广度传播特征,BFS相对其他遍历算法更能有效预测发现受影响顶点。因此,本文在TDN中预测受影响顶点时,将BFS算法和随机游走算法作为实验对比算法。
2 相关定义
2.1 时间传播网络
信息通过接触而发生传播,但接触随时间改变且存在时间间隔,因此,本文将接触构成的传播网络定义为时间传播网络(TDN),TDN中每一条边代表一次接触。
定义1(时间传播网络) 时间传播网络G={V,E},V是顶点集合,E是边集。边e=(u,v,t,d)∈E表示顶点u通过时间t时开始延迟为d的边e向顶点v传播信息。边上传播概率ξ(e)为u通过边e对v影响的概率,0<ξ(e)<1。到达时间Tv=t+d为v的接收时间,顶点v在Tv之后才能向其他顶点传递信息。
由于信息传播是有向的,因此时间传播网络G为有向图。在TDN中顶点间可能存在重边,如图1中边(A,C,2,1)和(A,C,2,3),这表示一个顶点多次向另一顶点传播信息。通过用户行为分析[2]、传播概率推测[3]和传播网络推测[4-6]能够推测出TDN中各边的信息传播概率,因此,本文在受影响顶点预测时将边上传播概率ξ(e)作为已知参数进行计算。
信息在TDN中传播需要满足时间约束条件:顶点在获得信息后才能向其他顶点传播信息,因此,TDN中信息传播的路径为满足时间约束条件的时间传播路径,其定义如下:
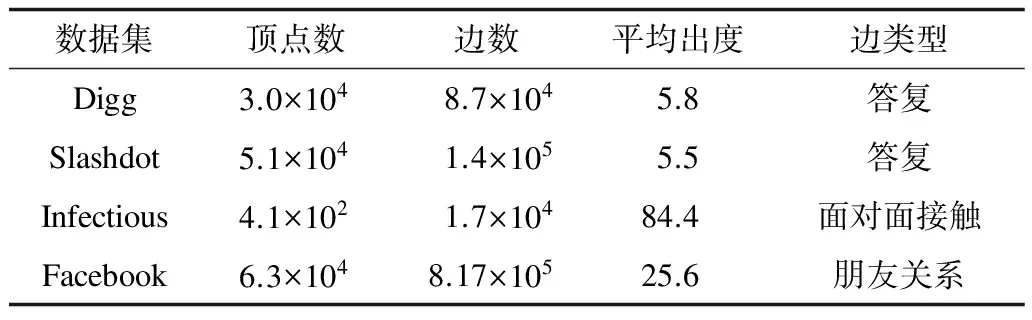
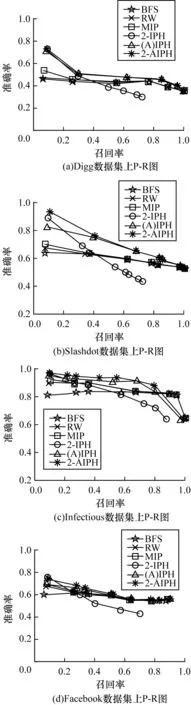
定义2(时间传播路径) 在给定的时间传播网络G={V,E}中,时间传播路径是一边序列P=<(v1,v2,t1,d1),(v2,v3,t2,d2),…,(vk-1,vk,tk,dk)>,∀(vi,vi+1,ti,di)∈P(1≤i 如图1中<(B,D,3,2),(D,F,5,2),(F,I,8,3)>是B到I的一条时间传播路径,但B不能通过<(B,E,4,3),(E,F,9,3),(F,I,8,3)>将信息传递给I,因为边(F,I,8,3)不符合时间约束。 在信息传播中,信息通过路径从传播网络的少量初始受影响顶点开始传播影响其他顶点,从而扩大信息影响范围。在IC模型中,顶点被信息影响后将保持受影响状态而不会改变,顶点状态为布尔值:受影响,不受影响。布尔函数f(v,γ,T)用于表示信息传播后TDN中顶点v在时间T时对信息γ的受影响状态。时间传播网络G中满足f(v,γ,T)=1的顶点构成T时受影响顶点集合S。 由于受影响概率越大越易成为受影响顶点,因此本文使用顶点受影响概率作为预测依据。由于TDN中顶点受影响概率随时间T和受影响顶点集合I改变,因此TDN中顶点受影响概率定义为: 定义4(顶点受影响概率) 时间传播网络中顶点受影响概率φ((I,v)|T)为时间T时顶点v被受影响顶点集合I中顶点影响的概率。 假设P= (1) 传播路径的传播概率计算是顶点受影响概率计算的基础。当候选顶点只有一条时间传播路径时,顶点的受影响概率等于该路径的传播概率。 当从受影响顶点到待计算顶点有多条时间传播路径时,可以将其分为重叠传播路径和无重叠传播路径。无重叠传播路径的定义如下: 定义5(无重叠传播路径) 在时间传播网络G中,对于到达顶点v的时间传播路径{P1,P2,…,Pl},若任意2条路径除了起点和终点v并没有其他相同顶点,则到顶点v的路径为无重叠传播路径。 假设受影响顶点集合I在时间T内到顶点v的时间传播路径{P1,P2,…,Pl}为无重叠传播路径。由于IC模型中无重叠传播路径之间相互独立,因此顶点v的受影响概率为: (2) 其中,δ(Pk)为通过式(1)计算得到的受影响顶点在时间T内到顶点v的时间传播路径Pk的传播概率。 在影响力最大化问题许多研究中,计算顶点受影响概率时假设传播路径之间都是相互独立的。如DynaDiffuse[10],其在边和传播路径都相互独立的假设下,在连续时间上计算动态传播网络中顶点影响力并解决影响力最大化问题。文献[21]介绍了静态传播网络中顶点受影响概率的准确计算方法。该文提出的Inclusion-Exclusion方法满足IC模型的边独立而路径不独立的假设。但是该方法是在静态传播网络中提出的,而在TDN中,由于存在时间因素,此计算方法并不完全适用。本文基于Inclusion-Exclusion计算思想,在TDN中计算任意顶点的受影响概率,具体过程如下: 在TDN中,每个顶点存在多个受影响时间Ti(接收时间Tv)。假设已知顶点v在时间Ti时的受影响概率为φ((I,v)|Ti),而顶点v在Ti+1时(时间传播网络G中顶点下一信息接受时间)从入边相邻顶点vx(vx∈Nin(v))经边e(vx,v,tx,dx)获得信息,tx+dx=Ti+1。由于边之间相互独立,因此顶点v在时间段Ti到Ti+1的受影响概率增量φ((I,v)|(Ti,Ti+1))和v在Ti+1时的受影响概率可以通过式(3)和式(4)计算得到,顶点v最早受影响时间T1时的受影响概率可通过式(5)计算得到。其中,边e(vx,v,tx,dx)为T1时到达顶点v的入边,边e(vx,v,tx,dx)满足tx+dx=T1。 φ((I,v)|(Ti,Ti+1))=1-∏(1-φ((I,vx)|Tx)ξ(e(vx,v,tx,dx))) (3) φ((I,v)|Ti+1)=φ((I,v)|Ti)+(1-φ((I,v)|Ti))φ((I,v)|(Ti,Ti+1)) (4) φ((I,v)|(T1))=1-∏(1-φ((I,vx)|Tx)·ξ(e(vx,v,tx,dx))) (5) 在利用式(3)~式(5)计算顶点受影响概率时,需要递归计算前一状态的受影响概率直到vx为受影响顶点。在信息传播过程中,由于顶点不能经其他顶点再影响自己,因此在递归计算时要避免环路的出现。在计算顶点受影响概率过程中,若顶点只有一条时间传播路径或是无重叠传播路径顶点时,可利用式(1)和式(2)计算顶点受影响概率。 在TDN中,为计算顶点的受影响概率,从受影响顶点到待计算顶点之间所有时间传播路径上经过顶点的受影响概率需要预先求得。由定理1可知,在TDN中计算顶点受影响概率是#P-hard问题。 定理1在时间传播网络中计算顶点受影响概率是#P-hard问题。 证明:在时间传播网络中查找两顶点间所有时间传播路径,相当于在普通有向图中找出两顶点间所有路径并剔除其中不符合时间约束的路径。由于在有向图中查找统计两顶点间所有路径是#P-complete问题[22],因此在时间传播网络中查找两顶点之间所有时间传播路径是#P-hard问题。而在时间传播网络中计算顶点受影响概率时,待计算顶点和受影响顶点间所有传播路径需要被遍历,因此,在时间传播网络中计算顶点受影响概率是#P-hard问题。 在TDN中,当每条边具有相同的传播概率ξ时,若顶点u到顶点v有2条时间传播路径P1和P2,则δ(P1)=ξ|P1|,δ(P2)=ξ|P2|,此时若|P1|>|P2|,则δ(P1)<δ(P2)。因此,可以得到如下结论: 结论1在TDN中,如果每条边具有相同的传播概率,则跳数较小路径的传播概率在终点受影响概率的计算中占较大比例。 结论2在TDN中,如果每条边具有相同的传播概率,则各跳数路径中路径条数都更多的顶点有更大的受影响概率。 基于以上结论,本文提出跳数受限近似(HLA)算法来近似计算顶点受影响概率,定义如下: 定义6(跳数受限近似算法) 对于给定的跳数限制参数h,未受影响顶点的受影响概率通过离受影响顶点跳数小于h的时间传播路径近似计算得到。 在计算过程中,为减少计算所需时间,HLA方法使用式(2)近似计算顶点受影响概率,具体过程为:首先找出时间传播网络G中从受影响顶点到待计算顶点h跳内无环时间传播路径,然后利用式(2)计算概率作为顶点受影响概率。 虽然在影响力最大化问题中,也有许多近似方法被提出,但大部分是为解决组合最优问题而构造的,因此,这些方法在受影响顶点预测中并不十分有效。如PMIA[9]中基于MIA模型使用最大传播路径(Maximum Propagation Path,MIP)评估顶点影响力。MIP在受影响顶点预测中相当于贪心选择受影响顶点出边中传播概率最大的边的相邻顶点作为下一验证顶点。但由于待计算顶点与受影响顶点之间可能存在多条传播路径,MIP选择的顶点并不一定是受影响概率最大的顶点。而利用HLA近似计算选择顶点时,当h不小于TDN中最长路径的跳数时,其选择的顶点为受影响概率最大的顶点,当h值为一有限值时选择的顶点仍为受影响概率较大顶点。参数h的大小是HLA算法有效性与可行性的折中,h值对受影响顶点预测的影响将在实验中进行比较。 本节将介绍基于HLA近似算法的受影响概率启发式预测算法IPH。该算法主要由受影响概率计算(Infection Probability Calculation,IPC)算法和候选集合更新(Candidate Set Update,CSU)算法构成。在受影响顶点预测中,候选集合中受影响概率最大的顶点将进行顶点状态验证。 受影响顶点的可达顶点查找以及受影响概率计算是受影响顶点预测发现的重点,本文提出受影响概率计算算法IPC来查找可达顶点并计算受影响概率。对受影响集合I中顶点调用IPC算法后得到受影响集合I的可达顶点集合即候选集合。 在利用HLA近似算法近似计算顶点受影响概率时需满足以下条件:1)时间传播路径的跳数不能超过h;2)在IC模型中每个顶点只能被影响一次,因此,每个顶点在时间传播路径中最多只能出现一次,所以,候选集合C由从受影响顶点出发没有重复顶点与其他受影响顶点的路径跳数小于h的可达顶点构成。由于DFS算法在遍历图时能够将经过的顶点记录在堆栈中从而避免环路的出现,因此IPC算法基于DFS算法在TDN中查找符合条件的时间传播路径。 在根据HLA近似算法计算顶点受影响概率时,若已知顶点v的受影响概率为φ((I,v)|T),此时若有另一经相邻顶点u到v的传播路径且u的受影响概率为φ((I,u)|Tu),那么顶点v的受影响概率为: φ((I,v)|T)= 1-(1-φ((I,v)|T))× (1-φ((I,u)|Tu)×ξ(e)) (6) 其中,ξ(e)是u到v的边的传播概率。若顶点u为受影响顶点,则式(6)可简化为:φ((I,v)|T)=1-(1-φ((I,v)|T))×(1-ξ(e))。 算法1为受影响概率计算算法IPC的伪代码。若得到的可达顶点v不在候选集合C中,则v将加入候选集合C,其受影响概率由式(6)计算得到;若顶点v已经在候选集合C中,则其受影响概率根据式(6)更新计算得到。在候选集合C中将记录候选顶点各到达时间的受影响概率用于后续的计算,C.Update()函数将更新候选集中顶点v在到达时间t+d后各时刻的顶点受影响概率。 算法1受影响概率计算算法IPC 输入时间传播网络G,边上传播概率ξ(E),起始顶点u,顶点u的受影响概率prob(u),开始时间t,结束时间T,已验证顶点集合L,候选集合C,跳数h 输出候选集合C 1.Stack S={u;t;prob(u)},List Visited_Edges=Ø; 2.while (S≠Ø and S.size() 3. (u′,t′,prob(u′))=S.Pop(); 4. 获得顶点u′在t′之后不指向S中顶点的出边E′; 5. if (E′-(E′∩Visited_Edges)≠Ø) 6. e(u′,v,t,d)=Earliest(E′-E′∩Visited_Edges); 7. prob(v)=prob(u′,t)*ξ(e); 8. if (v∈C) 9. C.Update(v,prob(v),t + d); 10. prob(v)=1-(1-C.Prob(v))*(1-prob(v)); 11. C.Set(v,prob(v)); 12. else 13. C.Add(v,prob(v)); 14. S.Push({v,t+d,prob(v)}),Visited_Edges.Add(e); 15. else 16. S.Pop(); 17.end while 18.return C; 在受影响顶点预测中,由于信息传播具有随机性和不确定性,因此需要结合顶点状态验证来确认受影响顶点,即选择候选集合C中受影响概率最大的顶点进行顶点状态验证。而经过顶点状态验证,候选顶点的受影响概率将会改变,顶点状态验证对候选集合的改变如定理2所述。因此在顶点状态验证后需要更新候选集合。 定理2顶点状态验证后,候选集合始终减小。 证明:在时间传播网络中,候选集合C由受影响顶点的所有可达顶点构成。在顶点状态验证后,被验证顶点v将从候选集合中移除。若顶点v是受影响顶点,顶点v的可达顶点受影响概率将增大,但由于v的可达顶点也是原受影响顶点的可达顶点,因此候选集合并不会增大;而若顶点v不是受影响顶点,v可达顶点的受影响概率将减小,受影响概率变为0的顶点将从候选集合中移除,候选集合进一步减小。因此,顶点状态验证后,候选集合始终减小。 最简单直接的候选集合更新方法是将验证顶点v加入已验证顶点集合L后调用IPC算法重新计算候选集合。但是该方法较耗计算资源且候选集合C中只有验证顶点的可达顶点会改变。为提高算法计算效率,本文提出了CSU候选集合更新算法来更新候选集合。 假设顶点v′是验证顶点v的可达顶点,v到v′的传播路径为{P1,P2,…,Pi}且已知顶点v在各到达时间v.timej时的受影响概率为v.probj,那么顶点v′经顶点v被受影响顶点影响的概率可由式(7)计算得到。 (7) 其中,Pi为v.timej后顶点v到v′的时间传播路径。 若顶点v被验证为非受影响顶点,那么顶点v′的受影响概率更新为: (8) 若顶点v被验证为受影响顶点,那么顶点v′的受影响概率更新为: (9) 其中,Pi为顶点v受影响时间后的时间传播路径。 在使用HLA近似算法时,由于只有受影响顶点的h跳内可达顶点被包含在候选集合C中,因此在顶点状态验证后若顶点被验证为受影响顶点,则需要将不在候选集合C中的验证顶点h跳内可达顶点加入候选集合C。 CSU候选集合更新算法的伪代码如算法2所示。IPC算法可用于计算顶点v各到达时间区间内可达顶点的受影响概率,因此,CSU算法调用IPC算法查找被验证顶点v的可达顶点集合C1并计算受影响概率。在获得集合C1后,利用式(8)和式(9)更新顶点v可达顶点的受影响概率,从而更新候选集合C。在Increase函数中,不在候选集合C中的可达顶点将加入候选集合C。 算法2候选集合更新算法CSU 输入时间传播网络G,边上传播概率ξ(E),验证顶点v,结束时间T,已验证顶点集合L,候选集合C,跳数h 输出候选集合C 2.for ( each (t1,t2,prob(v,t1)) in C.Each(v) ) 3. C1=IPC(G,ξ(E),v,t1,prob(v,t1),t2,L,C1,h); 4.end for 5.Decrease(C,C1); 6.if (f (v,γ,T)) 7. C2=C1.After(v.InfectedTime ); 8. Increase(C,C2); 9. C.Remove(v); 10.return C; 受影响概率启发式预测算法IPH的伪代码如算法3所示。IPH算法由两部分构成:初始阶段和预测验证阶段。在初始阶段,调用受影响概率计算算法IPC对每个初始受影响顶点查找其可达顶点并计算可达顶点的受影响概率,从而获得初始候选集合;在预测验证阶段,受影响概率最大的候选顶点将进行顶点状态验证确定其是否被影响,在验证之后调用候选集更新算法CSU来更新候选集合。利用IPH算法将得到k次验证后的验证顶点集合L,从而明确哪些顶点确实成为受影响顶点。 算法3受影响概率启发式预测算法IPH 输出已验证顶点集合L 3. C=IPC(G,ξ(E),ui,ti,1,T,L,C,h); 4.end for 6. v=C.MaxProb(); 7. Node_State(v,γ,T);//顶点状态验证 8. L.Add(v,f(v,γ,T)?v.InfectedTime:-1); 9. C=CSU(G,ξ(E),v,T,L,C,h);//更新候选集合 10.end while 11.return L; 在TDN中,只有在最早开始传播时间和结束时间内的接触才能传播信息,因此,在使用IPH算法预测受影响顶点前可以对TDN进行时间图过滤预处理,即只保留有效时间段内的边,该过程能有效缩短计算时间。 在IPH算法中,HLA近似算法被用于计算初始受影响顶点h跳内可达顶点的受影响概率,并构造候选集合C。在获得候选集后,受影响概率最大的顶点将进行顶点状态验证。但是随着顶点逐渐被选择验证,候选顶点的受影响概率逐渐趋于相同,同时受影响顶点在候选集合中所占的比例也在逐渐降低,此时使用HLA近似算法计算得到的顶点受影响概率并不能很好地将受影响顶点与非受影响顶点区分开。因此,IPH算法在验证次数k较大时,预测性能不佳。本文基于BFS算法顶点选择策略提出相邻顶点受影响概率启发式预测算法AIPH来解决该问题。AIPH算法与IPH算法的区别在于:AIPH算法在选择顶点时只选择候选集合C中受影响概率最大的受影响顶点的相邻顶点进行验证。AIPH算法的候选集合计算与更新与IPH算法相同,因此,其时间复杂度也相同。 本文在真实数据集和模拟数据集上比较IPH算法、AIPH算法和现有算法在受影响顶点预测上的性能,对比算法如下: 1)广度优先遍历算法(BFS)。BFS算法是顶点遍历中最常用的算法且信息传播具有广度传播特点,因此,选择BFS算法作为对比算法。 2)随机游走算法(RW)。随机游走算法是图上抽样算法的代表算法[10],在随机游走过程中,边上传播概率作为随机游走的概率进行顶点选择。 3)最大传播路径方法(MIP)。PMIA[9]是影响力最大化问题中比较具有代表性的算法,其中的MIP算法可用于受影响顶点预测。MIP在受影响顶点预测中等价于贪心选择传播概率最大边的相邻顶点作为下一验证顶点。 4)IPH算法。IPH算法利用HLA近似计算顶点受影响概率,因此,用x-IPH表示跳数h设为x的IPH算法。 5)AIPH算法。类似于IPH算法,x-AIPH表示跳数h设为x的AIPH算法。当h为1时,1-AIPH和1-IPH算法相同,用(A)IPH进行表示。 边上传播概率映射:在传播网络中可由用户行为分析[2],传播概率推测[3]和传播网络推测[4-6]等研究成果推测边上传播概率。本实验中使用文献[5,10]中常用的指数模型进行边上传播概率映射,即使用βe-d(T-t)计算TDN边上传播概率。 信息传播模拟:由于信息传播渠道复杂等原因,信息传播在真实环境中难以跟踪获取,因此本实验在数据集上模拟信息传播。在模拟过程中,随机选择若干顶点作为初始受影响顶点,然后以边上传播概率映射得到的概率进行传播,从而获得信息传播模拟结果。传播模拟结果将作为受影响顶点预测实验的验证集,而数据集和初始受影响顶点集合则作为实验输入。 本实验使用文献[5,11]实验中使用的3种Kronecker图生成模拟数据集:Random([0∶5;0∶5;0∶5;0∶5]),Hierarchical([0∶9;0∶1;0∶1;0∶9]),Coreperiphery([0∶9;0∶5;0∶5;0∶3])。在构造模拟数据集时,实验结合SNAP中静态Kronecker图生成算法产生1×103个顶点和10×103条边的模拟时间传播网络。 图2是已知TDN边上传播概率条件下在模拟数据集上的实验结果。图中横坐标R=k/|S|是顶点验证次数k与实际受影响顶点数|S|的比值。图2(a)~图2(c)是各算法在不同验证次数时召回率的变化曲线,图2(d)~图2(f)是各算法在不同验证次数时准确率的变化曲线。从召回率图中可发现各算法召回率在开始时近似于线性增加,但在召回率超过80%后增长速度明显下降趋于对数增长。相较于其他算法,IPH在顶点验证次数较大的情况下召回率并不高,但改进后的AIPH算法则有较好的性能,即在k值较大情况下召回率与BFS算法相差无几。从准确率图中可发现IPH算法在准确率上要明显强于其他算法,当顶点验证次数k较小时IPH算法和AIPH算法准确率比其他对比算法高10%~20%。图2(g)~图2(i)为准确率与召回率变化图,从中可以看出,IPH算法和AIPH算法优于MIP算法,而MIP算法接近但略优于随机游走算法,BFS算法则性能最差。在k值较小时IPH算法和AIPH算法相差无几,但AIPH算法在k较大时较稳定,因此,AIPH算法能更好地解决受影响顶点预测问题。对于HLA近似算法参数值h,从实验中可发现较大的h值能够提高IPH算法和AIPH算法顶点选择准确性但提高幅度不大,由此可见利用HLA近似算法得到的顶点顺序接近于顶点按实际受影响概率排序得到的顺序。 在信息传播预测中,边上传播概率并不一定能够准确计算得到,图3为当边上传播概率未知(假设边上传播概率均为0.5)时各算法在模拟数据集上的结果。在BFS算法中顶点选择并不受边上传播概率影响,因此,图2和图3中BFS算法的结果是相同的。对于MIP算法,由于边上传播概率相同MIP算法随机从相邻顶点选择顶点,因此退化为BFS算法,其实验结果确实与BFS算法十分吻合。而对于IPH算法和AIPH算法,虽然准确率有所下降,但相较于其他算法仍有较高的准确率。 图2 模拟数据集边上传播概率已知时的召回率和准确率 图3 模拟数据集边上传播概率未知时的召回率和准确率 实验结果表明,IPH算法和AIPH算法在受影响顶点预测上有更好的性能,尤其是AIPH算法,其在k较大时准确率和召回率仍略优于BFS算法。 本实验使用图数据集网站konect (http://konect.uni-koblenz.de/)上的4个数据集:Digg,Slashdot,Infectious和Facebook。对于这4个真实数据集,需要先进行数据补全、传播模拟等预处理后再进行受影响顶点预测。数据集的统计信息如表1所示。 表1 真实数据集 真实数据集上的实验结果如图4所示。可以看出,数据集上,IPH算法和AIPH算法相对于其他方法仍有较好的实验结果,能准确地预测受影响顶点。 图4 真实数据集已知边上传播概率时的召回率和准确率 本文将传播网络定义为时间传播网络,并研究其中基于IC模型的顶点受影响概率计算方法与受影响顶点预测方法。针对顶点受影响概率计算这一#P-hard问题,利用HLA算法近似计算顶点受影响概率,提出IPH算法预测受影响顶点,并结合BFS策略进一步给出AIPH算法。实验结果表明,本文算法能有效预测受影响顶点。鉴于本文基于IC模型和封闭世界假设等约束进行研究,下一步将考虑在更少的约束条件下预测受影响顶点。 [1] HOLME P,SARAMKI J.Temporal Networks[J].Physics Reports,2012,519(3):97-125. [2] ZHANG Jun,WANG Chaokun,WANG Jianmin,et al.Inferring Continuous Dynamic Social Influence and Personal Preference for Temporal Behavior Prediction[J].Proceedings of VLDB Endowment,2014,8(3):269-280. [3] GOMEZ R M,LESKOVEC J,KRAUSE A.Inferring Networks of Diffusion and Influence[J].ACM Transac-tions on Knowledge Discovery from Data,2010,5(4):1019-1028. [4] ABRAHAO B,CHIERICHETTI F,KLEINBERG R,et al.Trace Complexity of Network Inference[C]//Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York,USA:ACM Press,2013:491-499. [5] GOMEZ R M,BALDUZZI D,SCHÖLKOPF B,et al.Uncovering the Temporal Dynamics of Diffusion Networks[C]//Proceedings of the 28th International Conference on Machine Learning.[S.l.]:International Machine Learning Society,2011:561-568. [6] RONG Yu,ZHU Qiankun,CHENG Hong.A Model-free Approach to Infer the Diffusion Network from Event Cascade[C]//Proceedings of the 25th ACM Inter-national on Conference on Information and Knowledge Management.New York,USA:ACM Press,2016:1653-1662. [7] LESKOVEC J,FALOUTSOS C.Sampling from Large Graphs[C]//Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York,USA:ACM Press,2006:631-636. [8] MEHDIABADI M E,RABIEE H R,SALEHI M.Sampling from Diffusion Networks[C]//Proceedings of International Conference on Social Informatics.[S.l.]:AAAI,2012:106-112. [9] CHEN Wei,WANG Chi,WANG Yajun.Scalable Influence Maximization for Prevalent Viral Marketing in Large-scale Social Networks[C]//Proceedings of Inter-national Conference on Social Informatics.New York,USA:ACM Press,2010:1029-1038. [10] XIE Miao,YANG Qiusong,WANG Qing,et al.DynaDiffuse:A Dynamic Diffusion Model for Continuous Time Constrained Influence Maximization[C]//Pro-ceedings of the 29th AAAI Conference on Artificial Intelligence.[S.l.]:AAAI,2015:346-352. [11] DU Nan,LIANG Yingyu,Balcan M F,et al.Influence Function Learning in Information Diffusion Networks[C]//Proceedings of International Conference on Machine Learning.Beijing,China:[s.n.],2014:2016-2024. [12] RODRIGUEZ M G,SCHÖLKOPF B.Influence Maximization in Continuous Time Diffusion Networks[J].Cement and Concrete Composites,2012,34(5):684-691. [13] NAJAR A,DENOYER L,GALLINARI P.Predicting Information Diffusion on Social Networks with Partial Knowledge[C]//Proceedings of the 21st International Conference Companion on World Wide Web.Lyon,France:[s.n.],2012:1197-1204. [14] GUILLE A.Information Diffusion in Online Social Networks[C]//Proceedings of SIGMOD/PODS’13.New York,USA:[s.n.],2013:31-36. [15] KEMPE D,KLEINBERG J,TARDOS É.Maximizing the Spread of Influence Through a Social Network[C]//Proceedings of the 9th ACM SIGKDD.New York,USA:ACM Press,2003:137-146. [16] IWATA T,SHAH A,GHAHRAMANI Z.Discovering Latent Influence in Online Social Activities via Shared Cascade Poisson Processes[C]//Proceedings of SIGKDD’13.New York,USA:ACM Press,2013:266-274. [17] GOMEZ R M,LESKOVEC J,SCHÖLKOPF B.Structure and Dynamics of Information Pathways in Online Media[C]//Proceedings of ACM WSDM Conference.New York,USA:ACM Press,2012:23-32. [18] 曹玉林,马建萍.基于微分方程的移动自组网病毒传播模型研究[J].计算机工程,2017,43(1):172-177. [19] 曹玖新,吴江林,石 伟,等.新浪微博网信息传播分析与预测[J].计算机学报,2014,37(4):779-790. [20] WU Huanhuan,CHENG J,HUANG Silu,et al.Path Problems in Temporal Graphs[J].Proceedings of the VLDB Endowment,2013,7(9):721-732. [21] ZHANG Miao,DAI Chunni,DING C H,et al.Probabilistic Solutions of Influence Propagation on Social Networks[C]//Proceedings of the 22nd ACM International Conference on Information and Knowledge Management.New York,USA:ACM Press,2013:429-438. [22] VALIANT L G.The Complexity of Enumeration and Reliability Problems[J].SIAM Journal on Computing,1979,8(3):410-421.
2.2 问题定义


2.3 TDN中顶点受影响概率计算

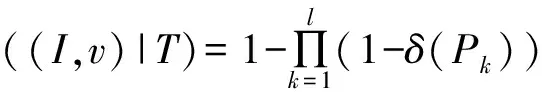
2.4 受影响概率近似计算
3 IPH算法
3.1 IPC算法
3.2 候选集合更新

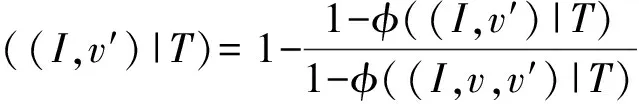
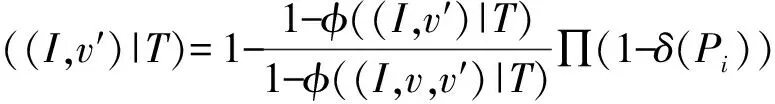
3.3 IPH算法与复杂度分析

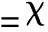
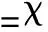
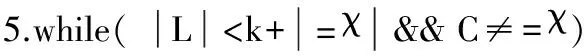
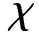
3.4 AIPH算法
4 实验与结果分析
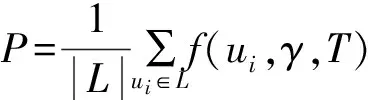
4.1 模拟数据集上的实验分析


4.2 真实数据集上的实验分析
5 结束语

