正方形边上三等分点的一种新折法及其拓展探究

上海师范大学(200234)沈越

1 前言

在折纸数理学中,芳贺的三个定理展示了三种在正方形的边上折三等分点的方法.笔者通过观察发现,这三种折法的共同之处在于都利用了正方形上边的中点.于是笔者思考,能否利用正方形的中心来进行折叠,得到正方形边上的三等分点呢?经过探究,笔者发现了一种新的折法,可以用来折出正方形边上的三等分点.此外,笔者还将这种折法运用于一般长方形,并将这种折法稍加变形后再运用于正方形,得出了一些有意义的结论.特别地,笔者给出了在正方形边上折n等分点的一种方法.

2 一种新的折正方形边上三等分点的折法

操作1 在正方形ABCD中,将CD与AB重合对折,折痕为EF;再将AB、CD分别与EF重合对折,折痕分别为GH、MN,如图1所示;

图1

图2

操作2 以MH为折痕,将梯形CDMH向上翻折,CH翻折后的对应边C′H与AB交于点K,如图2所示,则K点是边AB上的三等分点.

为了叙述方便,下文统一将这种新折法称为该折法.现对该折法折出的点K是AB边上三等分点进行证明,证明如下:

易知MH过正方形中心O.令AB边中点为P,连接OP、OK、OF,并作OS⊥KH交KH于点S(如图3所示).令大正方形ABCD边长为2a,则小正方形OPBF边长为a,BH=HF=设BK=x,则PK=a−x.此外,由于∠OHS=∠OHF,∠OSH=∠OFH=90°,OH=OH,故△OSH∼=△OFH(a.a.s.),OS=OF=a.又由于OS=OP=a,OK=OK,∠OSK=∠OPK=90°,故△OSK∼=△OPK(h.l.),SK=PK=a−x.在Rt△KBH中运用勾股定理,有

图3

3 该折法在一般长方形中的拓展探究

设长方形ABCD的边AB=2a,AD=2ka.对长方形ABCD运用该折法进行折叠,得到CH的对应边C′H与AB的交点K.为了探求K在AB上的位置,同样,我们将长方形ABCD的中心O分别与AB边上中点P、BC边上中点F进行连接,得到了小长方形OPBF,其中BP=a,OP=ka(如图4所示).由于在小长方形OPBF中,该折法的折叠过程与芳贺第二定理的折叠过程一致,故直接运用文[1]中“芳贺第二定理在一般长方形中的拓展探究”的结论,当k＜2时有

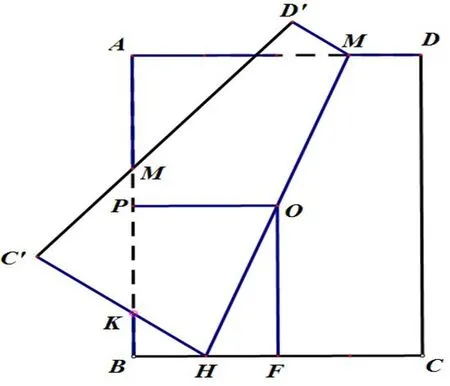
图4

图5

4 对该折法在正方形中变形的拓展探究

通过观察笔者发现,该折法的折痕不仅通过正方形的中心O,而且与正方形的边AD、BC的交点也是特殊点(M、H分别是AD、BC边上的四等分点),于是笔者设想,如果只保留折痕过正方形中心O点的性质,而不要求其过AD、BC边上的四等分点,C′H与AB的交点K在AB上的位置是否有某些更一般的结论?为此,笔者在正方形中进行了如下操作:

操作3 在正方形ABCD中,将CD与AB重合对折,折痕为EF;将AD与BC重合对折,折痕为PQ.记PQ与EF的交点为O,则O是正方形ABCD的中心,如图6所示.

操作4 在BF上任取一点H,连接HO并延长使之与AD交于点M.以MH为折痕,将梯形CDMH向上翻折,CH的对应线段C′H与AB交于点K,如图7所示.

图6

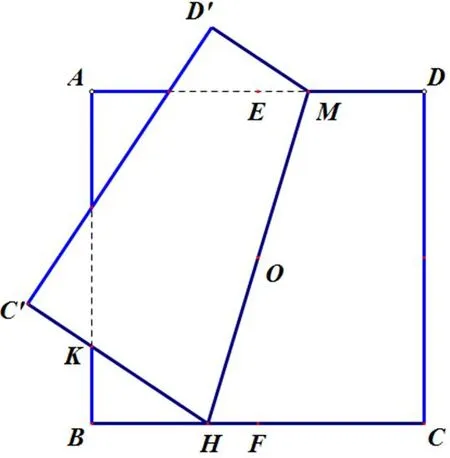
图7

图8

易有折痕MH过正方形中心O点.为了探求K在AB上的位置,我们连接OP、OK、OF,并作OS⊥KH交KH于点S(如图8所示).令大正方形ABCD边长为2a,则小正方形OPBF边长为a.设HF=ta,BK=x,则BH=a−ta,PK=a−x.此外,由于∠OHS=∠OHF,∠OSH=∠OFH=90°,OH=OH,故△OSH∼=△OFH(a.a.s.),HS=HF=ta,OS=OF=a.又由于OS=OP=a,OK=OK,∠OSK=∠OPK=90°,故△OSK∼=△OPK(h.l.),SK=PK=a−x.在Rt△KBH中运用勾股定理,有

作为结论,我们有:当该折法的折痕绕正方形中心O点旋转时,K点分AB边的比值同折痕MH与正方形边AD、BC的交点M、H的位置有关,且等于特别地,当H取BF的中点时,有故可知该折法能折出AB边上的三等分点K.此外,若要折AB边上的四等分点、五等分点、六等分点K等等,只需相应地先找到BF边上靠近F那一侧的三等分点、四等分点、五等分点H等等,然后连接HO并延长使之交AD于M,再以MH为折痕将梯形CDMH向上翻折即得.从理论上来看,通过折纸找AB边上的n等分点可以在有限步内完成:先利用中点寻找三等分点,再利用三等分点寻找四等分点等等,直到利用(n−1)等分点寻找n等分点.

5 结语

本文给出了在正方形边上折三等分点的一种新折法,并通过将该折法运用于一般长方形以及稍加变形后运用于正方形中的拓展探究,得到了一些有意义的结论,特别是在最后笔者给出了在有限步内,通过层层递进的方式折正方形边上n等分点的方式,值得读者做进一步的深思与研究.

此外,若将本文中的折纸方法用于几何教学(特别是全等三角形、勾股定理的教学),设计一些以小组合作为方式的探究活动,可极大地提升学生迁移与运用所学数学知识的能力,增加他们学习数学的兴趣.相信老师与学生们在合作探究的过程中,会发现更多新奇有趣的结果,感受到折纸的魅力!

[1]沈越.芳贺第一与第二定理在一般长方形中的拓展探究.[J].上海中学数学,2016.(06):19-21