例谈构造函数法破解高考函数导数压轴题

广东省佛山市第一中学(528000)吴统胜

广东省佛山科学技术学院数学与大数据学院(528000)杨豫晖

本文笔者将结合高考题重点举例说明如何利用构造函数的通法破解函数导数压轴题,重点讲述解题思路的突破,即如何结合题目已知条件及求证去恰当构造函数破解函数导数压轴题.另外,笔者还就函数导数压轴题的高考复习备考给出了一些相当有益的、建设性的建议.

一、直接构造函数法

例1 (2013年课标II理科21)已知函数f(x)=ex-ln(x+m).

(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;

(2)当m≤2时,证明:f(x)＞0.

解析(1)略;

(2)当m≤2时,f(x)=ex-ln(x+m)≥ex-ln(x+2),将要证f(x)＞0转化为证明ex-ln(x+2)＞0.

直接构造函数φ(x)=ex-ln(x+2),转化为求证φ(x)min=φ(x0)＞0,但使对应的x0不可求出,需利用零点存在定理及设而不求法求得最小值,只需证明φ(x)min=φ(x0)＞0.其证明过程如下:

当m≤2时,f(x)=ex-ln(x+m)≥ex-ln(x+2).设φ(x)=ex-ln(x+2),则在(-2,+∞)上单调递增.又φ′(-1)＜0,φ′(0)＞0,所以φ′(x)=0在(-2,+∞)上有唯一实根x0,且x0∈(-1,0).当x∈(-2,x0)时,φ′(x)＜0;当x∈(x0,+∞)时,φ′(x)＞0,所以φ(x)min=φ(x0).由φ′(x0)=0得:ln(x0+2)=-x0,所以

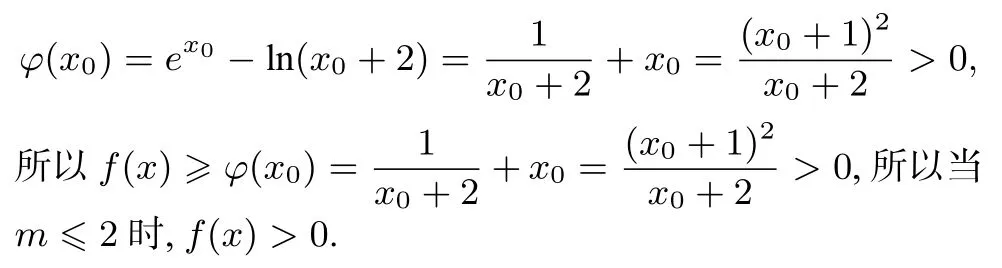
点评此方法直接转化为求函数的最小值,思路清晰,但由于最小值φ(x0)对应的x0不可求,为隐性零点,需利用零点存在定理及设而不求法巧妙地破解了该证明问题.

二、结合某些常见函数构造新函数

构造函数证明问题的关键技巧之一是:结合含ex,lnx(x＞0)的组合函数的图像和性质恰当变形转化,或利用常见函数型不等式进行放缩.

题目同例1

解析先利用常见函数型不等式ex≥x+1或lnx≤x-1(x＞0)进行放缩,再构造函数证明,其证明过程如下:

当m≤2时,f(x)=ex-ln(x+m)≥ex-ln(x+2).因为ex≥x+1,当且仅当x=0时取等号,所以f(x)=ex-ln(x+m)≥ex-ln(x+2)≥x+1-ln(x+2).设φ(x)=x+1-ln(x+2)(x＞-2),易证φ(x)min=φ(-1)=0.因为两不等式等号不同时取得,所以当m≤2时,f(x)＞0.

点评本题也可同时利用常见函数型不等式ex≥x+1及lnx≤x-1(x＞0)进行放缩,原不等式可轻松得证！

例2 (2017年佛山二模理科第21题)设函数f(x)=aex-xlnx,其中a∈R,e是自然对数的底数.

(1)若函数f(x)是(0,+∞)上的增函数,求实数a的取值范围;

解析(1)略.(2)因为若直接构造函数即转化证明:当时,F(x)min＞0.因为

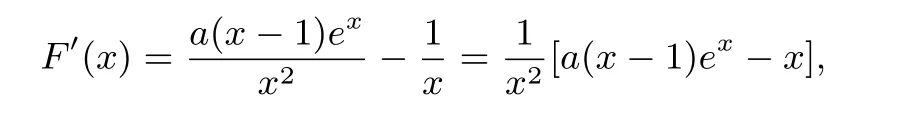
令F′(x)=0,所以a(x-1)ex=x,故需要对x就0＜x≤1和x＞1分类讨论,证明过程相对较复杂.可考虑先对原不等式进行适当变形,再构造函数法证明.

证法一优先消去参数a,联想到组合函数图像和性质,对要证不等式进行恰当变形,再构造函数证明,其证明过程如下:

证法二先利用常见函数型不等式进行适当放缩,再构造函数证明.观察要证不等式结构特征,可先利用函数型不等式进行放缩,再构造函数证明,其证明过程如下:

例3 (2017年广州一模理科第21题)已知函数

(1)若函数f(x)有零点,求实数a的取值范围;

解析(1)(略)

(2)证法一适当变形后,构造函数证明.

设t=lnb,因为b＞1,所以t＞0.即证必须分开,否则直接构造函数求导之后单调性无法或不便于讨论,转化证明不了！原不等式即证如何变形转化证明呢?找寻突破口！联想到组合函数的图像和性质,恰当变形转化为证明(破解最关键一步！找寻解题突破口并不盲目！)转化为两个函数的最大、最小值的大小比较问题,再构造函数得证！设所以φ(x)≥h(x).原不等式得证！

点评该证明方法相当巧妙！极大地简化思维量和运算量！可见构造函数法在证明函数导数压轴题中的强大威力！此类同时含有ex,lnx的不等式常可采用该转化为两个函数最值大小比较问题的证明方法.

证法二先利用常见函数型不等式进行放缩,再构造函数证明.

点评在该证明方法中,解决问题的关键首先在于通过换元转化为证明不等式再结合不等式结构特征巧妙利用函数型不等式et≥et和放缩得证！

其实该题改编自2014年全国I理科第21题:

(I)求a,b;(II)证明:f(x)＞1.

简析(I)(略)a=1,b=2;(II)由(I):f(x)=exlnx+要证f(x)＞1,即证以下证明过程同例3.

而2014年全国(I)理科第21题改编自2014黑龙江高中数学预赛题,其题目如下:

证明:对一切x∈(0,+∞)都有成立.

点评教师要重视并善于在全国数学竞赛题中发现好的题目资源,进行适当改编,就是一道好的高考训练题或高考题！

例4 已知函数f(x)=lnx,设b＞a＞0,求证:

例5 (2013陕西理科第21题)已知函数f(x)=ex,x∈R.(I)略.(II)略.

下面结合该题介绍处理二元不等式的另外一种行之有效的构造函数的证明方法–主元法,有时需要构造局部函数多次求导.

解析因为a＜b,所以b-a＞0,所以比较的大小,即比较(b-a)(ea+eb)与2(eb-ea)的大小,亦即比较(b-a)(ea+eb)-2(eb-ea)与0的大小.

以b为主元,视a为参数,记函数F(x)=(xa)(ea+ex)-2(ex-ea),x∈(a,+∞),求导得F′(x)=(x-a-1)ex+ea,F′′(x)=(x-a)ex＞0,得F′(x)在(a,+∞)上单调递增,F′(x)＞F′(a)=0,所以F(x)在(a,+∞)上单调递增,所以F(x)＞F(a)=0,即F(b)＞0,所以

点评主元法证明方法相当快速简捷,太绝太妙！可见利用主元法可轻松破解该类高考压轴题！主元法可操作性强,按部就班,考生容易掌握！当然,并非所有的二元不等式都可以用主元法轻松证得,主元法中的两“元”必须相互独立,否则不可以用主元法证明！

三、处理含参问题的常用方法

含参数问题,可优先考虑消去参数、换元,再利用构造函数法证明;有时还需要构造局部函数多次求导;也可考虑分离参数,再构造函数.常需分类讨论及用到高等数学中的洛必达法则.

例6 (2016年全国卷I第21题)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(I)求a的取值范围;

(II)设x1,x2是f(x)的两个零点,证明:x1+x2＜2.

解析(I)f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a).

(i)设a=0,则f(x)=(x-2)ex,f(x)只有一个零点.

(ii)设a＞0,则当x∈(-∞,1)时,f′(x)＜0;当x∈(1,+∞)时,f′(x)＞0.所以f(x)在(-∞,1)单调递减,在(1,+∞)单调递增.又f(1)=-e,f(2)=a,取b满足b＜0且则0,f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a).故f(x)存在两个零点.

(iii)设a＜0,由f′(x)=0,得x=1或x=ln(-2a).若则ln(-2a)≤1,故当x∈(1,+∞)时,f′(x)＞0,所以f(x)在(1,+∞)上单调递增,又当x≤1时,f(x)＜0,所以f(x)不存在两个零点.若则ln(-2a)＞1,故当x∈(1,ln(-2a))时,f′(x)＜0,当x∈(ln(-2a),+∞)时,f′(x)＞0.又当x≤1时,f(x)＜0,所以f(x)不存在两个零点.

综上:a的取值范围为(0,+∞).

(II)不妨设x1＜x2,由(I)知:x1∈(-∞,1),x2∈(1,+∞),2-x2∈(-∞,1).f(x)在(-∞,1)单调递减,所以x1+x2＜2即x1＜2-x2等价于f(x1)＞f(2-x2).因为f(x1)=0,所以f(2-x2)＜0(转化证明,解题突破口！)因为f(2-x2)=-x2e2-x2+a(x2-1)2,f(x2)=(x2-2)ex2+a(x2-1)2=0.所以f(2-x2)=-x2e2-x2-(x2-2)ex2(消元,以x2表示a,构造函数解题突破的关键一步！)构造函数g(x)=-xe2-x-(x-2)ex,(x＞1).因为x＞1,所以g′(x)=(x-1)(e2-x-ex)＜0=g(1),所以当x＞1时,g(x)＜0,所以g(x2)=f(2-x2)＜0,所以x1+x2＜2.

点评第(II)问将x1+x2＜2转化为f(x1)＞f(2-x2),进而通过构造辅助函数g(x)=f(2-x),研究辅助函数的单调性得到问题的证明！

例7 (2016年安庆模考卷)设函数h(x)=(x-1)2+mlnx(m∈R,且m/=0).若h′(x)有两个零点x1,x2(x1＜x2).证明:

点评本题难点在于整体代换得到关于零点x2的新函数h(x2),再对新构造的函数φ(t)求导、判断单调性,进而得到h(x2)的范围.