冲击载荷下硼酸改性端羟基聚硅氧烷- 二氧化硅复合材料的响应特性

周鼎， 苗应刚， 王严培， 李峰， 李玉龙

(1.西北工业大学 先进材料与结构研究所, 陕西 西安 710072; 2.西安理工大学 材料科学与工程学院, 陕西 西安 710048)

0 引言

针对具有优良抗冲击性能的轻型防护材料及装备的研究和开发受到日益增加的关注。液体防弹衣[1-3]就是轻型防护装备的典型代表，其所采用的剪切增稠液体是一类由液态的高分子基体(如聚乙二醇、聚乙烯醇)与微纳米级二氧化硅颗粒共同组成的液体系[4-5]。虽然液体防弹衣轻便并拥有良好的防护特性，但是溶剂呈液体状态、使用寿命短、抗老化性能及抗二次损伤性能弱等缺陷限制了其大规模的应用。近年来，以聚合物为基体制备的轻质抗冲击材料逐渐兴起[6-9]。其中，硅胶拥有良好的抗氧化、防潮和温度稳定性，是一种适合运用于户外的材料[10-11]。以硅胶系高分子材料端羟基聚硅氧烷(PDMS)为基体添加二氧化硅颗粒的复合材料具有良好的抗冲击性能和很大发展潜力[10, 12-13]。

为评估、改善材料抗冲击性能，进行材料动态力学性能测试以及其变形机理研究具有重要的意义。目前主要采用的测试手段有冲击试验[14-15]和基于分离式霍布金森压杆(SHPB)的动态压缩试验。Roché等[14]将金属杆放置于一定高度，利用金属杆自由落体冲击剪切增稠液体，观察到冲击作用触发了液态-固态转变。Jiang等[16]通过自由落体测试系统测试了一种冲击硬化聚合物的抗冲击性能，并发现随着冲击速度的提高，材料的能量吸收效果越好。Fan等[17]利用SHPB技术测试了一种聚合物(Clear Flex 75) 在动态压缩下的力学性能，并采用高速摄像机记录了材料的变形过程。针对轻质聚合物材料抗冲击机理研究主要集中在探究材料在冲击载荷下内部微纳米级颗粒结构演化。当前比较认可的演化模型有3种：1)早期Hoffman提出的有序—无序转变(ODT) 模型[18]，Hoffman认为材料内部颗粒在冲击载荷下从有序排列的层状结构转变为无序排列，从而增加了颗粒之间的拖拽力；2)粒子团簇模型，认为内部颗粒在剪应力作用下形成团簇并导致颗粒间相互作用力增大[19-20];3)阻塞转变模型[21]，该模型提出冲击载荷使得材料内部形成了一个颗粒压缩的第2相，这一相逐渐沿加载方向传播并将液态结构转变为瞬时的固态结构。

目前，在冲击硬化过程中从材料的应力状态分析以及力学角度解释抗冲击机理相关研究还比较缺乏。鉴于材料在冲击载荷作用下处于复杂应力状态，单一的动态压缩力学行为难以全面地反映材料的抗冲击性能，且诱导材料发生冲击硬化现象的驱动力并不明确。因此，研究不同应力状态在抗冲击过程中起到的作用十分必要。本文以一种硼酸改性PDMS(PBDMS)添加二氧化硅颗粒的聚合物复合材料(PBDMS-silica)作为载体，测试材料准静态、动态压缩力学行为及抗冲击性能；结合有限元软件ABAQUS分析PBDMS-silica在冲击过程中不同应力状态所起的作用。运用高速摄像机拍摄材料在动态加载下的变形过程，结合数字图像相关(DIC)技术计算试样变形场的演化；进一步参考破坏试样断面形态，分析材料抗冲击性能机理。

1 试验方法

1.1 材料制备与试样尺寸

PBDMS-silica制备过程为：首先将硼酸(质量分数5%)与PDMS及硅油充分混合于烧杯中，然后将一定分数的二氧化硅颗粒加入反应体系；将烧杯中混合物加热到453 K保持恒温，进行3 h搅拌，保证各组成充分混合；搅拌后将混合物置于干燥器中自然冷却即得到目标材料。本文采用了两种二氧化硅质量分数分别为17%和30%的PBDMS-silica，分别以Silica-17%、Silica-30%简化表示。

试验采用圆柱形试样。将适量材料按压进入半开的铝合金模具，压实后打开模具即得到圆柱形试样(见图1(a))。对于准静态压缩试验，试样尺寸为φ10 mm×6 mm；动态压缩试样尺寸为φ10 mm×3 mm；冲击试验试样尺寸为φ10 mm×10 mm.

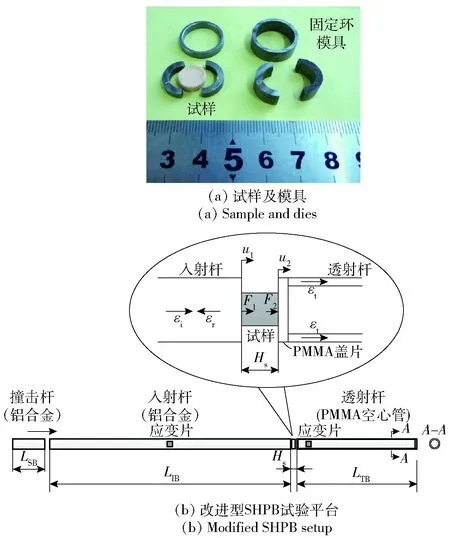
图1 动态试验示意图Fig.1 Illustration of dynamic compression testing

1.2 准静态和动态压缩试验

准静态压缩试验采用美国 INSTRON公司产5848试验机，分别测试Silica-17%和Silica-30%在应变率10-3s-1、 10-2s-1、 10-1s-1下的力学响应。对于软材料的动态力学性能测试采用改进的SHPB试验技术。由于材料波阻抗较小，采用传统的钢杆进行试验难以采集到从试样透过的透射信号，需要对传统的SHPB平台进行相应改进[9, 17, 22-26]。本文试验采用了Miao等[27]提出的SHPB改进方案(见图1(b))。在此方案中，采用铝合金杆作为撞击杆和入射杆(φ15 mm)；选用聚甲基丙烯酸甲酯(PMMA)空心管(外径φ15 mm，内径φ11 mm)作为透射杆，并在空心管端覆盖相同材料的盖片。入射杆应变片粘贴在入射杆中心位置；透射杆应变片粘贴在距杆端30 mm (2倍PMMA管外径)位置，同时避免黏弹性杆弥散效应[28]和应力不均匀性对透射波的影响。基于一维弹性应力波理论，改进SHPB试验平台计算材料应力- 应变关系[27]为

式中：Hs为试样厚度；Ds为试样直径；DTo、DTi分别为透射杆外径、内径；ETB为透射杆弹性模量；cIB、cTB分别为入射杆、透射杆波速；εi、εr、εt分别为入射、反射、透射应变。

动态压缩试验平均应变率分别为800 s-1、1 500 s-1和3 500 s-1，试样尺寸为φ10 mm×3 mm. 对于波阻抗较低的材料，试样长径比保持在0.25～0.50之间能够有效减小波的衰减，并能够尽快实现入射杆、透射杆两端应力平衡[29]。

1.3 金属杆冲击试验

基于SHPB试验平台(见图2)，将试样(φ10 mm×10 mm)置于铝合金支撑杆一端，选用直径小于试样直径的铝合金杆(φ5 mm×300 mm)作为撞击杆；撞击杆由空气炮推动，直接撞击试样表面。试验中，通过高速摄像机拍摄撞击杆的运动过程，并测算出撞击杆从撞击前到撞击后回弹过程中速度随时间变化趋势。分别测试在不同初始速度下(1～6 m/s)撞击杆速度变化，并根据撞击杆回弹的加速度衡量材料的抗冲击性能。

图2 金属杆冲击试验图示Fig.2 Illustration of impact experiment

2 试验结果

2.1 PBDMS-silica在准静态/动态压缩力学响应

图3(a)为试验中通过应变片采集到的入射杆、透射杆上应力波传播的电信号。图3(b)为Silica-17%在1 500 s-1应变率下的应力- 应变曲线和实时应变率- 应变曲线。其中实时应变率- 应变曲线显示试验过程中保持基本恒定的应变率加载。

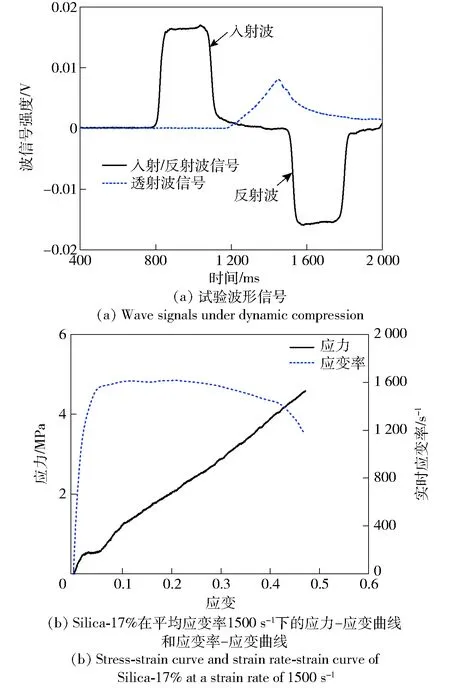
图3 动态试验典型曲线Fig.3 Typical experimental curves under dynamic compression

PBDMS-silica准静态、动态压缩的力学性能如图4所示。在相同的应变率下，Silica-30%的强度均高于Silica-17%. 在准静态压缩载荷作用下，材料首先产生弹性变形，随后进入稳定的应变硬化阶段(见图4(a))。材料的动态应力- 应变曲线在初始阶段出现小幅的应力跌落，随后保持接近直线的趋势(见图4(b))。材料在准静态下强度为千帕量级，而在动态下达到兆帕量级，这表明材料在准静态下为黏性流动状态，而在动态压缩下表现出固体状态。在黏性流动状态下，材料的压缩响应有明显的应变率效应，而在固体状态下，材料应变率敏感性并不明显。

图4 Silica-17%与Silica-30%的应力- 应变曲线Fig.4 Stress-strain curves of Silica-17% and Silica-30%

2.2 PBDMS-silica冲击载荷响应

通过测量冲击Silica-17%与Silica-30%过程中金属杆的速度变化，计算出撞击杆的回弹加速度，从而反映PBDMS-silica的抗冲击性能。如图5(a)和图5(b)所示，金属杆受到空气炮驱动后，以一定初速度撞击试样表面随即开始减速。受到PBDMS-silica抵抗减速后，金属杆速度迅速降为0 m/s，并开始加速回弹，最终以一个恒定速度(小于峰值回弹速度)与试样脱离。当初始速度大于一定值后，试样受到冲击将发生破坏，试验中PBDMS-silica表现出明显的抗冲击特性。图5(c)统计了金属杆以不同初速度冲击Silica-17%与Silica-30%的峰值加速度和最大压缩变形量。在二氧化硅含量一定的情况下，随着金属杆冲击初速度增大，PBDMS-silica将会产生更大的压缩变形，且为金属杆的减速过程提供了更大的加速度。这说明PBDMS-silica的抗冲击特性在一定初速度范围内随应变率的提高逐渐增强。在相同初速度冲击下，Silica-30%试样比Silica-17%提供了更大的加速度，且Silica-30%能够在更小的压缩变形下实现撞击杆的回弹，这说明PBDMS-silica的抗冲击特性随颗粒含量的提高而增强。这与材料动态压缩强度随颗粒含量增强的趋势相对应(见图4)。因此，材料的抗冲击性能在一定范围内随冲击速度和颗粒含量的提高而增强。

3 冲击过程有限元仿真

运用有限元软件ABAQUS 进一步分析冲击过程中材料应力状态变化历程。首先建立与冲击试验材料、尺寸相同的有限元模型(见图6)。根据高速摄影结果，支撑杆(见图2)在冲击过程中的位移不明显。为简化模型，在有限元仿真中将试样未与冲击杆接触端部的边界条件设置为固支。冲击杆材料采用线弹性本构模型，试样材料采用超弹性Mooney-Rivilin本构模型[30]。Mooney-Rivilin本构模型以应变势能函数W描述材料性能：

图6 冲击试验有限元模型Fig.6 Finite element model for impact testing

通过有限元方法，进一步分析PBDMS-silica在抗冲击过程中材料受到的应力状态。图7为Silica-17%在受到一定初速度 (v=5 m/s)冲击时，峰值正应力和剪应力的分布。根据图7(a)，正应力峰值达到1.2 MPa，这与冲击试验中达到峰值加速度时所对应的压强接近。在冲击区域(如图7(a)白色虚线圆圈)下方，形成了圆锥形的应力集中区域，剪应力则集中分布在冲击区域的边缘(见图7(b))，这表明材料在冲击过程中处于压- 剪耦合的复杂应力状态。图8统计了初速度v为1～5 m/s时，PBDMS-silica受冲击区域最大正应力、平均正应力和最大剪应力的变化趋势。随着初速度的提高，正应力响应逐渐趋向平稳，而剪应力一直呈上升趋势，说明随着冲击速度提高，剪力在抗冲击过程中所起作用逐渐上升。

4 结果分析及讨论

4.1 PBDMS-silica应变率效应

材料准静态压缩和动态压缩下应力- 应变曲线在趋势和应力水平上有巨大差异。表2统计了silica-17%与silica-30%在应变为0.4时动/静态压缩流变应力。与准静态加载下强度比较，材料在动态压缩加载下应力提高了104～105倍，这与Jiang等[16]报道的一种冲击硬化聚合物的力学性能吻合。这说明随着应变率的提高，尤其是在动态载荷下，PBDMS-silica材料内部发生了相变，即在低应变率下，材料呈黏性流动状态，而在高应变率下转变为固态。根据PBDMS-silica冲击载荷响应，材料的抗冲击特性在一定初速度范围内随应变率的提高逐渐增强，并且随颗粒含量的提高而增强，值得注意的是，材料在动态压缩下并没有表现出应变率效应。这说明动态压缩仅仅触发了材料内部结构相变，正应力作用不是决定抗冲击特性应变率敏感性的因素。

表1 有限元材料模型参数设置

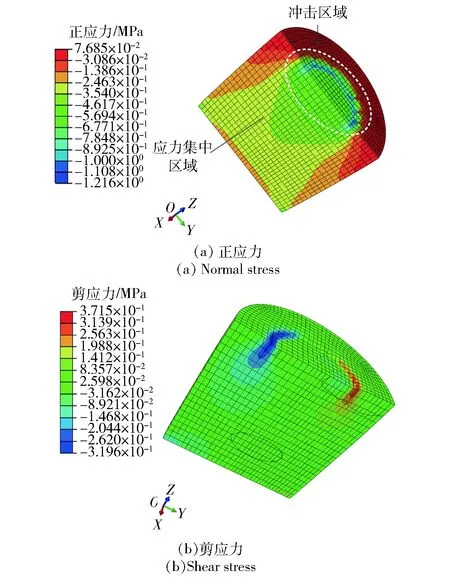
图7 PBDMS-silica受到初速度v=5 m/s金属杆冲击过程中的应力分布云图Fig.7 Distribution of stress of PBDMS-silica under impact loading for an initial velocity v=5 m/s

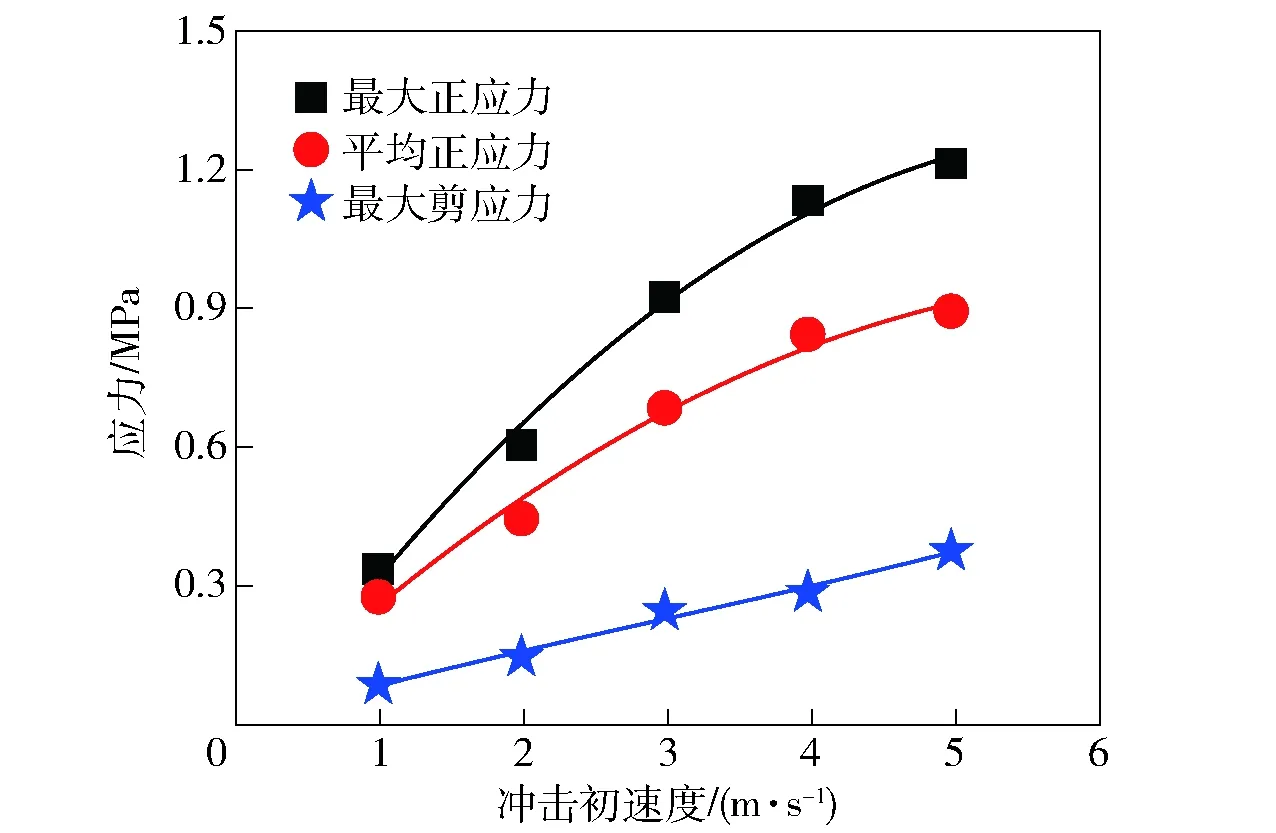
图8 有限元模拟在不同初速度下的材料受冲击区域最大正应力、平均正应力和最大剪应力变化趋势Fig.8 Peak normal stress, average normal stress and peak shear stress versus impact velocity in the impacted region by finite element simulation

4.2 PBDMS-silica抗冲击机理分析

根据动态、静态力学性能及冲击试验结果，PBDMS-silica表现出良好的抗冲击性能。材料在冲击载荷下发生了黏性流动状态到固态的相变，并且抗冲击特性在一定应变率范围内随应变率的提高而增强，这与一些关于剪切增稠液体[31-32]和冲击硬化聚合物[16-17]报道的抗冲击特性类似。然而，这一类材料抗冲击特性的机理还没有一个有力的理论解释。针对材料在冲击过程内部结构转变提出的模型中，受到一定认可的包括有序- 无序转变模型[18]、粒子团簇模型[19-20]和阻塞转变模型[21]。

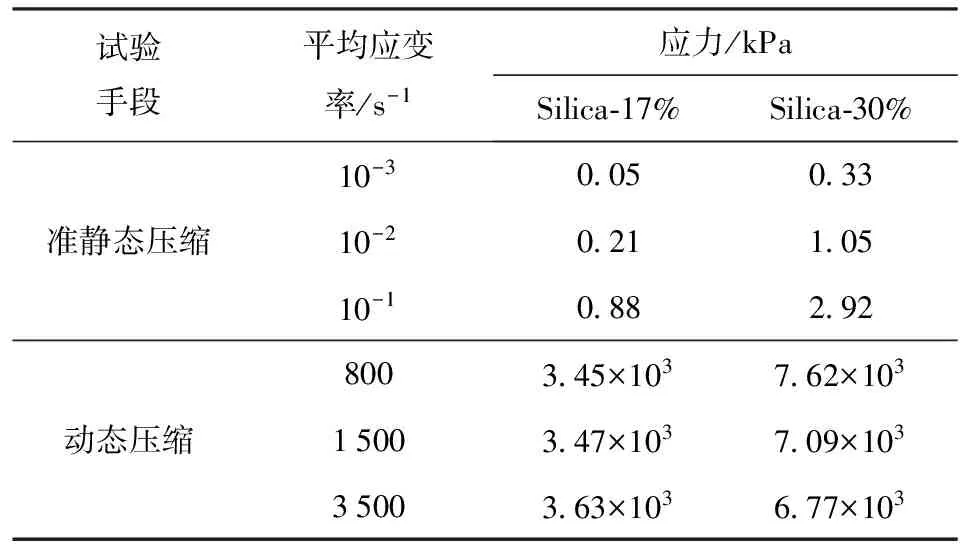
表2 PBDMS-silica在不同平均应变率下的流变应力

为确定材料在抗冲击过程中内部结构转变，以Silica-17%试样作为研究对象，采用高速摄像机记录试样在动态压缩试验中试样的变形过程，并结合DIC技术[33-34]计算试样沿加载方向的变形(见图9(c))。在动态压缩过程中，试样发生非均匀变形，靠近入射杆端的试样产生了明显的压缩变形，而在靠近透射杆端试样变形较小，进而导致试样内部出现阻塞端(见图9(b))。图9(c)显示了连续4帧图像 (frame10～frame13) 试样沿加载方向的变形呈非均匀分布，并在某一个位置出现变形趋势的拐点。对于某一时刻(如图9(c)中frame12)试样上变形场分布，试样变形在拐点(黑色圆圈)后迅速降低，由此认定拐点即为阻塞端。值得注意的是，阻塞端沿加载方向的位置呈线性移动趋势(见图9(c)中虚线箭头)，表明阻塞端呈匀速运动。Waitukaitis等[35]通过模拟实验验证了阻塞端呈匀速运动，并在一定的颗粒含量分数下仅与加载的初速度有关。以上结果证实了在PBDMS-silica受到冲击载荷时，结构内部发生了阻塞转变。

进一步利用光学显微镜观察PBDMS-silica受到冲击破坏后试样的断面。图10显示，试样破坏区域呈圆锥形，这与有限元分析中正应力集中区域形状一致(见图7(a))。根据Waitukaitis等[36]提出的附加质量模型，当PBDMS-silica受到冲击时，冲击区域前方将产生瞬时的颗粒局部聚集，并触发阻塞转变。阻塞转变区域瞬时表现出固体状态，强度迅速提高104～105倍，使得材料表现出抗冲击特性。随着阻塞端向前移动，阻塞区域逐渐扩大，阻塞区域边缘集中分布的剪力(见图7(b))与区域周围材料通相互作用，并带动呈黏弹性材料区域流动，由此形成附加质量(图10右侧黄色区域)。随着附加质量的增加，材料减速作用进一步增强，使得金属杆冲击速度降为0 m/s，并开始回弹，最终脱离试样。

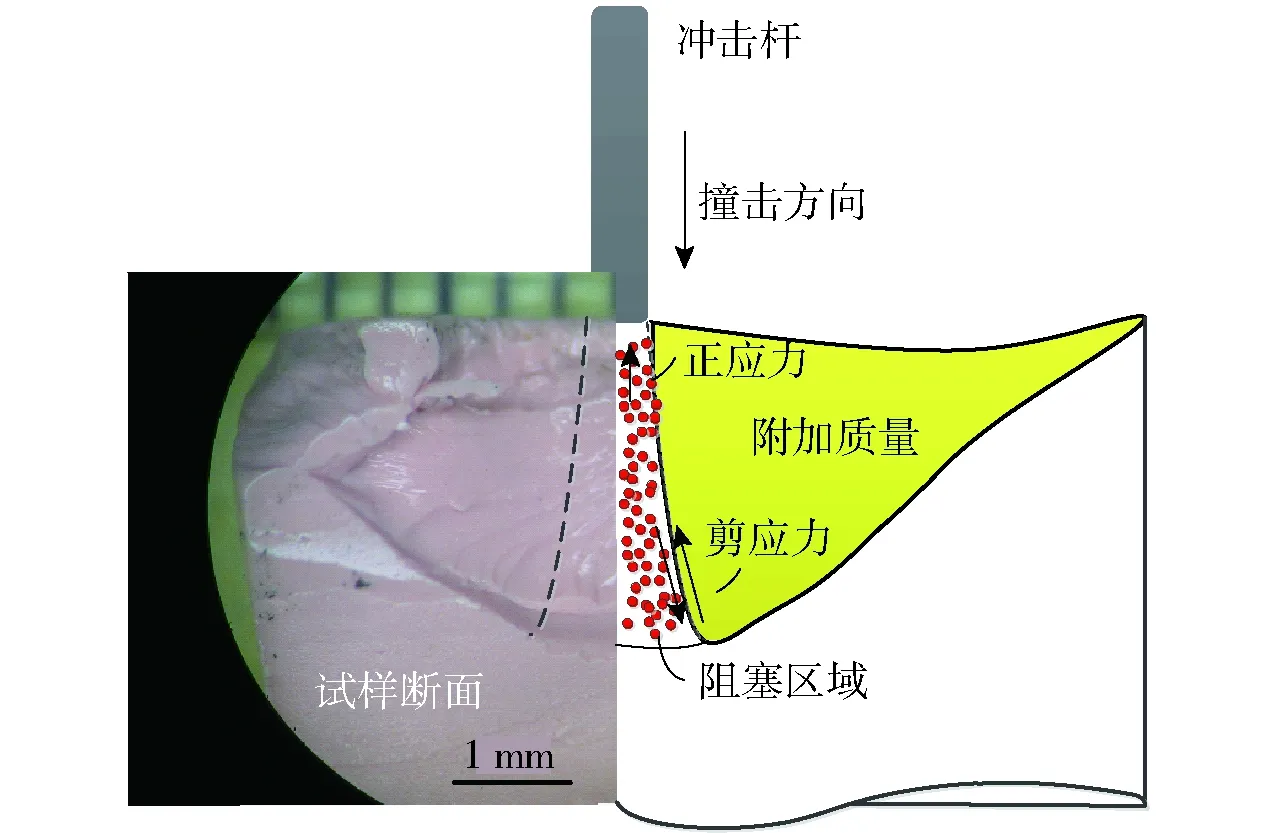
图10 PBDMS-silica冲击破坏试样断面及阻塞转变机理示意Fig.10 Fracture surface of PBDMS-silica after impact loading and illustration of jamming transition

根据有限元分析结果，阻塞区域在冲击过程中处于压力- 剪力耦合的复杂应力状态(见图7)。一般认为，动态压缩下材料强度迅速提高是产生抗冲击性能的决定性因素。但是，剪应力在抗冲击过程中的作用还不明朗。Jiang等[37]考察了剪应力对材料发生连续剪切增稠到非连续剪切增稠转变的作用，提出非连续剪切增稠现象可以看作是剪切引发阻塞转变导致的。Han等[38]通过高速超声波采集试验发现阻塞转变是由剪应力触发的，而不是正应力。根据试验结果和有限元模拟分析，动态压缩响应没有表现出应变率效应，而剪力在抗冲击过程中所起作用随冲击速度提高而增强。认为正应力作用触发阻塞转变，使得材料局部硬化，是材料抗冲击性能的驱动力。但材料抗冲击特性的应变率敏感性则是源于冲击过程中阻塞区域与黏弹性区域剪力的相互作用：随着应变率的提高，阻塞区域与周围区域的相互作用频率提高，导致附加质量增加加快，从而提高了材料对冲击杆的减速效应，同时表现出更加明显的抗冲击性能。

4.3 PBDMS-silica改性方向

根据PBDMS-silica抗冲击性能的机理分析，增大颗粒含量百分比和提高材料动态剪切响应是增强抗冲击性能的有效途径。然而，以聚合物为基体的材料难以无限度地提高二氧化硅颗粒含量。在基体材料和颗粒含量一定的情况下，二氧化硅物理、化学特性将决定材料的剪切响应。例如颗粒形状将直接影响颗粒间相互作用力，进而改变材料的黏性。因此，进一步研究颗粒物理、化学特性对动态剪切响应的影响对改进材料抗冲击性能至关重要。

5 结论

本文研究了一种冲击硬化聚合物复合材料PDBMS-silica的抗冲击性能和材料抗冲击过程中内部结构变化及相应的力学原理。

1) 金属杆撞击试验结果显示，在一定初速度范围内，抗冲击性能随初速度的增大而提高。二氧化硅颗粒含量高的材料表现出更强的抗冲击性能(冲击过程中产生的峰值加速度更大，材料最大压缩变形量更小)。

2) 分别进行准静态压缩试验、基于改进型SHPB平台的动态压缩试验对比材料的动态、静态力学性能。材料在动态加载下强度提高了104～105倍。应变率为1 500～3 500 s-1范围内，材料动态压缩响应下并没有表现出应变率效应。

3) 通过ABAQUS软件模拟冲击试验过程，分析得出材料受冲击区域处于压力- 剪力耦合的复杂应力状态，剪力所起作用随冲击速度提高逐渐增强。

4) 为进一步确定材料抗冲击机理，运用高速摄像机拍摄Silica-17%试样在动态压缩试验中的变形过程，结合DIC技术计算试样沿加载方向变形场。冲击过程中，材料受到冲击区域前方将产生瞬时的颗粒局部聚集并触发阻塞转变，使得材料内部阻塞区域形成固体状态，阻塞区域流变应力迅速提高产生抵抗进一步冲击的正应力；同时阻塞区域通过剪应力与周围黏弹性区域相互作用，加快减速过程。PBDMS-silica的抗冲击性能来源于动态压缩，而剪应力决定了材料抗冲击特性具有应变率效应，即在一定初速度范围内抗冲击性能随冲击速度增大而提高。

5) 鉴于通过提高颗粒含量百分比来增强PBDMS-silica抗冲击性能的方法发展潜力有限，进一步研究颗粒物理、化学特性对动态剪切响应的影响对改进材料抗冲击性能具有重大意义。

)

[1] Hassan T A, Rangari V K, Jeelani S. Synthesis, processing and characterization of shear thickening fluid (STF) impregnated fabric composites[J]. Materials Science and Engineering: A, 2010, 527(12): 2892-2899.

[2] Srivastava A, Majumdar A, Butola B S. Improving the impact resistance performance of Kevlar fabrics using silica based shear thickening fluid[J]. Materials Science and Engineering: A, 2011, 529(1): 224-229.

[3] 李常胜, 黄献聪, 李焱,等. 软体防弹衣穿透概率的分析[J]. 兵工学报, 2013, 34(1): 20-24.

LI Chang-sheng, HUANG Xian-cong, LI Yan, et al. Study on the probability of perforation for soft body armor [J]. Acta Armamentarii, 2013, 34(1): 20-24. (in Chinese)

[4] Norman J, Wagner J F B. Shear thickening in colloidal dispersions[J]. Physics Today, 2009, 62(10): 27-32.

[5] Ding Z T. Nonlinear and adaptive systems[M]. London, UK:Institution of Engineering and Technology, 2013.

[6] Chen W, Lu F, Cheng M. Tension and compression tests of two polymers under quasi-static and dynamic loading[J]. Polymer Testing, 2002, 21(2): 113-121.

[7] Mulliken A D, Boyce M C. Mechanics of the rate-dependent elastic-plastic deformation of glassy polymers from low to high strain rates [J]. International Journal of Solids and Structures, 2006, 43(5): 1331-1356.

[8] Smith D E, Chu S. Response of flexible polymers to a sudden elongational flow[J]. Science, 1998, 281(5381): 1335-1340.

[9] Song B, Chen W. Dynamic stress equilibration in split Hopkinson pressure bar tests on soft materials[J]. Experimental Mechanics, 2004, 44(3): 300-312.

[10] Liu J , Wu S P, Zou M H, et al. Surface modification of silica and its compounding with polydimethylsiloxane matrix: interaction of modified silica filler with PDMS[J]. Iranian Polymer Journal, 2012, 21(9): 583-589.

[11] 魏化震, 李莹, 孔国强. 石英/低聚倍半硅氧烷改性有机硅透波材料性能研究[J]. 兵工学报, 2015, 36(12): 2350-2357.

WEI Hua-zhen, LI Ying, KONG Guo-qiang. Study of properties of quartz / POSS modified silicone wave-transparent materials[J]. Acta Armamentarii, 2015, 36(12): 2350-2357.(in Chinese)

[12] Bokobza L, Diop A L. Reinforcement of poly(dimethylsiloxane) by sol-gel in situ generated silica and titania particles[J]. Express Polymer Letters, 2010, 4(6): 355-363.

[13] Wu C L, Lin H C, Hsu J S, et al. Static and dynamic mechanical properties of polydimethylsiloxane/carbon nanotube nanocomposites[J]. Thin Solid Films, 2009, 517(17): 4895-4901.

[14] Roché M, Myftiu E, Johnston M C, et al. Dynamic fracture of nonglassy suspensions[J]. Physical Review Letters, 2013, 110(14): 148304.

[15] Von Kann S, Snoeijer J H, Lohse D, et al. Nonmonotonic settling of a sphere in a cornstarch suspension[J]. Physical Review E-Statistical, Nonlinear, and Soft Matter Physics, 2011, 84(6): 060401.

[16] Jiang W, Gong X, Wang S, et al. Strain rate-induced phase transitions in an impact-hardening polymer composite[J]. Applied Physics Letters, 2014, 104(12): 1100.

[17] Fan J T, Weerheijm J, Sluys L J. Dynamic compressive mechanical response of a soft polymer material[J]. Materials and Design, 2015, 79:73-85.

[18] Hoffman R L. Discontinuous and dilatant viscosity behavior in concentrated suspensions. II. Theory and experimental tests[J]. Journal of Colloid and Interface Science, 1974, 46(3): 491-506.

[19] Brady J F, Bossis G. The rheology of concentrated suspensions of spheres in simple shear flow by numerical simulation[J]. Journal of Fluid Mechanics, 1985, 155: 105-129.

[20] Cheng X, Mccoy J H, Israelachvili J N, et al. Imaging the microscopic structure of shear thinning and thickening colloidal suspensions[J]. Science, 2011, 333(6047): 1276.

[21] Liu A J, Nagel S R. The jamming transition and the marginally jammed solid[J]. Annual Review of Condensed Matter Physics, 2010, 1(1):347-369.

[22] Chen W, Lu F, Frew D J, et al. Dynamic compression testing of soft materials[J]. Journal of Applied Mechanics, 2002, 69(3): 214-223.

[23] Lim A S, Lopatnikov S L, Gillespie J R J W. Development of the split-Hopkinson pressure bar technique for viscous fluid characterization[J]. Polymer Testing, 2009, 28(8): 891-900.

[24] Lim A S, Lopatnikov S L, Wagner N J, et al. Investigating the transient response of a shear thickening fluid using the split Hopkinson pressure bar technique[J]. Rheologica Acta, 2010, 49(8): 879-890.

[25] Lomakin E V, Mossakovsky P A, Bragov A M, et al. Investigation of impact resistance of multilayered woven composite barrier impregnated with the shear thickening fluid[J]. Archive of Applied Mechanics, 2011, 81(12): 2007-2020.

[26] 陈鹏, 卢芳云, 覃金贵,等. 含钨活性材料动态压缩力学性能[J]. 兵工学报, 2015, 36(10): 1861-1866.

CHEN Peng, LU Fang-yun, QIN Jin-gui, et al. Dynamic compressive mechanical properties of tungstenic reactive material[J]. Acta Armamentarii, 2015, 36(10): 1861-1866.(in Chinese)

[27] Miao Y G, Li Y L, Deng Q, et al. Investigation on experimental method of low-impedance materials using modified Hopkinson pressure bar[J]. Journal of Beijing Institute of Technology, 2015, 24(2): 269-276.

[28] Aleyaasin M, Harrigan J J. Wave dispersion and attenuation in viscoelastic polymeric bars: analysing the effect of lateral inertia[J]. International Journal of Mechanical Sciences, 2010, 52(5): 754-757.

[29] Chen W, Zhang B, Forrestal M J. A split Hopkinson bar technique for low-impedance materials[J]. Experimental Mechanics, 1999, 39(2): 81-85.

[30] 李东泽, 郭笑楠, 颜卓程,等. 基于Abaqus的PDMS基底有限元分析[J]. 电子元件与材料, 2015(11): 57-60.

LI Dong-ze, GUO Xiao-nan, YAN Zhuo-cheng, et al. Finite element analysis of PDMS substrate based on Abaqus[J]. Electronic Components and Materials, 2015(11): 57-60. (in Chinese)

[31] Jiang W F, Gong X L, Xuan S H, et al. Stress pulse attenuation in shear thickening fluid[J]. Applied Physics Letters, 2013, 102(10): 101901-1-101901-5.

[32] Lim A S, Lopatnikov S L, Wagner N J, et al. An experimental investigation into the kinematics of a concentrated hard-sphere colloidal suspension during Hopkinson bar evaluation at high stresses[J]. Journal of Non-Newtonian Fluid Mechanics, 2010, 165(19/20): 1342-1350.

[33] Liu J G, Saletti D, Pattofatto S, et al. Impact testing of polymeric foam using Hopkinson bars and digital image analysis[J]. Polymer Testing, 2014, 36:101-109.

[34] Nunes L C S. Shear modulus estimation of the polymer polydimethylsiloxane (PDMS) using digital image correlation[J]. Materials & Design, 2010, 31(1): 583-588.

[35] Waitukaitis S R, Roth L K, Vitelli V, et al. Dynamic jamming fronts[J]. Europhysics Letters, 2013, 102(4): 44001.

[36] Waitukaitis S R, Jaeger H M. Impact-activated solidification of dense suspensions via dynamic jamming fronts[J]. Nature, 2012, 487(7406): 205-209.

[37] Jiang W F, Xuan S H, Gong X L. The role of shear in the transition from continuous shear thickening to discontinuous shear thickening[J]. Applied Physics Letters, 2015, 106(15): 151902.

[38] Han E, Peters I R, Jaeger H M. High-speed ultrasound imaging in dense suspensions reveals impact-activated solidification due to dynamic shear jamming[J]. Nature Communications, 2016, 7: 12243.