基于路面识别的汽车稳定系统滑模控制∗

王其东，刘 伟，陈无畏，汪洪波，黄 鹤

（1.合肥工业大学汽车与交通工程学院，合肥 230009；2.安徽理工大学机械工程学院，淮南 232001）

前言

汽车电子稳定系统(electronic stability program，ESP)是继汽车防抱死系统(ABS)和牵引力控制系统(TCS)之后汽车主动安全控制技术的一次里程碑式的跨越提升。目前汽车稳定控制系统主要通过3种方式实现对汽车的稳定性控制:调整转向角、调整垂向载荷和调整驱动制动力[1]。调整转向角进行稳定性控制，适合车轮处于线性区域的汽车；调整垂向载荷进行稳定性控制，适合装有主动悬架的汽车，且只有在很大的侧向加速度或侧倾角时才有效；随着ABS和TCS的发展，通过差动制动或驱动产生附加横摆力矩，是目前控制系统多采用的控制方法[2－4]。

汽车稳定性控制系统研究中的核心内容是系统的控制策略和结构。国内外在此方面进行了深入的研究，文献[5]中应用混合灵敏度控制理论，通过合理选取加权函数，设计了基于模型的反馈控制器，将其离散化后，采用适当的最小化技术实现了其稳定性控制，但加权函数的计算较为复杂，且稳定性要求较高；文献[6]中采用神经网络预测方法，提高了汽车的横摆暂态性能，但神经网络内部模型结构的确定较为困难；文献[7]中分析了ESP系统在低附条件下控制目标的选择机理，开发了低附着路面汽车稳定控制器，但仅针对低附着这一种路面情况，而控制系统主要通过调节轮胎与路面之间的作用力，路面与轮胎之间力的传递受路面附着系数的制约，因此汽车主动安全控制策略的优劣很大程度上取决于能否充分利用当前路面附着系数。

当汽车在高附着路面行驶时，质心侧偏角较小，可用横摆角速度表征汽车的状态。但当汽车在低附着路面行驶时，汽车易发生侧滑，此时汽车质心侧偏角迅速增大，轮胎侧向力逐渐增大并达到饱和，使横摆力矩与侧向力趋于恒定值，此时驾驶员几乎很难通过改变转向盘转角来改变横摆力矩，汽车丧失转向稳定性，要想控制汽车的稳定性变得很难[8]。因此，在低附着路面上更应严格限制质心侧偏角，才能保证汽车的稳定性。而当汽车在中等附着路面行驶时，汽车的稳定性有时受限于过大的横摆角速度，有时又取决于过大的质心侧偏角，故可通过联合协调控制，实时调节控制参数，通过两个控制变量实现控制参数的最佳匹配，以适应不同行驶工况下汽车稳定性控制的要求。但现有的控制算法很少考虑路面条件的影响，通常将路面附着系数设为常量，算法只能在某种特定路面下获得较好的控制效果，无法实现对不同路面条件的动态自适应。因此本文中采用卡尔曼滤波和递归最小二乘法相结合的方法对路面附着系数进行估算；在此基础上，基于滑模控制理论采用指数趋近律分别设计了横摆角速度滑模控制器、质心侧偏角滑模控制器和两者的联合协调控制，并选取典型路面工况分别进行Matlab/Simulink-Car-Sim联合仿真和硬件在环试验，验证所提出控制策略的有效性。

1 汽车动力学建模

1.1 整车动力学模型

CarSim软件中的汽车模型是一个27自由度的高精度参数化整车动力学模型，将7大子系统(车身、空气动力学、动力系、制动系、转向系、轮胎和悬架)的特性都包括在内。根据研究需要，保留Car-Sim整车模型的主体，仅对动力系统、制动系统和转向系统模型做适当修改，并嵌入自行设计搭建的控制器模型。而对其他子系统仅修改部分参数值，从而完成整车动力学模型的建立。

1.2 线性2自由度参考模型

当汽车的侧向加速度小于0.4g，轮胎的侧偏特性处于线性范围内，线性2自由度汽车模型可很好地表征汽车的理想行驶状态，因此可用来计算汽车期望的横摆角速度和质心侧偏角。2自由度汽车运动微分方程为

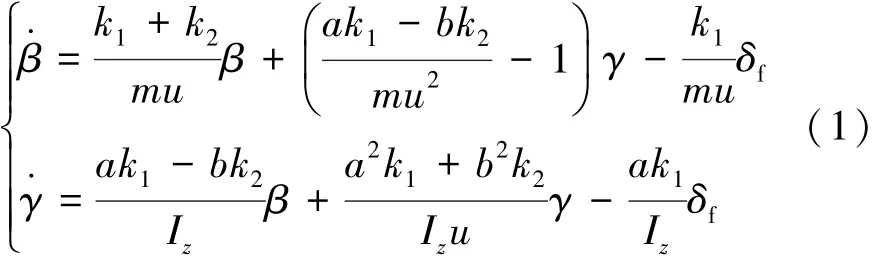
式中:β为质心侧偏角；Iz为汽车绕z轴转动惯量；γ为横摆角速度；k1和k2分别为前、后轮胎的总侧偏刚度；u为汽车纵向车速；δf为前轮转角；a和b分别为质心至前、后轴的距离；m为汽车质量。

当汽车进入稳态时，横摆角速度γ和质心侧偏角β均为定值，此时β·＝0，γ·＝0，由式(1)可得期望的横摆角速度和质心侧偏角为，是表征汽车稳态响应的重要参数。

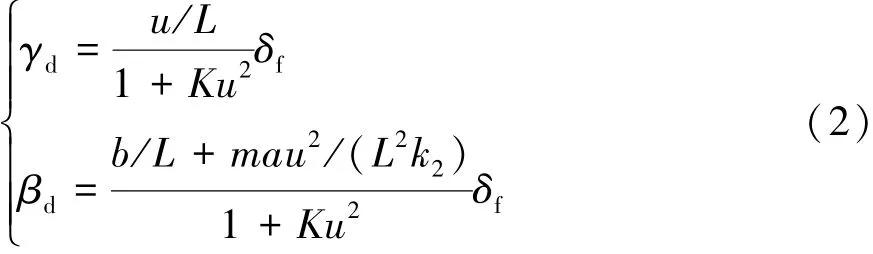
由于汽车的横向加速度ay不能超过轮胎与路面的最大附着系数μ所决定的加速度，即ay≤μg，故理想的横摆角速度和质心侧偏角也将受到限制。稳态时汽车横向加速度为

式中:γd为期望横摆角速度；βd为期望质心侧偏角；L为轴距，L＝a＋b；K为汽车稳定性因数，K＝

式中R为转弯半径。这样横摆角速度就受式(4)不等式的限制:

因此由路面附着系数μ所确定的最大理想横摆角速度和质心侧偏角为

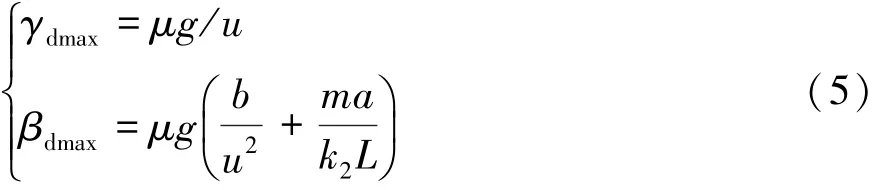
从而式(2)中期望的横摆角速度和质心侧偏角修正为

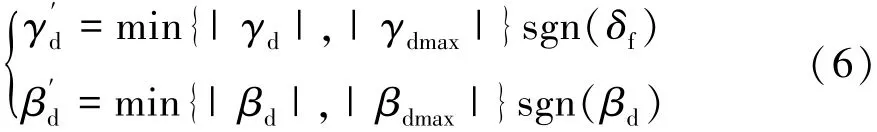
2 路面附着系数识别算法

刷子轮胎模型能比较准确地描述如饱和轮胎力和摩擦椭圆影响等轮胎的非线性特征且求解参数少于魔术公式等模型[9]，本文中采用纵滑侧偏组合刷子轮胎模型进行路面附着系数识别，识别框图如图1所示。

图1 路面识别结构框图

图中:Fx和Fy分别为轮胎的纵向力和侧向力，可利用卡尔曼滤波方法进行估算[10]；Fz为轮胎的垂向载荷；Td为轮胎的驱动力矩；Tb为轮胎的制动力矩；α为轮胎的侧偏角；κ为车轮滑动率。

刷子轮胎模型公式为

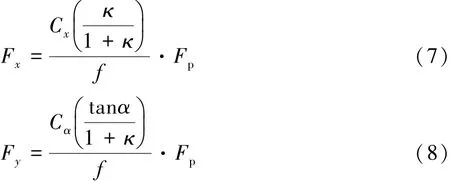
其中:

式中:Cx为轮胎纵滑刚度；Cα为轮胎侧偏刚度；r为车轮滚动半径；vω为轮心处的纵向速度。刷子轮胎模型需要辨识的参数包括 Cx，Cα和 μ，根据文献[10]可知，Cx，Cα与轮胎尺寸、胎面宽度、充气压力和负载等因素有关，且在短时间内变化很小，可近似看作定值。而路面附着系数μ可采用递归最小二乘法进行估算。

首先，非线性的刷子轮胎模型可被写成如下的形式:

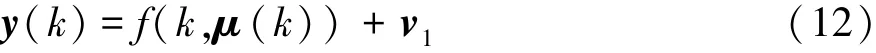
式中:y为轮胎力的测量值，由卡尔曼滤波获得，即 y ＝ [Fx，Fy]T；f(k，μ(k)) 为刷子轮胎模型的表达式，其中μ(k)为轮胎模型参数；v1为相应的测量噪声。

为满足最小二乘法要求，将y(k)线性化，式(12)可近似写为

其中

定义变量h(k)为

将式(14)代入式(15)中，可得

由此得到关于路面附着系数μ的近似线性化表达形式，然后进行递归最小二乘估算。设置递归最小二乘的价值函数为

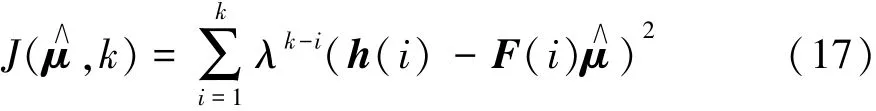
式中λ为遗忘因子。最小二乘法的估算原则是使价值函数的导数为零，即将其值最小化。最小二乘法的估算表达式为

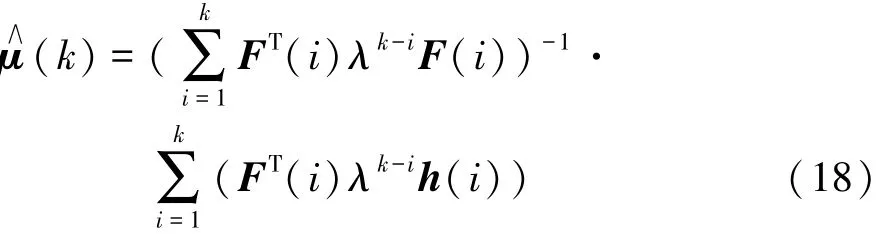
参数向量μ(k)可由新的观测值h(i)进行更新，因此能被在线估算。其中的误差协方差矩阵为

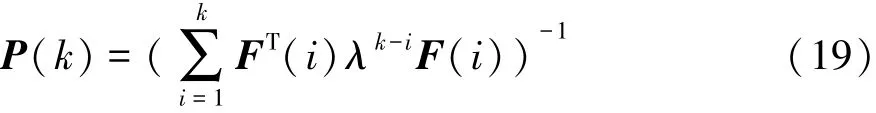
可由Sherman-Morrison方程递归计算:

将式(19)和(20)代入式(18)，并设定状态初值μ(0)和P(0)，则递归最小二乘法的迭代过程为

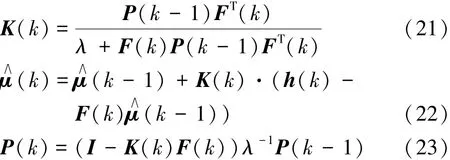
在滑动率很小时，算法可能会出现较大的振荡和不可预估的估算结果[11]。为避免这种错误的估算结果，设置一个滑动率门限κup，估算结果只有在大于滑动率门限时才进行更新，如果低于滑动率门限则保持上一个时刻的估算值不变:

路面附着系数估算算法的灵敏度由设定的滑动率门限决定，若门限值过大，则估算灵敏度不够，估算值不能及时更新，而门限值过小，则滑动率较低时，估算值会出现较大的振荡和不可预估的估算结果，本文中κup取0.08。

3 ESP控制系统设计

3.1 ESP控制系统结构设计

图2为包含上层协调控制器和下层子系统控制器的ESP控制系统结构框图。该系统是一个基于汽车运动状态识别的协调控制器，根据汽车各个运动状态和运动关系，可总结出如下的状态识别流程:首先根据前轮转角、横摆角速度偏差和质心侧偏角偏差来判断汽车是处于不足转向、过度转向还是中性转向；接着根据识别的路面附着系数，选取合适的控制策略。上层状态识别器根据获得的信息，进行分析判断后，实时分配给下层子系统控制器控制参数和控制目标，使汽车在各种路况下都能稳定行驶。下层子系统控制器则根据误差的大小确定所需产生的附加横摆力矩ΔM。由于单轮制动对汽车冲击和运动性能的影响较小，故参考文献[12]选取单轮制动的方法来实现附加横摆力矩的分配。

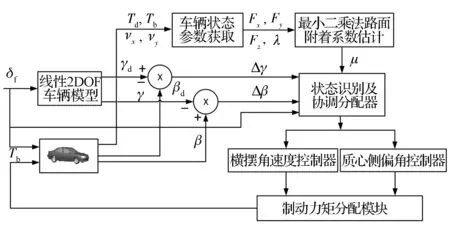
图2 ESP控制系统结构

3.2 上层协调控制器设计

上层协调控制器是一个决策控制器，对下层控制器起决策、监控的作用。它相当于一个选择开关:当汽车正常行驶时，上层协调控制器起到监控下层各控制器的作用，对主要指标(路面附着系数、横摆角速度和质心侧偏角)进行监控；当汽车出现失稳工况时，上层协调控制器发现异常后，对下层控制器发出决策指令，以确定下层子系统所采用的控制策略，其流程图如图3所示。

图3 上层控制器控制流程图

上层协调控制器的控制策略设计如下。

(1)根据文献[13]，确定汽车失稳时横摆角速度准稳定公差带｜Δγ｜＝｜γ －γd｜＝｜c·γd｜和质心侧偏角准稳定公差带｜B1β＋B2β·｜＜1，式中c＝0.165，B1＝ 9.459，B2＝ 2.497。

(2)如果横摆角速度偏差和质心侧偏角偏差在稳定范围内，则ESP系统不工作，上层协调控制器起监控作用，不发出控制指令。

(3)如果横摆角速度偏差和质心侧偏角偏差不在稳定范围内，则上层协调控制器发出决策指令；此时，根据文献[14]，若路面附着系数小于0.35，则选取质心侧偏角控制策略；若路面附着系数在(0.35，0.6]之间，则选取联合控制策略；若路面附着系数大于0.6，则选取横摆角速度控制策略。

3.3 下层子系统控制器设计

以线性2自由度模型为基础，设计考虑控制变量变化率的高阶滑模控制器，从而对整车失稳状态施加附加横摆力矩ΔM。因此，式(1)演变成加入附加横摆力矩的2自由度模型微分方程:

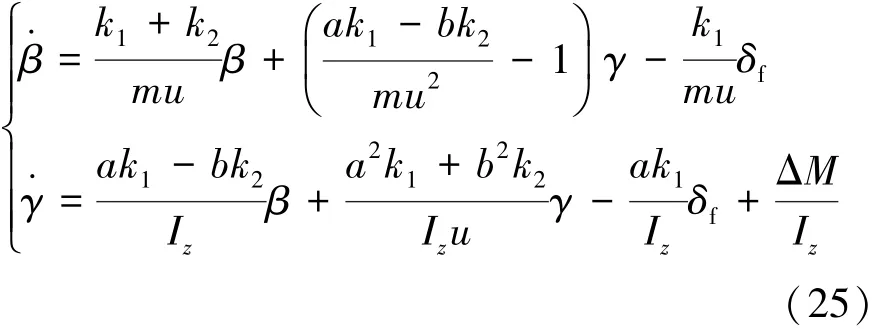
3.3.1 横摆角速度滑模控制器设计

横摆角速度滑模控制器控制面的设计，须使汽车实际横摆角速度跟随期望横摆角速度，保证轮胎始终处于线性特性范围内。因此定义横摆角速度滑模面为

对滑模面s进行1阶求导，并将式(25)代入可得

采用指数趋近律的方法，结合式(27)可得横摆角速度控制的附加横摆力矩ΔMγ:

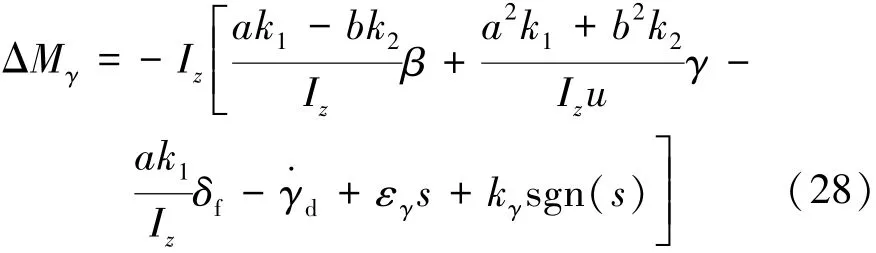
式中:εγ和kγ为横摆角速度控制指数趋近律参数，且 εγ＞ 0，kγ＞ 0。

3.3.2 质心侧偏角滑模控制器设计

质心侧偏角滑模控制器控制面的设计，须使汽车实际质心侧偏角始终跟随期望质心侧偏角，防止汽车侧滑。假设实际值与理想值的误差为零，即:eβ＝β－βd＝0，误差变率＝－定义质心侧偏角滑模面为

对滑模面s进行1阶求导，将式(25)代入可得

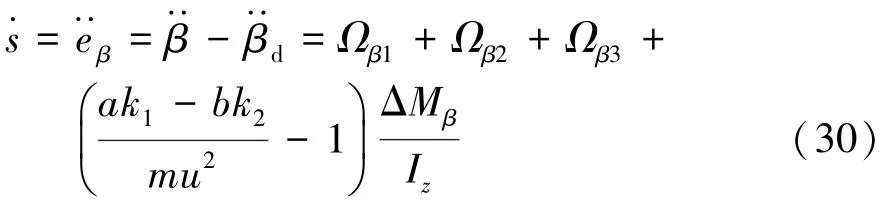
其中

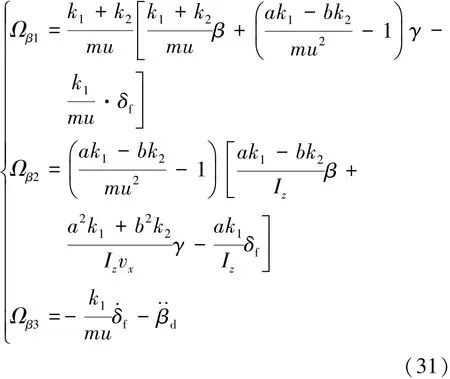
同理，可得质心侧偏角控制的附加横摆力矩ΔMβ:

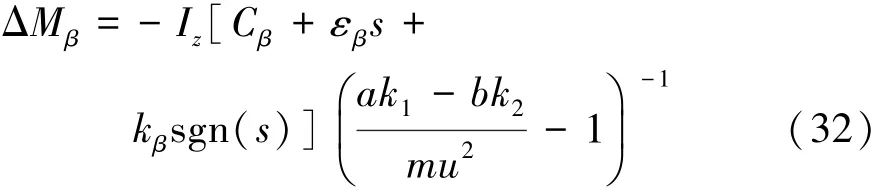
式中:εβ和kβ为质心侧偏角控制指数趋近律参数，且 εβ＞ 0，kβ＞ 0。

在滑模控制器设计中，符号函数sgn(s)的存在使系统出现不连续的开关特性而造成抖振，本文中为削弱或抑制抖振，在控制器的设计中采用饱和函数sat(s/φ)代替符号函数sgn(s)，保证在切换面附近控制输入的光滑连续性[15]。饱和函数为

式中:φ为边界层厚度，取0.05。

3.3.3 横摆角速度和质心侧偏角协调控制

当汽车在中等附着路面行驶时，汽车的稳定性有时受限于过大的横摆角速度，有时又取决于过大的质心侧偏角，必须同时对这2个变量进行控制，这样可以解决单独控制横摆角速度时质心侧偏角过大和单独控制质心侧偏角时不能很好跟踪理想横摆角速度的问题。因此须对横摆角速度和质心侧偏角进行联合控制，实现汽车在各种工况下的稳定行驶。横摆角速度控制器输出的附加横摆力矩ΔMγ和质心侧偏角控制器输出的附加横摆力矩ΔMβ进行加权协调控制，得出最终的附加横摆力矩ΔM:

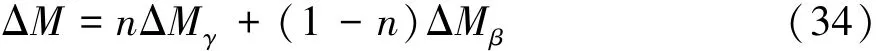
式中n为协调控制加权系数。n的取值由路面附着系数决定:

式中:μ0和μ1为确定的路面附着系数，其值由文献[14]确定。

3.3.4 滑模变结构控制系统稳定性分析

利用李雅普诺夫第二稳定判据对设计的控制系统进行稳定性分析，以横摆角速度为例分析控制系统的稳定性。定义Lyapunov函数为

可得

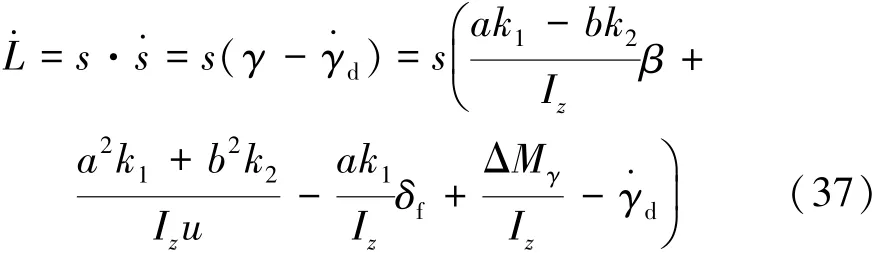
将ΔMγ代入上式可得

因为kγ＞0，所以L·≤0，表明系统稳定。同理可证质心侧偏角控制和联合控制时系统均稳定。

4 仿真分析和试验验证

4.1 仿真分析

为验证所提出控制策略的有效性，在CarSim中建立整车动力学模型并与Matlab/Simulink进行联合仿真，分析比较在不同路面附着系数下所设计的控制器对汽车极限工况的响应特性。整车参数见表1。

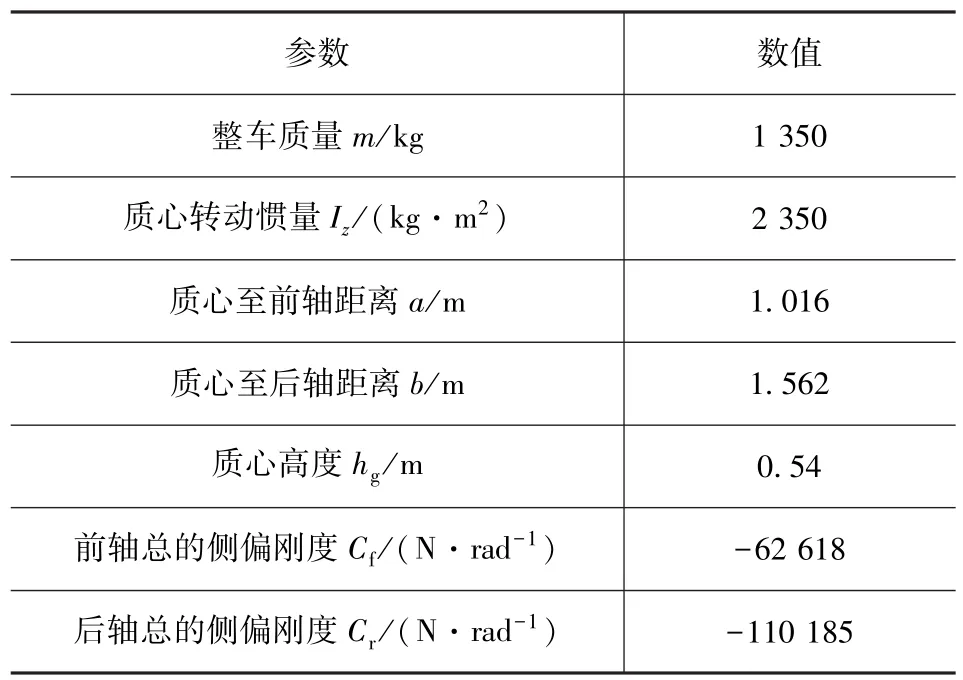
表1 整车参数表

仿真条件:根据 GB/T 30677—2014，采用初始车速 80km/h、幅值 1.5rad(85.95°)、频率为 0.7Hz的正弦信号作为转向盘转角的输入，验证所设计的控制器在对应的路面附着系数下的控制效果，选取典型高、中、低路面附着系数下相同的极限工况进行仿真。

工况1:在CarSim中设定低附着路面的路面附着系数μ＝0.2，汽车在此路面行驶的仿真结果如图4～图6所示。

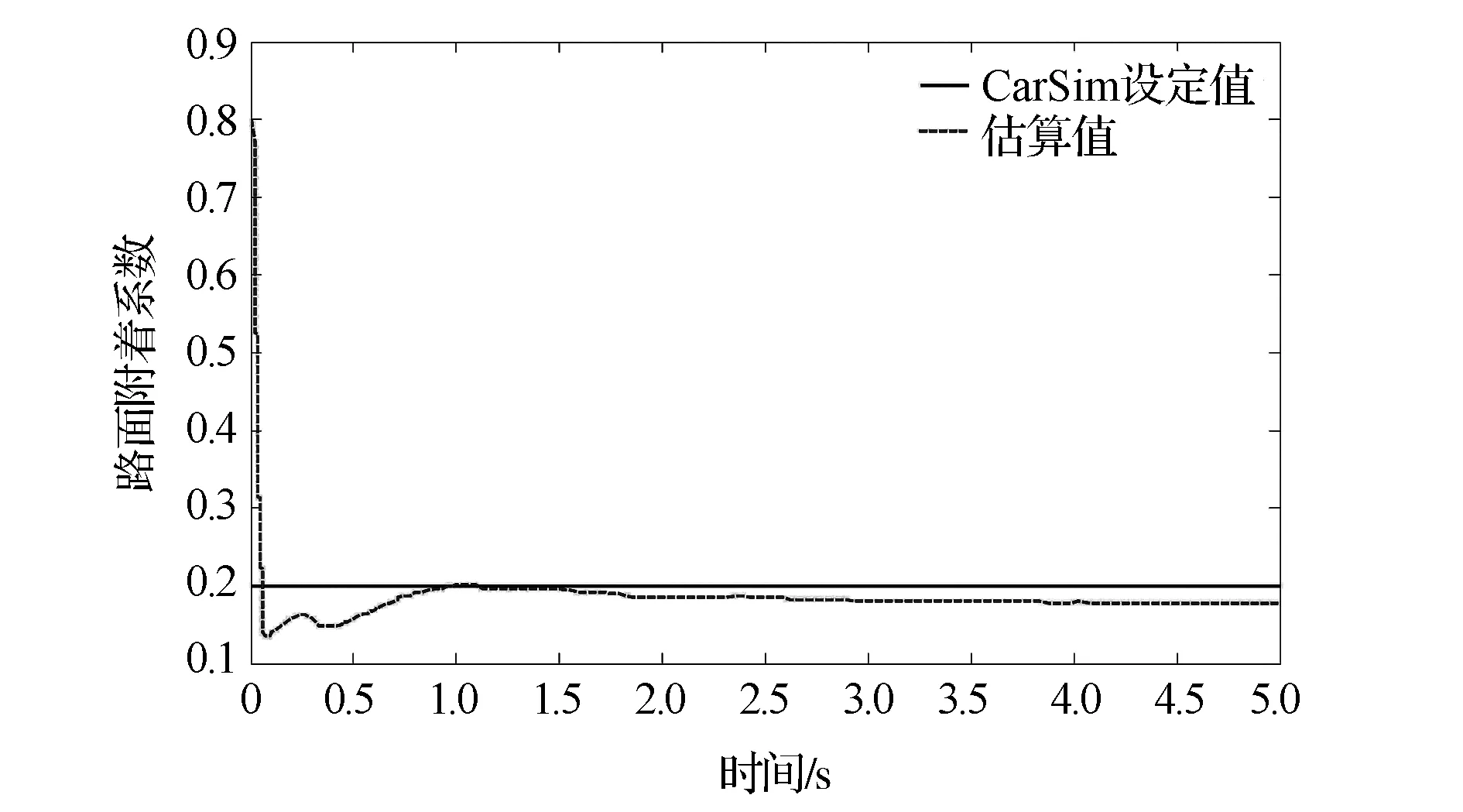
图4 低附着路面附着系数估算

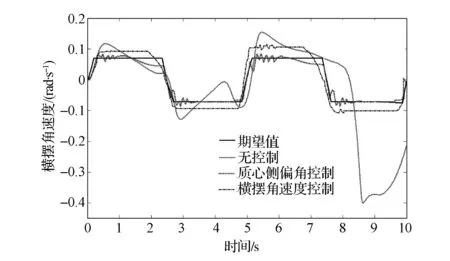
图5 横摆角速度响应曲线

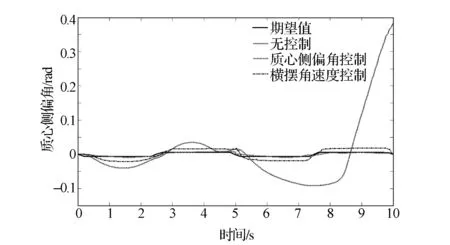
图6 质心侧偏角响应曲线

图4 为采用式(16)估算的路面附着系数值与CarSim给定值的比较，结果显示估算值能够在很短的时间内收敛到0.2附近，表明了所提出的路面附着系数估计算法的正确性。图5和图6分别为横摆角速度和质心侧偏角的响应曲线。可以看出，无控制时，横摆角速度和质心侧偏角出现较大变化，且在8.5s时达到0.4rad，远远超过此附着系数下汽车所允许的最大横摆角速度和质心侧偏角，表明汽车严重失稳并出现侧滑。采取质心侧偏角控制后各项参数均能很好地跟随转向输入的变化而变化，稳定在期望值附近；而采取横摆角速度控制后虽对汽车失稳有一定的控制作用，但偏离期望值较大，综上分析表明，汽车在低附着路面上失稳时，采取质心侧偏角控制比横摆角速度控制效果好。

工况2:在CarSim中设定路面附着系数μ＝0.5，汽车在此中附着路面上行驶的仿真结果如图7～图9所示。

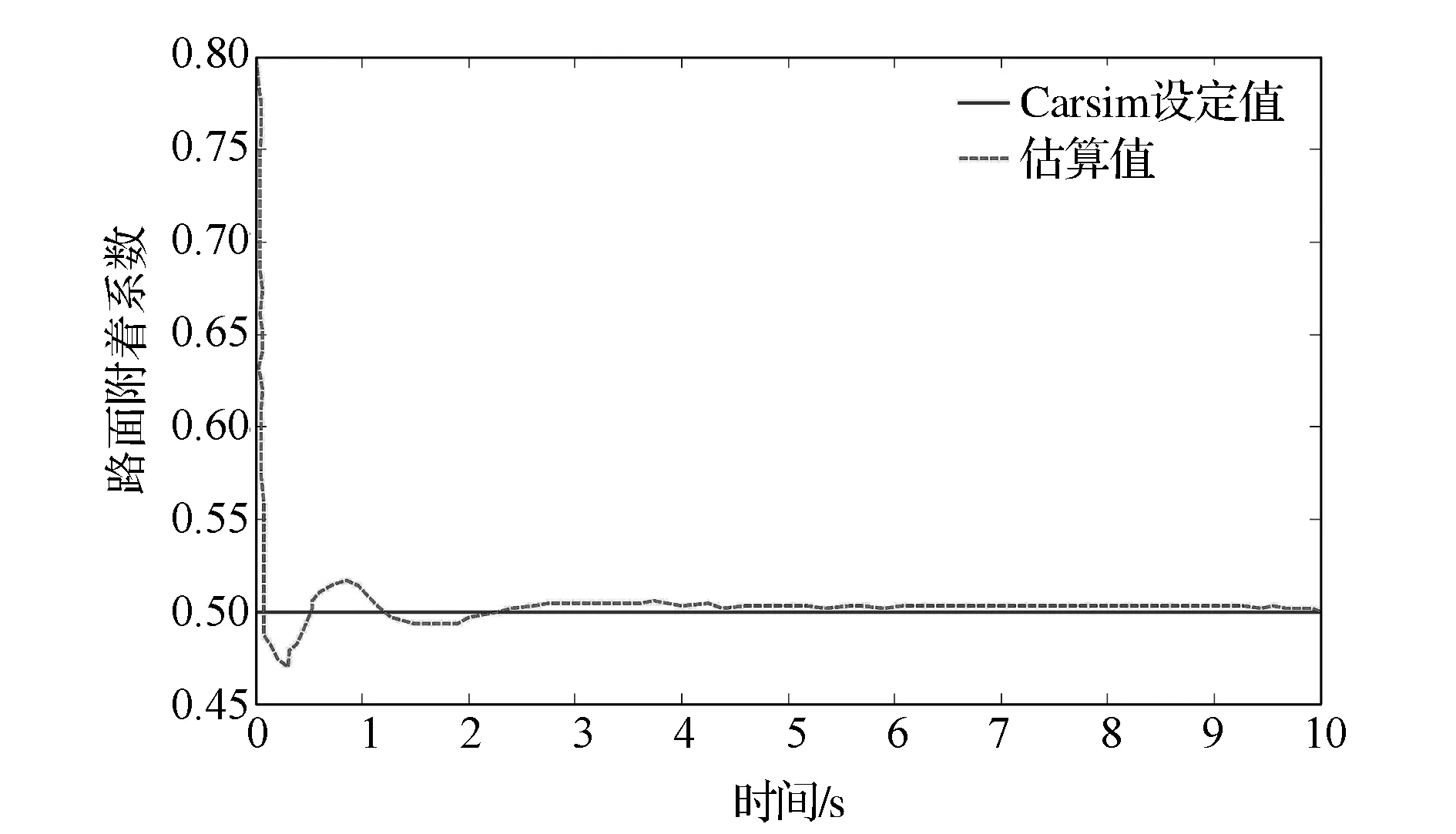
图7 中附着路面附着系数估算

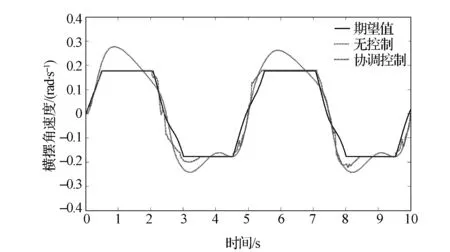
图8 横摆角速度响应曲线

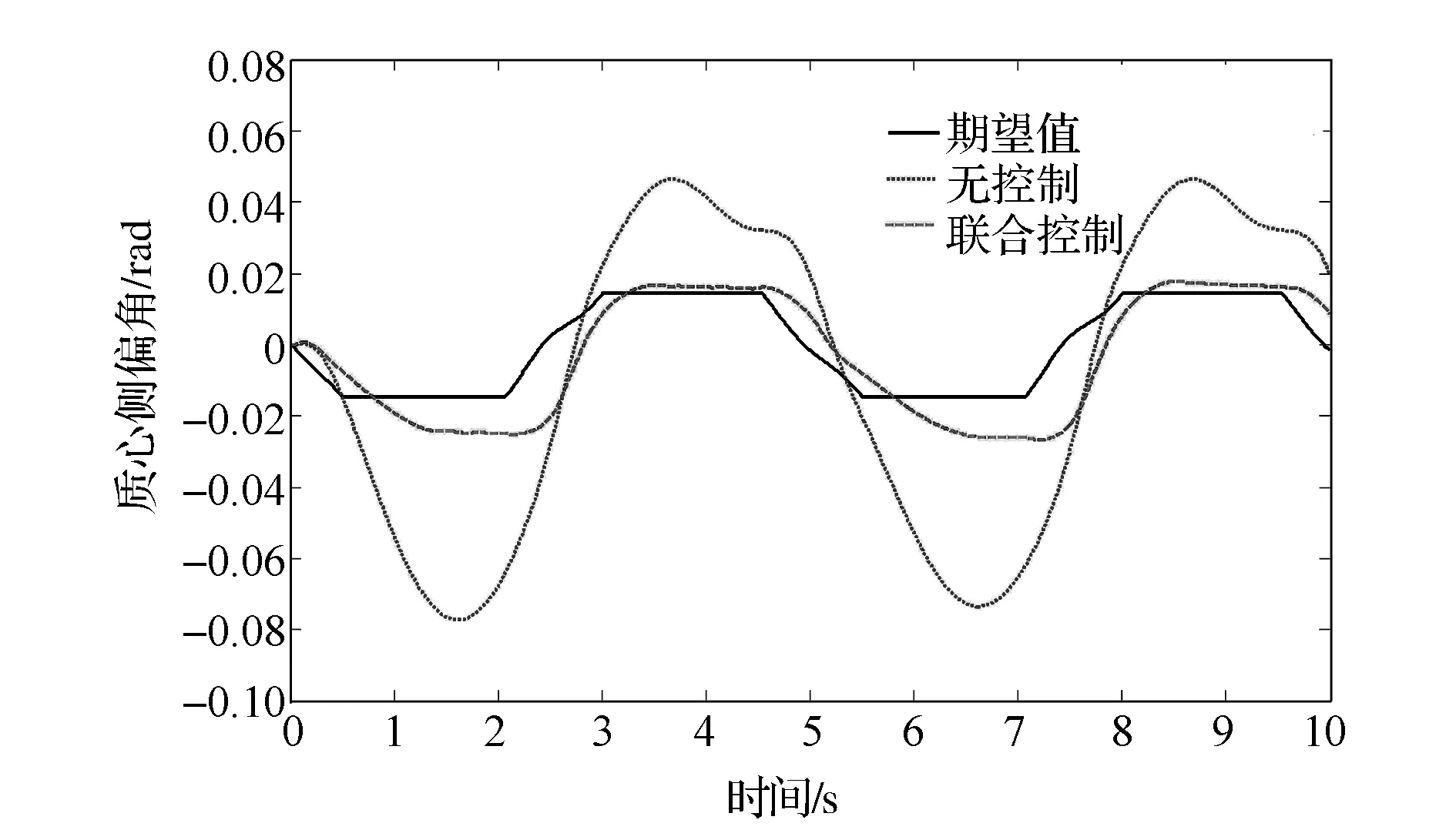
图9 质心侧偏角响应曲线

由图7可见，路面附着系数估算值几乎在2s内收敛到给定值0.5左右，充分证明了该估计算法的有效性。由图8和图9可见，无控制时汽车出现过度转向趋势，且横摆角速度在1s后达到0.3rad，导致汽车不稳定，而施加联合协调控制后，汽车响应能较好地跟踪期望横摆角速度和质心侧偏角。

工况3:在Carsim中设定高附着路面的附着系数μ＝0.85，仿真结果如图10～图12所示。

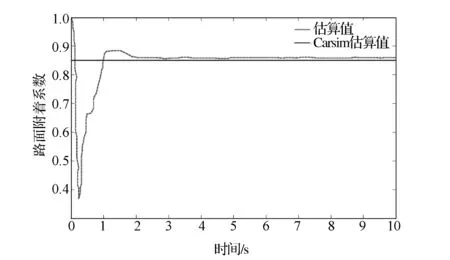
图10 高附着路面附着系数估算

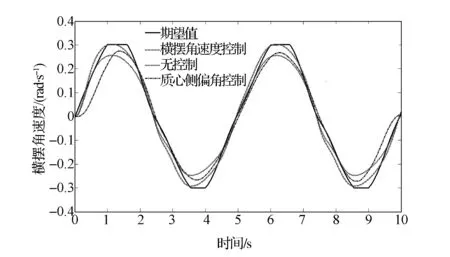
图11 横摆角速度响应曲线

图12 质心侧偏角响应曲线

由图10可见，高附着路面附着系数估算值能迅速收敛到CarSim给定值，充分证明了该估计算法的有效性和正确性。而由图11和图12可见，无控制时汽车出现不足转向，而施加横摆角速度控制后汽车的横摆角速度和质心侧偏角趋近期望值，汽车行驶在稳定范围内，而采取质心侧偏角控制后虽对汽车的不足转向有一定的改善作用，但效果并不明显，说明汽车在高附着路面上失稳主要是由过大的横摆角速度偏差造成的，采取横摆角速度控制比质心侧偏角控制效果好。

以上仿真结果表明了所设计的路面附着系数识别算法的正确性；同时表明了基于路面识别所设计的不同控制器能够很好地保持在对应路面附着系数下的汽车高速行驶稳定性，系统响应迅速。

4.2 硬件在环仿真试验

采用硬件在环仿真试验对提出的控制策略进行验证，试验平台如图13所示。

图13 硬件在环试验平台

该试验台由上位机、下位机、接口系统、控制器和硬件系统5个部分组成。上位机是一台普通PC机，在安装的CarSim软件中建立整车动力学模型，并在LabVIEW软件中编写ESP虚拟控制器程序；下位机是NI公司的PXI8196实时系统，运行上位机建立的整车模型和虚拟的ESP控制器；接口系统起承上启下的作用，一方面将传感器采集到的信号通过PXI实时系统输入到虚拟控制器[16]，另一方面将虚拟控制器控制输出信号发送给控制对象。应用Lab-VIEW进行ESP虚拟控制器设计；硬件系统主要包括转向机构、传感器和执行器等。上位机、下位机、虚拟控制器和液压单元驱动模块四者通过网络互连交互数据，上位机对仿真过程的状态监控通过使用LabVIEW RT提供的网络共享变量技术实现，其它信号通过信号线在硬件平台之间传递，信号流程如图14所示。

硬件在环试验方案:由 NI公司开发的 Lab-VIEW-RT系统，在工控机Windows XP操作界面上运行LabVIEW软件，实现硬件的在线控制、信号的实时采集处理和曲线的显示等功能。硬件在环仿真测试开始前，在CarSim软件内设置车辆参数和试验工况，进行硬件在环仿真试验。

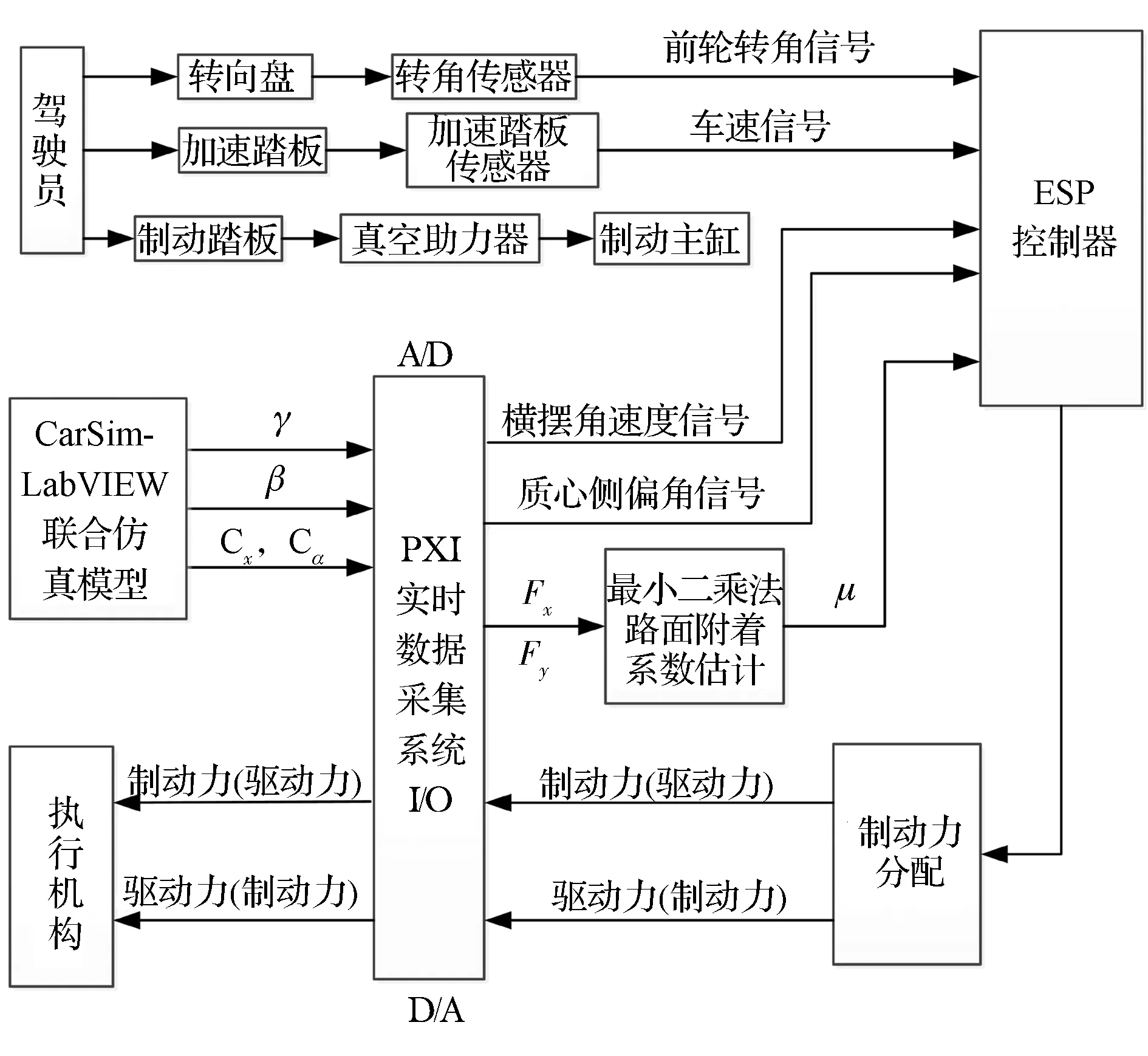
图14 硬件在环试验平台信号流程图

(1) 采用车速 80km/h、幅值 1.5rad(85.95°)、频率为0.7Hz的正弦信号作为转向盘转角输入，设置路面附着系数为0.2，试验结果如图15～图17所示。

图15 路面附着系数估算

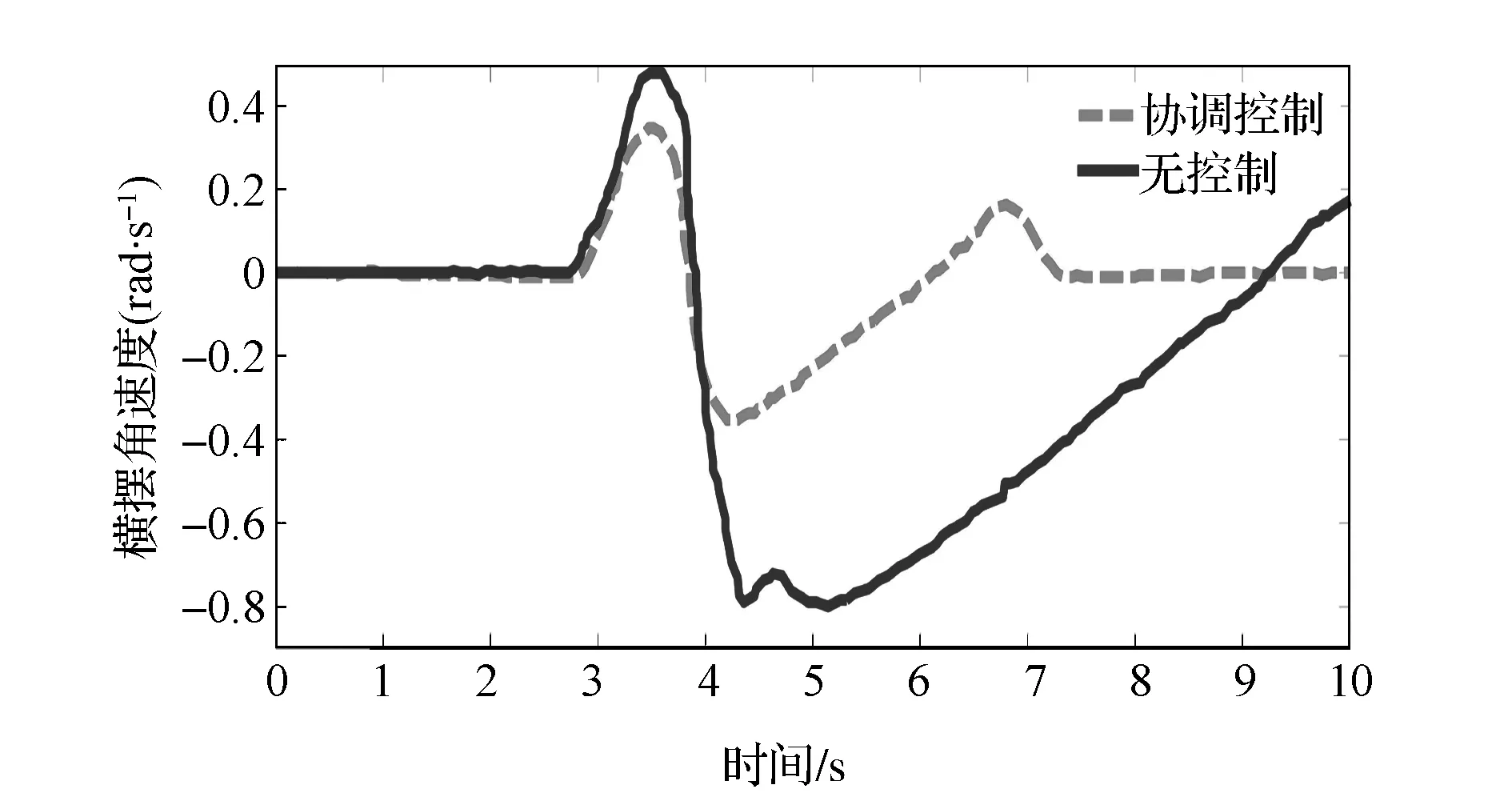
图16 横摆角速度曲线

由图15可见，估算值介于 0.17～0.22之间，最大瞬态误差约为15%，其余时刻的估算误差均在10%以下，可较好地跟随真实值，证明了估算方法可有效地估算出路面附着系数的变化趋势。由图16和图17可见:不加控制时，汽车的横摆角速度和质心侧偏角的最大值已远远超过此路面附着系数所允许的最大值，汽车出现严重的失稳现象；施加控制后横摆角速度和质心侧偏角的幅值迅速减小，且处于稳定范围内。

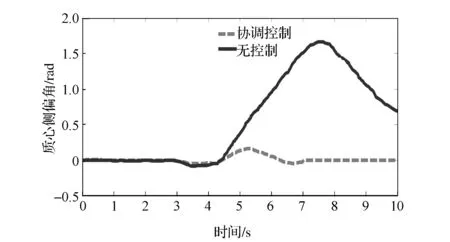
图17 质心侧偏角曲线

(2)采用车速80km/h、幅值1.5rad(85.95°)、频率为0.7Hz的正弦信号作为转向盘转角输入，在0－2.3s时，设置路面附着系数为0.8，在2.3s后的路面附着系数设置为0.4，转向盘转角幅值为1.5rad(85.95°)，试验结果如图18～图20所示。

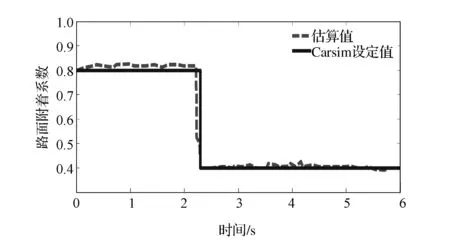
图18 路面附着系数估算

图19 横摆角速度响应曲线

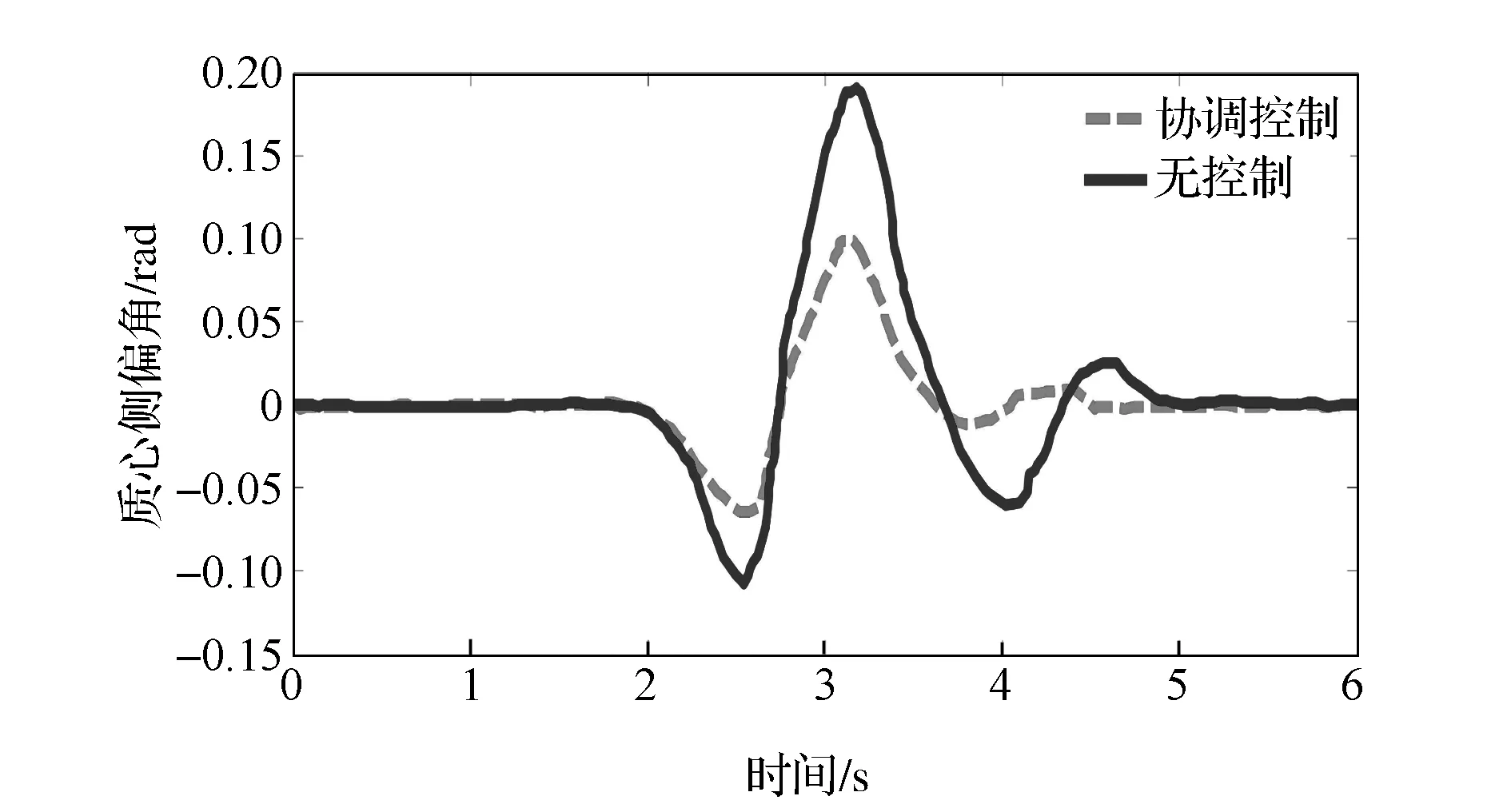
图20 质心侧偏角响应曲线

由图18可见，当路面发生跃变时，估算值可较好地跟随真实值，证明了估算方法可有效地估算出路面附着系数由大到小的变化趋势，算法响应速率较快，估算结果较为准确。值得注意的是，当时间为2.3s时，估算值出现了较大波动，原因是滑移率的变化，之后的估算值趋于稳定，且稳定后的估算误差在3%以内，说明此处的波动对整体估算结果没有较大的影响。由图19和图20可见，采用ESP控制的幅值比未采用的幅值要小，且汽车行驶在稳定范围内。硬件在环仿真试验的结果验证了仿真结果的正确性，表明所提出的控制器能使汽车在不同附着路面上失稳时的汽车横摆角速度和质心侧偏角的幅值得到较明显的降低。

5 结论

(1)路面附着系数对汽车的稳定性具有重要影响，不同路面附着系数下汽车的动力学特性不同，汽车失稳的主要因素也不同。因此，引入路面附着系数识别对简化汽车稳定性控制系统结构，提高控制精度具有重要作用。

(2)采用指数趋近律设计了滑模变结构控制器，采用递归最小二乘法进行路面附着系数估算，将识别的路面附着系数传递给控制器，控制器通过传感器对汽车的运动姿态和驾驶员指令进行监控，当汽车失稳时，对比汽车实际行驶状态与驾驶员期望状态的误差，计算附加横摆力矩，同时根据识别的路面附着系数选取不同的控制策略。

(3)进行了典型工况仿真分析和硬件在环试验，结果验证了所提出的路面附着系数估算算法及ESP控制策略的有效性。试验结果表明，硬件在环试验是ESP控制器控制算法开发、调试和参数匹配的有效手段。

[1] 林程，彭春雷，曹万科.独立驱动电动汽车稳定性的滑模变结构控制[J].汽车工程，2015，37(2):132－138.

[2] 胡延平，陈无畏，刘翔宇，等.基于非线性直接横摆力矩控制的ESP研究[J].汽车工程，2013，35(5):424－429.

[3] 夏长高，李心庆，郑恩瑞.主动横摆控制在车辆横向稳定性中的应用研究[J].机械设计与制造，2015(4):35－38.

[4] 杨鹏飞，熊璐，张康，等.分布式电驱动汽车稳定性控制策略设计与试验[J].机械工程学报，2013，49(24):128－134.

[5] CERONE Vito， MILANESE Mario， REGRUTO Diego.Yaw stability control design through a mixed-sensitivity approach[J].IEEE Transactions on Control Systems Technology， 2009，17(5):1096－1104.

[6] YANG T，SONG D D.Vehicle stability control study based on neural network predictive method[J].Applied Mechanics＆ Materials，2015， 734:295－298.

[7] 李亮，宋健，于良耀，等.低附路面汽车动力学稳定性控制系统控制策略[J].机械工程学报，2008，44(11):229－235.

[8] 徐明法.基于最优滑模控制理论的车辆稳定性控制策略研究[D].长春:吉林大学，2011.

[9] ZHAO J， ZHANG J， ZHU B.Development and verification of the tire/road friction estimation algorithm for antilock braking system[J].Mathematical Problems in Engineering， 2014， 2014.

[10] CHOI M，OH J J，CHOI S B.Linearized recursive least squares methods for teal-time identification of tire-road friction coefficient[J].IEEE Transactions on Vehicular Technology， 2013，62(7):2906－2918.

[11] SAVINKINA E N，SAKHANENKO A I.Enhancement of collision mitigation braking system performance through real-time estimation of tire-road friction coefficient by means of smart tires[J].SAE International Journal of Passenger Cars-Electronic and Electrical Systems， 2014， 18(1):69－77.

[12] LI J，YANG H.Fuzzy logic applied to yaw moment control for vehicle stability[J].Vehicle System Dynamics International Journal of Vehicle Mechanics＆ Mobility，2005，43(10):753－770.

[13] 邱磊.汽车ESP控制系统建模及仿真研究[D].重庆:重庆大学，2013.

[14] 赵林峰.全工况电动助力转向系统建模控制及试验研究[D].合肥:合肥工业大学，2009.

[15] 王先耀.基于滑模控制的线控转向系统稳定性研究[D].淄博:山东理工大学，2012.

[16] 高明，赵楠，张荣芸.基于LabVIEW的ESP硬件在环仿真实验台开发及仿真研究[J].汽车零部件，2013(6):53－56.