摇臂推杆式电磁主动悬架的鲁棒控制与优化∗

谷 成，殷 珺，陈辛波

（1.同济大学汽车学院，上海 201804； 2.同济大学新能源汽车工程中心，上海 201804）

前言

主动悬架在提高车辆行驶舒适性和操纵稳定性等方面效果显著，尤其是电磁式主动悬架具有响应快、可馈能等优点，成为国内外研究热点[1]。文献[2]中采用直线电机作为主动悬架作动器，具有安装方便等优点。文献[3]中提出了一款柱状永磁作动器，并考虑系统不确定性进行鲁棒控制，与被动悬架相比，在悬架动行程不变的情况下舒适性提高40%，但由于直线电机功率密度不高而普遍存在质量体积较大的缺点。为采用旋转电机，须引入机构将其旋转运动转化为悬架的往复直线运动。文献[4]中开发了一款滚珠丝杠式电磁作动器，并结合μ综合理论设计了鲁棒控制器。文献[5]中则采用齿轮齿条式作动器，通过匹配电机与传动系参数的方式来提高系统效率。文献[6]中提出一种新型“两腿”式传动机构，经试验验证，其机械效率比滚珠丝杠和齿轮齿条机构高，但有效行程较短。

悬架系统中导向机构使弹簧等机械元件在运动过程中呈现出非线性特性[7]，在传统确定参数模型中悬架刚度等参数存在简化误差，文献[8]中基于确定模型采用最优控制策略，在实际应用中不能保证系统实现最优性能。滑模变结构控制不依赖于所建模型，但在定义滑模面时往往需要目标控制力、状态变量和路面扰动等信息[9]，基于滑模观测器的状态估计和扰动估计准确性在实际应用中仍有待验证。文献[10]中运用鲁棒控制在给定频段内更好地抑制了车体振动，在固有频率下车体垂直振动加速度增益降低了9dB。针对人体敏感频率范围，文献[11]中对主动座椅悬架系统设计了H∞控制器，并采用KYP理论对输出量的无穷范数进行优化。文献[12]中采用动态输出反馈对半车模型进行鲁棒控制，提高了行驶平顺性和操纵稳定性。文献[13]中设计了鲁棒H2/H∞控制律，通过实例仿真验证了控制的有效性和可行性，改善了乘坐舒适性。但当不确定性因素较多时，为保证在所有摄动区间内均满足稳定性要求，基于传统鲁棒H∞控制系统存在保守性较高的缺点。

本文中针对一种新型摇臂推杆式电磁主动悬架，结合该悬架系统非线性和不确定性引起的参数摄动，设计鲁棒H∞控制器。通过算例验证该主动悬架系统对参数摄动的鲁棒性，改善行驶舒适性和操纵稳定性，并提出一种优化策略以降低控制器的保守性。

1 摇臂推杆式电磁主动悬架

图1为一种摇臂推杆式电磁主动悬架，其中电机、减速器、摇臂和推杆构成电磁作动器。电机与减速器一体化集成设计，固连于车身，减速器输出轴与摇臂固连，推杆下端以转动副与下横臂连接，上端以转动副与摇臂连接，弹簧等零件安装位置不变。假设车身固定，当车轮受路面激励向上跳动时，推杆随下横臂向上运动，使摇臂绕减速器输出轴转动，并压缩弹簧。电机输出转矩经减速器控制摇臂和推杆来实现主动减振。当电机输出转矩与转速方向相反时，电机处于发电状态，可回馈振动能量。该摇臂推杆式电磁作动器结构新颖，规避了传统滚珠丝杠或齿轮齿条式作动器的专利保护，加工容易；悬架作动器模块化设计，替换性强，适用于不同悬架类型和参数。

图1 摇臂推杆式电磁主动悬架

2 系统建模

2.1 参数摄动范围

一方面，由于悬架系统中导向机构的存在和弹簧的非竖直布置，使弹簧力与作用于车轮的垂向力存在偏差；另一方面，由于电机转子等转动惯量转换到减速器输出轴的转动惯量具有放大效应，并通过摇臂推杆机构作用于车轮，导致车辆等效簧下质量增加。在ADAMS环境中建立模型进行运动学与动力学分析，得到系统等效弹簧刚度和等效簧下质量随车轮垂向位移变化的非线性关系，如图2所示。

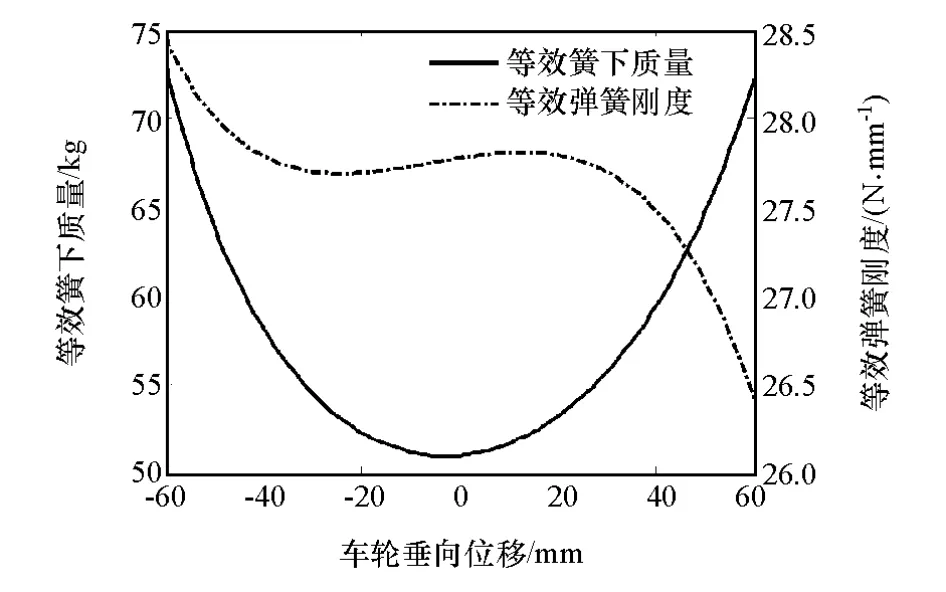
图2 等效弹簧刚度和等效簧下质量与车轮垂向位移的非线性关系

由图2可知，考虑导向机构与摇臂推杆等影响，悬架等效刚度变化范围约±4%。在车轮跳动范围内，簧下质量增量变化范围为50～75kg，设车轮质量为40kg，则等效簧下质量标称值为102.5kg，摄动范围为±13%。

此外，乘客人数与轮胎压力的不确定性引起车身质量和轮胎刚度等参数摄动，设簧上质量与轮胎刚度摄动范围均为±10%。从而，1/4车辆悬架系统参数如表1所示。

表1 系统参数摄动范围

需要说明的是，相比于传统车辆，本文中提出的摇臂推杆式电磁主动悬架的簧下质量增加了一倍，这是电机转子转动惯量经过减速器后在输出端具有放大效应导致的，是采用旋转式作动器与减速器结构的固有属性，通过匹配较小功率的电机和减速比可降低等效簧下质量，这也是本方案后续需要改进之处；另一方面，尽管等效簧下质量增加，使车辆垂向性能有恶化趋势，但采取合适算法实现主动控制，对悬架性能进行频率整型，可实现更优的行驶舒适性和操纵稳定性，这也是开发主动悬架的主要目的。

2.2 不确定性建模

建立如图3所示的1/4车辆悬架模型，设簧下质量为m1，簧上质量为 m2，轮胎刚度为k1，忽略轮胎阻尼，悬架刚度为k2，路面扰动位移为q，簧下质量位移为z1，簧上质量位移为z2，主动力为u。

根据牛顿第二定律，建立悬架系统2阶常微分方程:

图3 1/4车辆主动悬架模型

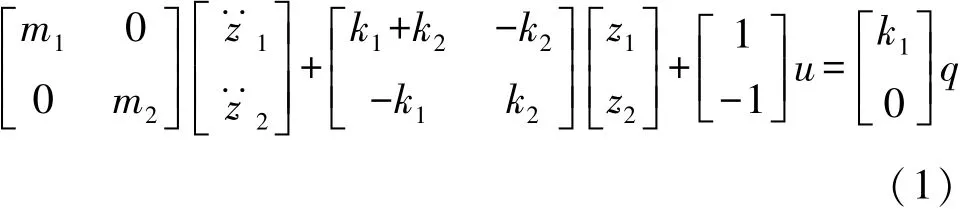
即

在式(2)中，含参数摄动的质量矩阵M为

将质量矩阵的逆矩阵M－1表示为含摄动矩阵的上线性分式变换:

同理，含参数摄动的刚度矩阵K为

将刚度矩阵表示为含摄动矩阵的上线性分式变换形式:

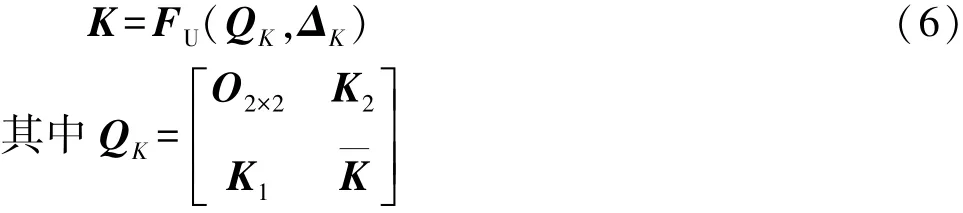
从而，基于式(2)，含参数不确定性的系统模型如图4所示。

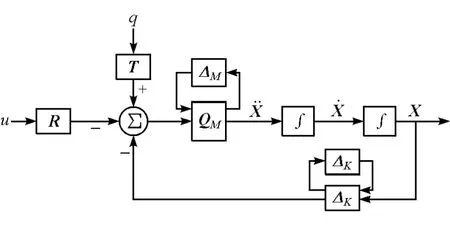
图4 考虑参数不确定性的系统结构图

3 鲁棒H∞控制

1/4车辆悬架闭环系统结构如图5所示，设G为含参数摄动系统，q为路面扰动输入，Z为期望输出与测量输出，Kc为控制器，n为测量噪声，u为被控输入。

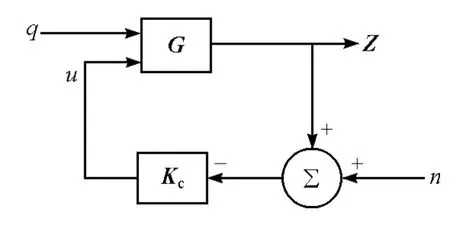
图5 闭环系统结构

可以证明，以簧上质量、等效簧下质量、等效弹簧刚度和轮胎刚度构成的标称系统可控且可观测，为最小实现系统，且闭环系统特征值开左半复平面，系统渐近稳定，从而标称系统内部稳定等价于有界输入有界输出稳定。闭环系统鲁棒稳定，当且仅当在参数摄动范围内所有闭环摄动系统G均内部稳定。

结合图5，含参数摄动的系统鲁棒性能应包括以下3个方面，并分别得到对应的传递函数。

(1)反映期望输出Z对扰动输入q抵抗能力

式中I为单位矩阵。

(2)反映抵抗测量误差n的能力

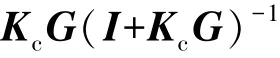
(3)要求控制力小

综上可得，摄动系统鲁棒H∞控制优化目标为:在参数摄动范围内系统鲁棒性能稳定，且上述鲁棒性能指标传递函数的无穷范数最小。为表征系统对单位摄动的鲁棒性能，引入相应的权重函数，求系统满足上述最佳性能时传递函数的无穷范数最小值:

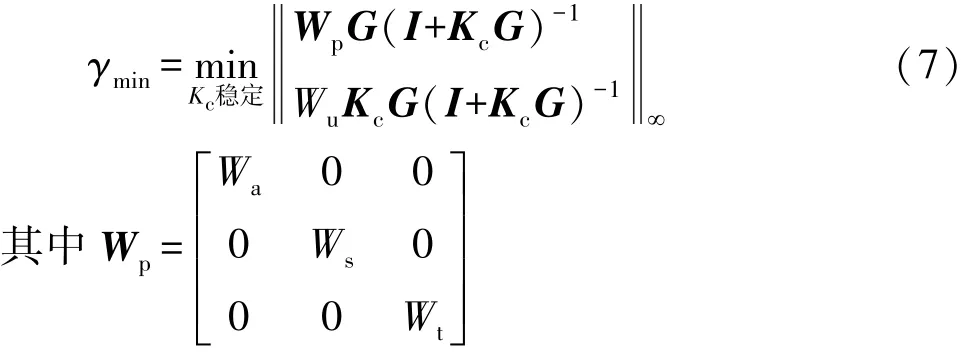
式中Wa，Ws，Wt和Wu分别为车身加速度、悬架动行程、轮胎动位移和主动力的权重函数。

从而，在路面扰动输入q的影响下，将上述加权车身加速度、悬架动行程、轮胎动位移和主动力作为期望输出优化目标，并将含测量噪声n的悬架动行程信号作为控制器输入，计算主动控制力u，构成输出反馈闭环控制，如图6所示。

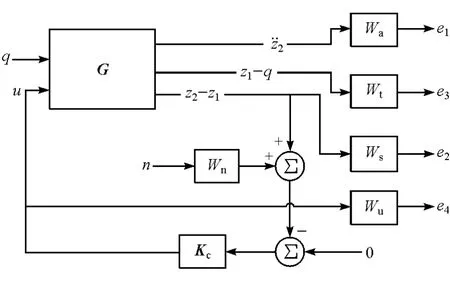
图6 闭环系统控制器设计

基于被动悬架各输出性能指标的频率响应特性，经拉普拉斯变换，选择合适滤波器，确定主动悬架期望输出的各悬架性能指标频率响应特性，并微调权重函数，经反复试验，从而分别确定相应的车身加速度权重(s为拉普拉斯算子)，悬架动行程权重，轮胎动位移权重Wt＝0.1，主动力权重 Wu＝0.002，测量噪声权重与主动力权重类似，在全频率范围内设为常数，Wn＝0.001。

经迭代计算得闭环系统鲁棒稳定性μ值为0.221，小于1，表明在参数摄动范围内，系统满足鲁棒稳定，且有一定裕度，此时，式(7)的最优解γmin＝2.5469。

4 仿真分析与试验验证

4.1 频域响应

对表1中4个参数，分别取样本值为摄动上界值、标称值和摄动下界值，排列组合产生81种摄动系统。开环系统与闭环系统下车身加速度对路面扰动的幅频特性如图7所示，虚线代表标称系统幅频特性，实线代表81组摄动系统幅频特性。

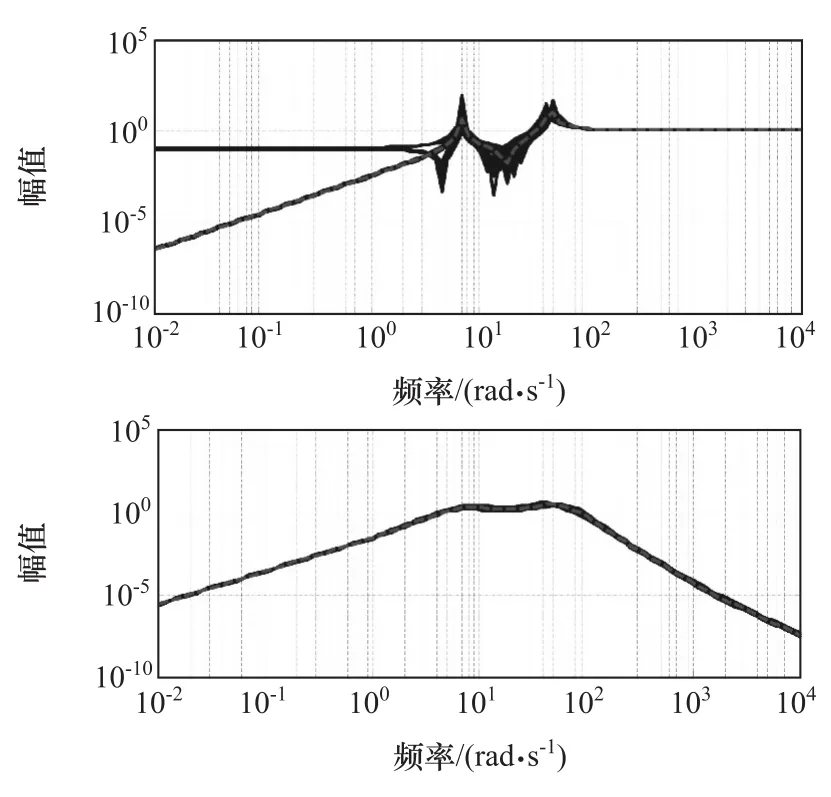
图7 车身加速度幅频特性比较

从图7可得，在全频率范围内，闭环系统幅频特性曲线更加集中，表明参数摄动对车身加速度影响明显减小，系统对参数摄动具有良好的鲁棒性，且闭环系统曲线更加平滑，系统有更好的阻尼特性。在人体舒适性敏感的4～8Hz频率范围内，主动控制时闭环反馈系统的车身加速度幅值降低，表明行驶舒适性得到提高。

4.2 时域响应

针对实际工况中，摄动参数连续变化的情况，为验证该电磁主动悬架的可行性和鲁棒控制算法的有效性，试制该摇臂推杆式电磁主动悬架系统样机，并搭建1/4车辆悬架试验台架，如图8所示。

图8 摇臂推杆式电磁主动悬架样机

在图8中，主动悬架样机通过轮胎悬置于转鼓上，采用铁板模拟车身质量，它可沿导轨垂向移动。测功电机经过同步带减速器驱动转鼓，转鼓周围布置凸块，以模拟路面扰动激励。

根据测得的弹簧变形量Δx，设计鲁棒控制器KC以产生主动力u。进而，根据减速器输出转矩T′与主动力u之间的关系，结合减速比i，实时得到电机输出转矩的目标信号T，输入电机控制器，实现该摇臂推杆式电磁主动悬架系统的输出反馈闭环控制，改善期望输出的鲁棒性能。其中，电机控制器与旋转式永磁同步电机作为集成模块被引入使用，其输出转矩控制算法成熟，精度高，可实现性强。作动器输出转矩的闭环控制系统结构如图9所示。

图9 控制系统结构

为得到图中减速器输出转矩T′与主动力u之间的关系，根据ADAMS运动学与动力学模型，首先，由弹簧变形量Δx标定得到车轮垂向位移s，其次，建立减速器输出转矩与主动力比值随车轮垂向位移s的变化关系，如图10所示。

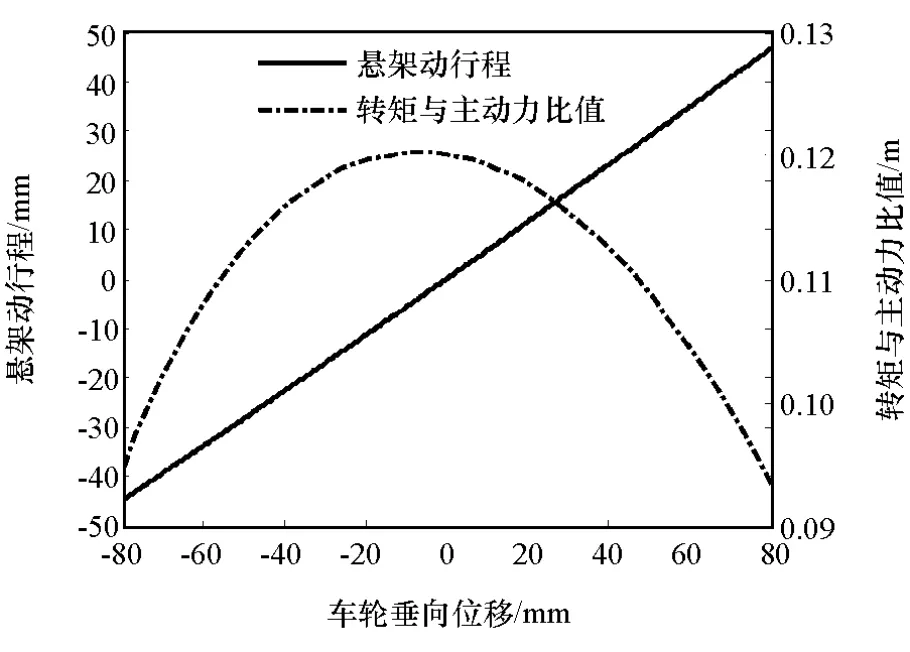
图10 悬架行程与减速器输出转矩和主动力比值随车轮垂向位移变化关系

为验证电磁主动悬架的可行性和鲁棒控制算法的有效性，分别考察有无主动控制时，该悬架在凸块激励下的时域响应。考虑到橡胶衬套和摩擦等因素，实际悬架系统中含有阻尼，在无主动控制情况下视为被动悬架。由于轮胎动位移信号不易得到，本文中采用车轮加速度信号代替。经滤波等数据处理，分别得到两种模式下车身加速度、弹簧变形量和车轮加速度时域响应对比，如图11所示。

由图11可得，在路面扰动激励下，以及悬架刚度和等效簧下质量等参数连续变化的情况下，相比被动悬架，鲁棒控制主动悬架能更快稳定，且车身加速度和弹簧变形量更小，车轮加速度时域响应近似相等，证明了本文中提出的摇臂推杆式电磁主动悬架方案是可行的，鲁棒控制算法对参数摄动等不确定性因素具有良好的鲁棒性。

5 鲁棒控制器的优化

上述针对参数不确定性所设计的H∞控制器实现了闭环摄动系统的鲁棒稳定性，且鲁棒性能满足控制要求，但因须同时满足簧上质量、等效簧下质量、等效弹簧刚度和轮胎刚度等4组较大范围的参数摄动，控制器保守性较大。

将车身质量参数作为变量，其它参数均取标称值，考察簧上质量参数摄动对系统鲁棒性能的影响。设车辆以20m/s速度行驶在C级路面，在60s时间范围内，分别计算不同簧上质量所对应的闭环悬架系统鲁棒性能指标与主动控制力的均方根值，如图12所示。

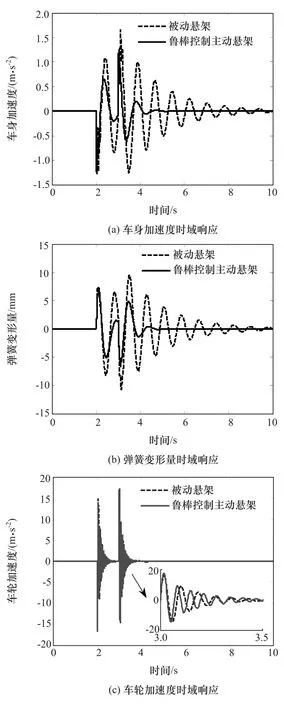
图11 参数摄动下时域响应

从图12可得，在簧上质量参数变化范围内，车身加速度和轮胎动位移的均方根值均保持一致，鲁棒H∞控制通过调节输出主动力确保所有摄动系统的车辆行驶舒适性和操纵稳定性与标称系统基本保持一致，体现了鲁棒控制对参数摄动具有良好的鲁棒性。但对于簧上质量参数摄动较大的闭环系统来说，一方面，为了保证其期望输出鲁棒性能，须输出较大的主动力；另一方面，使其输出的悬架性能与标称系统鲁棒性能保持一致，本身也存在着保守性较高的缺点。

图12 不同簧上质量对应的鲁棒性能与主动力均方根值

可以通过调节权重函数来提高系统行驶平顺性或操纵稳定性，但二者通常无法同时优化。本节中提出一种鲁棒控制器优化算法，以降低控制器保守性，提高系统综合鲁棒性能。由于车身质量参数在车辆行驶过程中基本保持不变，且可由直线位移传感器静态获得，因此，可将其分段处理，以减小簧上质量参数摄动范围。对应于不同区间的闭环摄动子系统，微调车身加速度、悬架动行程、轮胎动位移和主动力等权重函数，使其输出悬架性能最优，分别设计对应的鲁棒控制器。根据系统原有的传感器获得簧上质量参数，通过静态查表的方式选择合适的控制器，实现自适应鲁棒H∞控制，且不增加系统成本。

下面结合具体算例对上述优化策略进行验证。对于1/4车辆悬架系统，标称车身质量为500kg，摄动范围为450～550kg，将车身质量摄动范围等分为5段，每段摄动范围为±10kg，分别建立对应区间的鲁棒控制器。以簧上质量为450kg、其它参数均为标称值的闭环主动悬架系统为例，原控制器和自适应控制器参数如表2所示。

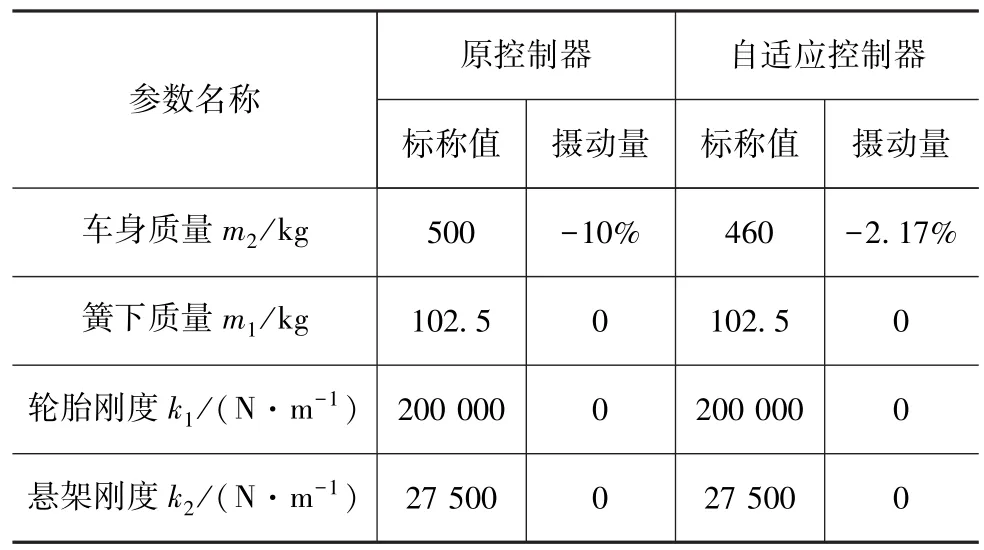
表2 系统参数比较

根据20m/s的车速和C级路面条件得到路面权重函数，输入扰动为均值为0、方差为1的白噪声。考察60s时间范围内不同控制器的各悬架性能和主动力均方根值，如表3所示。

表3 不同控制器各性能及主动力均方根值比较

由表可知，相比原控制器，自适应控制下的车身加速度均方根值降低了1.53%，悬架动行程降低了7.59%，轮胎动位移降低了23.53%，主动力降低了15.12%。在保证系统稳定性和降低输出主动力的情况下，全面改善了悬架系统的综合鲁棒性能，降低了原控制器由于摄动范围较大而存在的保守性。

此外，车辆行驶过程中车身质量基本保持不变，无需切换控制器，避免了控制器频繁切换过程可能给乘客带来的抖动与冲击感。根据标定的车身质量，通过静态查表方式自适应选择合适的控制器，保证了系统控制实时性，且不增加系统传感器的成本，可实现性强。

6 结论

(1)针对一种新型摇臂推杆式电磁主动悬架设计鲁棒控制器，该电磁作动器具有结构新颖、加工容易和模块化设计等优点。根据悬架等效刚度和等效簧下质量等参数摄动范围，对该主动悬架系统进行鲁棒H∞控制。频域和时域响应结果表明，与被动悬架相比，闭环主动控制显著提高了行驶平顺性和操纵稳定性，且对扰动具有良好的鲁棒性。

(2)为降低控制器的保守性，将车身质量参数摄动范围减小，改进设计自适应鲁棒H∞控制器，采用静态查表离线控制方式保证实时性，且行驶过程中无需切换控制器，避免了可能对乘员的冲击感。

[1] 喻凡，张勇超.馈能型车辆主动悬架技术[J].农业机械学报，2010，41(1):1－6.

[2] JONES W.Easy ride:Bose Corp.uses speaker technology to give cars adaptive suspension[J].IEEE Spectrum，2005，42(5):12－14.

[3] VAN D，GYSEN B，BESSLINK I，et al.Robust control of an electromagnetic active suspension system:simulations and measurements[J].Mechatronics，2013，23(2):204－212.

[4] HUANG K，YU F，ZHANG Y.Active controller design for an electromagnetic energy-regenerative suspension[J].International Journal of Automotive Technology，2011，12(6):877－885.

[5] LI Z，ZUO L，LUHRS G，et al.Electromagnetic energy-harvesting shock absorbers:design， modeling， and road tests[J].Vehicular Technology， IEEE Transactions on，2013，62(3):1065－1074.

[6] MARAVANDI A，MOALLEM M.Regenerative shock absorber using a two-leg motion conversion mechanism[J].Mechatronics，IEEE/ASME Transactions on，2015，20(6):2853－2861.

[7] 宁国宝，王永湛，余卓平，等.悬架系统非线性特性对车辆垂向性能的影响[J].同济大学学报(自然科学版)，2009，37(8):1065－1069.

[8] 罗鑫源，杨世文.基于AHP的车辆主动悬架LQG控制器设计[J].振动与冲击，2013，32(2):102－106.

[9] PAN H，SUN W，GAO H.Finite time tracking control of vehicle suspension systems[C].Control Conference(CCC)，2015 34th Chinese， IEEE，2015:8046－8050.

[10] 陈彦秋，宋鹏云，张继业，等.车辆能量回馈式主动悬架μ综合控制[J].西南交通大学学报，2012，47(6):974－981.

[11] SUN W，LI J，ZHAO Y，et al.Vibration control for active seat suspension systems via dynamic output feedback with limited frequency characteristic[J].Mechatronics，2011，21(1):250－260.

[12] 李荣，焦晓红，杨超.基于动态输出反馈的半车主动悬架系统鲁棒控制[J].振动与冲击，2014，33(7):187－193.

[13] 龙垚坤，文桂林，陈哲吾.汽车主动悬架鲁棒保性能控制仿真研究[J].汽车工程，2014，36(2):216－221.