2017年理综全国Ⅰ卷第21题评析与教学启示

许冬保

(江西省九江市第一中学,江西 九江 332000)

1 原题再现

2017年全国理综卷Ⅰ卷第21题原题如下.

图1

(A)MN上的张力逐渐增大.

(B)MN上的张力先增大后减小.

(C)OM上的张力逐渐增大.

(D)OM上的张力先增大后减小.

2 解答策略

在共点力平衡问题中,有一类通过控制某一物理量,使物体的状态发生缓慢变化的动态平衡问题.该类问题涉及动态分析方法,要求在事物的动态变化中洞察、分析、推理,进而解决问题,这类问题的常规处理策略是解析法和图解法.以下从不同的视角对试题予以分析.

2.1 解析法

解析法是对研究对象的某一状态进行受力情况的分析,依据平衡条件,建立方程,求出因变量与

自变量之间的函数关系,然后根据自变量的变化规律确定因变量的变化情况.若物体仅受3个力作用,可寻找与力三角形相似的几何三角形,建立比例关系,将力的大小变化问题转化为几何三角形边长的变化问题进行讨论.[1]

解法1:正交分解法.

图2

如图2所示,在某一位置对重物进行受力分析,重物受到重力mg、绳OM的张力F1及绳MN的张力F2作用.建立平面直角坐标系,设绳OM与竖直方向的夹角为θ,F2与x正方向的夹角为β.由平衡条件,有

F2sinβ+F1cosθ-mg=0,F2cosβ-F1sinθ=0，

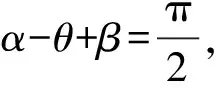
综上,在整个变化过程中,力F1先增大后减小;力F2逐渐增大.选项(A)、(D)正确.

解法2:相似三角形法.

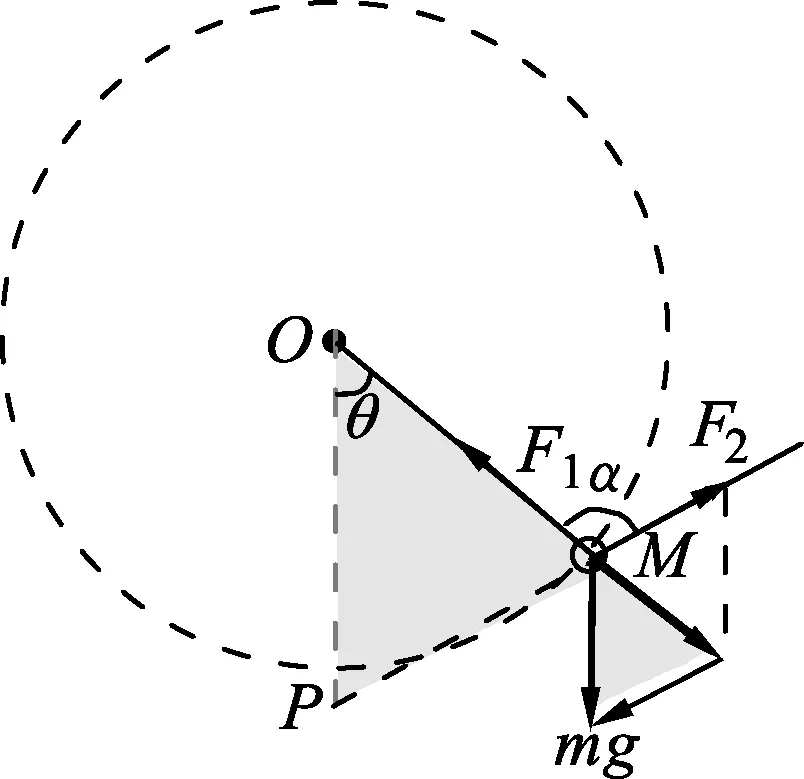
图3

某一位置,绳OM与竖直方向的夹角为θ,受力情况如图3所示,将力F2反向延长与过O点的竖直线相交于P点,由平衡条件知,重力mg与力F2合成所得合力与F1等值反向.考察图3,图中两填充三角形相似,对应边成比例.因此

于是可解得F1、F2.所得结果同上.

2.2 图解法.

图解法是根据平行四边形定则或三角形定则画出不同状态下的力的矢量图,然后由力矢量的变化判断各力的变化情况.图解法借助于矢量分析,能直观地得到物理量之间的关系以及变化趋势,从而极大地简化分析及运算过程,提高思维的品质.[2]

解法3:图解法

图4

如图4所示,设绳OM、MN的张力分别为F1、F2.在OM由竖直被拉到水平的过程中,重物缓慢拉起,重力mg及力F1、F2构成封闭矢量三角形.由于夹角α保持不变,因此,由几何知识可知,矢量F1之箭尾或矢量F2之箭头在以重力矢量大小为弦的同一圆周上滑动.以动态的视角考察图4,可直观得到,力F1先增大后减小(最大值对应圆的直径);力F2逐渐增大(其最大值亦对应圆的直径,但F2以此收尾).所得结果同上.

3 另类分析策略

一般物体的平衡,除了满足共点力作用下的平衡条件之外,还有一个条件是满足力矩平衡条件.后者在全国高考(上海市除外)考试大纲中未作要求.力矩平衡条件,即物体所受外力对某一转轴的合力矩为零.力矩平衡条件作为拓展性内容,对参与物理竞赛及自主招生考试的考生,是必须掌握的学习内容.

3.1 定性分析

解法4:力矩平衡条件定性分析法.

若以O点为转动轴,在重物缓慢移动过程中,合力矩为零.显然重力的力矩(顺时针)不断增大,而F2之力矩(逆时针)也不断增大,由于其力臂保持不变,故力F2逐渐增大.若选择图1中绳端点N为转动轴,等效于绳OM逆时针转动,显然重力之力矩先增大后减小,而力F1之力臂保持不变.因此,力F1大小先增大后减小.所得结果同上.

3.2 定量分析

解法5:力矩平衡条件定量分析法.

重物在某一位置时,同样设绳OM与竖直方向的夹角为θ,参考图3,由力矩平衡条件,有

mg·OM·sinθ=F2·OM·sinα.

若以绳端点N为转动轴,等效于绳OM逆时针转动.同理,有

mg·MN·sin(π-α+θ)=F1·MN·sinα，

4 立意分析

物体的平衡是力学体系的基础和核心知识,相互作用观念下的动态平衡及其应用中的模型构建与分析推理,体现了高考突出对物理观念、科学思维等核心素养的考查.

共点力的平衡在考纲中属于Ⅱ类要求(与课标中的“理解”和“应用”相当).关于共点力平衡的考查,近年来高考试题主要的考查方式可划分为3类:第1类是考查受力分析、力的合成与分解的方法,根据平衡条件定性分析(如2016年桌面上的物块通过细绳跨过定滑轮及另一悬吊物块约束下的平衡问题)或通过平衡条件建立方程求解问题(如2012年拖把平衡问题);第2类是对动态平衡问题的考查,在以往的考查中,受3力作用下的平衡系统,其中,一个力的大小与方向不变,还有另一个力的方向不变,这是最经典的动平衡问题(如2012年考查木板与墙面间夹一小球,木板转动中小球的动态平衡问题);第3类是突出基础性与综合性的考查,表现为应用共点力的平衡条件解决弹簧系统的平衡问题(如2015年悬挂在弹簧下的通电导体棒在磁场中的平衡问题)、电磁感应现象中通电导体棒的平衡问题(如2016年斜面上的双棒问题)等.

2017年考查的是一个力的大小及方向不变,另两个分力方向均变化的动态平衡问题,试题构思巧妙,突破常规,要求考生灵活运用所学知识分析解决动态平衡的问题.当考生发现所给问题不符合既定动态平衡的模型时,需要考生具备提出创造性见解的能力和品质.因此,试题考查了考生的理解能力与推理能力.在物理观念及科学思维方面,有效地考查了相关的最高水平层级.

5 教学启示

物理核心素养的考查要求考生能够在不同情境下综合利用所学知识和技能处理复杂任务,具有扎实的物理观念和宽阔的物理视野,并体现出自身的实践能力、创新精神等内化的综合学科素养.核心素养下的关键能力的考查重点是,考查考生所学知识的运用能力,强调独立思考、分析问题和解决问题.2017年动态平衡问题的考查带给教学的启示主要有以下3个方面.

(1) 授人以鱼,不如授人以渔.如上所述,求解平衡问题的方法通常有,解析法及图解法.解析法中又有正交分解法、合成与分解法及相似三角法等.对于动态平衡问题的处理,一般划分为两类,即图解法及相似三角形法,而且这两种方法适用于不同的情境.在教学中,方法的应用及掌握,单凭考生通过自己的训练去掌握有关方法,效率较低.需要教师的隐性渗透与显化教学,才能领悟、促进方法的掌握,进而内化为自觉的学习行为.

(2) 跳出题海,重视科学思维.题海战术,事倍功半.教学中应重视科学思维的训练.科学思维作为对客观事物本质属性、内在规律和相互关系的认识方式,具有高度的抽象性和概括性,在教学中,要能够帮助考生正确运用科学思维方法,能从定性(或半定量)和定量2个方面进行科学推理,找出规律并形成结论[3].

(3) 讲究策略,提高思维品质.认知心理学家根据解决问题的效率将解题策略分为强方法和弱方法.对解决问题来说,效率较高的方法,属强方法.效率较低的方法,则属弱方法.物体只受3个共点力作用而处于动平衡状态,如果一个力矢量不变,另外还有一个力的方向不变,图解法是强方法,解析法是弱方法;如果一个力矢量不变,另两个力均在变,相似三角形法是强方法,矢量图解法是弱方法.以上对试题的不同解法涉及不同的思维方法,不同的思维方法能反映思维品质的优劣.

总之,物理核心素养作为物理教学的重要目标,应当将物理观念、科学思维、科学探究及科学态度与责任等核心素养的培养真正落实于教学活动中.

1 杨榕楠.更高更妙的物理·高考高分与自主招生决胜篇[M].杭州:浙江大学出版社,2013.

2 江四喜.物理竞赛解题方法漫谈[M].合肥:中国科学技术大学出版社,2014.

3 教育部基础教育课程教材专家工作委员会,普通高中课程标准修订组.普通高中物理课程标准 (征求意见稿)[R].北京,2016.