一道求微分方程特解习题的推广
高 芳,熊艳琴
(1.池州学院数学与计算机学院,安徽池州247100;2.南京信息工程大学数学与统计学院,江苏南京210044)
二阶常系数线性非齐次微分方程y″+py′+qy=f(x)的求解是高等数学教学中的一个重要内容,一般的高等数学教材[1-2]均会讨论当f(x)=Pm(x)eλx时(其中Pm(x)是m次多项式)特解的形式。
当非齐次项f(x)=Pm(x)eλx时,利用待定系数法,可得特解的一般形式为y*=xkQm(x)eλx
其中k=0,1,2,分别对应当λ不是特征根、单特征根和二重特征根的情形。
一般地,在利用待定系数法求特解时,计算比较繁琐,计算量较大,教学中发现学生经常会出现计算错误。文献[3-5]讨论了二阶常系数非齐次线性常微分方程的一些简便求解方法。本文由一道例题求解出发,给出了当Pm(x)为二次多项式时一个容易计算和记忆的特解公式。
1 待定系数法
先从非齐次项中Pm(x)是最简单的二次多项式进行分析。
例:求微分方程y″-6y′+9y=x2e3x的一个特解。
解:由于f(x)=x2e3x,而λ=3是对应的齐次微分方程特征方程的二重根,因此可设特解为
y*=x2(l x2+m x+n)e3x,对y*求导得

将y*′,y*′′代入原方程,得

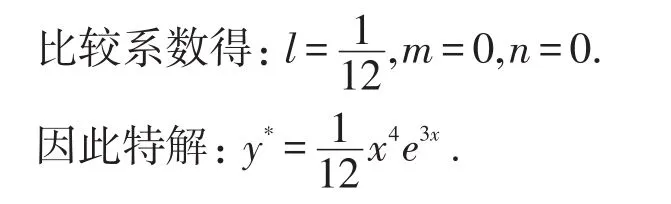
在此例中,通过求解可知m,n均为0,特解形式变得相对简单,特解的系数只与f(x)=x2e3x的二次项系数有关。对于f(x)=(ax2+bx+c)eλx的一般情形,二阶常系数线性非齐次微分方程的特解形式又该如何?下面我们进行具体分析。
2 主要结论
对于微分方程
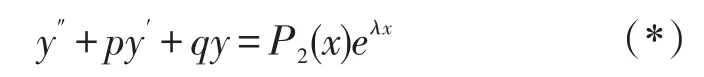
当P2(x)=ax2+bx+c(a≠0)时,分三种情形进行讨论。
情形一、当λ不是特征方程的根时,即λ2+pλ+q≠0时,可设特解为

对y*求导得:

通过比较系数,得:
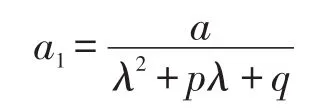
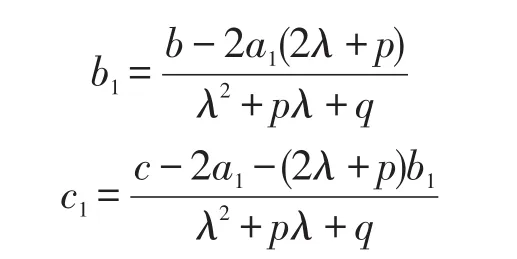
此时,由计算结果可知特解表达式中的未知系数由a,b,c和p,q,λ的值唯一确定.
情形二、当λ是特征方程的单根时,即λ2+pλ+q=0,2λ+p≠0时,可设特解为
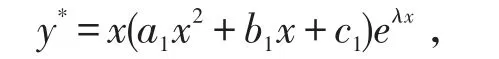
对y*求导得:
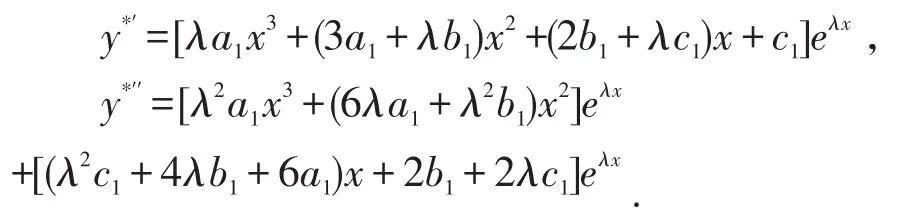
将y*′′,y*′,y*代入方程(*)中,整理化简得:

通过比较系数,可得:

特别地,当Pm(x)=ax2时,
此时特解由a,p,λ的值唯一确定,且特解形式相对简单.
情形三、当λ是特征方程的二重根时,即当λ2+pλ+q=0,且2λ+p=0时,可设特解为
y*=x2(a1x2+b1x+c1)eλx,对y*求导得:
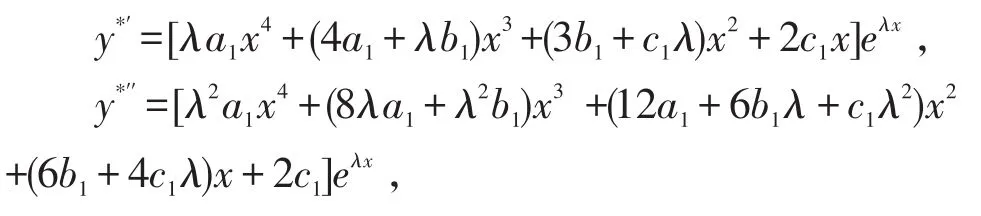
将y*′′,y*′,y*代入(*)中,化简整理得:
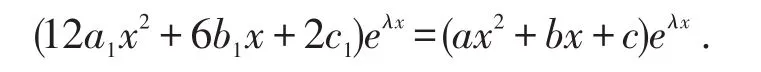
通过比较系数,可知

在情形三中,特解待定系数里的a1,b1,c1可分别由a,b,c唯一确定,且形式简单便于记忆。更一般地若f(x)=ax2eλx,在计算题中,可直接设特解为y*=a1x4eλx,求导代入方程,可简化计算,通过分析过程可知,当λ是特征方程的二重根时,特解可由较简单的形式给出。情形三下的结果可推广至f(x)=(ax3+bx2+cx+d)eλx的情形,利用待定系数法,此时特解为:y*=x2(a1x3+b1x2+c1x+d1)eλx,其中.若f(x)=ax3eλx,在计算题中,可直接设特解为y*=a1x5eλx,求导代入方程,可简化计算,并提高计算的速度和准确性。

