基于SPML和海绵边界的伪谱法弹性波模拟复合吸收边界条件

马 锐,邹志辉,2,芮拥军,贾东顺

(1.中国海洋大学海洋地球科学学院海底科学与探测技术教育部重点实验室,山东青岛266100;2.青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛266061;3.中国石油化工股份有限公司胜利油田分公司物探研究院,山东东营257022;4.中国石油集团东方地球物理勘探有限责任公司辽河物探分公司,辽宁盘锦124010)

地震波正演数值模拟的计算区域大小有限,若对计算区域的边界不做任何处理,地震波到达计算区域边界时会产生数值噪声,对正常传播的地震波造成干扰。为逼近无限大空间的地震波传播,需要在有限区域的边界设计数值边界条件,以吸收边界产生的数值噪声。

早期地震波正演模拟多采用基于旁轴近似的单程波方程吸收条件[1-2],该吸收条件仅对接近垂直入射至边界的地震波具有较好的衰减,对大入射角地震波的衰减效果较差。另一种被广泛应用的吸收边界条件是海绵吸收边界条件,该边界条件在正常运算区域外部加了一个衰减层,使得入射至边界衰减层的地震波振幅被逐渐衰减而不产生明显反射[3]。海绵吸收边界的吸收效果取决于衰减系数和边界宽度等参数,为了达到较好的衰减效果人们通常要将衰减边界设置得足够宽,以满足对地震波振幅衰减程度的要求,这会大幅增加计算量和对计算机内存的占用[4]。

完全匹配层吸收边界条件(PML)最早由BERENGER[5]在研究电磁场有限域波动问题时提出,相比传统的吸收边界条件,PML的吸收效果更好[6-7]。随后该吸收边界被推广到声波和弹性波的数值模拟[8-13]。常规PML吸收边界按照不同的实现方式,可以分为分裂格式PML(SPML)和非分裂格式PML(NPML)[14]。NPML不需要分裂波场分量,编程实现较容易,但实现过程中包含大量卷积,计算过程复杂[15-16]。为了提高NPML计算效率和简化运算过程,前人提出了非卷积形式的NPML吸收边界[17]。SPML通过分裂波场的传播分量来实现,计算方程简洁,计算量相对NPML更小,所以目前很多正演模拟仍然采用SPML[18-19]。

然而,SPML边界条件对于切向入射到边界的地震波吸收效果差,当入射波频率较低时还会在边界附近产生虚假反射[20]。针对上述问题,前人提出一种不分裂褶积型PML边界条件(CPML)[21-22],其在声波和弹性波数值模拟中均取得了较好的应用效果[23-24]。但是,CPML在推导中使用了递归卷积的方法,导致其应用受到较多限制,如无法适应空间网格的灵活变化,难以用于高阶的时间离散格式等[25]。与CPML相比,SPML限制条件少,可以适用于各种正演模拟方法。可见,改进SPML以提高边界的吸收效果对于地震波数值模拟在地震学不同领域的应用具有重要意义。

针对SPML对切向入射到边界的地震波吸收效果差的问题,本文将SPML边界与海绵吸收边界进行空间衔接,构建内部为SPML,外部为海绵吸收边界的复合吸收边界,使SPML未吸收完全的地震波得到二次衰减。同时针对常规海绵边界对大角度入射波吸收不足的问题,改进了其衰减函数,以进一步改善复合吸收边界的吸收效果。

1 SPML边界吸收能力的理论分析

伪谱法弹性波正演模拟使用有限差分求时间导数,通过傅里叶变换在波数域求空间导数,具有节省空间离散样点数和不产生空间数值频散的优点[26-28]。

COLLINO等[29]通过复坐标伸展变换推导出了各向同性介质一阶应力-速度方程的完全匹配层吸收边界条件,其应用在伪谱法数值模拟中需转化到时间-波数域,具体形式如下:

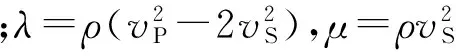
(3)

d(x)和d(y)是笛卡尔坐标系沿x和y方向的衰减函数,其表达式为[31-32]:

式中:δ为SPML边界的总厚度;R为理论反射系数。

在SPML区域内,衰减函数d(x)和d(y)控制了对边界入射波的吸收能力,它们通过复坐标伸展变换被引入到弹性波方程。二维空间的复坐标伸展变换公式为[33-34]:

(6)

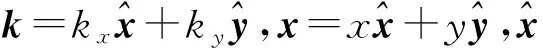
平面波在SPML区域沿x方向的衰减形式为[35]:

(7)

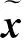
(8)

衰减项Dx在正常运算区域中的值为1,表示未对地震波进行衰减,在SPML区域中的值按指数形式衰减。波矢量的x和y方向分量可以写为:

(9)

式中:γ是波前面法向与对应边界法向(例如图1中x轴方向)的夹角;cp为相速度。将(9)式代入(8)式,Dx的表达式变为:

(10)

当入射波传播方向近似平行于边界时,波前面的法线方向n与x轴的夹角γ趋于90°(如图1所示),Dx趋近于1,表明SPML边界对大角度入射波几乎没有吸收。

衰减项Dx随入射角γ的变化情况如图2所示。这里用到的地震纵波速度vP为3000m/s。当地震波入射角γ趋于90°时,边界所对应的衰减系数项Dx趋近于1,导致入射到边界的地震波所受衰减很小,因此SPML边界难以对其有效吸收。

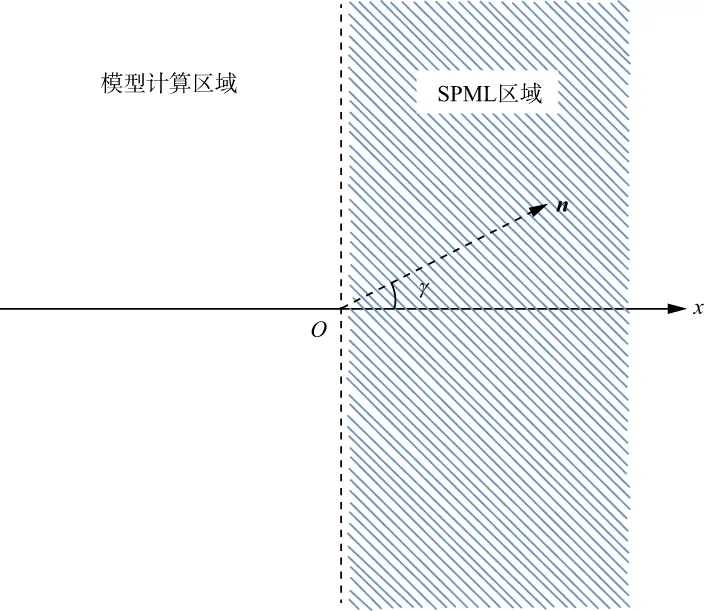
图1 模型正常计算区域与SPML区域的几何关系

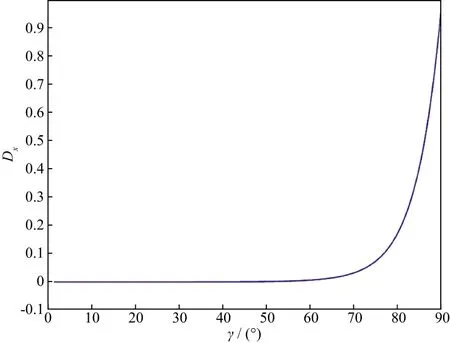
图2 SPML边界衰减项Dx与地震波入射角γ的关系

2 复合吸收边界

2.1 复合吸收边界的结构

复合吸收边界的基本思想是在SPML吸收边界之外添加一层海绵吸收边界,以对SPML边界未完全吸收的地震波进行二次衰减,对其充分吸收。复合吸收边界的结构如图3所示。

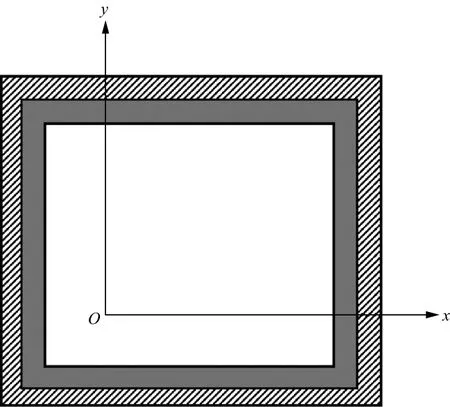
图3 复合吸收边界结构

在图3中,整个区域由内至外依次是正常运算区域(白色)、SPML边界(灰色)和海绵吸收边界(阴影)。上、下SPML边界只衰减含有y方向偏导数的波场分量,左、右SPML边界只衰减含有x方向偏导数的波场分量。当未被SPML边界充分吸收的地震波进入到海绵吸收边界区域时,海绵吸收边界会进一步对其进行衰减,实现对边界波场的二次衰减。

2.2 海绵吸收边界及其改进

由于海绵吸收边界的作用是对SPML边界未完全衰减的地震波作进一步衰减,它应该能够吸收大角度入射波。然而,常规海绵吸收边界[2]对于大角度边界入射波的吸收能力也不够强,因此有必要对常规海绵吸收边界进行改进,以提高其对大角度边界入射波的衰减效果。

常规海绵吸收边界条件在计算区域外划定边界层,在数值模拟过程中将质点的速度值和应力值在边界内分别乘以指数型衰减函数,使得地震波在边界内逐渐衰减而不产生反射,从而实现对地震波的吸收。常规海绵吸收边界的指数型衰减函数C在第i层的表达式为[2]:

(11)

式中:i代表海绵吸收边界内的边界层号;l为海绵吸收边界总层数;α为衰减系数。

当以大角度入射至边界的地震波传播方向与海绵边界切向接近平行时,其主要沿着衰减系数较小的表层传播,海绵边界的衰减效果有限,难以在复合边界中起到对SPML边界剩余波场的充分吸收。为使海绵边界在沿边界的切线方向也具备一定的衰减能力,我们将海绵吸收边界的衰减函数由仅沿y方向的一维变化推广为沿x和y方向的二维变化,使指数型衰减函数C具有沿边界法线方向和切线方向同时衰减的能力。改进后的衰减函数C′在(i,j)位置(i代表海绵吸收边界内的边界层号,j代表每层吸收边界的网格点号)的表达式为:

式中:α和β分别代表沿边界垂向和切向的衰减系数;Nx,Ny代表正演区域沿纵、横向的网格点数。由于地震波横向振幅变化剧烈,会产生明显的反射噪声,所以衰减函数沿x轴方向的变化需要足够缓慢。一种设置方法是使周期T与网格间距dx或dy的乘积大于地震波的一个波长λ。

图4显示了海绵吸收边界改进前、后的衰减函数C和C′的分布。y=0是海绵边界与SPML边界的交界。图4a和图4b分别对应(11)式和(12)式的衰减函数,参数Nx=601,dx=10,dy=10,T=100。对于l=10的边界,对应的垂向和切向衰减系数分别为α=0.04,β=0.20。

图4 常规海绵吸收边界(a)与改进型海绵吸收边界(b)的衰减函数值

图4a中常规海绵边界的衰减函数在y方向上呈指数变化,而边界内各层的衰减函数值在x方向都为常量。若地震波以大角度入射至海绵边界时(即接近平行于x轴方向),由于其表层衰减函数值趋于1(等于1表示没有衰减),致使传播至表层的地震波不能得到快速有效的吸收,因此常规海绵吸收边界所采用的衰减函数在沿x方向的衰减能力不足。相比之下,图4b中改进型海绵边界的衰减函数值除了沿y方向呈指数变化外,沿x方向也存在高低相间的周期变化,谷值位置对地震波的衰减能力强于峰值。由于常规海绵吸收边界的衰减能力与峰值的衰减效果相同,因此改进型海绵边界对大角度入射波的总体衰减能力要强于常规海绵吸收边界。

材料力学主要解决三类问题：强度问题、刚度问题和稳定性问题[1-2]。强度是指杆件在外载荷作用下抵抗断裂和过量塑性变形的能力。刚度是指杆件在外载荷作用下抵抗弹性变形的能力。稳定性在材料力学中范围比弹性力学中的窄了很多，特指杆件在轴向压力作用下保持其原有平衡状态的能力。这三类问题反映了固体构件在外载荷作用下力学性能的三个不同的侧面。这三类问题的计算公式大部分情况下可以统一表示为：横截面内力/包含横截面几何性质的参数≤许可量。

3 数值测试

3.1 改进型海绵吸收边界衰减效果测试

改进前、后海绵吸收边界对大角度入射波的衰减效果可以通过对比波场和地震记录来观察和分析。为了不产生额外干扰,我们选择了均匀介质模型,地震波速度vP=3300m/s,vS=1833m/s,介质密度ρ=2800kg/m3,模型的大小为6400m×1000m,离散网格尺寸为10m×10m。数值模拟过程中,为满足稳定性条件,选择的时间采样间隔为0.3ms;震源为P波源,震源子波采用主频为7Hz的Ricker子波。海绵边界衰减函数的参数α=0.04,β=0.20。复合吸收边界由20层平行于边界的网格排列构成,SPML和海绵边界分别占用内层和外层的10层网格。震源设置在接近复合边界的位置(图5中五角星处),以产生大角度边界入射波。

当复合吸收边界使用图4中所示的两种海绵吸收边界的衰减函数时,弹性波数值模拟得到的波场快照在边界处将产生明显差异,如图5所示。使用常规海绵吸收边界时,运算区域的边界处会产生明显的噪声波形,而在改进海绵边界的快照中则较弱(图5中箭头所示位置)。这说明,常规海绵吸收边界对大角度边界入射波的吸收效果弱于改进型海绵吸收边界。

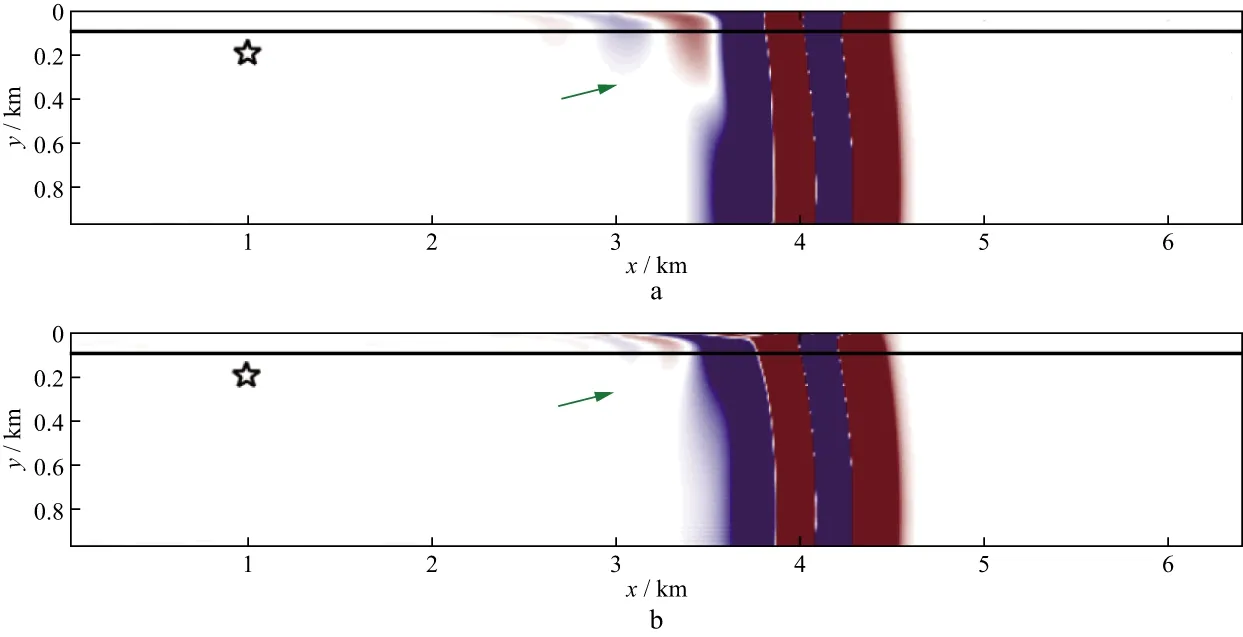
图5 不同海绵吸收边界对应的波场快照(1200ms)(黑线表示吸收边界与正常运算区域的分界线;箭头指出了边界噪声)a 常规海绵吸收边界; b 改进型海绵吸收边界

3.2 复合吸收边界衰减效果测试

为分析复合吸收边界对大角度入射波的衰减效果,本节使用复合吸收边界和SPML边界分别计算地震波场,并对两种情况所获得的地震波场和理论地震记录进行对比分析。我们选择了层状速度模型和Marmousi速度模型分别进行正演模拟和结果分析。

3.2.1 水平层状模型

速度模型中出现较强的速度跳变时,由低速介质中震源发出的地震波入射至高速介质后的传播方向与边界法向夹角较大。图6是一个两层速度模型,其上层和下层的速度分别为3300m/s和1500m/s,纵横波速度比为1.8,介质密度ρ=2800kg/m3。模型被离散化为620×240个规则网格,纵向和横向网格大小均为10m。为满足数值模拟稳定性条件,时间采样间隔采用0.3ms,震源子波采用主频为7Hz的Ricker子波。

图7给出了层状速度模型采用SPML和复合吸收边界得到的水平分量波场快照。由图7可见,使用SPML边界的波场快照在边界附近产生了较强的数值噪声(图7a中箭头所示),产生这种现象的主要原因是地震波大角度入射时,边界处的SPML衰减函数失效,导致地震波未被有效衰减,在边界处产生了数值噪声。在速度分界面处,边界数值噪声的振幅并未出现明显变化,表明这种干扰噪声能够传播至正常运算区域,这对于所要模拟波场的危害很大。随着波传播时间进一步增加,这些数值噪声将透过边界,向正常运算区域内扩散,并与正常地震波混合,降低正演模拟结果的精度。

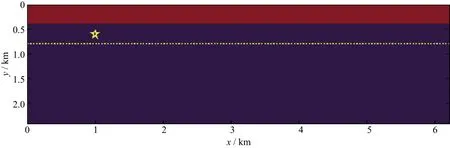
图6 层状速度模型及观测系统(五角星代表震源;虚线代表检波点位置)

图7 层状速度模型采用SPML(a)和复合吸收边界(b)得到的水平分量波场快照(2800ms)(黑色五角星代表震源位置,黑线表示正常运算区域与边界层的分界线)

采用复合吸收边界后,边界处的数值噪声要弱很多,如图7b中箭头所示。虽然在边界层内部存在少量数值噪声,但它们被较好地控制在吸收边界内部,并未明显出现在正常运算区域,因而对正常传播的地震波的干扰可以忽略,有效提高了对大角度入射波的吸收效果。

图8是在平行于边界的地震测线上(图6中虚线)采集到的不同边界条件水平分量地震单炮记录。

图8a显示,SPML吸收边界在较大偏移距处产生了较强的虚假波形(椭圆虚线处所示)。这些虚假波形紧贴边界传播,并有随着偏移距和波传播时间增加而变强的趋势。这种变化趋势与地震波在远偏移距变弱的趋势相反,导致有效地震信号最终被噪声所淹没。由于边界吸收不足进入正常运算区域的噪声不严格遵守正演模拟控制方程,因此随着计算时间的增加,较强的数值噪声会使正演模拟结果变得不稳定[30]。图8b中的地震记录并未出现明显的虚假波形(椭圆虚线处所示),这表明复合边界对大角度入射波进行了有效吸收。这种现象在图8放大后显得尤为突出(图9)。可见,复合吸收边界对大角度入射波的吸收效果要明显优于传统SPML吸收边界,降低噪声的同时提高了计算的精度。

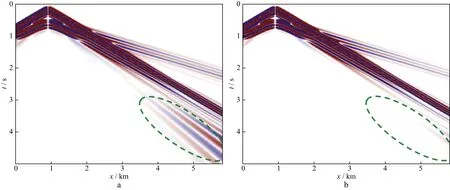
图8 层状速度模型水平分量地震记录(椭圆标出了边界噪声)a SPML边界; b 复合吸收边界

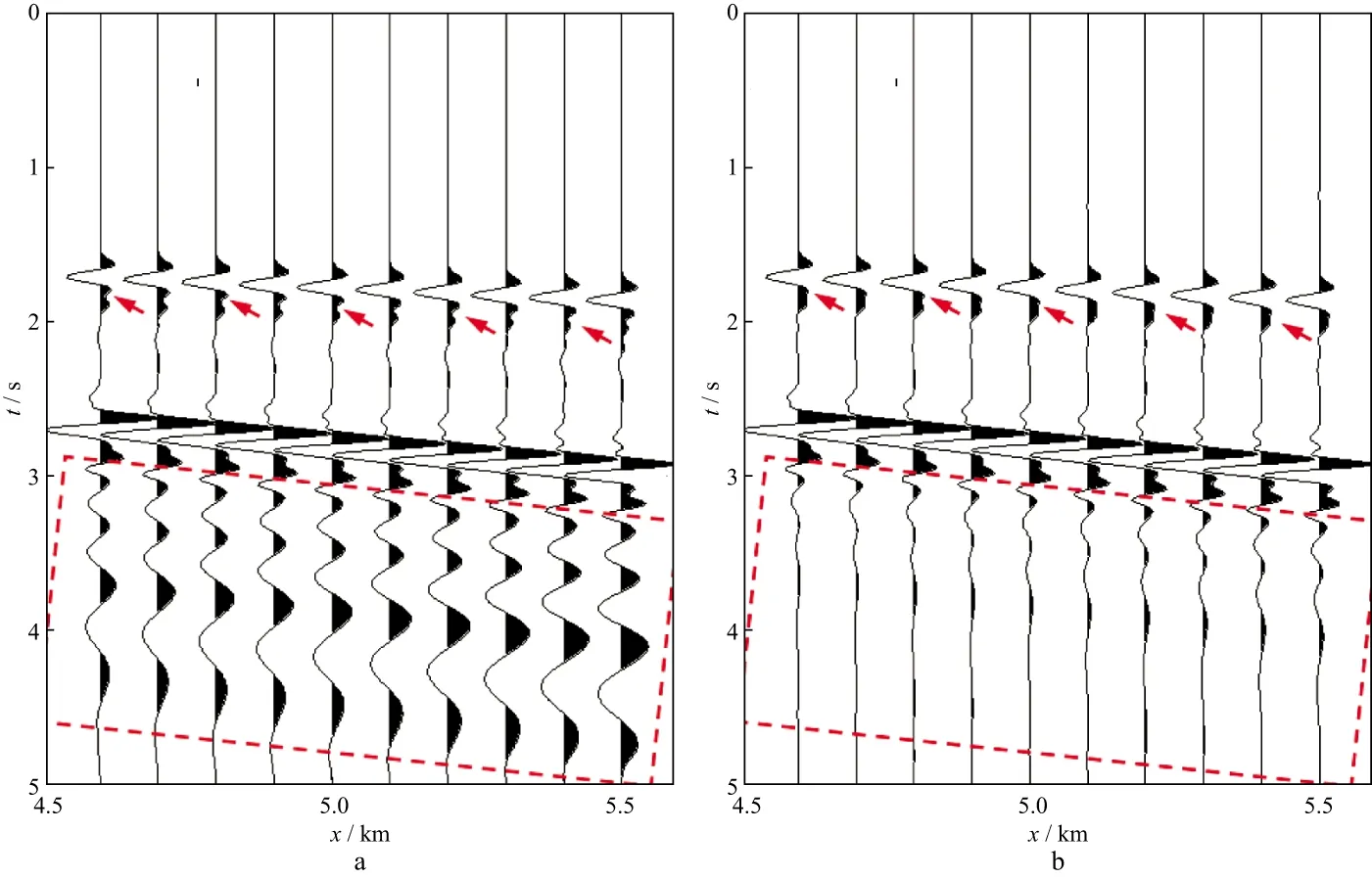
图9 层状速度模型单道地震记录波形对比(所选地震道范围为图8中4.5～5.5km,红色箭头和虚线框指出了数值噪声的位置)a SPML边界; b 复合吸收边界

3.2.2 Marmousi模型

为了进一步测试复合吸收边界在复杂速度模型中的应用效果,采用如图10所示的Marmousi速度模型,纵横波速度比取1.8,介质密度ρ为2800kg/m3。整个空间离散为1149×375个均匀网格,网格大小为20m×20m,数值模拟采用的时间采样间隔为0.3ms,震源子波采用主频为7Hz的Ricker子波,炮检点位置如图10所示。

图10 Marmousi速度模型及观测系统(五角星代表震源;虚线代表测线)

图11给出了Marmousi模型采用不同边界条件得到的波场快照(5600ms)。由图11可见,当地震波接近切向入射到边界时,使用SPML边界的波场快照在边界处出现了数值噪声(图11a中绿色箭头所示),这些数值噪声向正常运算区域内扩散,与正常地震波混合,降低了正演模拟结果的精度。与采用SPML边界的结果不同,采用复合吸收边界后,边界处并未产生明显的数值噪声(图11b中绿色箭头所示)。

吸收边界条件不同所产生的数值噪声的差异也反映在地震记录中。图12是平行于边界地震测线(图10中黄色虚线)的水平分量单炮地震记录。由图12 可见,SPML边界地震记录在5.5s之后存在明显的虚假波形(较强部分如图12a中绿色椭圆处所示),而复合吸收边界的地震记录中未出现明显的虚假波形(图12b中绿色椭圆处所示)。

为对比地震记录的细节,从图12地震记录中抽取10～15km的地震道,并以波形的形式显示,如图13 所示。图13中的波形对比更加明显地展示了SPML边界地震记录中的边界干扰波与模拟所产生的波场重叠,导致部分反射波难以辨别。然而,这种边界干扰波在使用复合吸收边界所得到的地震记录中并不明显。这表明复合吸收边界对于复杂速度模型伪谱法正演模拟产生的边界干扰波也具有较好的吸收效果。

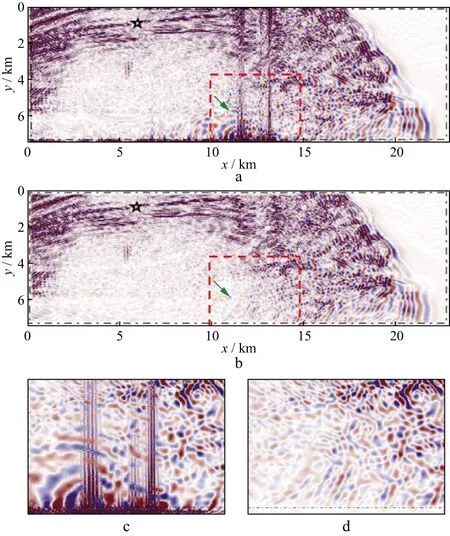
图11 Marmousi模型采用不同边界条件得到的波场快照(5600ms)a SPML边界; b 复合吸收边界; c 图11a中红色虚线窗口放大显示结果; d图11b中红色虚线窗口放大显示结果

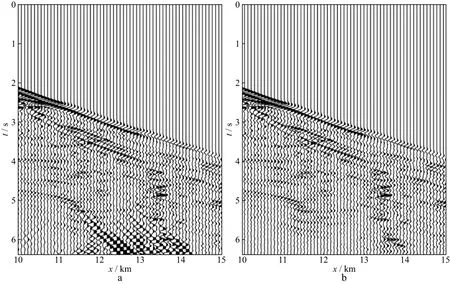
图13 Marmousi模型地震记录波形对比a SPML边界; b 复合吸收边界

4 结论

本文将SPML边界与海绵吸收边界相结合,提出了一种适用于伪谱法弹性波数值模拟的复合吸收边界条件,有效提高了对接近平行于边界传播的大角度边界入射波的吸收能力,并得到如下结论和认识:①理论分析显示,SPML边界对大角度入射波衰减能力不足;②将常规海绵吸收边界的衰减函数由一维变化改进为二维变化可以有效吸收平行于边界传播的地震波;③复合吸收边界继承了SPML对小角度入射波的良好吸收效果,且对大角度入射波的吸收效果优于SPML边界。

本文提出的复合吸收边界数值实现过程较为方便,理论上既可以应用于伪谱法正演模拟,也可以应用于有限差分、有限元等格式的地震波数值模拟中,在不进行复杂数学推导的情况下提高了对边界干扰波的吸收能力。

[1] CLAYTON R,ENGQUIST B.Absorbing boundary conditions for acoustic and elastic wave equations[J].Bulletin of the Seismological Society of America,1977,67(6):1529-1540

[2] 薛东川,王尚旭,焦淑静.起伏地表复杂介质波动方程有限元数值模拟方法[J].地球物理学进展,2007,22(2):522-529

XUE D C,WANG S X,JIAO S J.Wave equation finite-element modeling including rugged topography and complicated medium[J].Progress in Geophysics,2007,22(2):522-529

[3] 李信富,李小凡,张美根.伪谱法弹性波场数值模拟中的边界条件[J].地球物理学进展,2007,22(5):1375-1379

LI X F,LI X F,ZHANG M G.Boundary condition for the pseudo-spectral numerical simulation of seismic wave propagation[J].Progress in Geophysics,2007,22(5):1375-1379

[4] CERJAN C,DAN K,KOSLOFF R,et al.A nonreflecting boundary condition for discrete acoustic and elastic wave equations[J].Geophysics,1985,50(4):705-708

[5] BERENGER J P.A perfectly matched layer for the absorption of electromagnetic waves[J].Journal of Computational Physics,1994,114(2):185-200

[6] 杜增利,徐峰,高宏亮.虚谱法交错网格地震波场数值模拟[J].石油物探,2010,49(5):430-437

DU Z L,XU F,GAO H L.Pseudo-spectral method of the staggered grid seismic wave field numerical simulation[J].Geophysical Prospecting for Petroleum,2010,49(5):430-437

[7] 陈可洋.完全匹配层吸收边界条件研究[J].石油物探,2010,49(5):472-477

CHEN K Y.Study of absorbing condition by perfectly matched layer[J].Geophysical Prospecting for Petroleum,2010,49(5):472-477

[8] HASTINGS F D,SCHNEIDER J B,BROSCHAT S L.Application of the perfectly matched layer (PML) absorbing boundary condition to elastic wave propagation[J].Journal of the Acoustical Society of America,1996,100(100):3061-3069

[9] 王守东.声波方程完全匹配层吸收边界[J].石油地球物理勘探,2003,38(1):31-34

WANG S D.The perfectly matched layer absorbing boundary of acoustic wave equation[J].Oil Geophysical Prospecting,2003,38(1):31-34

[10] CHEW W C,LIU Q H.Perfectly matched layers for elastodynamics:a new absorbing boundary condition[J].Journal of Computational Acoustics,2011,4(4):341-359

[11] 赵海波,王秀明,王东,等.完全匹配层吸收边界在孔隙介质弹性波模拟中的应用[J].地球物理学报,2007,50(2):581-591

ZHAO H B,WANG X M,WANG D,et al.Application of the boundary absorption using a perfectly matched layer for elastic wave simulation in poroelastic media[J].Chinese Journal of Geophysics,2007,50(2):581-591

[12] 高正辉,孙建国,孙章庆,等.基于完全匹配层构建新方法的2.5维声波近似方程数值模拟[J].石油地球物理勘探,2016,51(6):1128-1133

GAO Z H,SUN J G,SUN Z Q,et al.A numerical simulation of the 2.5 dimensional acoustic wave approximate equation based on the perfectly matched absorbing layer[J].Oil Geophysical Prospecting,2016,51(6):1128-1133

[13] 孙林洁,刘春成,张世鑫.PML边界条件下孔隙介质弹性波可变网格正演模拟方法研究[J].石油物探,2015,54(6):652-664

SUN L J,LIU C C,ZHANG S X.A variable grid finite-difference scheme with PML boundary condition in elastic wave of porous media[J].Geophysical Prospecting for Petroleum,2015,54(6):652-664

[14] KRISTEK J,MOCZO P,GALIS M.A brief summary of some PML formulations and discretizations for the velocity-stress equation of seismic motion[J].Studia Geophysica et Geodaetica,2009,53(4):459-474

[15] 张衡,刘洪,李博,等.VTI介质声波方程非分裂式PML吸收边界条件研究[J].石油物探,2016,55(6):781-792

ZHANG H,LIU H,LI B,et al.The research on unsplit PML absorbing boundary conditions of acoustic equation for VTI media[J].Geophysical Prospecting for Petroleum,2016,55(6):781-792

[16] 秦臻,卢明辉,郑晓东,等.弹性波正演模拟中改进的非分裂式PML实现方法[J].应用地球物理,2009,6(2):113-121

QIN Z,LU M H,ZHENG X D,et al.The implementation of an improved NPML absorbing boundary condition in elastic wave modeling[J].Applied Geophysics,2009,6(2):113-121

[17] 秦臻,任培罡,姚姚,等.弹性波正演模拟中PML吸收边界条件的改进[J].地球科学:中国地质大学学报,2009,34(4):658-664

QIN Z,REN P G,YAO Y,et al.Improvement of PML absorbing boundary conditions in elastic wave forward modeling[J].Earth Science:Journal of China University of Geosciences,2009,34(4):658-664

[18] 单启铜,乐友喜.PML边界条件下二维粘弹性介质波场模拟[J].石油物探,2007,46(2):126-130

SHAN Q T,LE Y X.Two-dimensional viscoelastic medium wave field simulation with PML boundary conditions[J].Geophysical Prospecting for Petroleum,2007,46(2):126-130

[19] 张衡,刘洪,李博,等.TTI介质声波方程分裂式PML吸收边界条件研究[J].石油物探,2017,56(3):349-361

ZHANG H,LIU H,LI B,et al.The research on split PML absorbing boundary conditions of acoustic equation for TTI media[J].Geophysical Prospecting for Petroleum,2017,56(3):349-361

[20] MARTIN R,KOMATITSCH D.An unsplit convolutional perfectly matched layer technique improved at grazing incidence for the viscoelastic wave equation[J].Geophysical Journal International,2009,179(1):333-344

[21] RODEN J A,GEDNEY S D.Convolution PML (CPML):an efficient FDTD implementation of the CFS-PML for arbitrary media[J].Microwave & Optical Technology Letters,2015,27(5):334-339

[22] 姜永金,毛钧杰,柴舜连.CFS-PML边界条件在PSTD算法中的实现与性能分析[J].微波学报,2004,20(4):36-39

JIANG Y J,MAO J J,CHAI S L.Implementation and analysis of the perfectly matched layer media with CFS for the PSTD method[J].Journal of Microwaves,2004,20(4):36-39

[23] 张鲁新,符力耘,裴正林.不分裂卷积完全匹配层与旋转交错网格有限差分在孔隙弹性介质模拟中的应用[J].地球物理学报,2010,53(10):2470-2483

ZHANG L X,FU L Y,PEI Z L.Finite difference modeling of Biot’s poroelastic equations with unsplit convolutional PML and rotated staggered grid[J].Chinese Journal of Geophysics,2010,53(10):2470-2483

[24] MARTIN R,KOMATITSCH D,GEDNEY S D.A variational formulation of a stabilized unsplit convolutional perfectly matched layer for the isotropic or anisotropic seismic wave equation[J].Computer Modeling in Engineering & Sciences,2008,37(3):274-304

[25] TOIVANEN J I,STEFANSKI T P,KUSTER N,et al.Comparison of CPML implementations for the GPU-accelerated FDTD solver[J].Progress in Electromagnetics Research M,2011,19:61-75

[26] GAZDAG J.Modeling of the acoustic wave equation with transform methods[J].Geophysics,1981,46(6):854-859

[27] KOSLOFF D.Elastic wave calculation by the Fourier method[J].Bulletin of the Seismological Society of America,1984,74(3):138-142

[28] ZOU Z H,YU W H.Wave field forward modeling and theoretical analysis of weaken in discrete media[J].Applied Geophysics,2006,3(2):75-81

[29] COLLINO F,MONK P B.Optimizing the perfectly matched layer[J].Computer Methods in Applied Mechanics & Engineering,1998,164(1):157-171

[30] COLLINO F,TSOGKA C.Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J].Geophysics,2001,66(1):294-307

[31] 高刚,贺振华,黄德济,等.完全匹配层人工边界条件中的衰减因子分析[J].石油物探,2011,50(5):430-433

GAO G,HE Z H,HUANG D J,et al.Analysis on attenuation factor in the processing of artificial boundary conditions of PML[J].Geophysical Prospecting for Petroleum,2011,50(5):430-433

[32] 周凤玺,张家齐,张海威.完全匹配层中衰减函数的参数优化分析[J].石油物探,2016,55(6):793-799

ZHOU F X,ZHANG J Q,ZHANG H W.The parameter optimization analysis for the attenuation function in the perfectly matched layer[J].Geophysical Prospecting for Petroleum,2016,55(6):793-799

[33] KOMATITSCH D.A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation[J].Geophysical Journal International,2003,154(1):146-153

[34] WENG C C,WEEDON W H.A 3D perfectly matched medium from modified maxwell’s equations with stretched coordinates[J].Microwave & Optical Technology Letters,1994,7(13):599-604

[35] KOMATITSCH D.An un-split convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation[J].Geophysics,2008,73(4):T51-T61