瞬态过程中采煤机机电传动系统动态特性分析

易园园， 秦大同， 刘长钊， 贾涵杰

(重庆大学 机械传动国家重点实验室，重庆 400044)

滚筒式采煤机是机械化、现代化采煤的主要装备，被广泛应用于不同地质条件下的煤炭开采，其性能的优劣直接影响采煤生产率以及企业的经济效益。由于工作环境恶劣和工况复杂多变，采煤机承受强冲击、重载荷，导致传动系统故障率居高不下[1-2]。为适应更加复杂的工作条件，提高可靠性，有必要研究不同工况下采煤机传动系统的动态特性。

目前研究者已对采煤机传动系统展开了广泛研究：刘长钊等[3]通过仿真和试验研究了电动机-齿轮传动系统的连接刚度和阻尼以及齿轮啮合刚度对截割部机电传动系统动力学特性的影响；杨阳等[4]设计了一种机电液短程截割传动系统，并进行了系统调速性能和应对突变工况性能的仿真和效率分析；周笛等[5]基于牵引部传动系统振动响应，研究了系统首次运转和长期运转的可靠性变化规律；张业林[6]分析比较了不同太阳轮故障对截割部行星齿轮机构动态特性的影响；赵丽娟等[7]考虑截割部和牵引部壳体的弹性，采用adams建立了采煤机整机传动系统的刚柔耦合模型，分析了系统在截割含夹矸煤层工况下的振动响应和壳体上应力分布。可以看出，这些研究大多只考虑负载端载荷变化给系统带来的动态激励作用，很少考虑驱动电机动态特性对系统的影响；文献[7]虽然建立了整机机械系统的虚拟样机模型，但是没有考虑截割部和牵引部之间的载荷传递及相互作用。由于实际运行中采煤机由截割电机和牵引电机提供动力，截割部滚筒旋转割煤的同时，通过牵引部行走轮与刮板输送机销排啮合实现向前推进，两者协同作业，共同影响整机的负载状态和振动特性。因此，要系统并全面地了解采煤机传动系统的动态特性，需要将截割部和牵引部的电机-传动系统联合起来进行分析。

本文在考虑电机电磁特性、煤层截割阻抗变化、传动系统扭转振动、时变啮合刚度和齿侧间隙等因素的基础上，建立了采煤机截割-牵引耦合系统机电动力学模型；仿真并分析了系统在启动、滚筒负载突变和截割电机堵转等瞬态过程中的机电动态响应特性，并通过采煤机割煤试验验证了动力学仿真结果的正确性。所得结果为采煤机传动系统的优化设计和整机运行控制奠定了基础。

1 采煤机截割-牵引耦合系统机电动力学模型

1.1 截割部、牵引部机电耦合动力学模型

图1(a)和(b)分别为MG300/700-QWD型电牵引滚筒式采煤机截割部和牵引部的传动系统结构示意，采用集中参数法建立系统纯扭转动力学模型。图中，θi为构件i(i=1，2，…，17，sx，rx，cx，pnx，j，d，q，b)的转角，θi=φi+φi，φi是构件i的刚体转动角位移，φi是构件i的扭转振动角位移。kN和cN分别为轴N(N=1，2，…，10)的扭转刚度和扭转阻尼；yb为机身位移；mb为整机质量；Ji为构件i的转动惯量；Td为滚筒负载转矩；Fb为单侧牵引阻力。

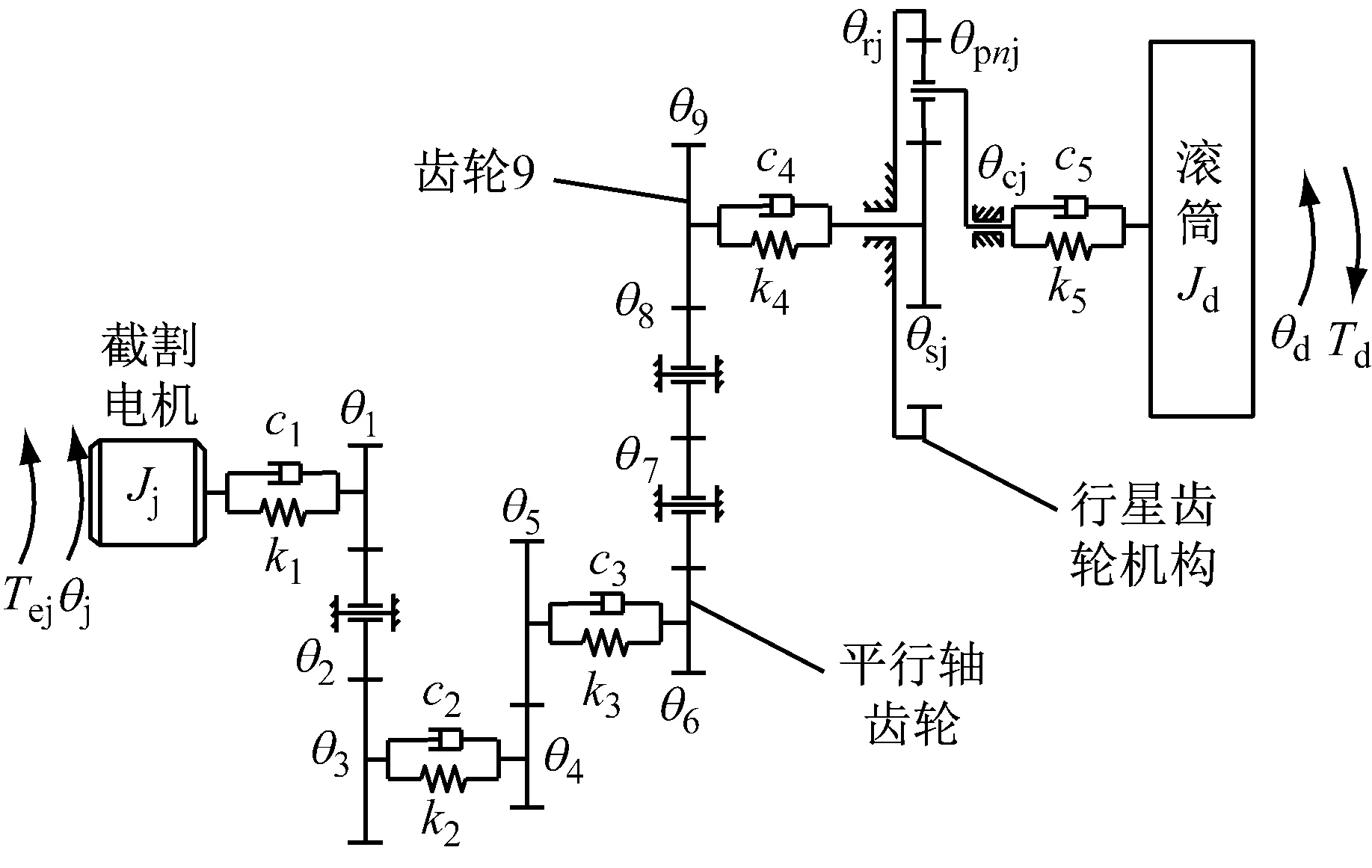
(a) 截割部传动系统动力学模型

(b) 牵引部传动系统动力学模型

区别于以往研究者采用集中参数法建立的齿轮系统振动模型[8]，本文基于Liu等[9]的研究，依据牛顿第二定律建立截割部和牵引部传动系统的扭转振动-转动动力学模型，以便考虑驱动电机的转速变化特性对传动系统振动响应的影响。建立的传动系统中各类型构件的动力学方程如式(1)～式(4)。

行星齿轮机构的动力学方程

(1)

平行轴齿轮副的动力学方程

(2)

滚筒d的动力学方程

(3)

机身b的动力学方程

(4)

式中：下标s、r、c、pn分别表示太阳轮、齿圈、行星架、第n个行星轮；下标x=j、q，分别对应截割部和牵引部；F、r、α分别为齿轮副啮合力、齿轮基圆半径、啮合角；TN和TN+1分别为轴N和轴N+1承受的转矩；krtx和crtx分别为齿圈的切向支撑刚度和支撑阻尼；rcx为行星轮中心分布圆的半径；下标i、i+1、i-1分别表示齿轮i以及与之相邻的齿轮；ui、vi取值随齿轮i在传动系统中所处的位置而定，可取0或1。

将式(1)、(2)、(3)和式(1)、(2)、(4)分别通过各构件之间的传动轴建立联系并组装，可分别得到截割部和牵引部传动系统矩阵形式的弹性动力学方程

(5)

(6)

式中：Q、M、C、K、F分别为系统广义坐标向量、质量矩阵、阻尼矩阵、刚度矩阵和外载荷向量；下标j、q分别对应截割部和牵引部。

截割电机和牵引电机均采用鼠笼式三相异步电动机。在dq坐标系建立三相异步电机动态数学模型[10]，其等效电路如图2所示，其电压方程、磁链方程、电磁转矩方程如式(7)。

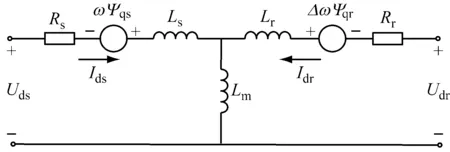
(a) d轴电路

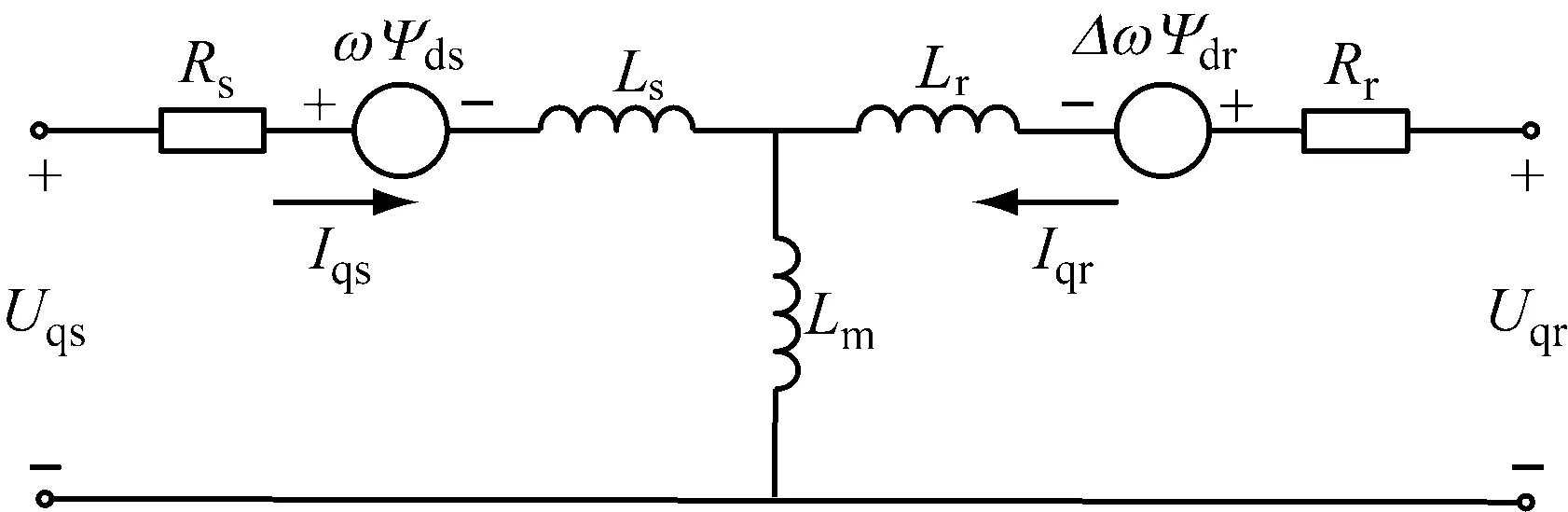
(b) q轴电路

Tex=1.5p(ΨdsIqs-ΨqsIds)

(7)

电机和传动系统之间通过电机轴连接，存在如图3所示的耦合关系，其对应的关系式如式(8)、(9)。将式(5)、(7)、(8)和式(6)、(7)、(9)分别组装在一起，可分别得到截割部和牵引部的机电耦合动力学模型。

图3 电机和传动系统耦合关系

(8)

(9)

式中：Tex为电机电磁转矩，x=j，q，分别对应截割部和牵引部；T1、T6分别为截割电机轴和牵引电机轴的负载转矩。

1.2 截割-牵引耦合系统动力学模型

采煤机截割部滚筒旋转割煤的同时，通过牵引部向前推进，根据其工作原理可知，截割部和牵引部之间存在如图4所示的运动学耦合关系：滚筒转速和牵引速度共同决定了截齿切削厚度，而截齿切削厚度影响滚筒负载转矩和牵引阻力，进而影响截割部和牵引部传动系统的振动响应。

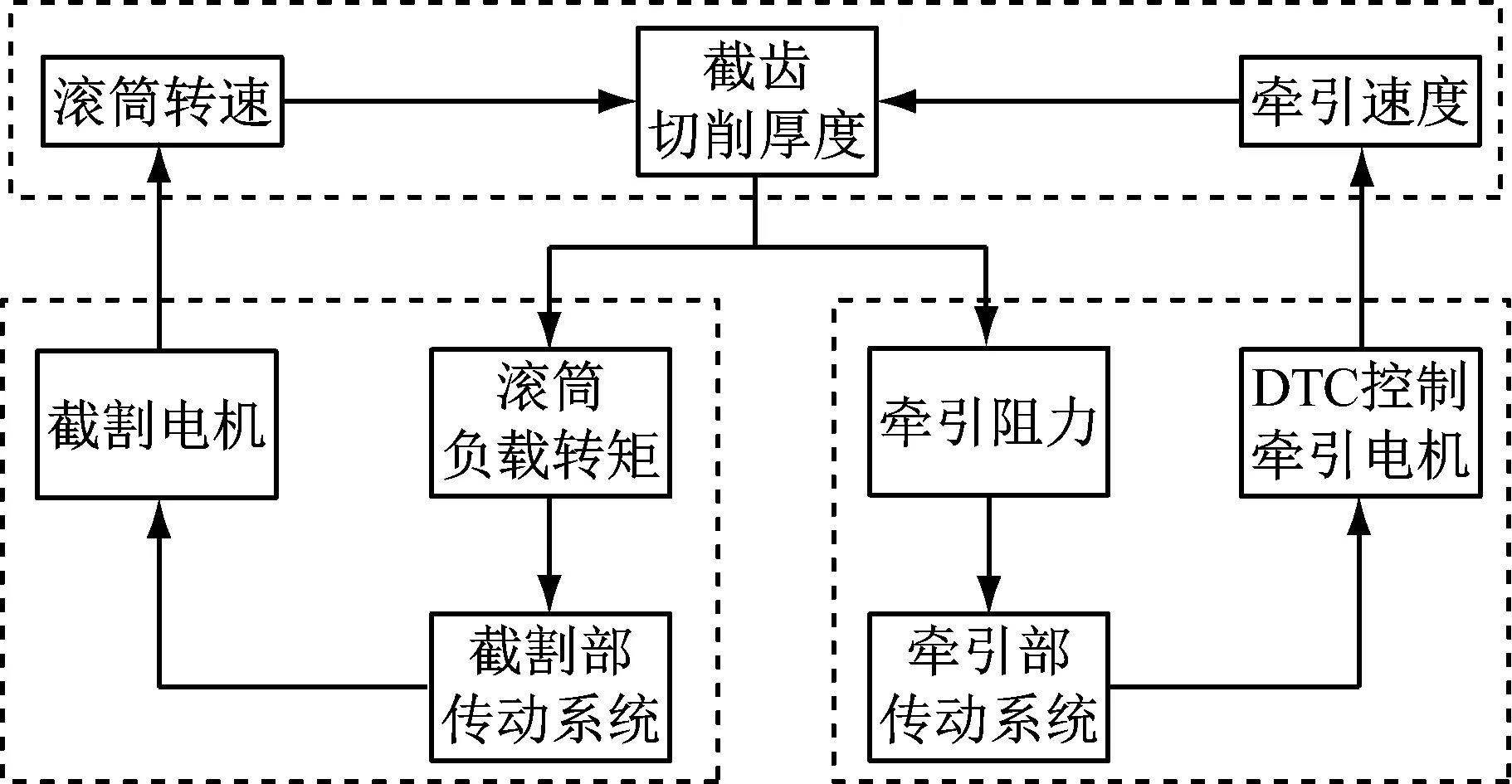
图4 截割部和牵引部的耦合作用关系

Fig.4 Coupling relationship between the cutting unit and the haulage unit of a coal shearer

其中，截齿平均切削厚度hz[11]、截齿平均截割阻力Fz、滚筒负载转矩Td以及单侧牵引阻力Fb[12]的计算式分别为

(10)

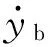
通过式(10)将式(5)中的变量θd和式(6)中的变量yb建立联系，可将截割部和牵引部关联起来，联立式(5)至式(10)从而得到采煤机截割-牵引耦合系统模型。

2 系统内部载荷和边界条件

2.1 齿轮副啮合力

基于Liang等[13]的研究，采用能量法计算直齿轮副啮合刚度，然后表示成傅里叶级数的形式。以往研究者大多将啮合刚度设定为时间的函数，这需要预先知道齿轮转速随时间的变化规律，当传动系统在电机的驱动下作变转速运动时，啮合刚度的周期具有随机性和时变性，不宜再采用时间表示；而不论转速是否变动，可以认为啮合刚度始终随齿轮转角周期性变化，因此本文将啮合刚度表示成齿轮副中主动轮转角θp的函数，即

(11)

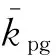
Kahraman等[14]已经证明了可以忽略啮合阻尼的时变性，因此将齿轮副啮合阻尼的计算式[15]表示为

(12)

式中：ζpg为啮合阻尼比，本文取为0.07；mp和mg分别为主、从动轮的质量。

考虑齿轮副工作面接触、分离和非工作面接触等非线性啮合状态，其啮合线方向如图5所示。

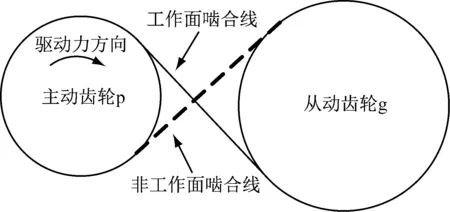
图5 齿轮副啮合线方向

为区别啮合状态，定义工作面接触时啮合力为正值，非工作面接触时啮合力为负值，并考虑非工作面接触时啮合刚度的相位差[16]，则一对齿轮的法向啮合力为

δpg=rpθp-rgθg

(13)

式中:b是齿侧间隙；δpg是啮合线上两齿轮的相对位移；rp和rg分别为主、从动轮的基圆半径。

2.2 轴传递的转矩

轴N的扭转刚度和扭转阻尼的计算式[17]分别为

(14)

则轴N所传递的转矩计算式为

(15)

2.3 各种工况施加的边界条件

考虑采煤机工况条件的复杂性和多变性，选择电机启动、滚筒负载突变和截割电机堵转等工况进行研究。各种工况制定的边界条件如下：

电机启动工况：令煤层截割阻抗为0，截割电机采用直接启动方式，牵引电机采用变频启动，变频器设定的电机转速变化率为300 r/min/s，目标牵引速度为4 m/min。

滚筒负载突变工况：通过牵引电机变频器设定牵引速度为6 m/min，令煤层截割阻抗在2 s时由220 kN/m突增为300 kN/m，以模拟滚筒由软煤层截割到硬煤层时系统受到的冲击。

截割电机堵转工况：令煤层截割阻抗在2 s时由220 kN/m突增为660 kN/m，使滚筒负载转矩由额定值突变为额定值的3倍，以模拟滚筒被煤岩卡死时系统的动态特性。

3 不同工况仿真结果分析

根据前面建立的数学模型，在MATLAB /Simulink仿真平台搭建截割-牵引耦合系统的仿真模型。牵引电机采用由仿真平台提供的DTC变频调速电机模块，使用的主要技术参数见表1。针对不同工况，对模型施加相应的边界条件，并采用4-5阶Runge-Kutta算法进行求解。

表1 采煤机主要参数

3.1 电机启动

图6给出的分别是启动过程中截割电机和牵引电机的转速和电磁转矩。由于启动时滚筒负载转矩为零，截割电机只需提供加速力矩拖动传动系统和滚筒升速至最大值，之后电磁转矩恢复到零附近。而受机身自重引起的摩擦力影响牵引阻力不为零，因此牵引电机需提供加速力矩和克服牵引阻力的力矩，待牵引速度达到目标值后加速力矩消失，牵引阻力不变。

(a) 截割电机转速和电磁转矩

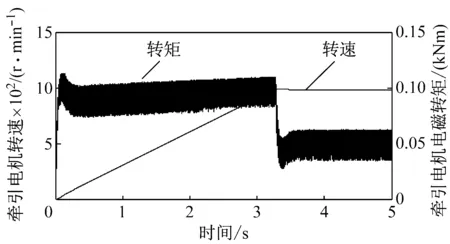
(b) 牵引电机转速和电磁转矩

在截割电机启动初始阶段，电磁转矩发生剧烈振荡，振荡频率为50 Hz，幅值达到电机额定转矩的2.3倍，给电机带来较大冲击。这与文献[18-19]中异步电机启动试验及仿真所得结果类似，验证了本文所建电机模型的正确性。相比之下，牵引电机启动过程则要平稳得多，电磁转矩最大值仅为额定值的0.42倍。可知，由于启动方式不同，截割电机和牵引电机在启动阶段受到的冲击也不同；为减小启动冲击，截割电机可尝试采用减压启动、软启动等方式[20]。

图7所示分别为电机启动过程中截割部和牵引部传动系统中齿圈-行星轮啮合刚度、啮合力及其时频分布。在截割电机启动初期，电磁转矩高频振荡使截割部齿圈-行星轮发生连续的脱啮现象，但由于滚筒的转动惯量较大，使电机转速波动较小，脱啮引起的单边冲击力并不大；在截割电机转速达到最大值后，电磁转矩在恢复至零的过程中再次产生波动，使截割部齿圈-行星轮发生双边冲击现象，将给采煤机系统带来振动噪声；直到电机转速达到稳定，传动系统处于轻载状态，此时再次发生脱啮现象，但冲击力幅值较小。相比之下，牵引部传动系统在经历启动冲击之后快速进入平稳运行状态。从时频图可以看出，随着电机转速升高，传动系统啮合频率及其倍频呈逐渐增大趋势；1倍啮合频率对应的幅值较大，在时频图中颜色较深，而高次谐波的幅值较小，在时频图中颜色较浅。

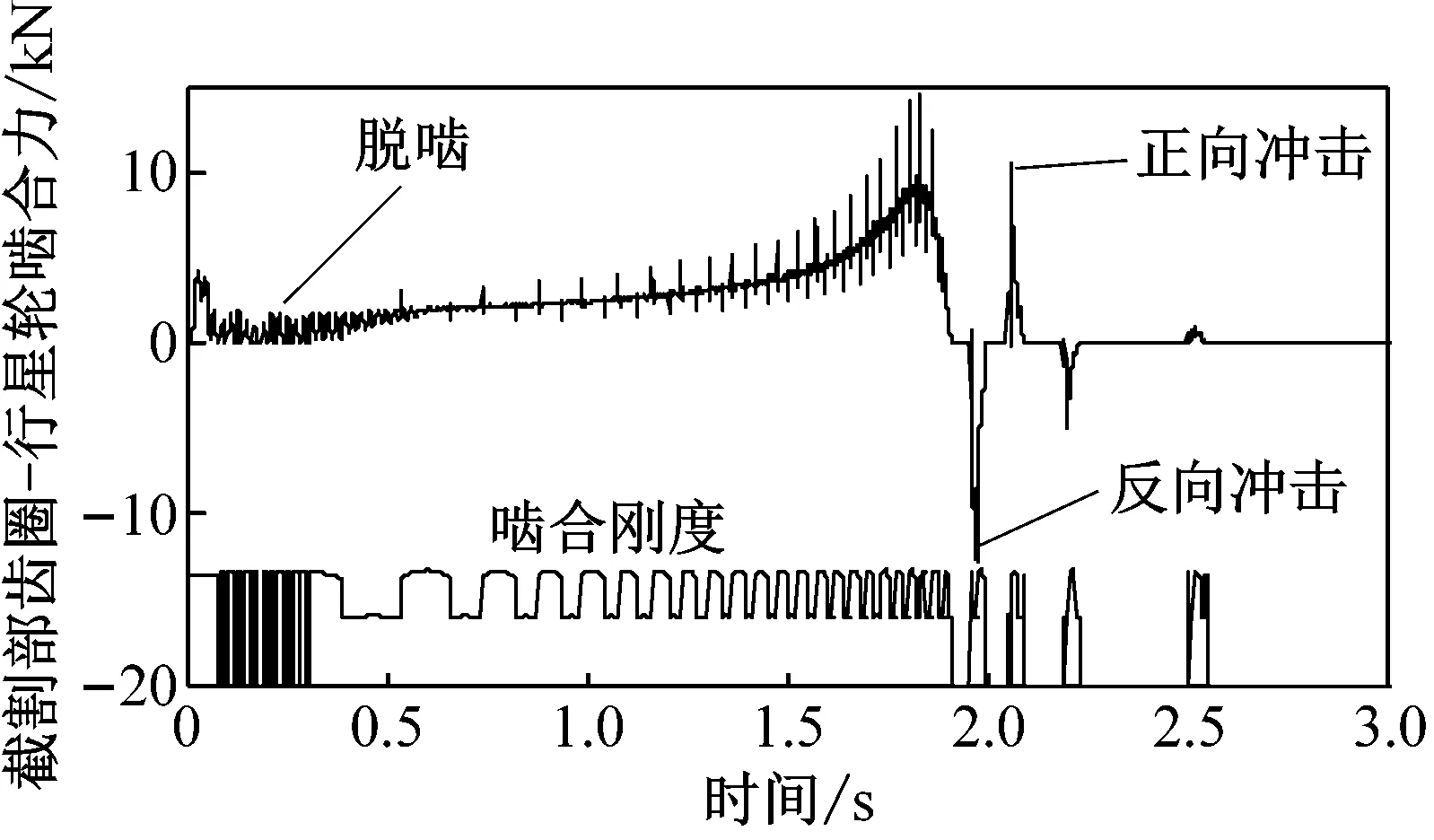
(a) 截割部齿圈-行星轮啮合力和啮合刚度

(b) 截割部齿圈-行星轮啮合力的时频分布

(c) 牵引部齿圈-行星轮啮合力和啮合刚度

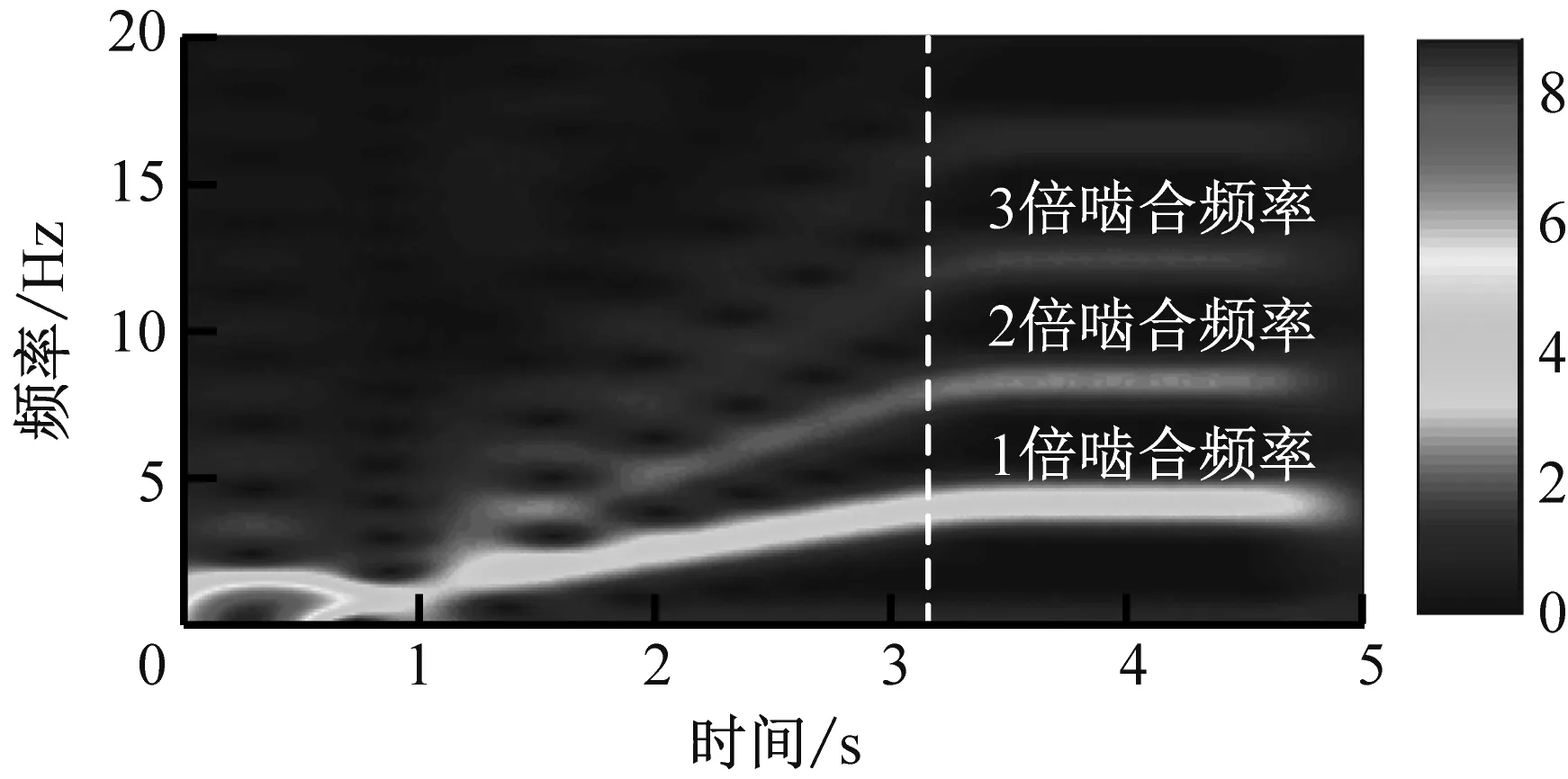
(d) 牵引部齿圈-行星轮啮合力的时频分布

图7 启动时传动系统动态特性

Fig.7 Dynamic behavior of the transmission systems in the run-up regime

3.2 滚筒负载突变

图8所示分别为滚筒负载突变时截割电机和牵引电机电流有效值的变化。从图中标明的数值可以看出：当煤层截割阻抗在2 s时由220 kN/m增大36%到300 kN/m后，截割电机电流由177.4 A增大34%到237.4 A，而牵引电机电流由41.5 A增大16%到48.3 A；表明截割阻抗突增后滚筒负载比牵引阻力增大的幅度更大。从式(10)可以看出，这是由于滚筒负载与截割阻抗基本成正比例关系，而牵引阻力包含机身重量贡献量和滚筒负载贡献量两部分，使牵引阻力受外界扰动的影响较小。因此在设计采煤机时，为保证系统的可靠性，截割部(包括传动系统、电机、壳体等)应比牵引部取更大的使用系数。

图8 滚筒负载突变时电机电流有效值

Fig.8 RMS current of the motors during the sudden change of the drum load

图9所示分别为滚筒负载突变时截割部齿轮9(如图1(a)中所指)和牵引部行走轮的振动加速度均方根值的变化。截割阻抗增大后，滚筒负载和牵引阻力均随之增大，使截割部和牵引部传动系统的振动加剧。表明通过监测电流和振动信号都可以反馈采煤机的负载状态，当监测到系统过载时，应对采煤机进行调速降载以保护传动系统。

图9 滚筒负载突变时传动系统动态特性

Fig.9 Dynamic behavior of the transmission systems during the sudden change of the drum load

3.3 截割电机堵转

图10给出的分别是截割电机堵转时电机的转速、电磁转矩和电流有效值、截割部齿圈-行星轮啮合力及啮合刚度。当煤层截割阻抗在2 s时由220 kN/m增大到660 kN/m后，负载转矩超过了截割电机允许的最大过载转矩，截割电机转速和电磁转矩快速下降，电流快速增大；在此过程中截割部传动系统承受约0.5 s的极限载荷，这要求传动系统具有足够的过载能力。0.5 s后，截割电机转速在零附近波动，使传动系统发生双边冲击现象；最终系统停止转动，电机电磁转矩和传动系统内部载荷降低，但电流增大为原来的3.68倍。这与文献[21]中异步电机堵转仿真结果类似，验证了本文结果的正确性。堵转之后若不及时断开截割电机的电源开关，电机有可能因电流过大而被烧毁，所以应在电路中装设过流保护装置。

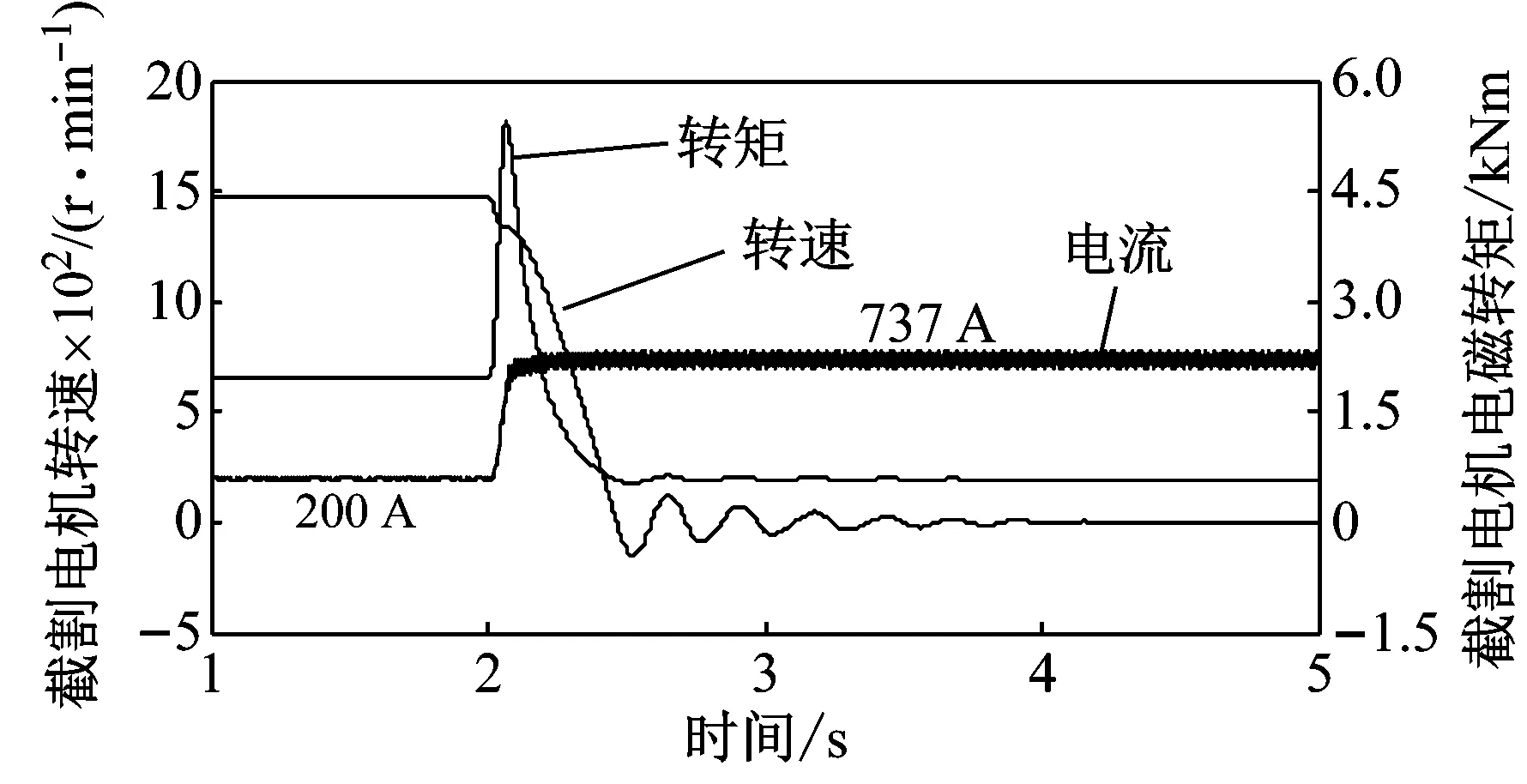
(a) 截割电机的转速、电磁转矩和电流有效值

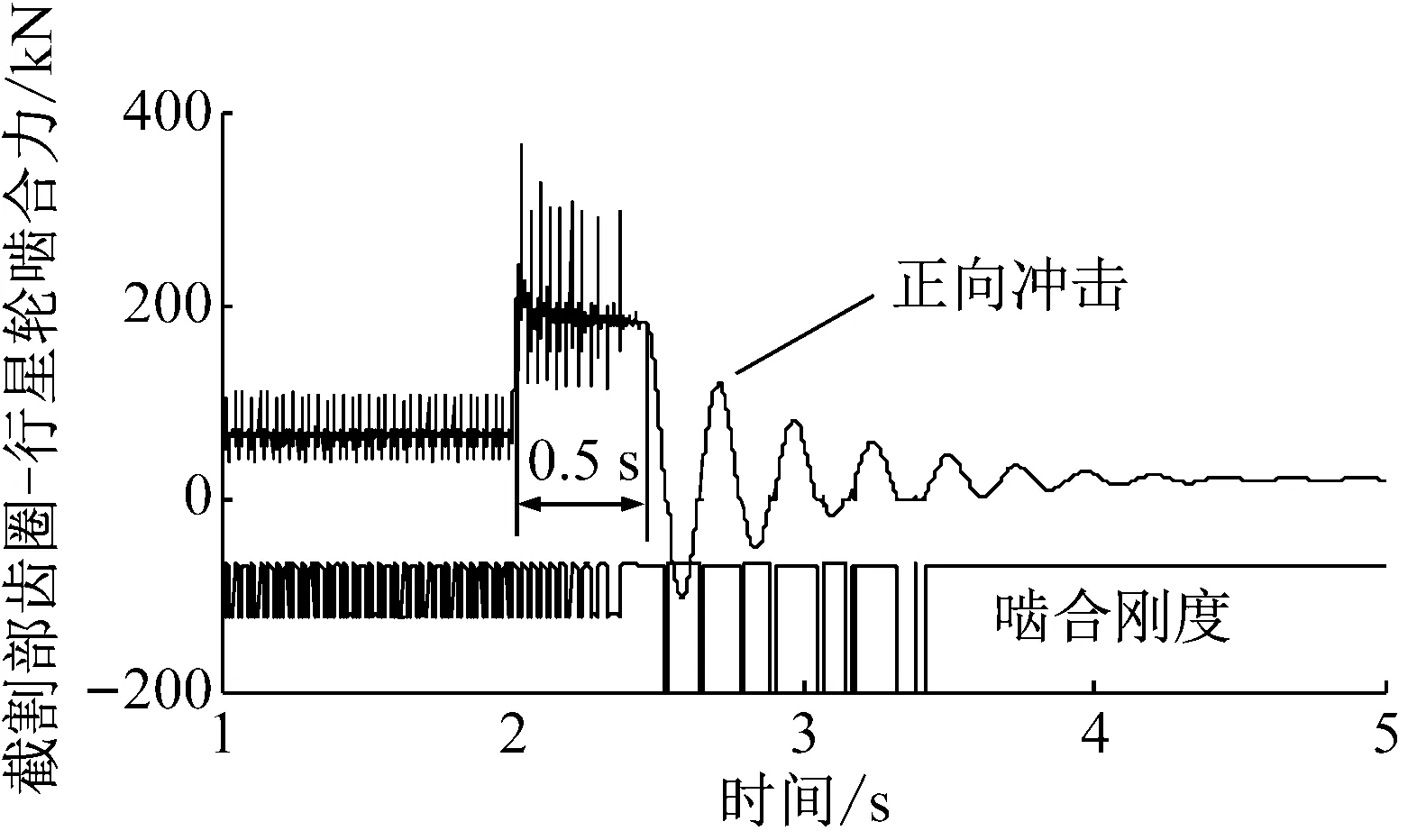
(b) 截割部齿圈-行星轮啮合力和啮合刚度

Fig.10 Electromechanical dynamic behavior of the system in the locked-rotor regime

使用系数KA是考虑由于原动机和工作机械的载荷变动、冲击、过载等对齿轮产生的外部附加动载荷的系数[22]。定义齿轮副的使用系数KA的计算式[23]为

(16)

图11所示为滚筒受到冲击载荷瞬间从电机端到滚筒端各级齿轮副的使用系数。可以看出，越靠近电机端，齿轮副的使用系数越大，表明高速级齿轮受滚筒上冲击载荷的影响比低速级要大，因此在设计传动系统时高速级应取较大的安全系数。

4 采煤机割煤试验

为验证动力学仿真结果的正确性，在试验用采煤机上进行截割试验，利用煤层厚度突变来实现滚筒负载突变工况。试验装置及传感器布置如图12所示，在截割部齿轮9和牵引部行走轮的轴承座附近壳体上分别布置振动加速度传感器，采用LMS Test.Lab数据采集系统实时采集振动信号，并对传感器及数据采集装置采取必要的防护措施。

图11 冲击瞬间各级齿轮副的使用系数

Fig.11 Application factors for every stage of gear pair in the impact moment

(a) 模拟负载突变的煤壁

(b) 振动加速度传感器布置

图13给出了通过电流传感器读取的截割电机和牵引电机电流以及测得的传动系统振动加速度均方根值的变化曲线。煤层厚度增大后，截割电机电流变为原来的1.3倍，而牵引电机电流变为原来的1.1倍；表明截割部受外界扰动的影响比牵引部更大，与根据图8所得结论一致。通过与图8、图9对比可知，仿真和试验获得的电信号和振动信号变化趋势相似(幅值差别较大的原因：一是试验用机和本文仿真对象机型的型号不同，二是考虑试验成本，试验时采煤机滚筒割煤深度较浅，而本文模拟的是滚筒满负荷运行工况)，验证了本文所建截割-牵引耦合模型的可行性和仿真结果的正确性。

(a) 截割电机和牵引电机电流实测值

(b) 截割部和牵引部传动系统振动加速度实测值

Fig.13 RMS current and vibration acceleration signals measured from the experiment

5 结 论

(1) 考虑电机电磁特性、煤层截割阻抗变化、传动系统扭振、时变啮合刚度和齿侧间隙等因素，采用MATLAB /Simulink搭建了采煤机截割-牵引耦合系统机电动力学模型；仿真并分析了系统在启动、滚筒负载突变和截割电机堵转等瞬态过程中的机电动态响应特性，并进行采煤机割煤试验验证了仿真结果的正确性。

(2) 在截割电机启动和堵转过程中，电磁转矩剧烈变化使电机和传动系统之间发生强烈的耦合作用，导致传动系统出现脱啮、反冲等非线性冲击现象，使传动系统振动噪声增大；为保护电机和传动系统，应避免频繁启停电机，加设过流保护装置，提高传动系统的过载能力。

(3) 滚筒负载突变给采煤机系统带来较大的外部冲击，且冲击载荷在截割部和牵引部之间相互传递，使整机传动系统振动加剧；为保证系统可靠性，在设计采煤机传动系统时，截割部应比牵引部取更大的使用系数，高速级齿轮应比低速级取更大的安全系数。

[1] 周久华，米林. 采煤机摇臂齿轮箱故障与可靠性分析[J]. 神华科技，2011, 9(3):39-41.

ZHOU Jiuhua, MI Lin. Ranging arm gearbox fault analysis of shearer and its reliability analysis [J]. Shenghua Technology, 2011, 9(3): 39-41.

[2] 宋相坤，胡俊，朱信平. 复杂地质条件下大功率采煤机行走系统常见故障与对策[J]. 煤矿机械，2014, 35(11): 288-290.

SONG Xiangkun, HU Jun, ZHU Xinping. Common faults and measures of high-power shearers running system under complex geological condition[J]. Coal Mine Machinery, 2014, 35(11): 288-290.

[3] 刘长钊，秦大同，廖映华. 采煤机截割部机电传动系统动力学特性分析[J]. 机械工程学报，2016, 52(7): 14-22.

LIU Changzhao, QIN Datong, LIAO Yinghua. Dynamic analysis for the cutting electromechanical transmission system in the long-wall shearer[J]. Journal of Mechanical Engineering, 2016, 52(7): 14-22.

[4] 杨阳，邹佳航，秦大同，等. 采煤机高可靠性机电液短程截割传动系统[J]. 机械工程学报，2016, 52(4): 111-119.

YANG Yang, ZOU Jiahang, QIN Datong, et al. High reliability electromechanical-hydraulic short-range cutting transmission system of shearer[J]. Journal of Mechanical Engineering, 2016, 52(4): 111-119.

[5] 周笛，张旭方，杨周，等. 采煤机牵引部传动系统动态可靠性分析[J]. 煤炭学报，2015, 40(11): 2546-2551.

ZHOU Di, ZHANG Xufang, YANG Zhou, et al. Vibration reliability analysis on tractive transmission system of shearer[J]. Journal of China Coal Society, 2015, 40(11): 2546-2551.

[6] 张业林. 采煤机摇臂传动系统动力学及传感器优化布置研究[D]. 徐州：中国矿业大学，2014: 26-46.

[7] 赵丽娟，田震. 薄煤层采煤机振动特性研究[J]. 振动与冲击，2015, 34(1): 195-199.

ZHAO Lijuan, TIAN Zhen. Vibration characteristics of thin coal seam shearer[J]. Journal of Vibration and Shock, 2015, 34(1): 195-199.

[8] KHABOU M T, BOUCHAALA N, CHAARI F, et al. Study of a spur gear dynamic behavior in transient regime[J]. Mechanical Systems and Signal Processing, 2011, 25(8): 3089-3101.

[9] LIU C, QIN D, LIM T C, et al. Dynamic characteristics of the herringbone planetary gear set during the variable speed process[J]. Journal of Sound and Vibration, 2014, 333(24): 6498-6515.

[10] 韩如成，潘峰，智泽英. 直接转矩控制理论及应用[M]. 北京：电子工业出版社，2012:31-35.

[11] 刘春生，于信伟，任昌玉. 滚筒式采煤机工作机构[M]. 哈尔滨：哈尔滨工程大学出版社，2010: 13-20.

[12] 王丹玉，王启佳，孙维. 采煤机牵引速度的分析与选择[J]. 煤矿机械，2012, 33(10): 195-197.

WANG Danyu, WANG Qijia, SUN Wei. Analysis and selection of shearer haulage speed[J]. Coal Mine Machinery, 2012, 33(10): 195-197.

[13] LIANG X, ZUO M J, PATEL T H. Evaluating the time-varying mesh stiffness of a planetary gear set using the potential energy method[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2014, 228(3): 535-547.

[14] KAHRAMAN A, SINGH R. Interactions between time-varying mesh stiffness and clearance non-linearities geared system[J]. Journal of Sound and Vibration, 1991, 146(1): 135-156.

[15] LIANG X, ZUO M J, HOSEINI M R. Vibration signal modeling of a planetary gear set for tooth crack detection[J]. Engineering Failure Analysis, 2015, 48(11): 185-200.

[16] GUO Y, PARKER R G. Analytical determination of back-side contact gear mesh stiffness[J]. Mechanism and Machine Theory, 2014, 78(4): 263-271.

[17] 张策. 机械动力学[M]. 北京：高等教育出版社，2008: 300-340.

[18] 闻邦椿，顾家柳，夏松波，等. 高等转子动力学[M]. 北京：机械工业出版社，1999: 228-242.

[19] 续艳珍，王建民. 异步电动机起动过程中转轴上的扭矩振荡现象研究[J]. 中小型电机，2005, 32(5): 10-13.

XU Yanzhen, WANG Jianmin. Study on torsional torque oscillation in starting process of induction motor[J]. S&M Electric Machines, 2005, 32(5): 10-13.

[20] 顾绳谷. 电机及拖动基础[M]. 北京：机械工业出版社，2007:111-115.

[21] 张强，王海舰，毛君，等. 刮板输送机系统机电耦合模型及仿真分析[J]. 中国机械工程，2015, 26(23): 3134-3139.

ZHANG Qiang, WANG Haijian, MAO Jun, et al. Electromechanical coupling modeling and simulation analysis of scraper conveyor system[J]. China Mechanical Engineering, 2015, 26(23): 3134-3139.

[22] 闻邦椿. 机械设计手册[M]. 北京：机械工业出版社，2014:47-48.

[23] WEI J, LÜ C, SUN W, et al. A study on optimum design method of gear transmission system for wind turbine[J]. International Journal of Precision Engineering and Manufacturing, 2013, 14(5): 767-778.