含铰可展桁架结构非线性模型修正方法研究

宋正华， 姜 东， 曹芝腑， 韩晓林， 费庆国

(1. 东南大学 工程力学系， 南京 210096； 2. 南京林业大学 机械电子工程学院， 南京 210037)

在空间站建设、深空探测等航天任务中，大型桁架式可展结构得到了广泛的应用，例如卫星天线的支撑结构、柔性太阳能帆板的展开支撑臂等结构[1-2]。可展结构各部件之间通过铰链来连接，例如，美国NASA用于航天飞机对地进行高分辨率观测的ADAM支撑臂全部展开长60 m，由87个桁架单元构成，含有696个铰链[3]。铰链中存在间隙，在外载荷作用下会发生摩擦和碰撞等非线性现象，对结构的工作精度和抗干扰能力产生不利影响。因此，铰链对结构动力学特性的影响不可忽视，需要对铰链的力学特性展开研究，为设计提供可靠的评价和参考。国内外学者围绕含铰结构开展了相关的研究：Ferney等[4-5]基于力状态映射方法进行铰链的实验研究，Tomihiko等[6-7]通过实验建立了铰链的非线性刚度和阻尼模型；Webster等[8-9]基于描述函数法、残余力法和谐波展开法等进行非线性力描述，利用有限单元法进行了无约束含铰链结构的动力学分析；黄铁球等[10]对铰链的物理模型进行分析，得出了铰间相互作用力的关系，并通过建立有限单元模型得到了桁架结构的非线性动力学模型；陈鹿民等[11]设计了一个动力型桁架式可展结构，并对其进行了动力学实验研究；尉立肖等[12]研究圆柱副间隙结构的间隙接触碰撞模式，对曲柄结构进行了动力学仿真；阎绍泽等[13]研究碰撞及摩擦力对可展结构动力学性能的影响。然而，对于非线性结构的反问题的研究还较少，由于动力学反问题的研究是建立准确的结构有限元模型和结构优化设计的重要环节，所以对非线性结构的反问题的研究也相当重要。

目前，有限元模型修正方法基本都是建立在线性结构基础之上[14]，但是实际工程当中，振动结构都是非线性的，线性只是在一定条件下的近似。当非线性比较明显时，一般的线性模型修正方法不再适用，所以对非线性结构模型修正方法的研究也相当重要。费庆国等[15]提出了基于神经网络的非线性结构的修正方法，并将此方法应用到了非线性梁结构的有限元模型修正；Tang等[16]提出了主要针对可积非线性系统参数识别的时域方法和相平面法。Peng[17]提出利用一次近似频率响应方程来识别弱非线性的单自由度振动系统参数的新方法。Yasuda[18]提出一种识别非线性多自由度系统的频域方法。马睿等[19]提出了一种柔性结构动力学模型修正方法，并将此方法运用于在地面模态试验中由于重力而产生几何非线性的太阳翼结构。

本文将描述函数法运用到含非线性铰链的桁架结构的建模当中，采用谐波平衡法分析了含铰结构的非线性动态特性，实现了空间含铰结构动态建模及计算。在动响应分析基础上，运用模式搜索法对可展结构铰链的非线性刚度进行了模型修正的研究。

1 模型修正理论基础

根据修正过程中使用实验数据的不同，现有的模型修正方法可以大致分为基于模态参数的模型修正方法和基于频响函数的模型修正方法两大类，近年来也出现了基于时域相应的修正方法。但是对于非线性结构来说，已经不存在线性系统中的模态概念，所以常见的是基于频响函数的修正方法。基于频响函数的修正计算的频率范围宽，采用适当数目频率点上的频响函数，便可求解问题，是结构动力学参数修正领域有发展前景的方法之一。

首先，定义结构位移响应的试验测试值与谐波平衡法计算值的差值为残差项Δ(P)

Δ(P)=HE(ω)-HA(ω,P)

(1)

式中：参数P代表需要识别的n个非线性参数向量，即P=[p1，p2，…，pn]；HE、HA分别代表响应的实验值和计算值，根据最小二乘原则，若要计算所得的频响函数能够最佳拟合试验结果

(2)

目标函数应最小，这便是基于频响函数的参数识别方法的基本思路。试验中，一般得不到幅频曲线的解析表达式，而是离散的数据点，假设试验选取的频率点为ω1，ω2，…，ωn，代入式(2)可得：

(3)

则将修正问题转化成为无约束最优化问题。若能在参数P的合理取值范围[P1，P2]内找到一个值Pa，使得目标函数R(P)取极小值，则Pa为待修正参数的精确值。对于含铰链的非线性系统，频响函数通过数值方法求解获得，故目标函数R(P)也是数值函数。对于桁架结构的模型参数修正，先进行非线性响应计算得到频响函数，然后与实验数据一起构造残差函数，运用模式搜索法搜索残差函数值最小时的参数值，即为修正后的模型参数。

2 非线性模型修正流程

对无约束最优化问题来说，可以有多种直接搜索方法，模式搜索法是一种直接搜索优化方法，其基本原理就是寻找一系列的点x0，x1，x2…，这些点都越来越靠近最优值点，当搜索进行到终止条件时则将最后一个点作为本次搜索的解，一般不需要求解目标函数中的任何导数信息，仅对目标函数极值进行模式移动和探测移动搜索。在MATLAB中已经有相关工具箱，调用pattern-search函数可以使用模式搜索法解决相关最优化问题。利用模式搜索法的非线性结构模型修正方法流程图见图1，图中FRF指频响函数。

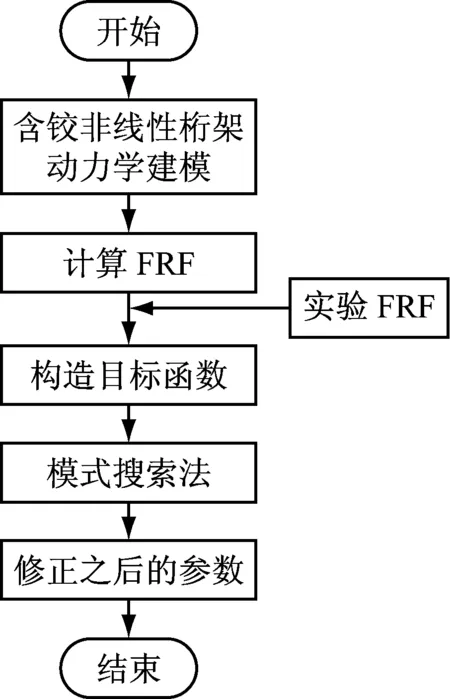
图1 基于模式搜索法的修正流程

3 描述函数法与铰链非线性特性

非线性系统的计算理论方法研究中，对于多自由度问题还有待进一步发展，目前比较常见的方法有：谐波平衡法、等效线性化法、直接积分法、相平面法、摄动法等等，这些方法有各自的特点和使用范围，对于具体问题需要选择合适的方法才能获得理想的效果。含有铰链的桁架结构属于局部非线性系统，铰链的非线性特性有固定的模型，采用谐波平衡法研究局部非线性系统在周期激励下的稳态响应，可以对系统的响应和铰链的非线性恢复力进行谐波分解，从而将问题转化为一组非线性代数方程组，采用数值方法求解，即可得到系统的非线性动力学响应。

对于弱非线性系统，可以利用谐波平衡法[20]分析受迫振动。设非线性系统受到频率为ω的任意周期力F(t)的激励，动力学方程为

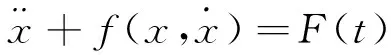
(4)

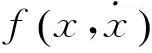
(5)

其中

(6)

代入动力学方程(4)，化为

(7)

(8)

将式(8)代入式(7)，利用三角函数公式将方程左边化作各阶谐波的线性组合，令左右两边各阶谐波的系数相等，可推导出各阶谐波的振幅an(n=1,2,…)与频率ω之间的对应关系。当级数收敛时，谐波频率愈高，振幅愈小。因此，实际计算时，可近似地取有限项代替无穷级数。对于非线性系统也可以做出与线性系统类似的频谱图，用于分析系统对周期激励的响应状况。

铰链的非线性特性一般有间隙非线性、变刚度非线性、滞回非线性、立方非线性等几种。本文考虑铰链为立方非线性，铰链恢复力具有奇函数特性，且有硬弹簧特性，力位移关系如图2所示，非线性特性由一个参数来描述：接触刚度系数kj。

含铰结构和含单铰悬臂梁的简化模型分别如图3和图4所示，Kj为铰链接触刚度系数。

含铰结构动力学方程为

(9)

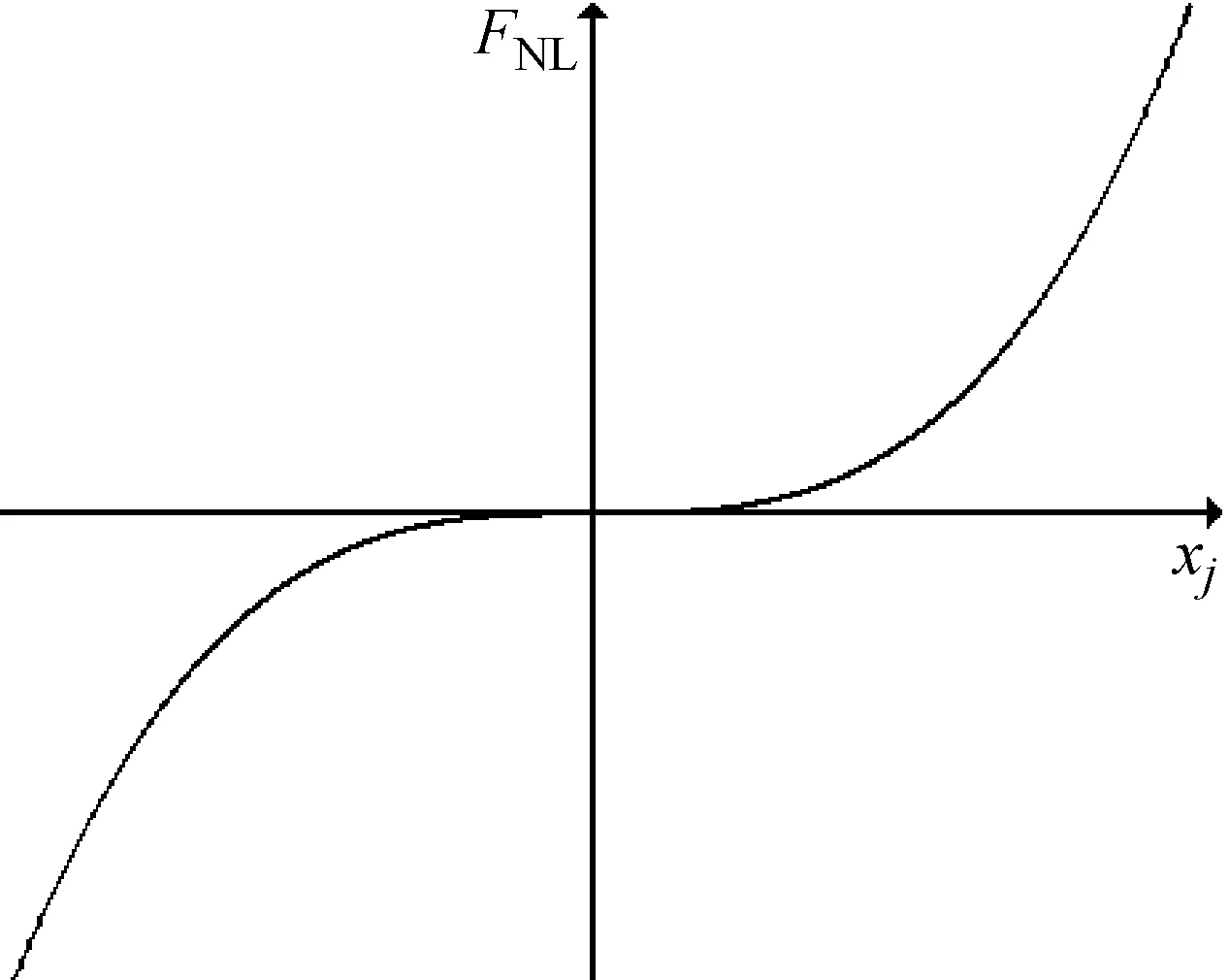
图2 立方非线性力位移关系：FNL=Kj·x3

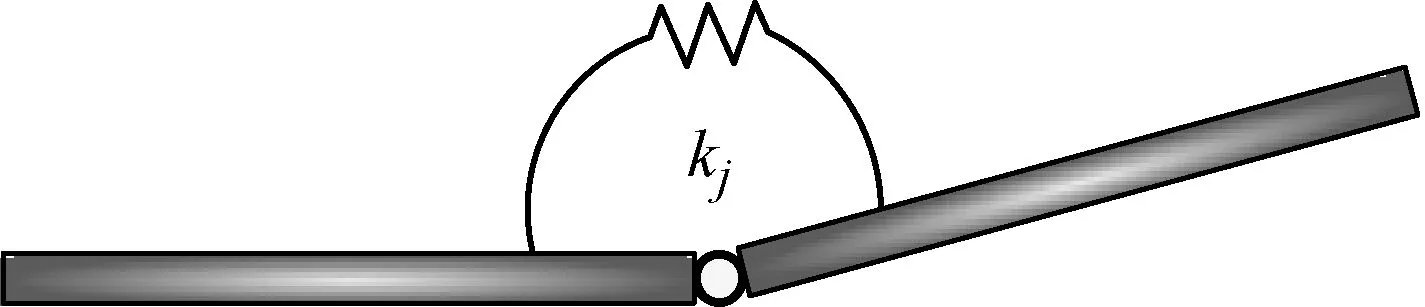
图3 含铰结构模型

图4 含单铰悬臂梁

式中:M为质量矩阵;X为节点位移向量;C为阻尼矩阵;C=αM+βK;K为刚度阵;FN为铰链引入的非线性广义力向量;FE为外部激振广义力向量。

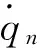
(10)

式中:an和bn为广义位移qn谐波展开中的正余弦系数。

铰链引入的非线性力可以用广义位移和速度表示为

(11)

式中：

(12)

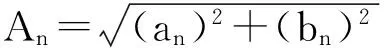
4 算例研究

4.1 含铰悬臂梁

4.1.1 频响函数计算

以图4所示的一维含铰悬臂梁为研究对象，运用1.2中的基本理论对该结构进行建模与分析计算，梁的基本参数见表1。

考虑正弦激励作用在自由端，设激振力幅值和刚度初始分别为F=0.5EI/L2，Kj=0.1EI/Le，图4中结构的频响函数变化情况如图5和图6所示。由图可知，随着激励幅值和铰链接触刚度系数的增加，结构的固有频率增大。

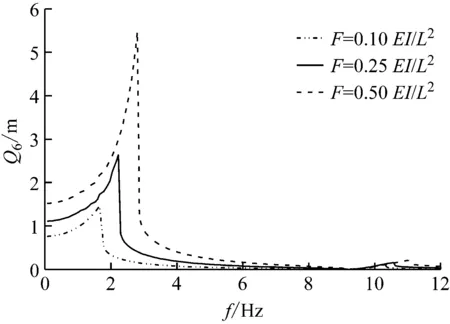
图5 激励幅值变化对频响函数的影响

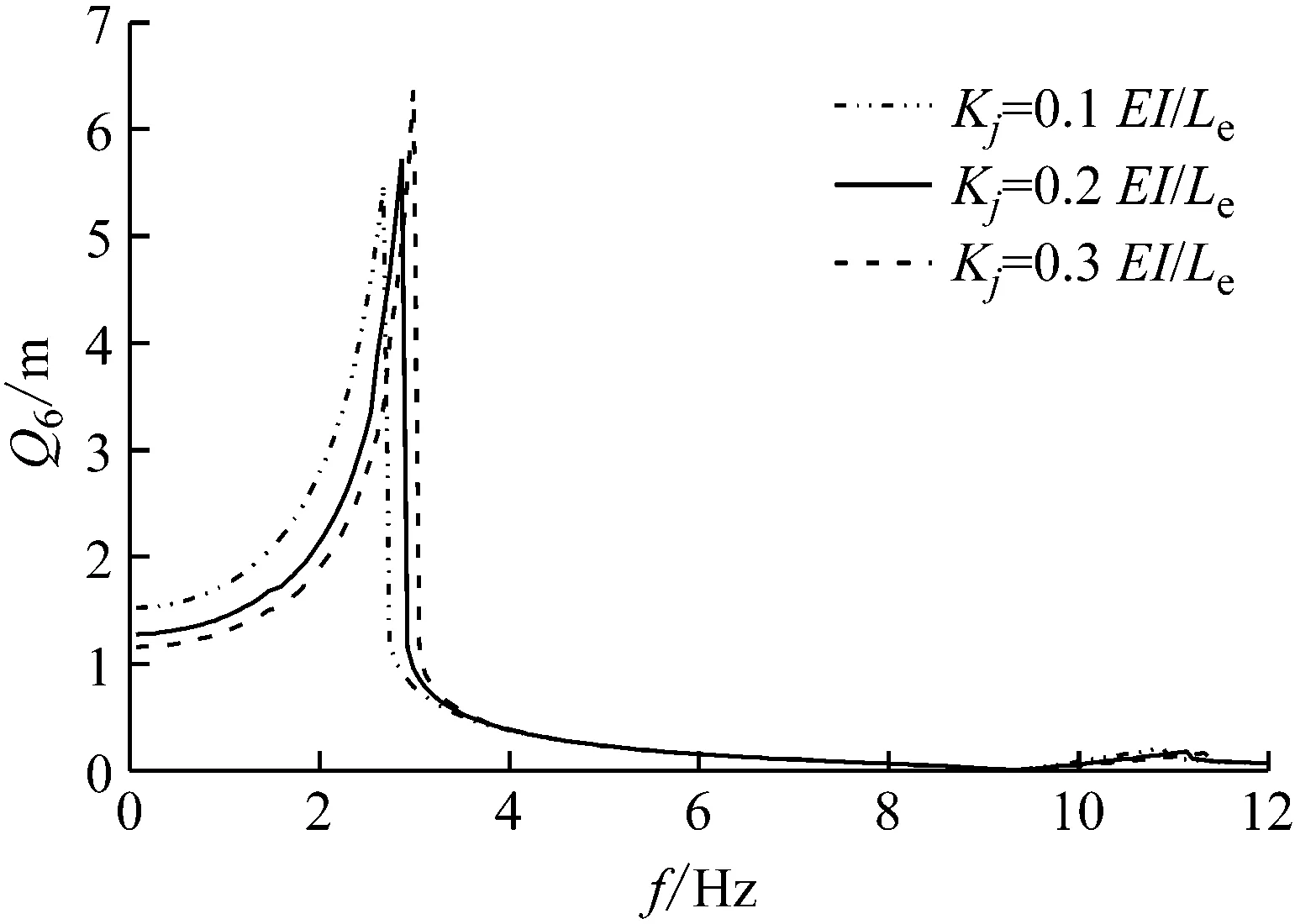
图6 铰链接触刚度系数变化对频响函数的影响

4.1.2 非线性刚度修正

设激振力幅值仍为F=0.5EI/L2，以铰链接触刚度系数Kj=0.1EI/Le作为实验值，假设模型中刚度Kj存在15%的初始误差，为0.115EI/Le。以图4中自由度6的非线性频响为特征量构造目标函数，利用模式搜索法对含铰悬臂梁结构进行模型修正，修正后值为0.1EI/Le，与实验值相吻合。图7为试验频响、初始模型频响和修正后模型频响比较结果，可见修正后的铰链接触刚度系数没有误差。

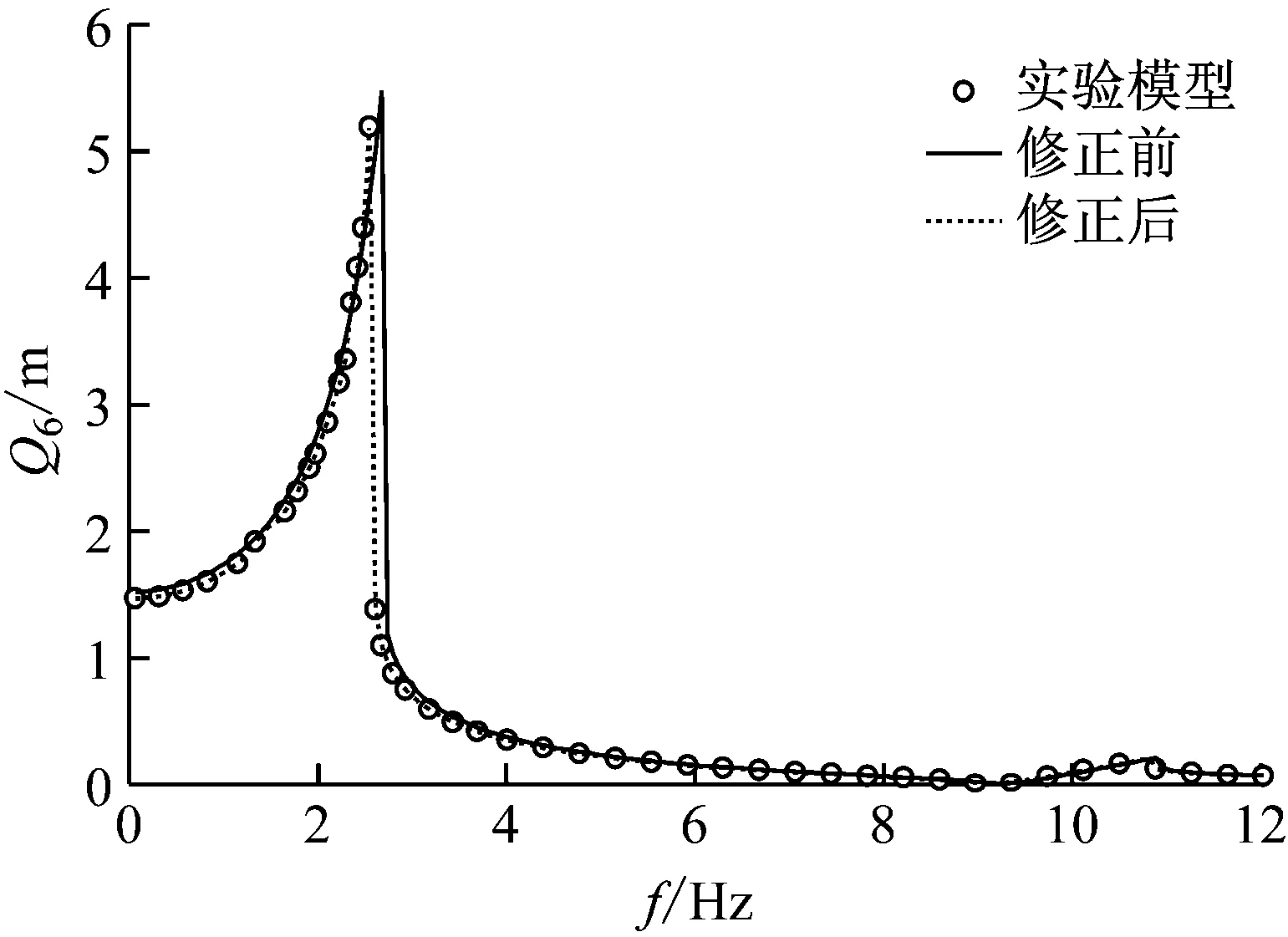
图7 15%初始参数误差修正后频响函数比较

4.2 平面桁架

4.2.1 频响函数计算

单跨平面桁架结构示意图和动力学模型，如图8和9所示。

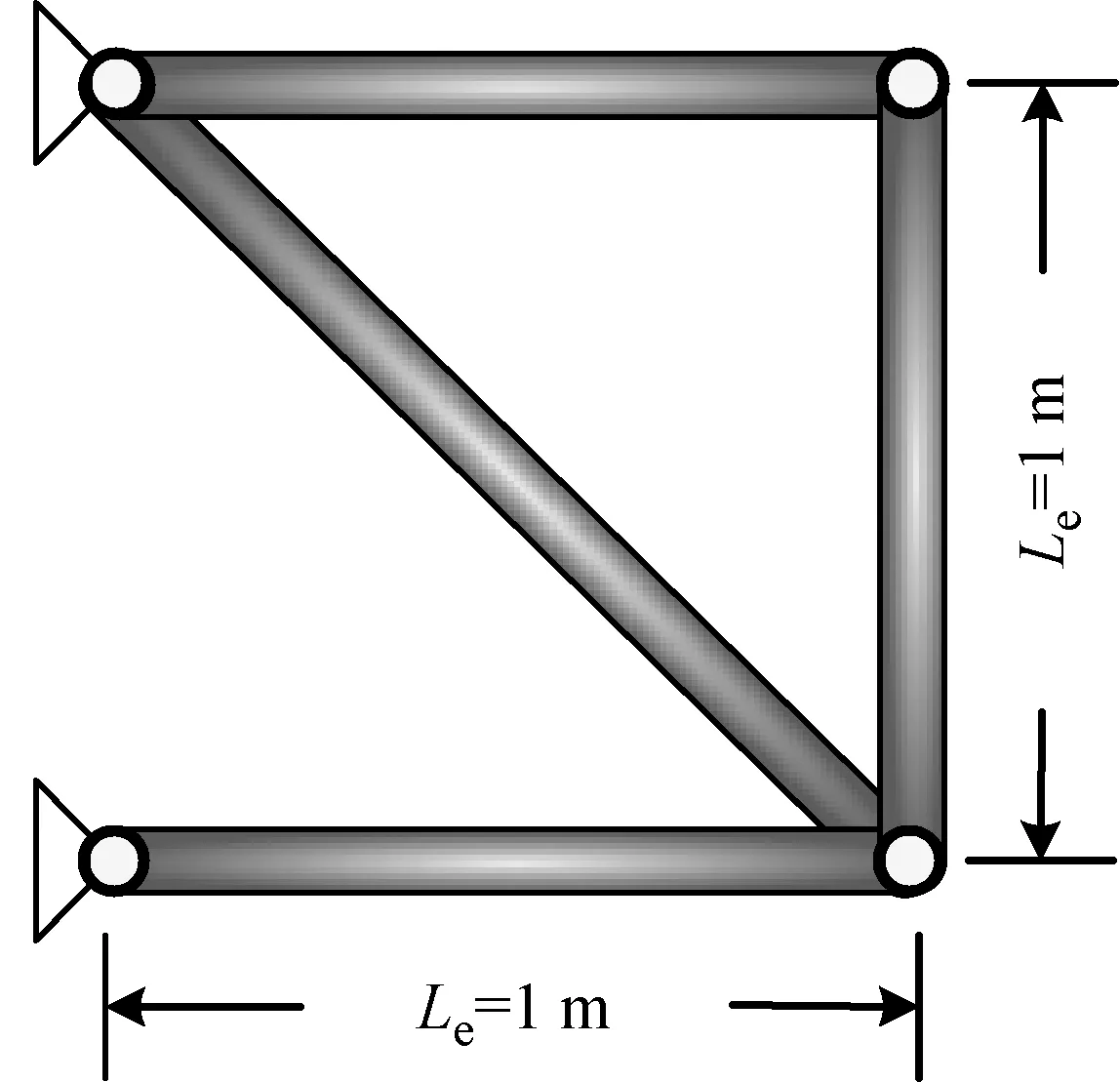
图8 单跨平面桁架结构示意图

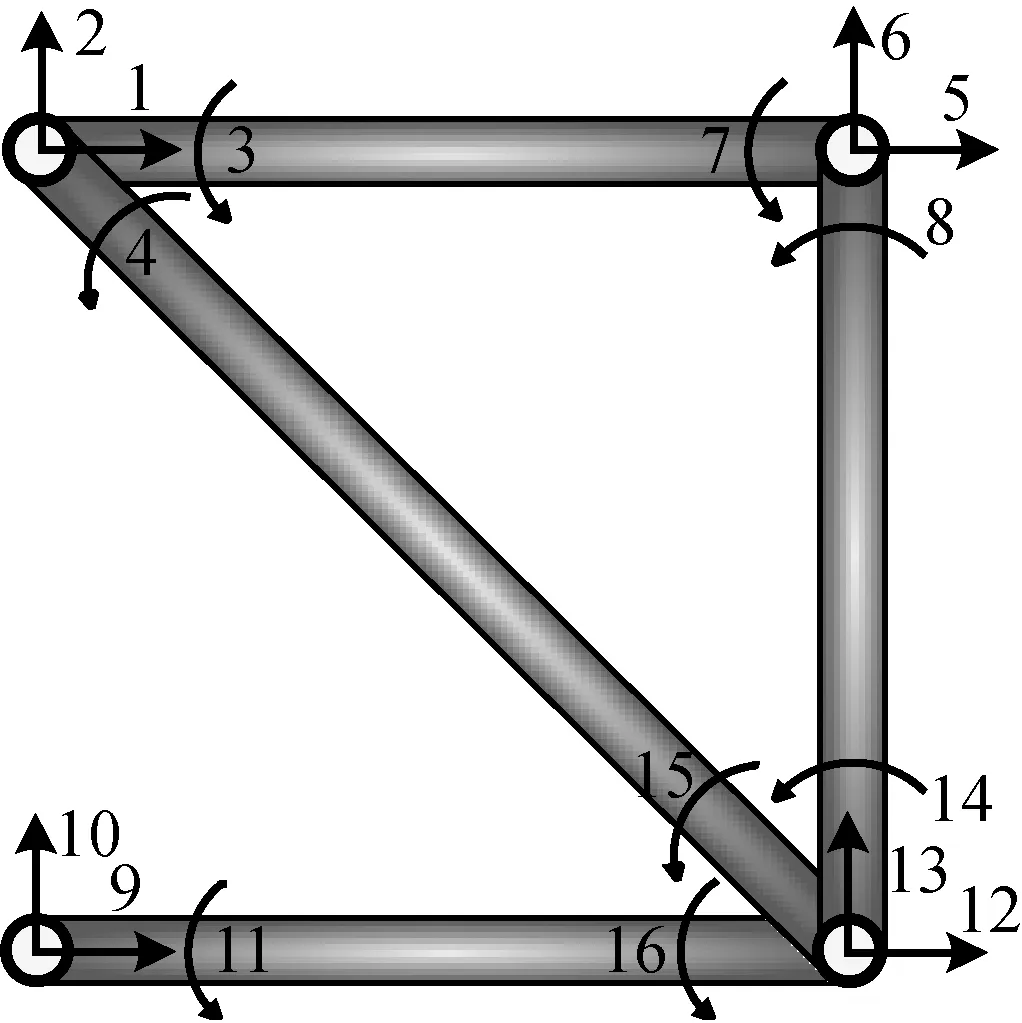
图9 单跨平面桁架动力学模型

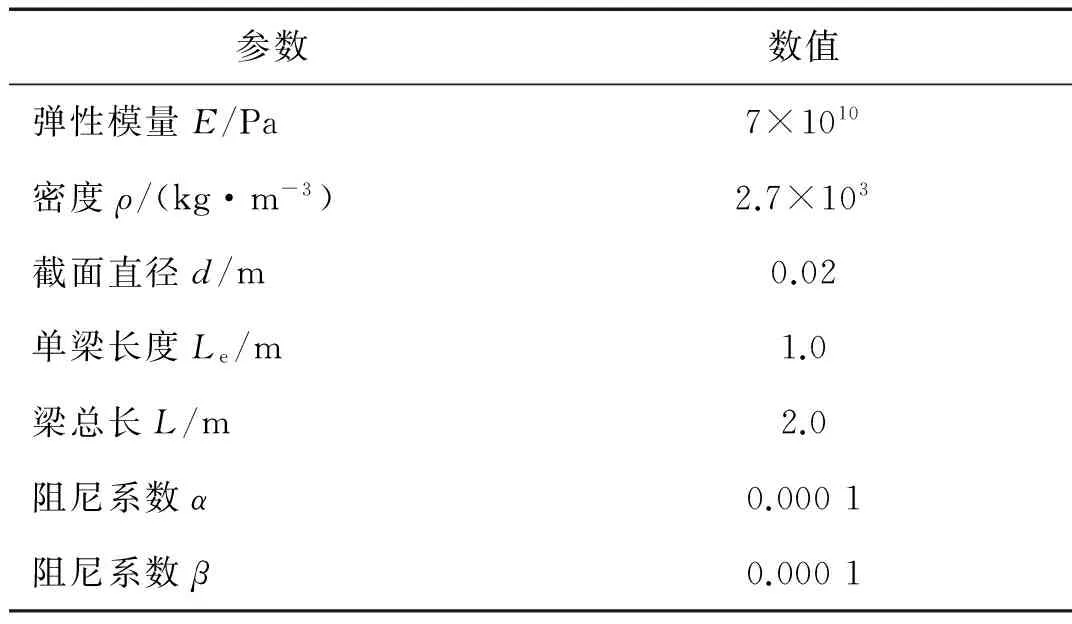
表1 梁结构的参数表

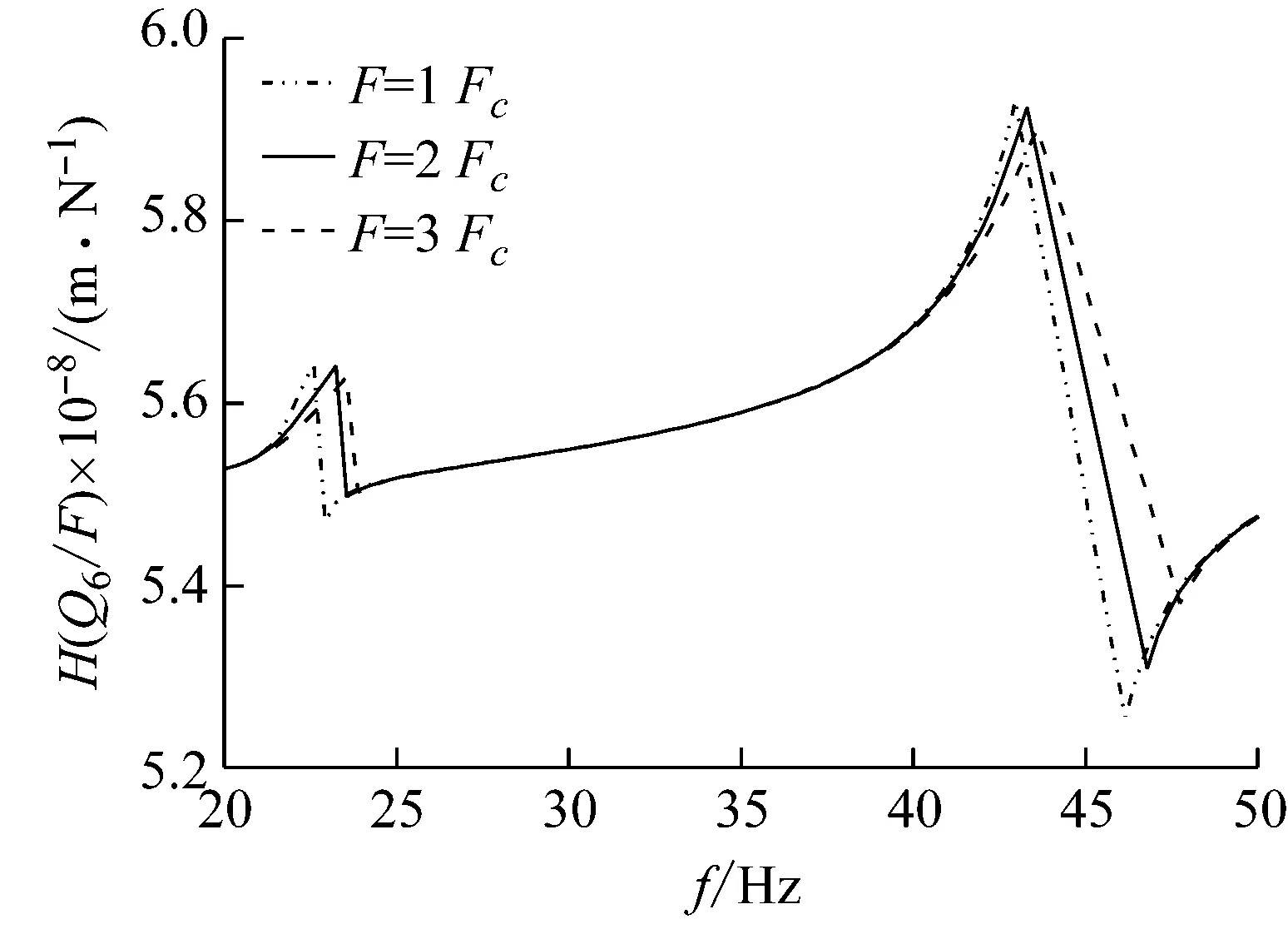
图10 激励幅值变化对频响函数影响

图11 铰链接触刚度系数变化对频响函数影响

4.2.2 非线性刚度修正

设激振力幅值仍为F=Fc，以铰链接触刚度系数Kj=0.1EI/Le作为实验值，假设模型中刚度Kj存在50%的较大初始误差，为0.15EI/Le。利用模式搜索法对含铰平面桁架结构进行模型修正，修正后值为0.1EI/Le，与实验值相吻合。图12为试验频响、初始模型频响和修正后模型频响比较，可见修正后的铰链接触刚度系数没有误差。

然而在真实实验过程中，将不可避免地存在各种噪声的干扰，为了模拟真实的实验环境并且为了检验本文提出方法的抗噪能力，对实验测得的频响函数添加不同的随机白噪声,令H(ω)=H(ω)(1+snr·μ)，SNR(Signal Noise Ratio)为信噪比，μ为-1～1的随机数[21]。利用模式搜索法进行修正，修正后值与误差如表2所示，说明该修正方法的具有一定的抗噪能力。

表2 不同噪声时修正误差对比

图12 50%初始参数误差修正后频响函数比较

一般地，桁架中的铰链接触刚度系数不完全相同，假设模型中的上面和下面两个铰链的刚度两两相同，分别为Kj1，Kj2，以考察该修正方法对多参数修正的精度。设激振力幅值仍为F=Fc，以铰链接触刚度系数Kj1=0.1EI/Le，Kj2=0.2EI/Le作为实验值，假设模型中刚度Kj1和Kj2分别存在存在+50%和-50%的较大初始误差，为0.15EI/Le和0.1EI/Le。利用模式搜索法进行模型修正，修正后值为0.1019EI/Le和0.1993EI/Le，误差为1.9%和0.7%，可见该方法对多参数修正的精度较高，图13为试验频响、初始模型频响和修正后模型频响函数的比较。

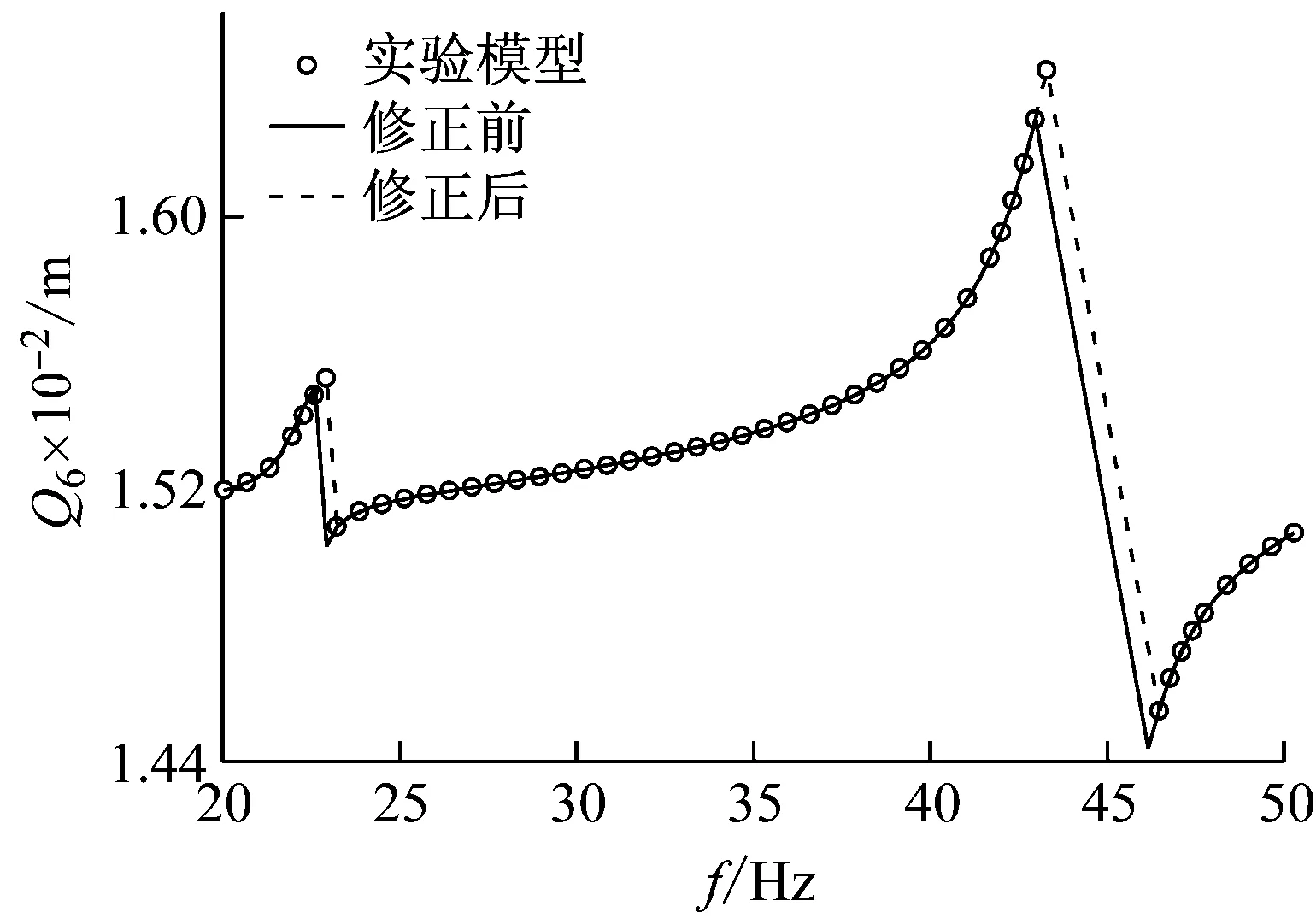
图13 多参数±50%初始误差修正后频响函数比较

5 结 论

本文提出了利用非线性频响函数对含铰非线性桁架结构进行模型参数修正的方法。

(1) 利用谐波平衡法对含铰结构进行了非线性动力学建模与响应计算，包括一维含铰梁和二维含铰平面桁架，假设铰链的非线性特性为立方非线性模型，得到了结构频响函数随着激励幅值和铰链接触刚度系数的变化规律，即固有频率分别随着激励幅值和铰链接触刚度系数的增大而增大。

(2) 采用模式搜索法对铰链的刚度进行修正，频响曲线比较结果显示，在步长和收敛准则合理的情况下，修正后结构参数误差最可达到0。铰梁结构中刚度初始假设误差较小为15%，桁架结构中刚度初始假设误差较大为50%，说明该方法是对非线性结构进行模型修正的有效方法，同时具有较高的精确性。

(3) 针对实际测试环境和结构，分别考虑试验信号加入不同的噪声和不同铰链接触刚度系数参数。该方法对引入2%噪声后的修正误差仅为2.2%，说明具有一定的抗噪声干扰能力；将铰链接触刚度系数参数调整为两个时，该方法的修正误差较小，表明方法同样适用于多参数模型修正。

[1] BROWN M A. A deployable mast for solar sails in the range of 100-1000m [J]. Advances in Space Research, 2011, 48(11):1747-1753.

[2] 赵林燕. 星载可展开天线展开过程的仿真与分析[D]. 西安: 西安电子科技大学, 2011:1- 6.

[3] 郭宏伟, 刘荣强, 邓宗全. 空间索杆铰接式伸展臂性能参数分析与设计[J]. 北京航空航天大学学报, 2008, 24(10):1186-1190.

GUO Hongwei, LIU Rongqiang, DENG Zongquan. Per-formance of parameters analysis and design of space cable-strut deployable articulated mast[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 24(10): 1186-1190.

[4] FERNEY B D, FOLKMAN S L. Results of force-state mapping tests to characterize struts using pinned joints[C]∥Proceedings of the 36th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Con-ference. 1995.

[5] FOLKMANT S L, BINGHAM J G, CROOKSTON J R. The joint damping experiment[R]. NASA,1997.

[6] TOMIHIKO Y. Dynamic characteristic formulations for jointed space structures[J]. Journal of Spacecraft and Rockets, 2006, 43(4):771-779.

[7] BOWDEN M L. Dynamics of space structures with nonlinear joints[D]. Cambridge: Massachusetts Institute of Tech-nology, 1988.

[8] WEBSTER M S. Modeling beam-like space trusses with nonlinear joints with application to control[D]. Cambridge: Massachusetts Institute of Technology. 1991.

[9] SARKAR S, VENKATRAMAN K. Dynamics of flexible structures with nonlinear joints[J]. Journal of Vibration and Acoustics, 2004, 126(1):92-100.

[10] 黄铁球, 吴德隆, 阎绍泽. 带间隙伸展机构的非线性动力学建模[J]. 中国空间科学技术, 1999, 19(1):7-13.

HUANG Tieqiu, WU Delong, YAN Shaoze. Nonlinear dynamic modeling of deployable structures with clearance[J]. Chinese Space Science and Technology, 1999, 19(1): 7-13.

[11] 陈鹿民, 阎绍泽，金德闻，等. 含间隙铰空间可展桁架结构的动力学实验研究[J].清华大学学报, 2003, 43(8): 1027-1030.

CHEN Lumin, YAN Shaoze, JIN Dewen, et al. Dynamics experiment of a space deployable truss structure with joint clearance[J]. Journal of Tsinghua University, 2003, 43(8): 1027-1030.

[12] 尉立肖, 刘才山. 圆柱铰间隙运动学分析及动力学仿真[J]. 北京大学学报, 2005, 41(5): 679-687.

WEI Lixiao, LIU Caishan. Kinematic analysis and dynamics simulation of cylinder joint clearance[J]. Journal of Peking University, 2005, 41(5): 679-687.

[13] 阎绍泽, 叶青, 申永胜, 等. 间隙对空间可展结构动力学性能的影响[J]. 导弹与航天运载技术, 2002(6): 42-46.

YAN Shaoze, YE Qing, SHEN Yongsheng, et al. Effects of clearances on dynamic performances of deployable structures for spacecraft[J]. Missiles and Space Vehicles, 2002(6): 42-46.

[14] JIANG Dong，ZHANG Peng，FEI Qingguo，et al. Comparative study of model updating methods using frequency response function data[J]. Journal of Vibroengineering, 2014, 16(5): 2305-2318.

[15] 费庆国, 李爱群, 张令弥. 基于神经网络的非线性结构有限元模型修正研究[J]. 宇航学报, 2005, 26(3):267-269.

FEI Qingguo, LI Aiqun, ZHANG Lingmi. Research on updating of finite element model of nonlinear structures based on neural network[J]. Journal of Astronautics, 2005, 26(3):267-269.

[16] TANG Jiashi, HUO Quangzhong. Identifying parameters of nonlinear system in time domain by the response of free vibration[J]. Journal of Vibration Engineering,1989,2:1-6.

[17] PENG Jiehua. Frequency method of parameter identification of nonlinear systems[J]. Journal of Shaoyang University,2004(3):3-10.

[18] YASUDA K. Identification of nonlinear multi-degree-of-freedom systems[J]. JSME International Journal,1988,31(1):1-8.

[19] 马睿, 姜东, 费庆国, 等. 考虑重力影响的太阳翼模型修正方法研究[J]. 宇航学报, 2014, 35(12): 1373-1378.

MA Rui, JIANG Dong, FEI Qingguo, et al. A model updating method for solar array considering the influence of gravity[J]. Journal of Astronautics, 2014, 35(12): 1373-1378.

[20] 刘延柱,陈立群,陈文良.振动力学[M]. 北京: 高等教育出版社, 2011.

[21] 李伟明, 洪嘉振. 基于频响函数的模型修正方法[J]. 上海交通大学学报, 2011, 45(10): 1455-1459.

LI Weiming, HONG Jiazhen. Research on model updating method based on frequency response functions[J]. Journal of Shanghai Jiaotong University, 2011, 45(10): 1455-1459.