框架结构采用调频液柱阻尼器的设计方法研究

符 川

(北方工业大学 土木工程学院，北京 100144)

调频液柱阻尼器(Tuned Liquid Column Damper, TLCD)由U型管及管内液体(或水)构成，U型液体长度(即水平管长度与垂直管水面高度)可以改变管内液体的自振周期，当自振周期达到调谐周期及阻尼比达到最佳阻尼比时，对建筑物具有最佳减振效果。Hochrainer[1]将TLCD用于抑制高层建筑结构在单向动力作用下的水平振动。Diana[2]考虑阻尼器的非线性效应，采用Hardware-in-the-Loop试验模拟TLCD在铁塔对风荷载作用下的减振性能。霍林生等[3]研究了半主动变刚度TLCD的减振性能。钟振宇等[4]研究了非等截面TLCD在高层建筑上对脉动风荷载减振的有效性。TLCD由于具有经济、简单易行、维护费用少和减振效果好的特点在高层建筑的风振控制中得到了较为广泛的应用，如日本Hyatt酒店、Ichida大厦、Milennium塔等。

为了使吸能减振装置振动控制效果达到最好，设置的最佳位置和最优参数是阻尼结构设计中的重要环节。对于平面对称结构采用剪切型模型，阻尼器应尽量布置在结构位移最大的层才能充分发挥其耗能能力。然而目前结构阻尼器在非对称结构中优化设置的研究很少。李宏男等[5]利用改进的遗传算法中二进制单点交叉，对多层结构在二维地震作用下作动器布置准则进行分析，该方法比穷举法快速有效。吴学淑[6]以单层非对称结构作为平面非对称多高层建筑结构的简化模型，研究速度型阻尼器在平面的最优偏心位置。传统的阻尼器参数优化设计方法主要是利用随机振动理论和现代控制理论，以主体结构位移均方根和加速度均方根最小作为优化目标[7-8]。张琴等[9]采用等效刚度和等效阻尼力学模型，基于LQR控制优化理论提出了黏弹性阻尼器参数优化方法，将被动控制效果与主动控制效果逼近，通过矩阵初等变换，根据最小二乘法推导了参数优化公式。李祥秀等[10]从功率的角度分析了TMD系统在地震激励下减振效果，以主结构的耗能功率最小为优化目标得到TMD最优频率比及阻尼比。

本文给出TLCD控制结构地震响应的运动方程，采用模态速度瞬心法确定阻尼器在非对称结构楼面最佳位置，并用遗传算法二次优化。同时研究TLCD的几何尺寸(质量比、倾斜角、长度比)和参数优化的设计方法，给出了阻尼器的设计流程，并按此设计方法对30层偏心结构进行了减振控制分析。

1 调谐液柱阻尼器运动方程

1.1 水平向TLCD运动方程

平面对称、多层框架结构质量中心与刚度中心重合且在一条直线上时，通常将此结构简化成层间剪切、平面模型，分别在其两个主轴方向进行抗震计算。假设在此结构第i层放置一调谐液柱阻尼器，用以控制结构某个主轴方向的位移，阻尼器管道中的理想液体运动方程可由广义Bernoulli方程建立[11]

(1)

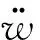
它对结构的控制力可表示为

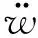
(2)

式中：mf为阻尼器中液体质量，Fx为水平控制力。

1.2 偏心TLCD运动方程

平面非对称、多层框架结构质量中心与刚度中心不重合，其基本力学模型采用空间杆系-层间模型，考虑刚性楼板假定，即楼面拥有3个自由度，两个水平分量和一绕竖轴的转动分量。霍林生等[12]提出在结构两主轴方向垂直设置TLCD用来减小地震作用下结构的平移-扭转耦联反应，本文给出了倾斜放置的TLCD运动方程。

假设在结构第i层偏心放置一调频液柱阻尼器，其水平管段中心Ai(xAi,yAi,0)并与x方向成γ角，在刚性管道系统中理想液体的运动方程由广义Bernoulli方程建立

(3)

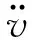
TLCD与建筑结构在振动过程中发生的相互作用力和力矩利用动量和角动量守恒得出

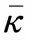
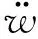
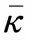
作用在Ai点的控制力将对质量中心产生扭转力矩

MCMiz=MAiz-FAix(yAi-yCMi)+FAiy(zAi-zCMi),

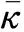
(4)

2 TLCD位置优化

一般剪切型建筑结构在地震作用下，结构地震反应常以第一振型分量为主，即结构相对于地面最大位移反应发生在结构的顶层，因而可将TLCD系统安装在结构的顶层控制第一振型，这样对结构地震反应的控制效果显著。如控制多个振型阻尼器应尽量布置在结构位移最大的层。

对于复杂结构采用穷举法确定TLCD的设置位置仅适合结构层数较少的情况，随着层数的增加, 穷举法的计算量将以指数形式增长, 计算时间长，在实际工程中难以应用。本文根据振型模态速度瞬心确定阻尼器位置，再根据工程实际情况采用遗传算法控制某个设计目标得到阻尼器的最优位置。

2.1 模态速度瞬心

结构的质量中心CM、刚度中心CS与几何中心O都不重合。第i层楼面质心坐标为(xCMi,yCMi)，rSi回转半径。任意振型的水平位移和扭转可以转化成以模态速度瞬心为基点的扭转。位于第i层楼面j振型的模态速度瞬心表示为

φj(3i-1)，

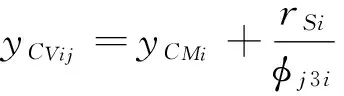
(5)

当模态速度瞬心位于楼面外，偏心放置U/V型调频液柱阻尼器能有效控制以水平为主的耦联反应，其最佳位置为使其到模态速度瞬心的垂直距离最大[13]。

2.2 遗传算法

利用多个TLCD控制结构相应振型需采用遗传算法将TLCD位置二次优化，即运用MATLAB自带的遗传算法与直接搜索工具箱(Genetic Algorithm and Direct Search Toolbox)编制遗传优化程序。结构布置阻尼器的目的是要控制结构的振动响应，优化阻尼器位置的目的就是在相同阻尼器参数的前提下使结构振动响应最小。每个阻尼器位置有3个变量，阻尼器中心Ai(xAi,yAi)和与x轴的夹角为γi，以楼面尺寸为矩形a×b为例，约束条件为

(6)

3 TLCD几何尺寸优化

根据动力吸振理论，TLCD管道的液柱质量必须大于主结构质量或欲控模态对应的广义质量的1%[13]。质量比越大，结构的等效阻尼比也越大，但随着质量比的增加，等效阻尼比的增加幅值减小。且质量比过大会造成结构重量加大，恒载提高，加大结构的静力反应，故TLCD质量比需小于6%[14]。

β为竖向管道与水平管道的夹角，β为锐角时竖向管道向外, 钝角时竖向管道向内。由式(2)和(4)可得，β为锐角时水平控制力达到最大。同时为了满足液体最大相对速度控制在10 m/s以下以保证液体气体接触面水平[15]，β宜取π/4<β≤π/2。当两段竖向管道为非均匀截面，式(1)和(3)非常复杂并且具有高度非线性，因此，具有均匀截面的竖向管道是最佳选择。

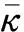
4 TLCD参数设计

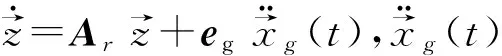
(5)

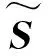
图1 TLCD-框架结构体系与TMD-框架结构体系

Fig.1 TLCD-shear frame and TMD-shear frame (plan-symmetric structure using shear model,SDOF host structure)

4 TLCD设计流程

调频液柱阻尼器的设计流程：①选定调频液柱阻尼器内液体质量与管道截面面积、管长，并算出与主结构的质量比；②计算等效调谐质量阻尼器与主结构质量比；③根据质量比计算调谐频率比和最佳阻尼比；④计算阻尼器自然频率及等效线性阻尼常数；⑤设计阻尼器管道的管壁厚度、重量等(如表1)。

5 数值计算

本文选用30层的平面非对称框架结构，楼层质量为384 000 kg。楼板对质心转动惯量为5.96×106kg·m2，x轴方向和y轴方向都得层间剪切刚度分别为kx=8.64×108N/m，ky=7.8×108N/m。层间扭转刚度kt=1.38×1011N·m/rad。结构x方向的偏心距ex=4 m，y方向的偏心距ey=3 m。结构前三个频率为0.348、0.384和1.042 Hz[12]。根据前3个模态瞬心的位置Cv，在顶层放置2个TLCD和10层1个TLCD来控制结构前三阶振型，如图2所示，CM为质量中心、CS为刚度中心。TLCD中水的质量为270×103kg，250×103kg和50×103kg，几何尺寸和优化参数见表2。

表1 调谐液柱阻尼器的设计流程(平面对称框架结构，多自由度)

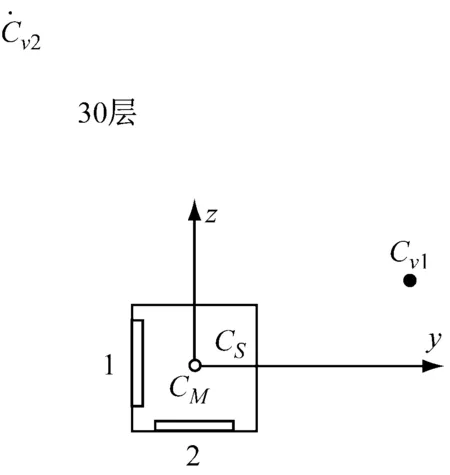
图2 TLCD安装位置

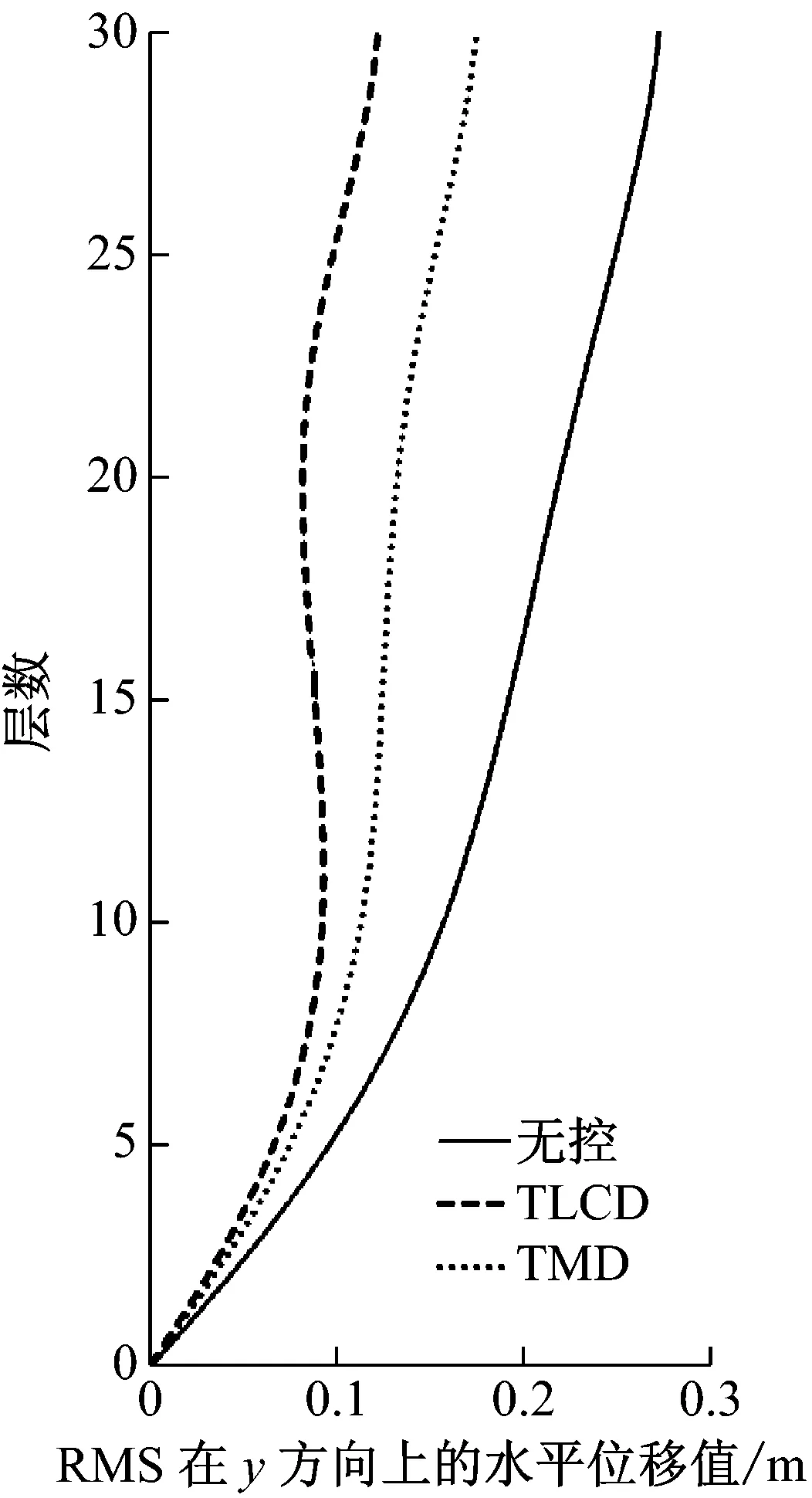
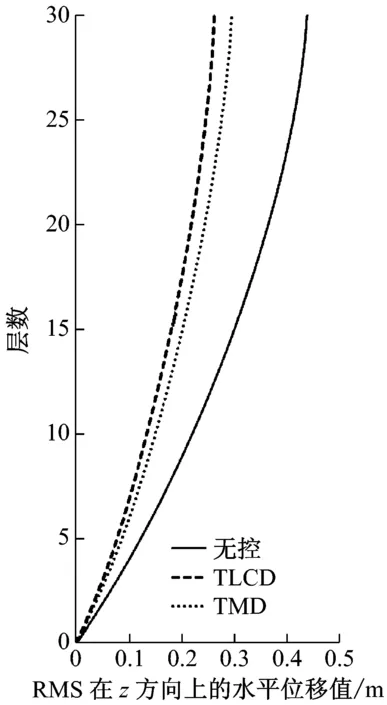
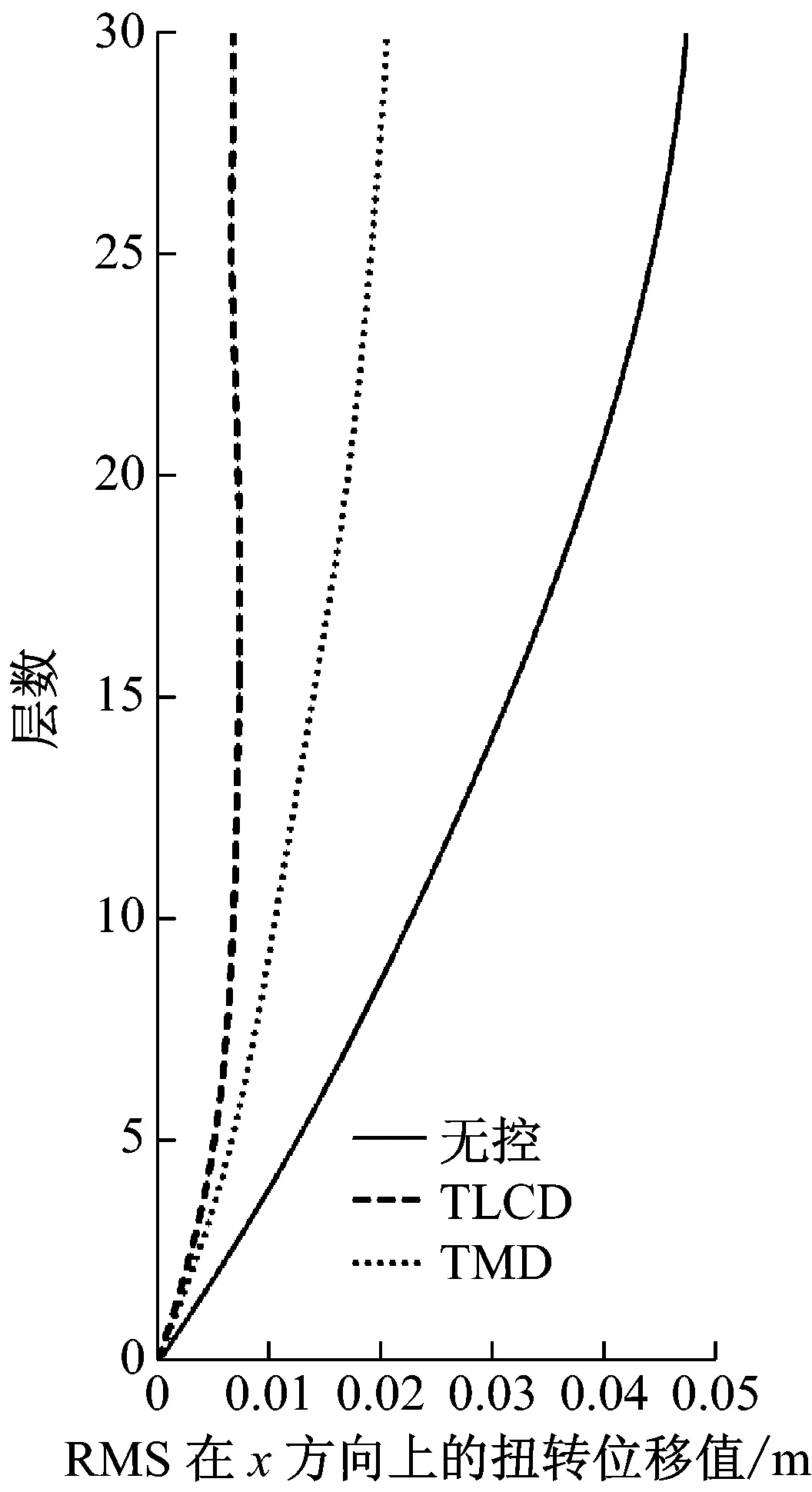
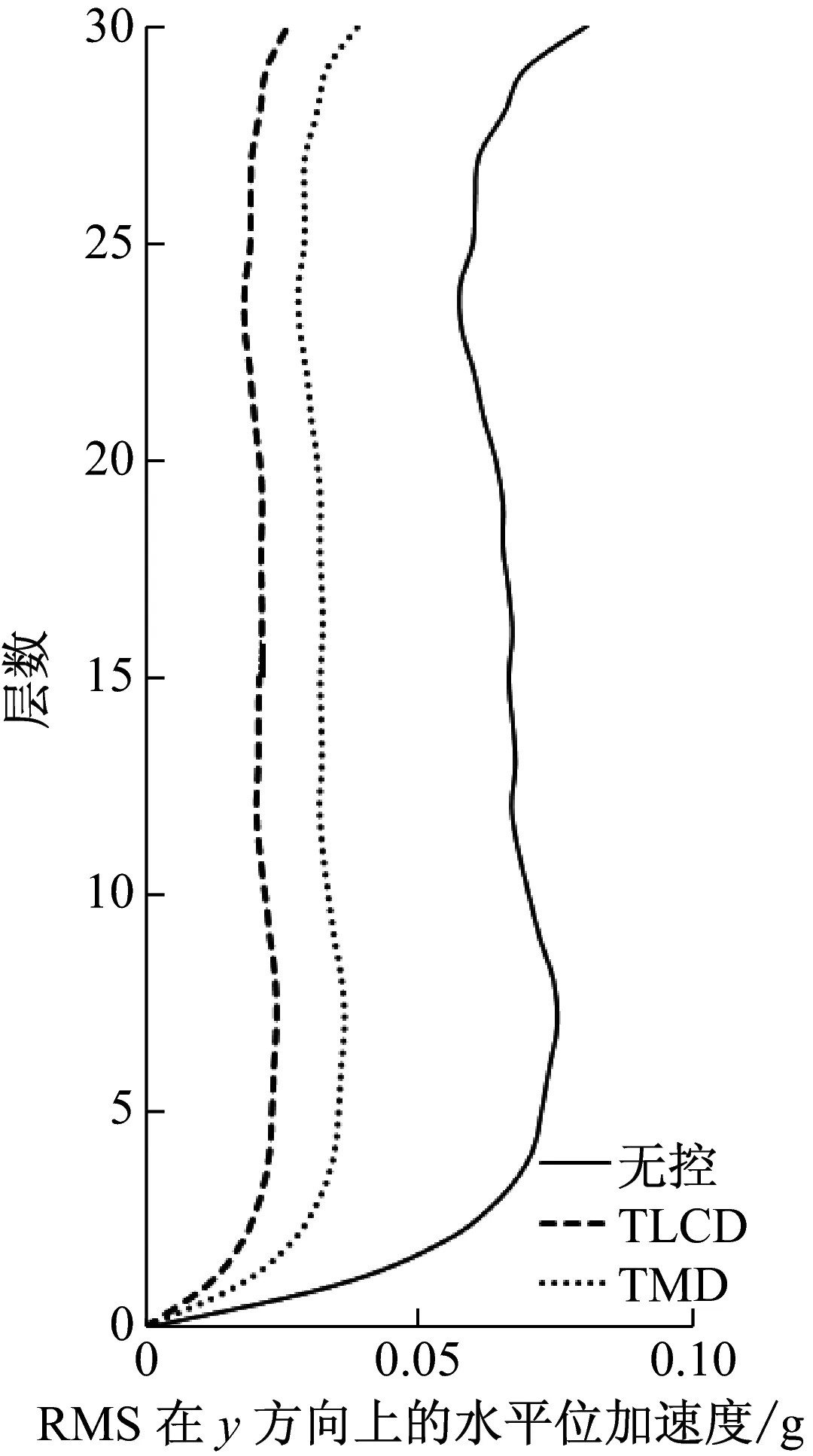
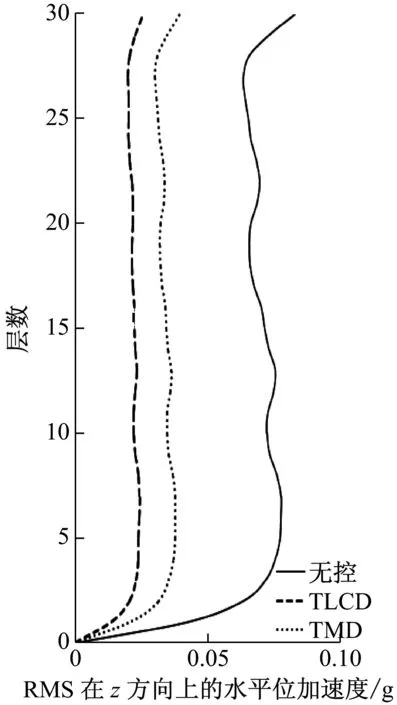
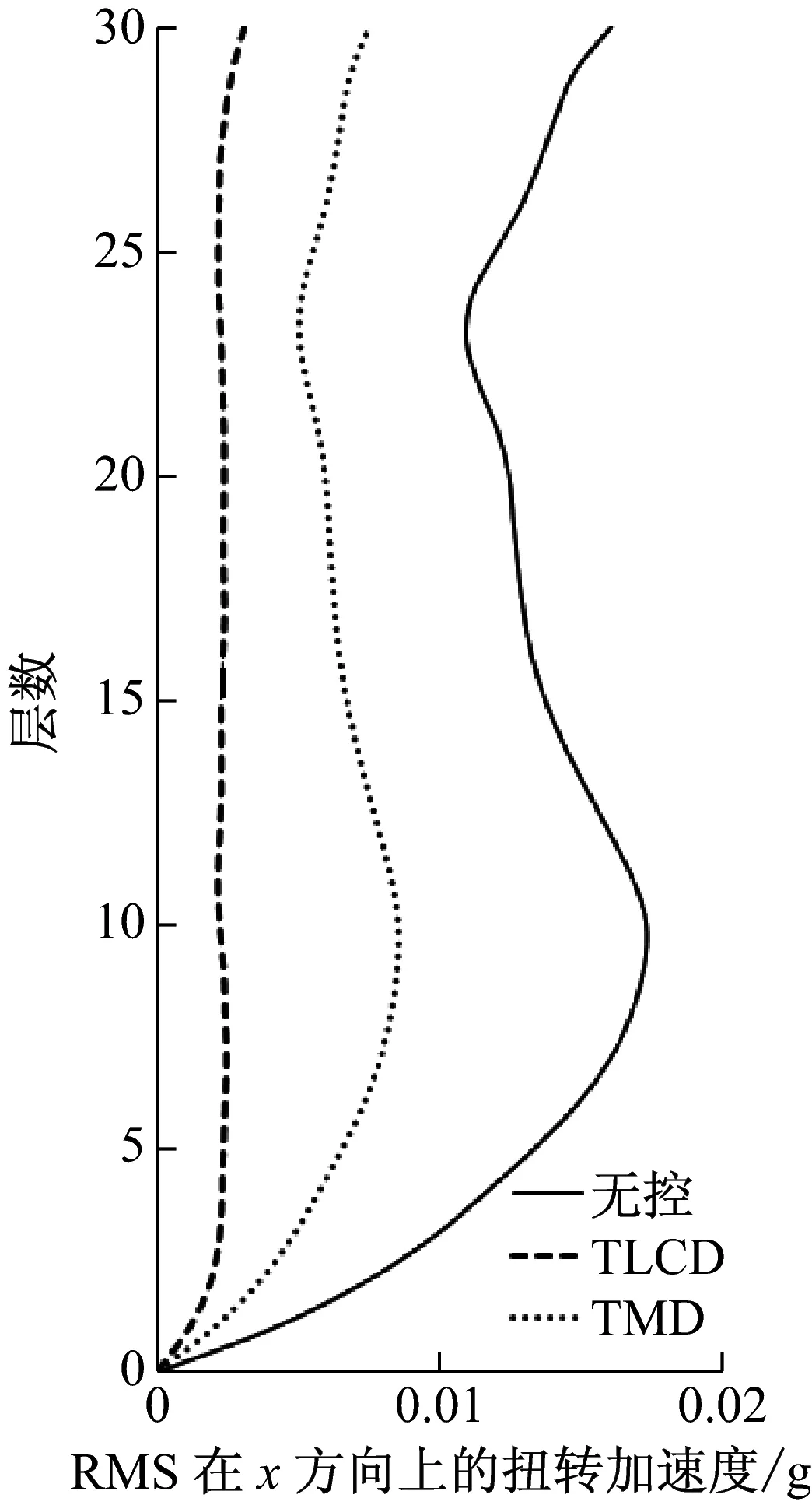
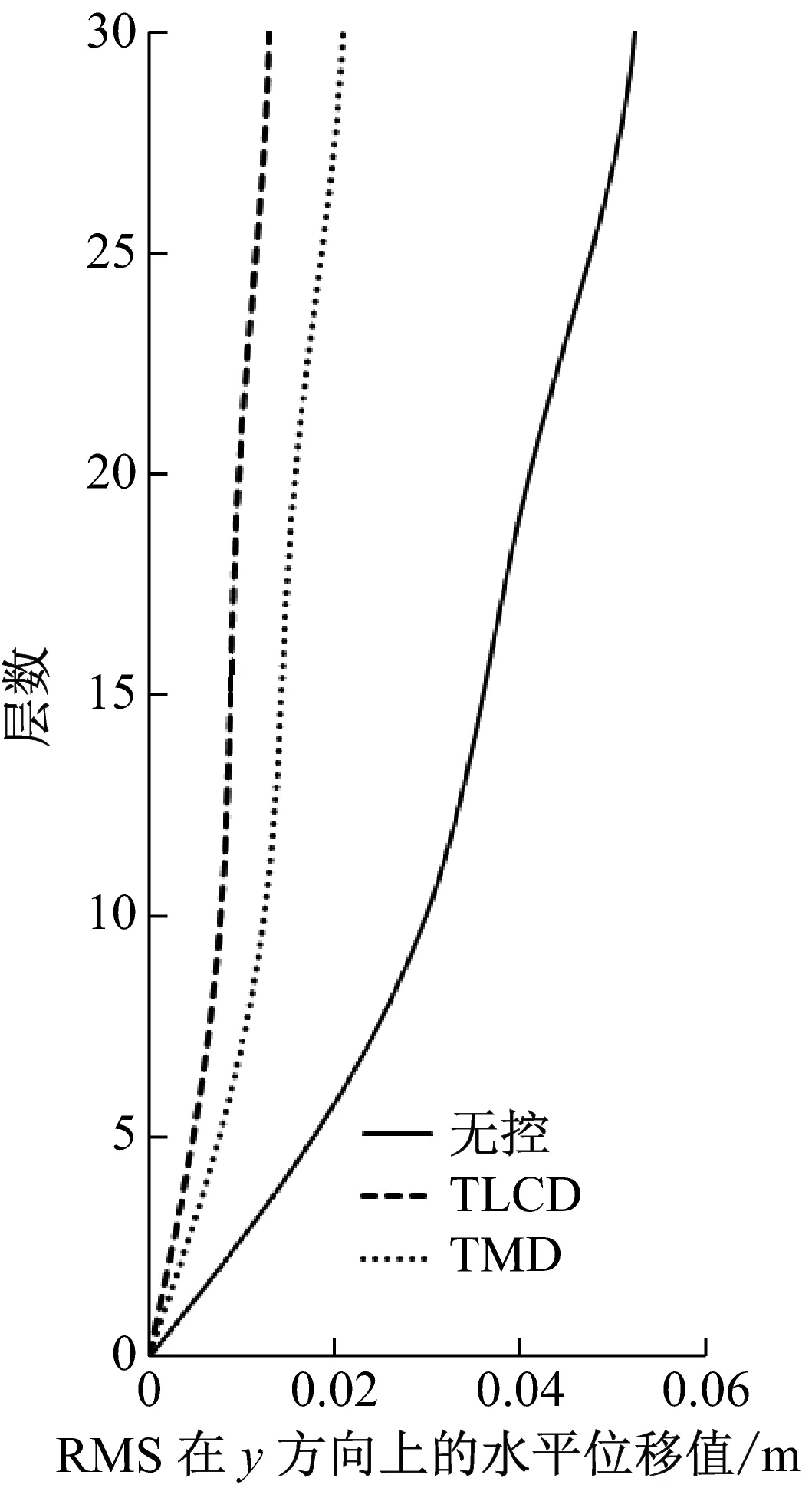
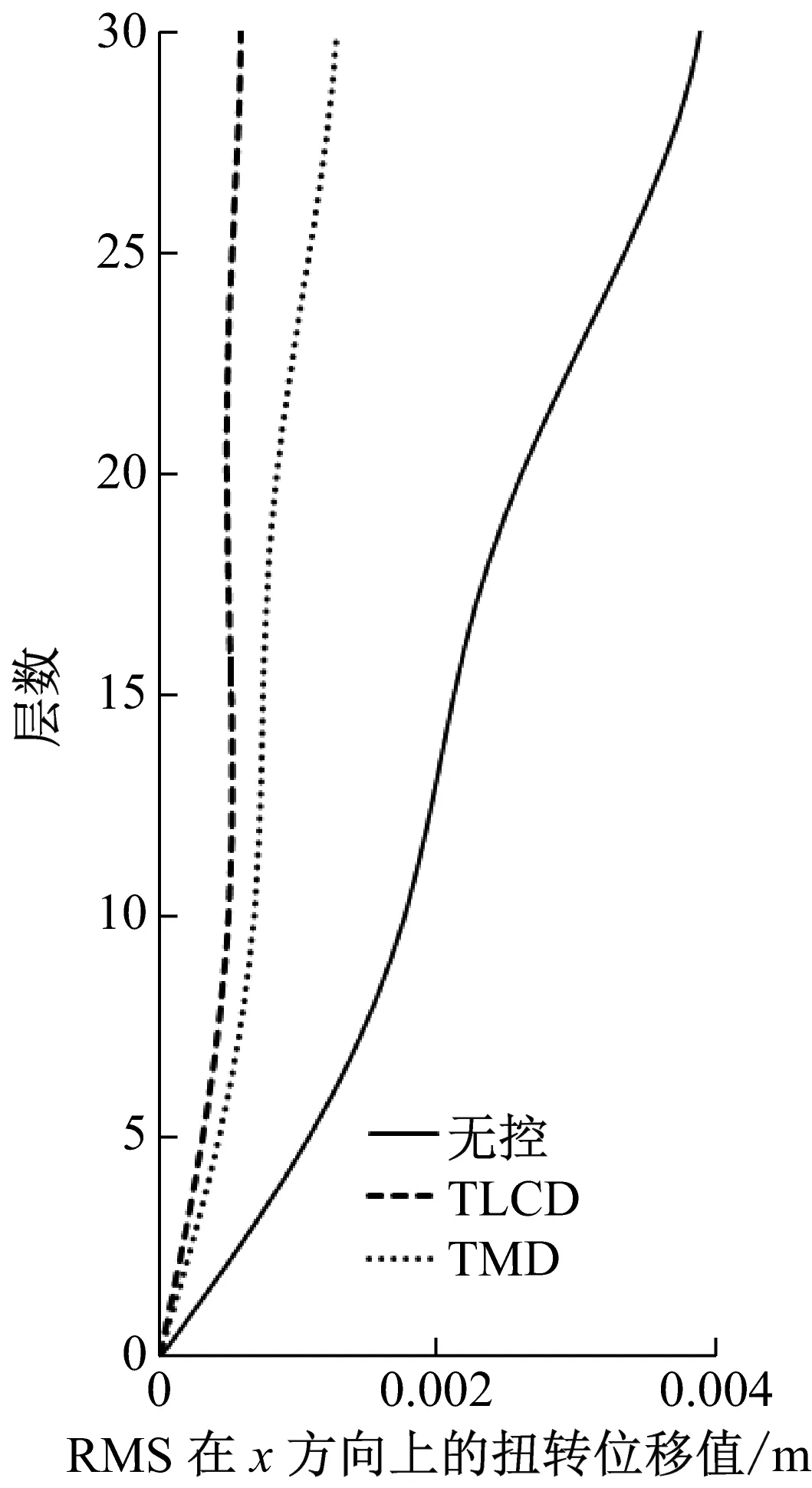
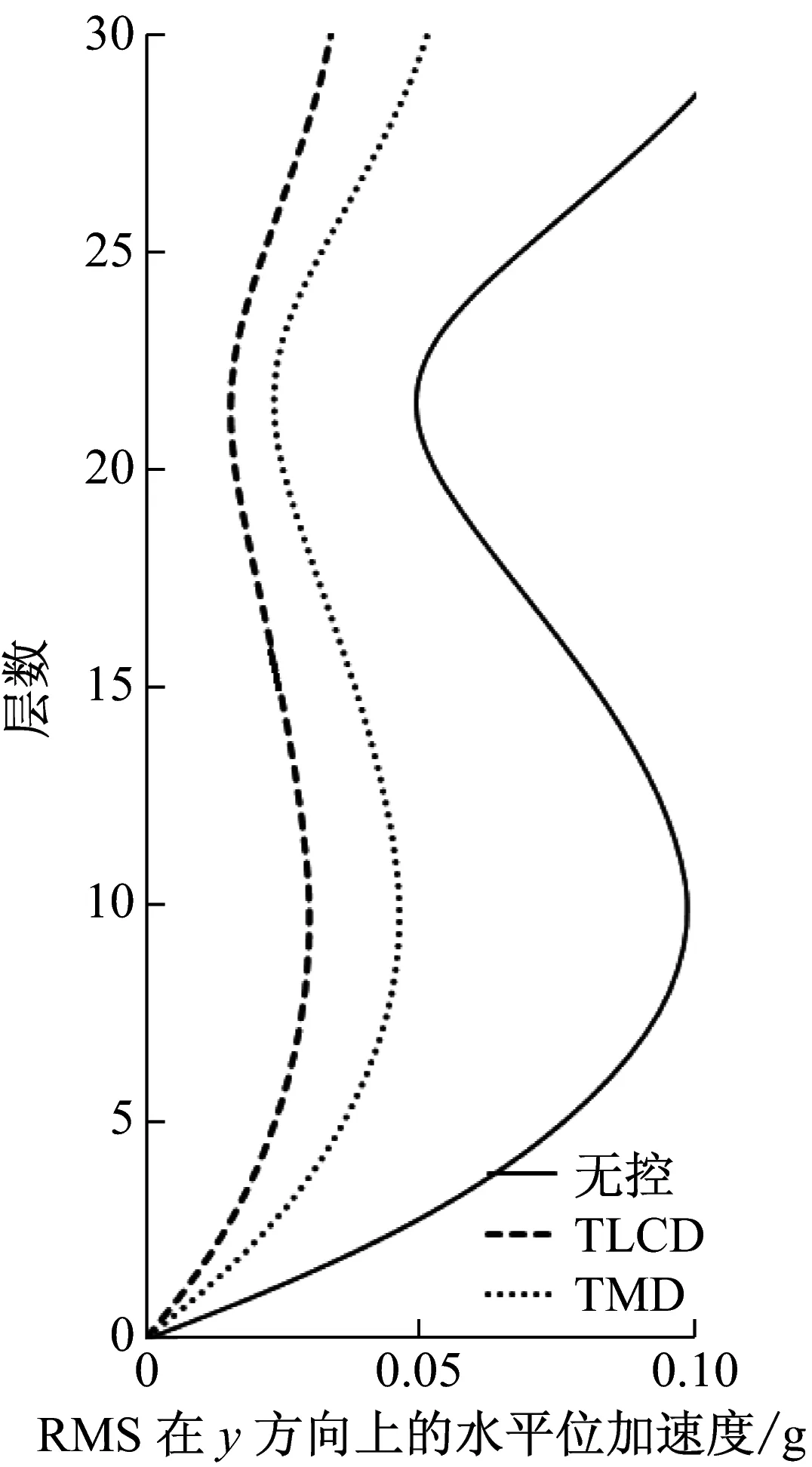
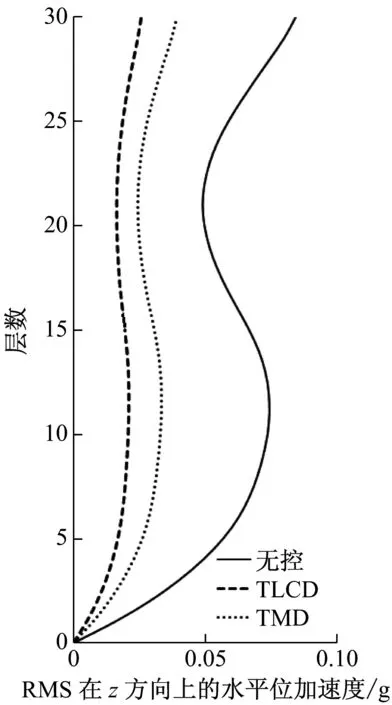
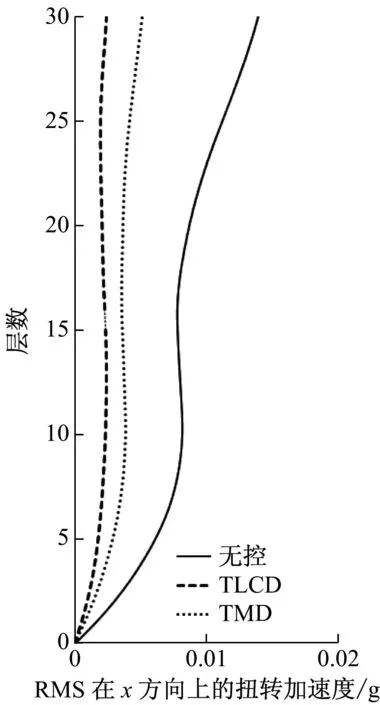
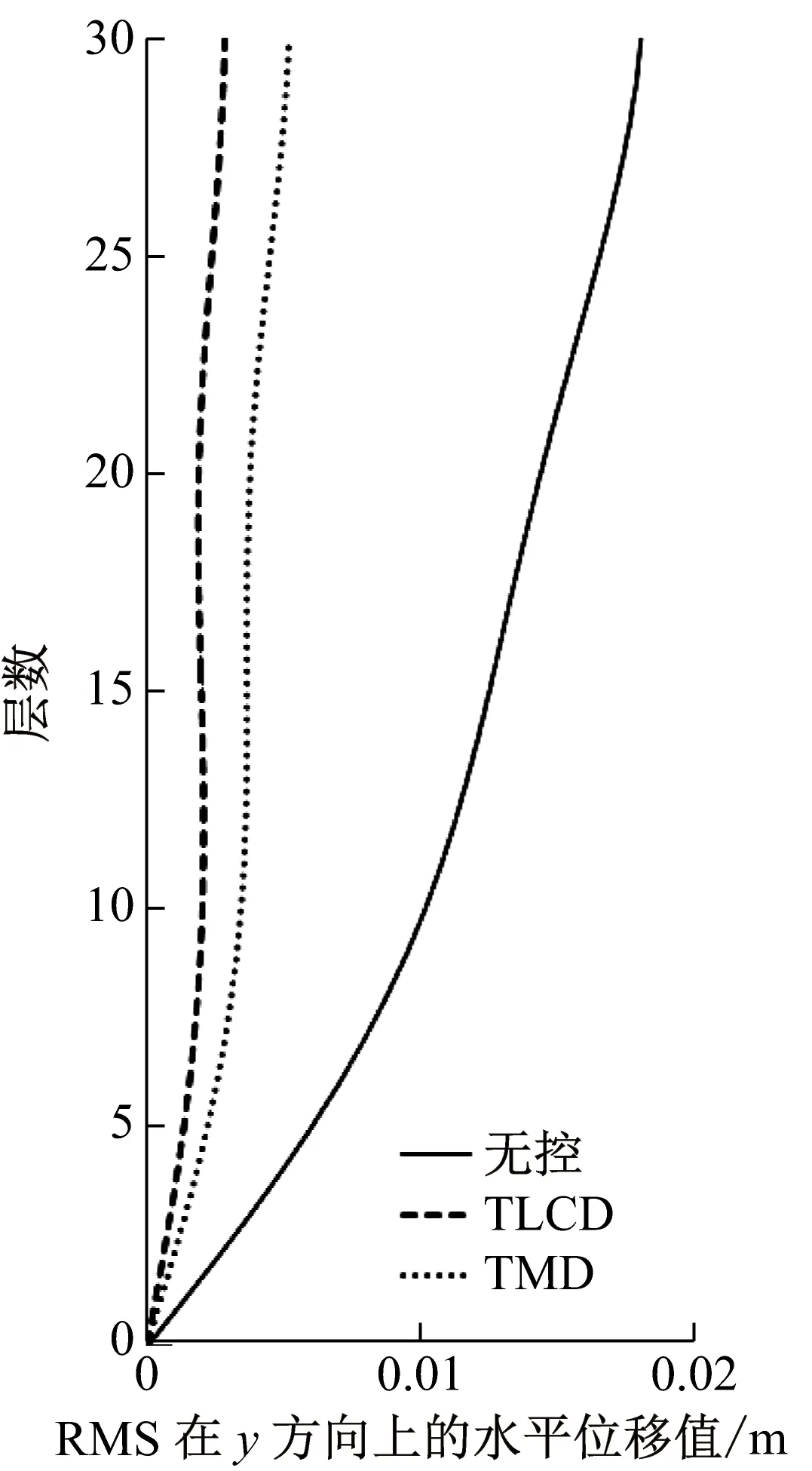
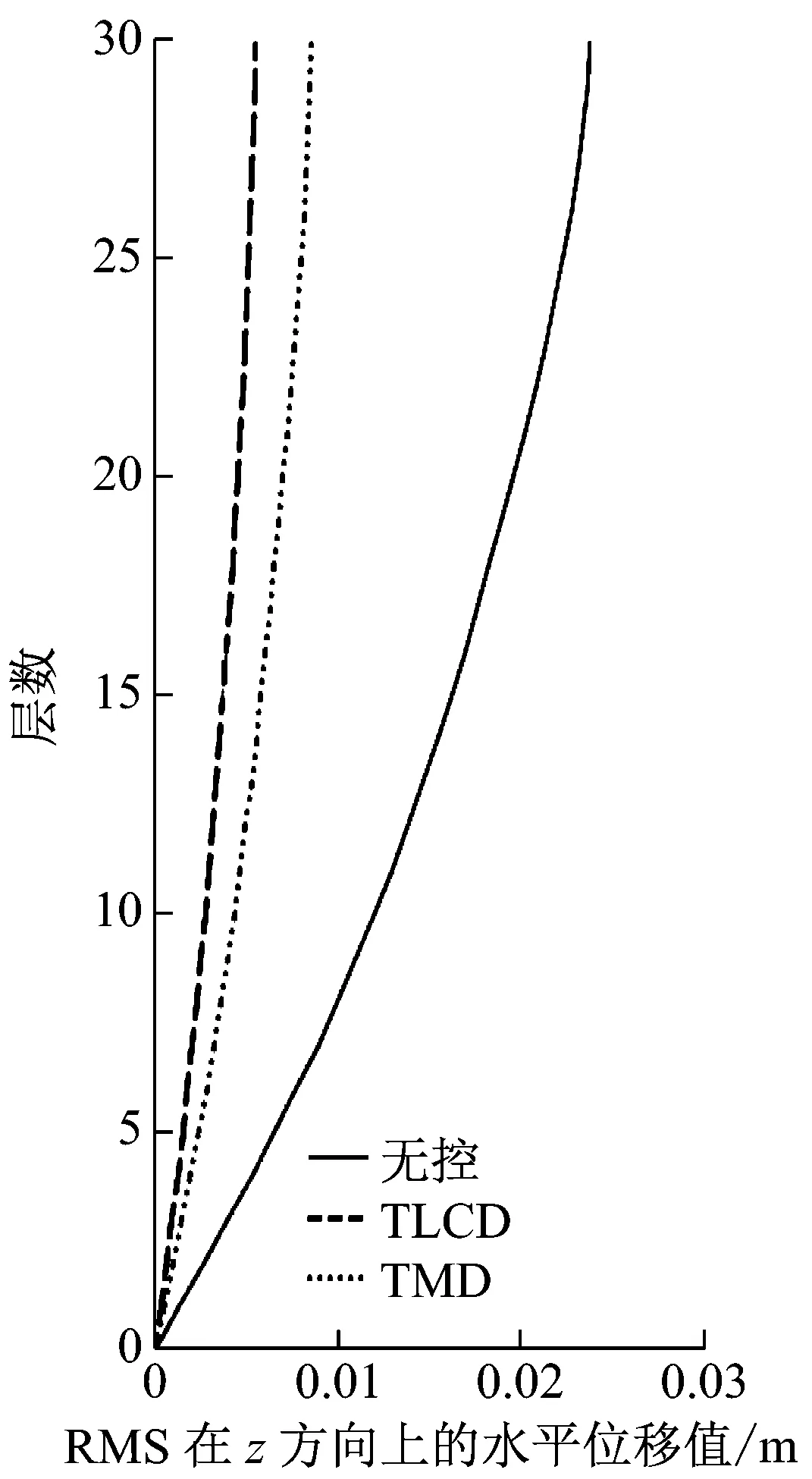
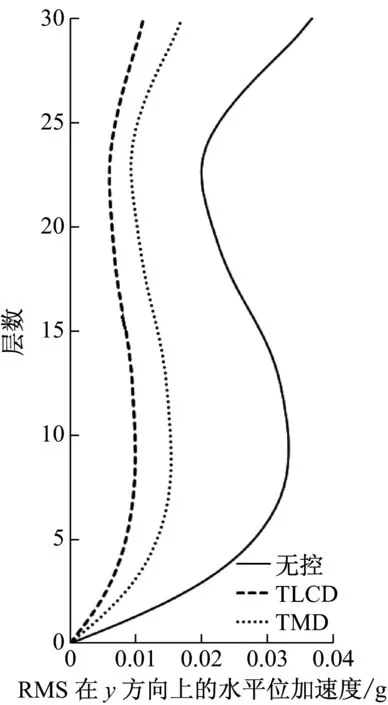
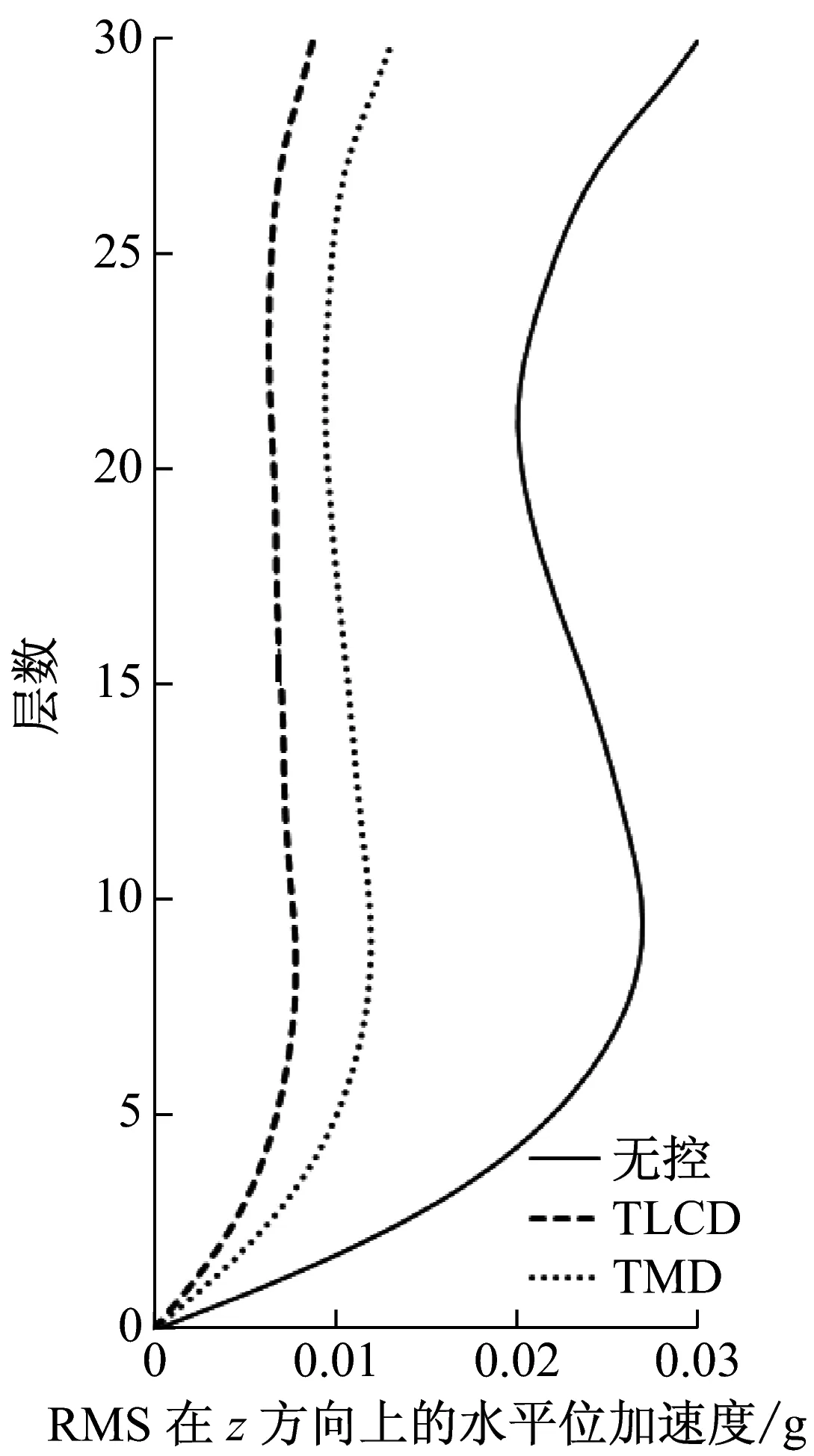
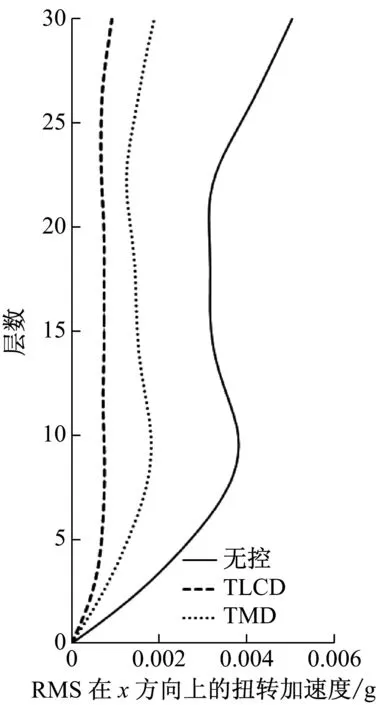
由于每个TLCD中水的质量大，导致截面面积比较大而不易制作，可将每个TLCD分为多个小截面TLCD，每个调谐比与阻尼比与设计一致。采用matlab软件对该非对称框架结构进行模拟计算，单向输入峰值为0.35g的El-Centro、0.146g天津和0.055g唐山地震波加速度记录，入射角与x轴夹角分别为0°、10°、20°、直至180°。图3～图8为入射角α=π/3原结构、安装TMD与安装TLCD后的楼层相对位移和绝对加速度均方根值(RMS值)响应图，按上述设计流程得到最优TLCD参数能达到最佳控制效果，且TLCD的减震效果要好于TMD的减震效果，减震率可达到60%以上。

表2 TLCD参数

6 结 论

通过对调谐液柱阻尼器最优位置、几何尺寸、参数优化和设计流程的研究，得出主要结论：

(1) 对于非对称结构宜采用模态瞬心的方法，并用遗传算法二次优化。

(2) TLCD质量比为1%<μ≤6%，倾斜角宜取π/4<β≤π/2，两段竖向管道截面一致，且尽量增加水平管段长度。

(3) TLCD参数优化设计采用将TLCGD/TTLCGD-结构体系转化为TMD/TTMD-结构体系的方法，利用Den Hartog公式对TLCGD/TTLCGD参数优化。

(4)TLCD参照给出的设计流程设计可提高阻尼器减震效果。

(a)

(b)

(c)

(a)

(b)

(c)

(a)

(b)

(c)

(a)

(b)

(c)

(a)

(b)

(c)

(a)

(b)

(c)

[1] HOCHRAINER M J. Tuned liquid column damper for structural control[J]. Acta Mechanica, 2005, 175: 57-76.

[2] DIANA G, RESTA F, SABATO D. Development of a methodology for damping of tall buildings motion using TLCD devices[J].Wind and Structures, 2013,17(6):629-646.

[3] 霍林生，李宏男.半主动变刚度TLCD减振控制的研究[J].振动与冲击, 2012,31(10):157-164.

HUO Linsheng, LI Hongnan. Structural vibration control using semi-active variable stiffness tuned liquid column damper[J]. Journal of Vibration and Shock, 2012,31(10):157-164.

[4] 钟振宇，楼文娟.设置非等截面TLCD高层建筑在风荷载作用下减振分析[J].浙江大学学报(工学版), 2013,47(6):1081-1087.

ZHONG Zhenyu,LOU Wenjuan.Vibration reduction of high-rise buildings with converted TLCD acted by wind load[J].Journal of Zhejiang University(Engineering Science),2013,47(6):1081-1087.

[5] 李宏男，董松元，李宏宇． 基于遗传算法优化阻尼器空间位置的结构振动控制[J].振动与冲击,2006,25(2):1-4.

LI Hongnan, DONG Songyuan, LI Hongyu. Optimum spatial placement of dampers in vibration controlled structures based on genetic algorithms[J].Journal of Vibration and Shock,2006,25(2):1-4.

[6] 吴学淑.平面不对称高层建筑结构利用速度型阻尼器减震控制的研究[D]． 上海: 同济大学，2008.

[7] 李春祥,许志民,张丽卿.主动调谐质量阻尼器对不规则建筑的减震行为研究[J].振动与冲击,2008,27(1):76-83.

LI Chunxiang, XU Zhimin, ZHANG Liqing.Earthquake reduction behaviors of active tuned mass dampers for an asymmetric building[J]. Journal of Vibration and Shock, 2008,27(1):76-83.

[8] 李宏男,霍林生,阎石.神经网络半主动TLCD对偏心结构的减震控制[J].地震工程与工程振动,2001, 21(4):135-141.

LI Hongnan, HUO Linsheng, YAN Shi.TLCD semi-active control for irregular building using neural networks[J].Earthquake Engineering and Engineering Vibration,2001,21(4):135-141.

[9] 张琴,曹立勇,楼文娟.基于LQR的黏弹性阻尼器参数优化方法[J].振动与冲击,2005,24(2):62-65.

ZHANG Qin,CAO Liyong,LOU Wenjuan.Parameter optimization of viscoelastic dampers based on the LQR theory[J]. Journal of Vibration and Shock, 2005,24(2):62-65.

[10] 李祥秀,谭平,刘良坤,等.基于功率法的TMD系统参数优化与减振性能分析[J].振动与冲击,2014,33(17):6-11.

LI Xiangxiu,TAN Ping,LIU Liangkun, et al.Parametric optimization and asesmic performance of a TMD system based on power method[J].Journal of Vibration and Shock,2014,33(17):6-11.

[11] ZIEGLER F. Mechanics of solids and fluids[M]. corr. Repr. 2nded. New York: Springer, 1998.

[12] 霍林生,李宏男,孙丽.多维地震作用下非对称结构利用TLCD减震控制研究[J].地震工程与工程振动,2001,21(4):147-153.

HUO Linsheng,LI Hongnan,SUN Li.Parameter study of TLCD control system excited by multi-dimensional ground motions[J].Earthquake Engineering and Engineering Vibration, 2001, 21(4):147-153.

[13] 杨润林,闫维明,周锡元.结构半主动控制研究中存在的若干问题[J].建筑结构学报,2007,28(4):64-75.

YANG Runlin,YAN Weiming,ZHOU Xiyuan.Key problems in semiactive structural control[J].Journal of building structures,2007,28(4):64-75.

[14] FU Chuan. Passive vibration control of plan-asymmetric buildings using tuned liquid column gas dampers[J]. Structural Engineering and Mechanics, 2009,33(3):339-355.

[15] LINDER-SILVESTER T,SCHNEIDER W. The moving contact line with weak viscosity effects-an application and evaluation of Shikhmurzae’s model[J].Acta Mechanica, 2005,176:254-258.