基于阻抗综合法的梁-圆柱壳耦合系统动态特性分析
周海军, 贺才春, 姜其斌, 李玩幽, 周常荣, 莫海枢
(1. 株洲时代新材料科技股份有限公司, 株洲 412007; 2. 哈尔滨工程大学 动力与能源工程学院, 哈尔滨 150001)
圆柱壳结构广泛应用在航空航天工程、船舶与海洋工程、核工程等领域。近几十年来,圆柱壳的动态特性引起了众多研究,并发展出一系列针对不同复杂影响因素的薄壳理论分析方法[1]。在工程应用中,圆柱壳经常与其他结构耦合使用,如刚性质量、环状结构、梁、板、舱壁等结构。
Zhang等[2]采用波传播方法研究了薄圆柱壳的振动特性,计算了一个长圆柱壳结构的频率并与FEM模型结果进行了对比分析。Li等[3-4]采用波传播方法研究了带环状加强结构的圆柱壳的自由振动,壳体的传播特性以及波传播方法的精确性。Zhou等[5]采用波传播方法研究了一般弹性边界条件下圆柱壳的自由振动特性,并研究了弹性边界对模态频率参数的影响。
Howard等[6]建立了一个刚性质量-被动/主动隔振器-圆柱壳体的模型,研究了振动能量由刚性质量向圆柱壳传递的特性。胡浩等[7]采用子结构导纳法研究了简支边界条件下带有多根弹簧-集中质量-圆柱壳耦合结构的自由振动。陈晓利等[8]利用薄板和梁的导纳公式推导了多加筋圆柱壳体在任意位置简谐力激励下的弯曲振动响应,并对特定参数的多加筋圆柱壳体的振动能量分布进行了数值仿真,结果表明振动能量在加筋处呈现急剧衰减。Lee等[9]采用子结构阻抗法研究了内部耦合了矩形板结构的简支圆柱壳的自由振动和功率流特性。
通过研究上述文献,并结合前期工作[10],本文针对水下结构物轴系至圆柱壳的结构,提出了一个梁-圆柱壳耦合模型,梁和圆柱壳的子结构分别采用改进的傅里叶级数方法(Improved Fourier Series Method,IFSM)[11]和波传播方法(Wave Propagation Approach)进行建模,两者之间的耦合则采用阻抗综合方法,结合所得到的子结构结果进行研究分析,所得结果采用有限元模型进行了验证。
1 梁-壳耦合模型及子结构分析
梁-圆柱壳耦合模型如图1所示,其中L和R分别为圆柱壳的长度和半径,l1、l2和m分别是梁结构的每跨长度以及梁上集中质量点的质量,kl和kr为耦合弹簧刚度,f(t)为作用在质量点上的简谐载荷。基于阻抗综合法,图1中的梁-壳耦合结构将分成梁和圆柱壳两个子结构进行分析。
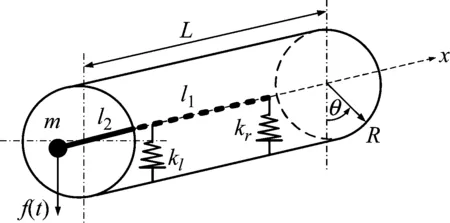
图1 梁-壳耦合模型
1.1 阻抗综合法[12]
一个拥有A和B两个子结构的耦合系统,其中子结构A上作用一简谐激励,如图2所示。假设此简谐激励为另一个子结构C。子结构A和B通过在2,3点处耦合。
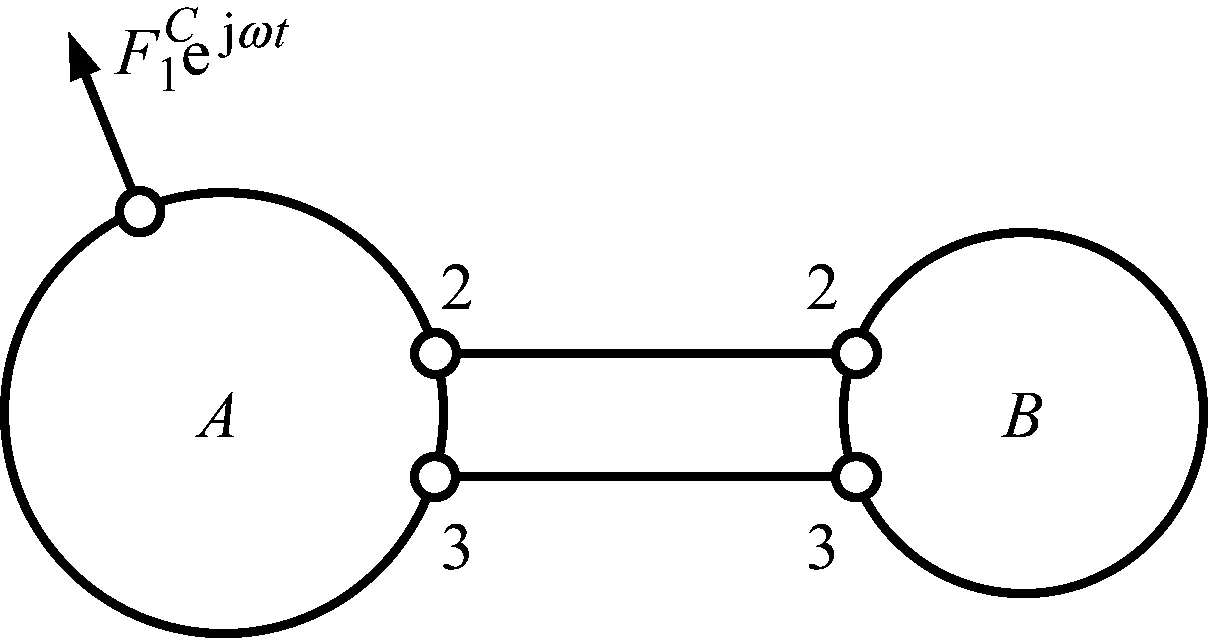
图2 拥有两个子结构的耦合系统
子结构A的动柔度运动方程可以表示为
(1)
将其写为矩阵形式
(2)
同理子结构B的运动方程为
(3)
其矩阵形式为
(4)
在系统2,3耦合点处的动力学相容和力平衡条件为
(5)
(6)
(7)
(8)
将式(5)和式(6)代入式(4),可得:
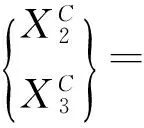
(9)
或者
(10)
其中
将式(10)代入式(1),可得:
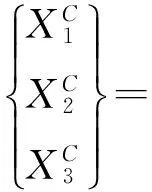
(11)
此时,通过求解式(11)可以得到
(12)
(13)
(14)
其中:
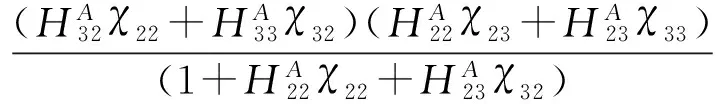
此时,将耦合点和激励点的响应表示成了各子结构的导纳形式。
1.2 梁子结构导纳分析
具有集中质量点的第i跨梁结构振动控制微分方程为
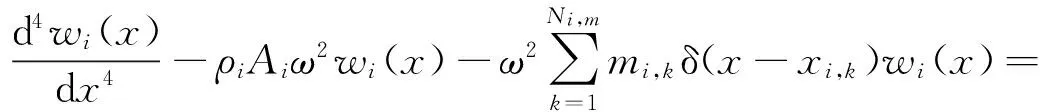
(15)
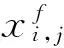
第i跨梁的弯曲挠度可表示为改进傅里叶级数的形式
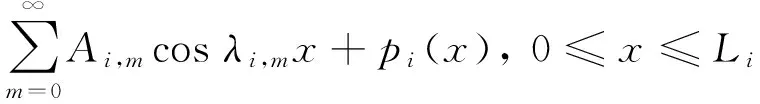
(16)
式中:pi(x)为加速余弦级数收敛的辅助多项式函数。
当考虑了边界条件之后,式(16)可以表示为
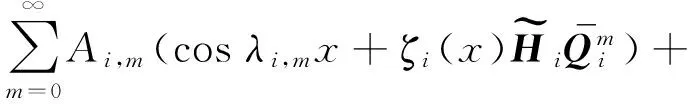
(17)
([Kij]-ω2[Mij]){Aj}={Fi}
(i,j=1,2……,N)
(18)
其中刚度和质量矩阵的单元表示如下
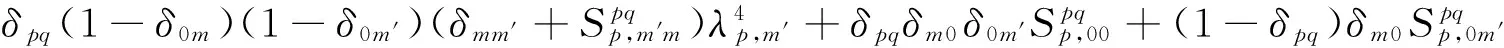
(19)
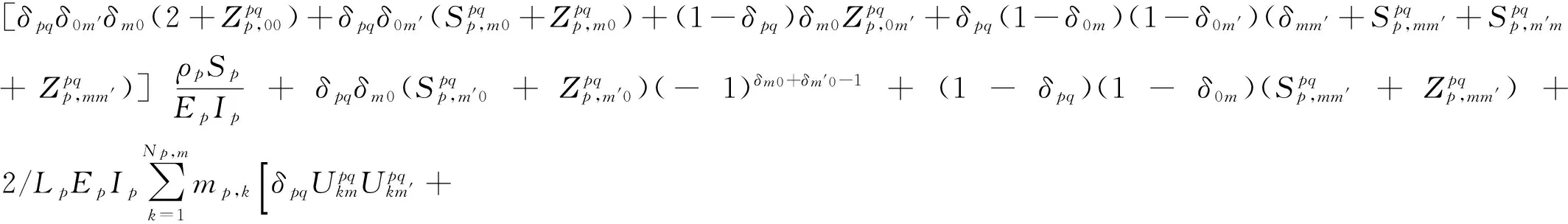
(20)
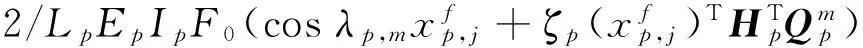
(21)
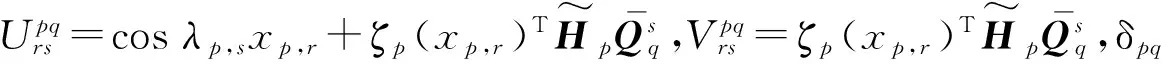
式(18)为一系列线性代数方程,根据已知的载荷可以求解得到未知的傅里叶系数。当系统为自由振动时,即式(18)右边激励向量设为0,则式(18)变为一个标准特征值问题方程,通过求解特征值方程可以得到方程的特征值和特征向量。当设置激励向量为单位力幅值时,即可通过式(18)求解得到多跨梁结构的导纳结果。
1.3 圆柱壳子结构导纳分析
基于Flügge理论,u,v和w分别表示壳体的轴向,周向和径向位移,此时薄壁圆柱壳的运动方程可以表示为
(22)
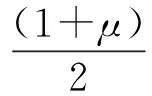
(23)
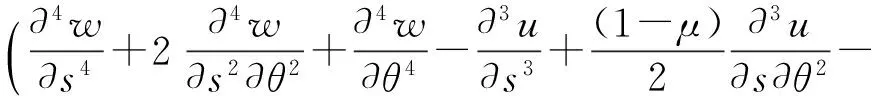
(24)
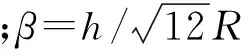
对于一个简支边界条件的圆柱壳,其位移可以表示为
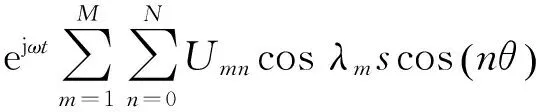
(λm=mπR/L)
(25)
(26)
(27)
式中:ω为圆频率;L为壳体长度;m和n分别为轴向和周向模态数;U,V,W分别为轴向、周向、径向位移幅值系数。
将式(25)~ (27)代入式(22)~ (24),分别将式(22)两边乘以cosλmscos(nθ),式(23)两边乘以sinλmssin(nθ),式(24)两边乘以sinλmscos(nθ),然后在0~2π及0~L/R上积分,利用三角函数的正交性可以整理得到如下矩阵形式的表达式:
(28)
其中,ms=2πRhLρ/4
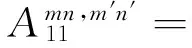
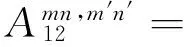
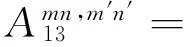
λmn2β2(1-μ)/2]
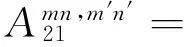
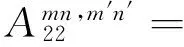
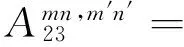
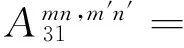
λmn2β2(1-μ)/2+μλm]=A13
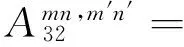
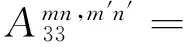
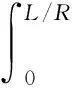
式(28)为一系列线性代数方程,根据已知的载荷可以求解得到未知的幅值系数,进而可以求得壳体的响应。当设置激励向量为单位力幅值时,即可通过式(28)求解得到圆柱壳结构的导纳结果。
此时,将得到的多跨梁及圆柱壳子结构的导纳结果代入式(12)~ (14),即可得到耦合结构的位移响应。
2 数值结果及其分析
2.1 结果验证及分析
如图3所示的梁-圆柱壳耦合结构,圆柱壳采用简支边界,而梁则通过弹簧与圆柱壳相连。圆柱壳结构参数如下:R=0.25 m,L=2 m,h=0.005 m,E=2.1×1011N/m2,ρ=7 850 kg/m3,泊松比为0.3;梁结构参数为:圆截面半径r=0.01 m,L=1 m,E=2.1×1011N/m2,ρ=7 850 kg/m3,泊松比为0.3。圆柱壳上联结点取为(sl,θl)=(0.5,0)以及(sr,θr)=(1.5,0),梁的联结点即为其两端点。
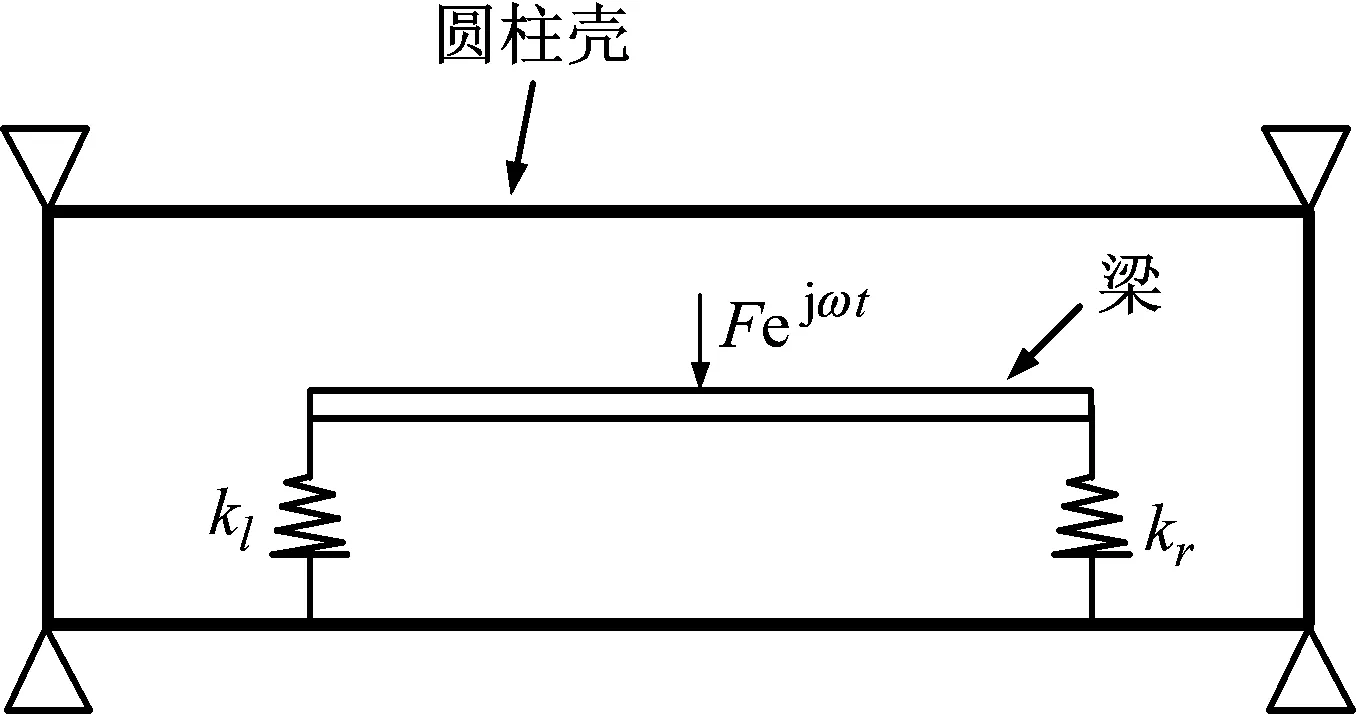
图3 梁-圆柱壳耦合结构
在梁结构中点施加一单位力简谐激励,频率范围为0~500 Hz,所得到的耦合结构激励点和耦合点的位移响应结果,以及与有限元模型所得结果的对比见图4,可以看出,二者结果除了在耦合点响应处反共振峰有一点偏移,其他都吻合得较好。
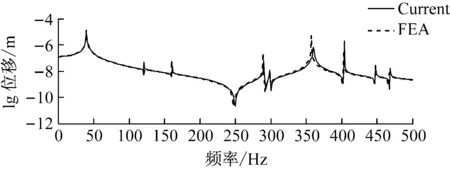
(a) 激励点响应
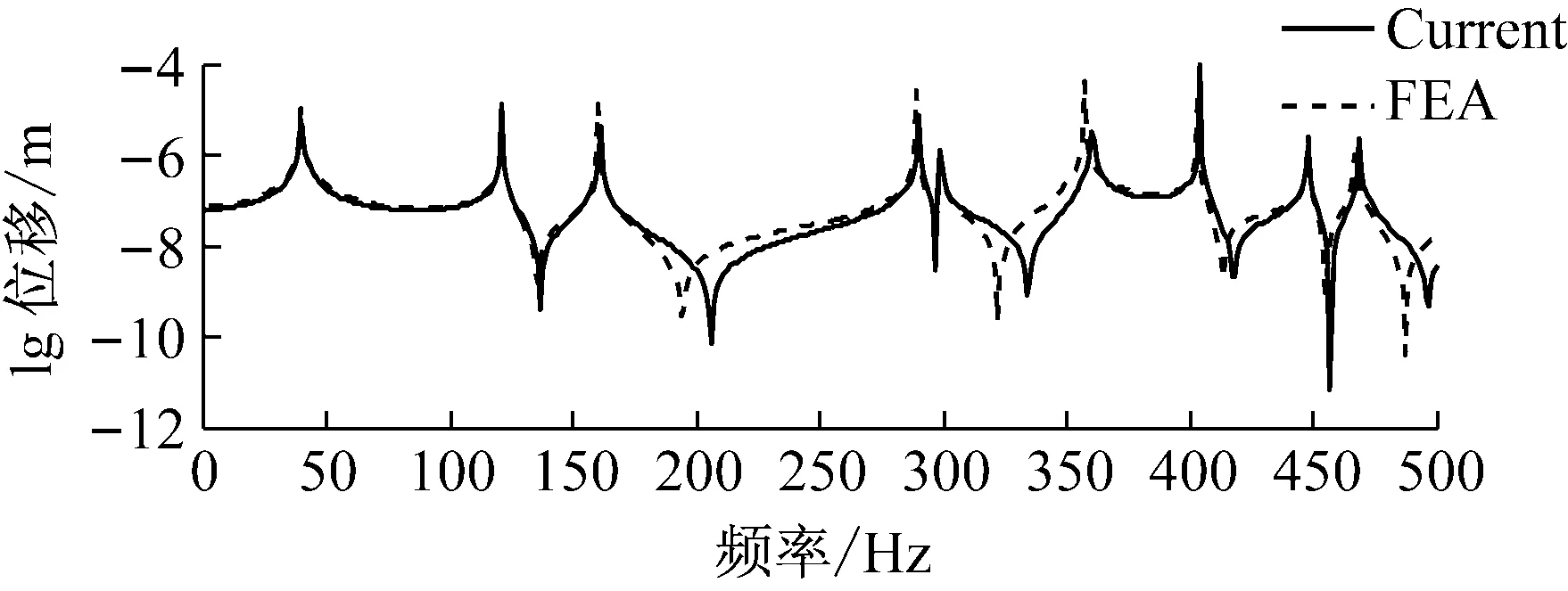
(b) 耦合点响应
经过分析可知反共振峰的偏移由于圆柱壳体轴向和周向模态数m和n的取值(M和N)收敛性引起的,如图5所示,随着轴向和周向模态数m和n的取值增大,共振峰快速收敛,反共振峰也体现出明显的收敛趋势。
可以看出,本文方法对梁-圆柱壳耦合结构的处理是正确的。
2.2 质量点-多跨梁-圆柱壳耦合结构分析
在图3结构的基础上,考虑悬臂梁及集中质量点的影响,如图6所示,悬臂梁跨长度:l2=0.6 m,集中质量点质量m=5 kg,其他参数同图3结构。单位力幅值简谐激励施加在质量点上,频率范围为0~500 Hz,所得质量点、左右两个耦合点的响应见图7。
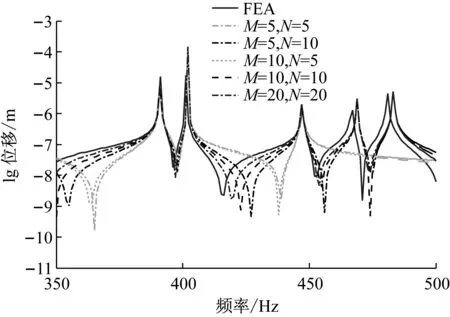
图5 圆柱壳收敛性分析
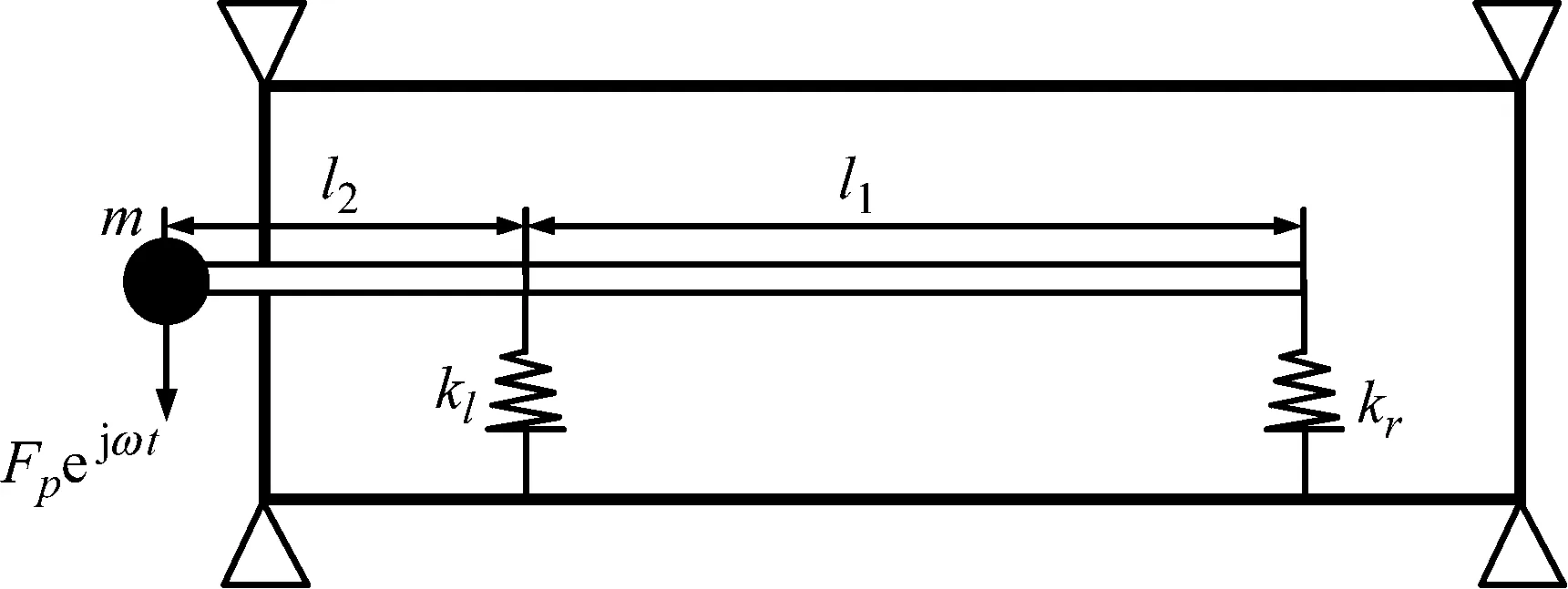
图6 质量点-多跨梁-圆柱壳耦合结构
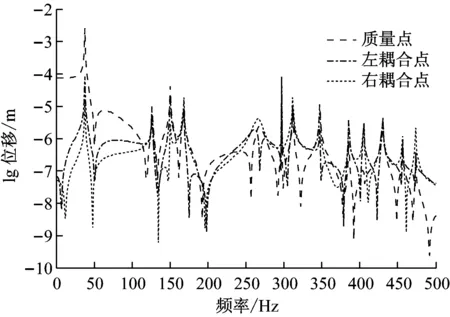
图7 质量点及梁耦合点响应
由图7可以看出:① 悬臂端质量点响应在低频段要大于耦合点的响应,而到高频后,三个位置的响应幅值基本相同;② 结构响应共振峰一致,这也符合结构固有频率的特性;而响应的反共振峰却各有不同。
然后改变悬臂端质量点质量及悬臂长度,分析其对结构响应的影响,重点分析质量点处的响应。如图8所示,为在悬臂长度l2=0.6 m的情况下,改变质量点质量的结构响应影响,质量点质量分别为4 kg、5 kg及5.5 kg,可以看出,影响不是很大。
如图9所示,为在质量点质量m=5 kg的情况下,改变悬臂长度的结构响应的影响,悬臂长度分别为0.4 m、0.6 m及0.8 m,可以看出,在0~50 Hz,三者变化不大,而再往高频段走,不仅响应峰值发生偏移,而且结构特性也随着响应峰值数量的改变而发生了变化。
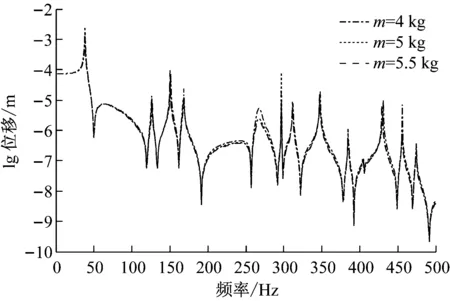
图8 质量点质量对耦合结构响应的影响
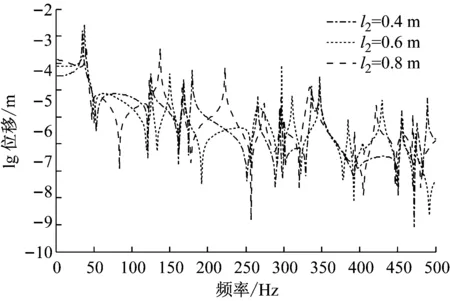
图9 悬臂长度对耦合结构响应的影响
可以看出,相对于悬臂端质量点质量,梁的悬臂长度对质量点-多跨梁-圆柱壳耦合结构的振动特性影响更大。
3 结 论
本文采用子结构阻抗综合法研究了梁-圆柱壳强耦合系统的振动特性。耦合系统分成了圆柱壳子结构和梁子结构,其中子结构可以有多种特征,如集中质量点、多跨等。通过求得的子结构导纳结果,耦合系统通过阻抗综合法直接求解系统响应,其中梁子结构的导纳结果采用改进的傅里叶级数方法获得,圆柱壳子结构的导纳结果采用波传播方法获得,并且其他方法获得的子结构导纳结果也适用于该综合方法。
通过与有限元模型所得结果的对比验证了该方法的正确性,并研究了一个集中质量点-多跨梁-支撑圆柱壳的耦合系统在质量点简谐激励下的振动特性,可知相对于悬臂端质量点质量,梁的悬臂长度对质量点-多跨梁-圆柱壳耦合结构的振动特性影响更大。
[1] LEISSA W. Vibrations of shells [M]. Washington, DC: NASA SP, 1973.
[2] ZHANG X M, LIU G R, LAM K Y. Vibration analysis of thin cylindrical shells using wave propagation approach [J]. Journal of Sound and Vibration,2001,239 (3): 397-403.
[3] LI Xuebin. Study on free vibration analysis of circular cylindrical shells using wave propagation [J]. Journal of Sound and Vibration,2008,311:667-682.
[4] GAN Lin, LI Xuebin, ZHANG Zheng. Free vibration analysis of ring-stiffened cylindrical shells using wave propagation approach [J]. Journal of Sound and Vibration, 2009, 326:633-646.
[5] ZHOU Haijun, LI Wanyou, LÜ Binglin, et al. Free vibrations of cylindrical shells with elastic-support boundary conditions [J]. Applied Acoustics, 2012, 73:751-756.
[6] HOWARD C Q, HANSEN C H, PAN J Q. Power transmission from a vibrating body to a circular cylindrical shell through passive and active isolators [J]. Journal of Acoustical Society of America, 1997, 101 (3):1479-1491.
[7] 胡浩,李正良,于伟. 带有弹簧-质量-圆柱壳耦合结构自由振动分析[J]. 振动与冲击,2016,35(7):209-213.
HU Hao, LI Zhengliang, YU Wei. Free vibration analysis for a spring-mass-cylindrical shell coupled structure [J]. Journal of Shock and Vibration, 2016,35(7):209-213.
[8] 陈晓利,盛美萍. 多加筋圆柱壳体振动特性的导纳法研究[J]. 振动与冲击,2007,26(4):133-135.
CHEN Xiaoli, SHENG Meiping. Vibrational characteristics of a multi-beam-stiffened cylindrical shell by mobility analysis [J]. Journal of Shock and Vibration, 2007,26(4):133-135.
[9] LEE Y S, CHOI M H, KIM J H. Free vibrations of laminated composite cylindrical shells with an interior rectangular plate [J]. Journal of Sound and Vibration,2003,265:795-817.
[10] 周海军,吕秉琳,王东华,等. 一种改进傅里叶级数方法的船舶轴系回旋振动动态特性研究[J]. 船舶力学,2012, 16(8): 962-970.
ZHOU Haijun, LÜ Binglin, WANG Donghua, et al. Research and analysis of gyroscopic vibration dynamic response of shafting based on an improved fourier series method [J]. Journal of Ship Mechanics, 2012, 16(8): 962-970.
[11] LI W L, XU Hong’an. An exact Fourier series method for the vibration analysis of multi-span beam systems [J]. Journal of Computational and Nonlinear Dynamics, 2009(4):0210011-0210019.
[12] 左鹤声. 机械阻抗方法与应用[M]. 北京:机械工业出版社,1987.

