辨析贝特朗问题中“一题多解”的误区

湖北省武汉市洪山区华中科技大学附属中学

马 俊 (邮编：430074)

在几何概型中，时常会遇到一些概率模型，通过不同的角度去分析得出不同的结果，并且师生在面对这种“一题多解”的困境时，只能抱着模棱两可的态度，给师生双方的教与学带来了很大的困惑.笔者结合教材中的例题、同行的研究以及自己的思考，谈谈自己对几何概型中“一题多解”的几点思考.

1 回顾历史 理清思路

贝特朗问题：在圆内任作一弦，求其长大于其内接正三角形边长的概率.

图1

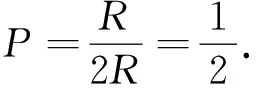
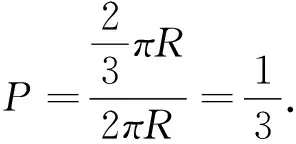
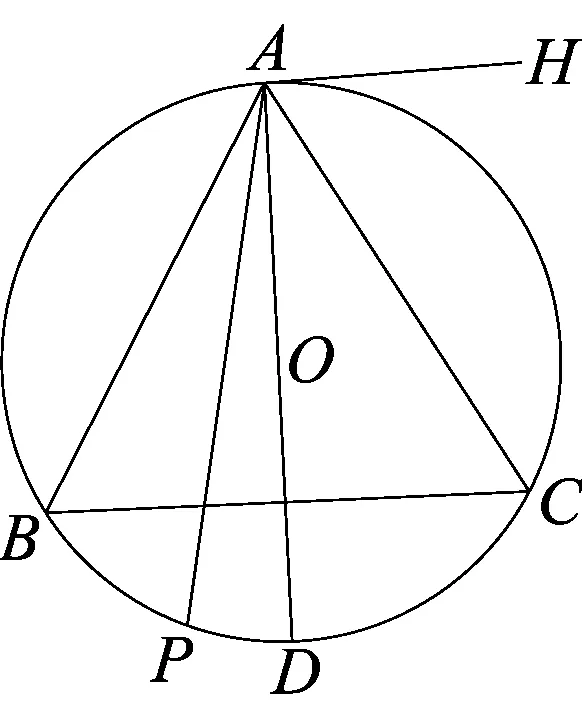
图2

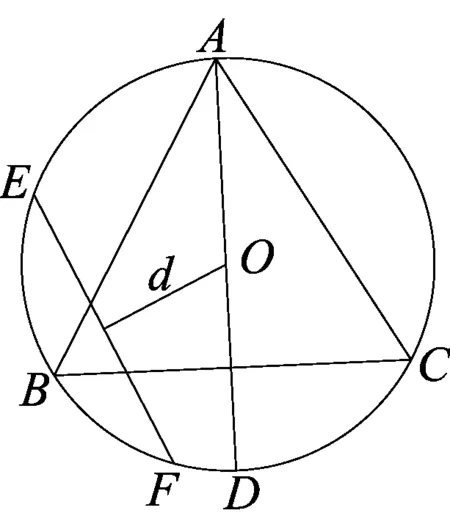
图3

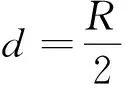
通过三种思路却得到了三种不同的结果，这与数学中一个概率问题只有一个结果是相矛盾的，但是每个思路又似乎合情合理.笔者对比贝特朗问题，从几个类似的问题进行探究.

2 对比探究 揭示缘由

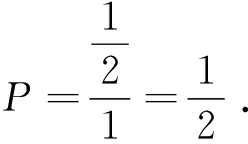
在这里需要说明的是几何概型通过一一映射变换后，得到新的概率模型依旧满足无限性和等可能性两个特点，即变换后仍然是一个几何概型.

在上面两个解法中已经得出了不同的结果，解法1是通过直接表示试验随机结果的变量(我们不妨把这个变量称之为真变量)来完成的，解法2是寻找一个能与真变量建立一一映射的变量(我们不妨把这个变量称之为假变量)来完成的.也就是说一一映射产生的假变量所计算的概率并不能真实反应几何概型中的概率.

为了进一步探究缘由，我们可以类比例1的思路来解决下面三个变式.

类比法2的思路，因为

B={y|y=x3,x∈A}=[0,1]，

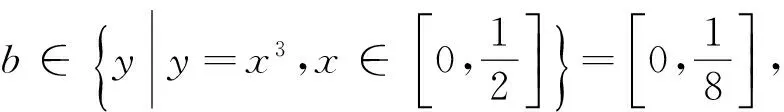
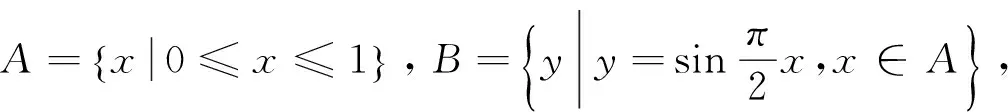
类比法2的思路，因为

B={y|y=x+1,x∈A}=[1,2]，

通过观察上面的例题和变式题，可以很直观的发现在思路1的基础上得到了相同的结果，而在思路2的基础上得到的结果却是各不相同.原因是思路1并没有使用集合B这个条件，而思路2使用了集合B这个条件，而由于集合B的中对应关系的不同而产生了不同的结果.其实细观题目，不难发现所求的概率其实与集合B毫无关系，例题和变式题的实质都是同一个问题(如下).

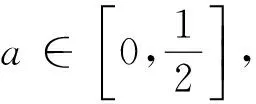
在这个问题解决中，建立一个一一映射的解题“思路”是何其之多，结果又将是何其之多.显然建立一一映射来实现几何概型的求解是一个误区，因此可以得到第一个命题.

命题1几何概型中，通过一一映射得到的新的随机事件概率并不能等价原随机事件的概率.

在变式3中，我们发现通过一一映射变换后得到的新随机事件概率却与原随机事件概率相等，难道这是一个巧合？通过对比不难发现变式3中的一一映射是一种线性变换，难道线性变换不会改变原随机事件概率？

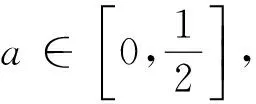
命题2在几何概型中，通过一一映射(线性)得到的新随机事件概率等价于原随机事件的概率.

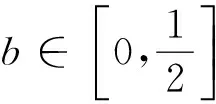
现在再来分析贝特朗问题，首先它的真变量是弦长，但是解法1中的变量是直径上任一点到圆心的距离，解法2中的变量是弦切角，解法3中的变量是任一点到圆心的距离，都是与真变量弦长建立的一一映射关系的假变量.

在解法2中，设∠DAH=θ，弦长AF=l，连接FD，

则在Rt△ADF中，l=2Rsinθ，θ∈(0,π)；

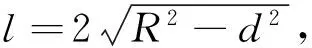
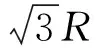
3 把握本质 避免误区

在教学中，几何概型的误区主要是源于对几何概型知识和本质理解不透彻所致，导致在解题时容易将问题凭主观转化成为另一个问题.因此在几何概型的教学中，需要充分尊重原问题，把握原问题中到底什么是直接表示实验结果的变量，切不可盲目转化，陷入“一题多解”的误区.

1 唐锐光.“一道几何概型问题的对话引起的思考”[J].中学数学教学参考(上旬)，2012(9):8-10

2 李文明.“追根溯源 释疑解惑”[J].数学通讯(教师版)，2014(9):28-31