曲线(线段)扫过的图形的面积问题

浙江省东阳市吴宁一中

王红鸣 (邮编：638400)

陕西学前师范学院数学系

赵小云 (邮编：230001)

数学教学中经常会碰到一类求线段或曲线扫过的面积的问题，本文就这类问题作一较系统的分析与讨论.

本文对线段和曲线按级命名，是基于它们所扫过的图形面积的计算中的难易程度来决定的.

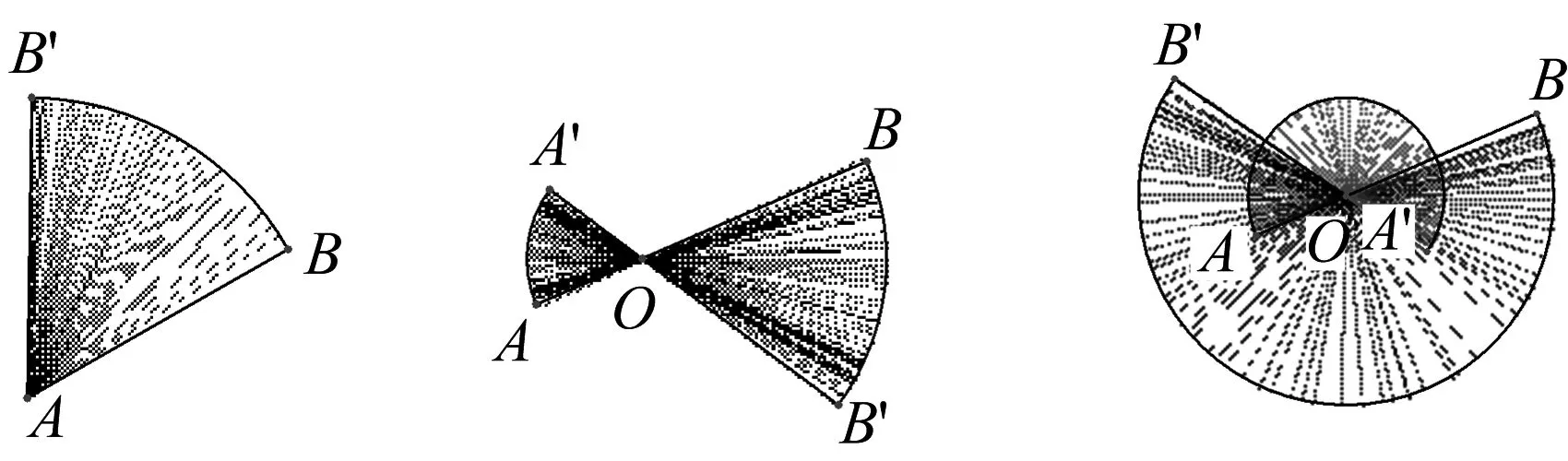
图1 图2 图2-1

1 线段的旋转

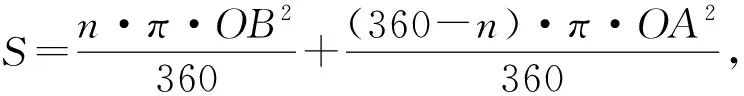
图3 图4 图5

二级线段一条线段，绕着延长线上的一个点旋转时，它就是一条二级线段.二级线段扫过的图形是一个扇环.图3中线段AB就是一条二级线段，其扫过的面积为

三级线段与四级线段一条线段，绕着旋转中心旋转，若旋转中心不在这条线段及其延长线上，且过旋转中心作旋转线段的垂线时，垂足在线段的端点或延长线上，那么称这条线段为三级线段，否则，就是四级线段.

如图4就是由三级线段AB绕着点O旋转时扫过的图形，其面积相当于图5中二级线段BC扫过的面积.

如图6中的线段AB，对旋转中心O来说就是四级线段，因为垂足C在线段AB上.它可以看做两段三级线段的组合，分别是AC和BC.

由于在旋转过程中线段AB扫过的面积有重叠，所以面积的计算较复杂，现作以下分类说明，并对要用到的一些量作如下设定：AC、BC、OC、∠BOC=x，均为已知量，AC>BC，旋转角度数为n.

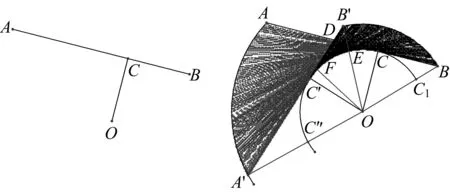
图6 图7

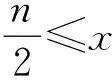
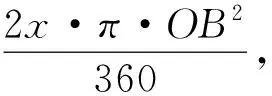
1.3 但随着旋转角的增大，又会出现新的重叠，如图9，这里的计算已超出初中生的学习目标和能力，所以在此不再多费笔墨.

图8 图9

1.4 特殊的，当旋转角为360度时，AB扫过的面积与AC扫过的面积相等,是π·(OA2-OC2).

2 折线(曲线)的旋转

一级折线(曲线)和二级折线(曲线) 一条折线(或曲线)，绕着某点旋转时，扫过的部分不会产生重叠时，我们称这条折线(或曲线)对这个旋转中心来说是一级折线(或曲线).否则就称它为二级折线(或曲线).

同一条折线是一级折线，还是二级折线，完全取决于旋转中心的位置.如图10中，折线ABC是点O的一级折线；而图11中，我们只是把旋转中心移动了一下，它就成了点O的二级曲线.

图10 图11 图12

定理1一级折线ABC扫过的图形面积等于三级线段CA扫过的图形面积，又等于二级线段CA′扫过的图形面积.如图12，证明略.

二级曲线旋转时扫过的图形有重叠，情况复杂，中考也不作要求，这里不讨论.

3 半圆是什么类型的曲线？

3.1 当旋转中心就是这个半圆的直径端点时，半圆是一级曲线.

定理2半圆弧是关于端点的一级曲线.(如图13)它扫过的图形的面积相当于直径(一级线段)扫过的图形的面积(如图14)

图13 图14 图15 图16

如图14是它扫过的图形，为了便于计算，将它分割成图15，图16是S2移到S3，最后将扇形外的弓形移到扇形内，这就说明半圆扫过的图形面积与一级线段AB扫过的图形面积是相等的.

3.2 当旋转中心在这个半圆的直径延长线上时，半圆还是一级曲线.

定理3半圆弧是关于直径延长线上的一点的一级曲线.它扫过的图形的面积相当于二级线段直径扫过的图形的面积.

3.3 当旋转中心不在直径的端点或直径的延长线上时，半圆是二级曲线，它在旋转时扫过的图形也较复杂，如图18.但是我们可以将它分割成两条一级曲线.

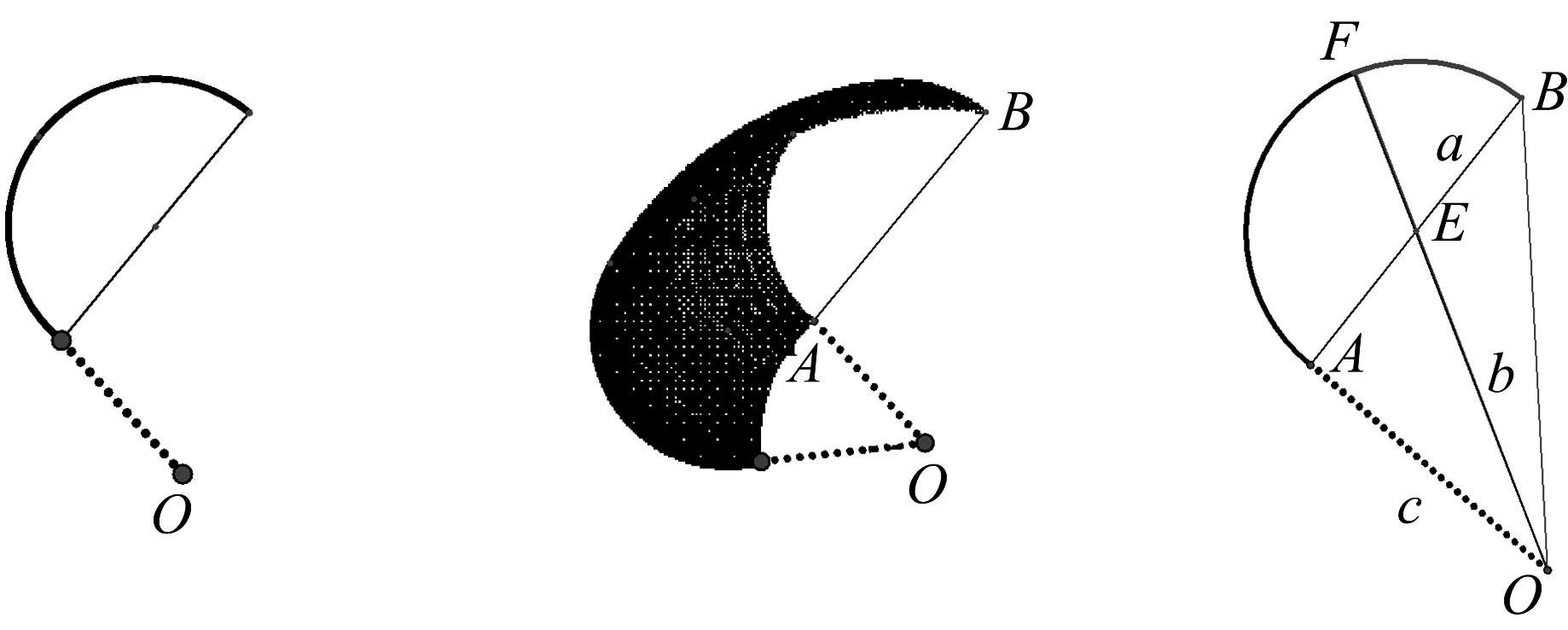
图17 图18 图17-1

如图17-1，设直径AB的中点为E，作射线OE交半圆于点F，则弧AF和弧BF都是关于点O的一级曲线.它们扫过的图形的面积分别可以转化为图19中的二级线段FH和二级线段BM扫过的面积，只要把重叠部分减掉即可.

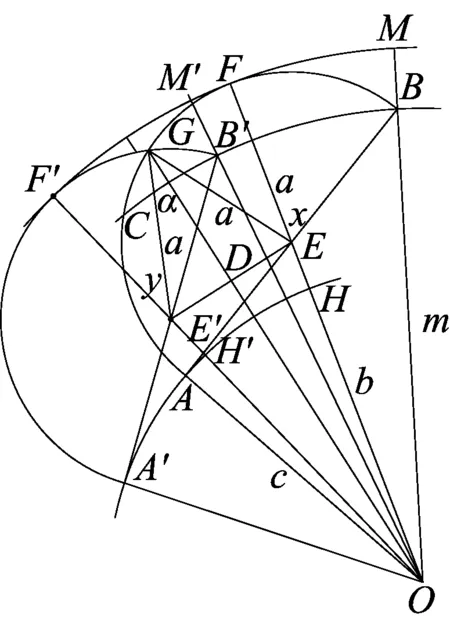
图19

在此图中，由于旋转角不大，重叠部分只是一个变形三角形，它等于扇形OFF′的面积减去扇形EFG的面积的2倍，再减去四边形GEOE′的面积.但需要以下已知条件：①旋转角∠BOB′=∠FOF′=n，②OB的长m，③半圆的半径a，④弧BF所对的圆心角度数x，⑤OE的长b，⑥OA的长c.图中∠α,可先在直角三角形OE′D中求出DE′，然后到三角形GDE′中求α，然后求出∠y.

当旋转角变大时，与图8、图9四级线段旋转时扫过的面积非常类似，这里不再论述.

4 结束语

(1)一级线段扫过的图形是扇形或两个扇形.

(2)二级线段扫过的图形是扇环.

(3)三级线段扫过的图形可以转化成二级线段扫过的图形.

(4)四级线段扫过的图形可以转化成两条三级线段扫过的图形，但有重叠，其面积计算存在着较大困难，初中生不宜.

(5)一级曲线扫过的图形可以转化成三级线段扫过的图形，直至二级线段扫过的图形.

(6)二级曲线扫过的图形可以转化成若干条一级线段扫过的图形，但有重叠，其面积计算存在着较大困难，初中生不宜.

(7)本文讨论的只是线段或曲线扫过的图形面积的计算，若将曲线的两个端点用线段连接，出现一个封闭的区域，区域扫过的图形与曲线扫过的图形是不一样的.