巧用空间向量突破立体几何问题

■河南省商丘市第一高级中学 胡 娜

空间向量是高考考查的重要内容之一,它也是解决立体几何问题的重要工具,在处理空间线线、线面、面面位置关系,以及夹角、距离等问题时起着至关重要的作用,有很多立体几何问题都可以用空间向量来找到巧妙的解决方法。

如何建立空间直角坐标系成了突破立体几何中的垂直、夹角等问题的关键。我们从以下几个例题进行剖析。

例1 如图1,在三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°。

(1)证明AB⊥A1C;

(2)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值。

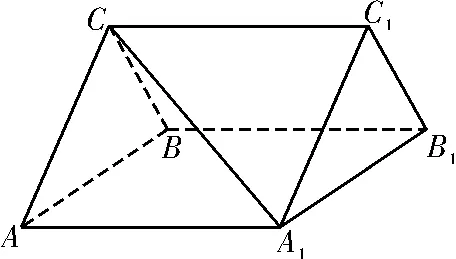
图1

突破点一：本题z轴的选取作为首要突破点,因为无论是从图像上看,还是从条件上分析,底面△ABC作为等腰三角形,底边的高线可以试着作为z轴。

突破点二：由于z轴已选取,而坐标原点是AB边的中点,所以x轴,y轴的选取我们应该考虑在平面AA1B1B内,由条件AB=AA1,∠BAA1=60°,从而连接A1O,x轴,y轴的建立水到渠成。

突破点三：准确无误表示关键点的坐标。

突破点四：法向量的求解。

解：(1)过点C作CO⊥AB,连接OA1,由于CA=CB,故OA=OB。又因为AB=AA1,且∠BAA1=60°,所以△AA1B为正三角形,则A1O⊥AB。又因为CO∩A1O=O,因此AB⊥平面COA1,所以AB⊥A1C。

(2)由于OA,OA1,OC两两垂直,故以O为原点,以OA,OA1,OC所在直线为x轴,y轴,z轴,建立如图2所示的空间直角坐标系,设OA=OB=1,则A(1,0,0),A1(0,3,0),C(0,0,3),B(-1,0,0),所以=(1,0,

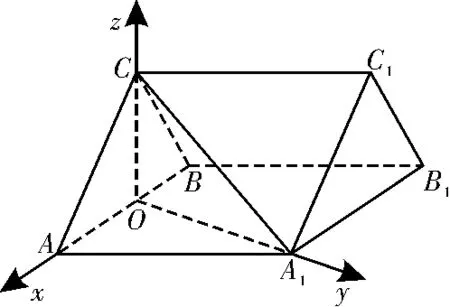
图2

例2 如图3,在四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,且AB=BC=2CD=2SD。

(1)证明SD⊥平面SAB;

(2)求AB与平面SBC所成角的余弦值。

突破点一：x轴,y轴的选取作为第一突破

点,由题意BC⊥CD,不妨把C点作为坐标原点。

突破点二：大胆作出z轴,因为只有S点的坐标与之有关系,而该点的坐标由条件可以求之,所以z轴的选择不需要纠结。

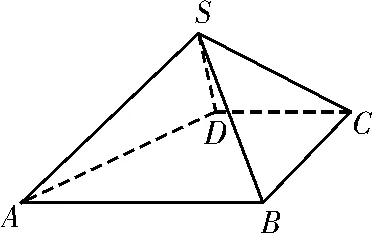
图3

突破点三：S点坐标的求解,因为有三个变量,即横坐标,纵坐标,竖坐标,理论上应该找出三组关系,而本题由于条件的特殊化,两组关系就够了,一个是侧面SAB为等边三角形,即,还有一个条件2CD=2SD(不妨设CD=1)。

突破点四：求出平面SBC的法向量。

解：(1)建立如图4所示的空间直角坐标系C-xyz,设SD=1,则D(1,0,0),A(2,2,0),B(0,2,0)。设S(x,y,z),则x＞0,y＞0,z＞0,因 此=(x-2,y-2,z)=(x,y-得 y2+x2=1。 又=2,所 以0,故DS⊥AS,DS⊥BS。又因为AS∩BS=S,所以SD⊥平面SAB。

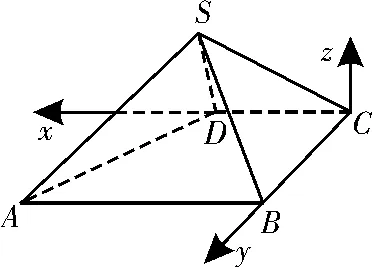
图4

例3 如图5,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C。

(1)证明AC=AB1;

(2)若AC⊥AB1,∠CBB1=60°,BC=AB,求二面角A-A1B1-C1的余弦值。

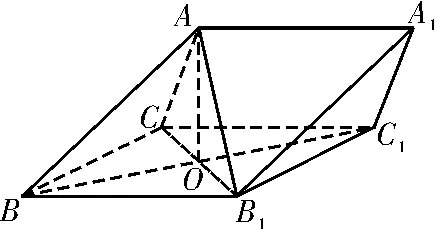
图5

突破点一：x轴,y轴的选取作为第一突破点,因为侧面BB1C1C为菱形,由对角线的垂直关系作为优先考虑的建系标准。

突破点二：z轴的准确定位,可以大胆猜想,设法证明。

突破点三：准确无误地表示关键点坐标。

突破点四：法向量的求解。

突破点五：二面角的平面角是钝角还是锐角的准确判定。

解：(1)连接B1C,BC1交于点O,再连接AO,由于侧面BB1C1C为菱形,因此B1C⊥BC1,且O是B1C和BC1的中点。又因为AB⊥B1C,且AB∩BO=B,所以B1C⊥平面ABO,故AO⊥B1C。又O是B1C的中点,所以AC=AB1。

(2)因为AC⊥AB1且O是B1C的中点,所以AO=CO。又因为BC=AB,所以△BOA≌△BOC,故OA⊥OB,这样OB,OB1,OA两两垂直。分别以OB,OB1,OA为x轴,y轴,z轴建立如图6所示的空间直角坐标系,设OB=1,由于∠CBB1=60°, 所 以△CBB1为等边三角形。因为BC=AB,所以

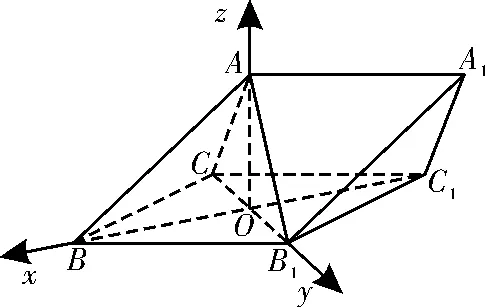
图6

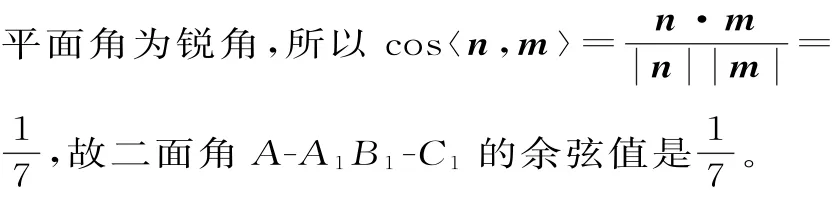
小结：空间向量在解决立体几何问题时扮演着重要的角色,但是要想灵活地应用,在解决问题时起到画龙点睛的作用,需要我们做到下面几点：首先,根据题设条件建立恰当的空间直角坐标系;其次,写出需要的点的坐标;最后,灵活运用需要的公式。