一种应用于大角度变换点云的配准方法

李 健，杨静茹，何 斌



一种应用于大角度变换点云的配准方法

李 健1，杨静茹1，何 斌2

(1. 陕西科技大学电气与信息工程学院，陕西 西安 710021；2. 同济大学电子与信息工程学院，上海 201804)

针对传统配准法不能很好解决大角度变换点云的配准这一问题，提出一种基于精确对应特征点对及其邻域点云的配准方法。首先分别计算两组点云的FPFH值，根据特征值建立点云间的对应关系；然后通过RANSAC滤除其中错误的匹配点对，得到相对精确的特征点对集合；之后通过KD-tree搜索的方式分别找出特征点对半径邻域内的点，应用ICP算法得到两部分点云的最优收敛；最后将计算得到的相对位置关系应用到原始点云上得到配准结果。通过对斯坦福大学点云库中Dragon、Happy Buddha模型以及Kinect采集的石膏像数据进行配准和比较，实验表明该方法能够有效解决大角度变换点云的配准问题，是一种具有高精度和高鲁棒性的三维点云配准方法。

点云配准；快速点特征直方图；随机采样一致；迭代最近点；KD-Tree

三维重建是计算机视觉中的一个重要组成部分，包含点云的采集、去噪、配准、融合、纹理映射等步骤，点云配准是三维重建中最重要也是最复杂的一步。现有的深度相机等三维测量设备一次只能测量物体一个方向上的数据，因此要得到物体的三维模型就必须将多次测量得到的点云数据通过配准合并成一个完整的三维模型。

点云配准这一概念自上世纪提出以来，涌现出了许多经典的算法。BESL等[1-2]提出的迭代最近点(iterative closest point，ICP)算法原理简单且易于实现，但需要为待配准点云提供一个较好的初值，否则迭代结果容易陷入局部最优。在基于特征的配准算法中，RUSU等[3]提出的点特征直方图(point feature histograms，PFH)计算方式通过多维直方图来描述查询点与邻域点之间的空间差异。PFH的改进算法称为快速点特征直方图(fast point feature histograms，FPFH)[4-5]，FPFH在降低算法复杂度的同时保留了PFH大部分的特性，但该方法容易生成错误的对应关系从而导致配准失败。在基于几何形状的配准算法中，4PCS算法[6-7]通过查找两个点集上全等且共面的四边形建立对应关系，但对于重叠区域较小的点集，通常难以找到对应关系。基于4PCS方法的Super4PCS算法[8]改善了这一问题，但其时间复杂度仍然远高于同类算法。

上述算法对于简单的点云配准问题大都能得到较好的效果。但实际的应用场景中，待配准的点云往往存在重合区域过小、点云间变换角度大等情况，传统算法在这样的场景下往往难以得到理想的效果。本文提出一种基于精确对应特征点对及其邻域点云的配准方法，融合FPFH、随机采样一致性(random sample consensus，RANSAC)算法[9]与ICP算法，基于PCL[10]实现，能够较好地解决复杂场景下的点云配准问题。

1 算法总体描述

当两片点云的初始位置变换角度过大时，难以通过一次配准就得到满意的结果，因此通常需要先经过粗配准步骤对两片点云进行初始配准，得到近似的旋转平移矩阵。在粗配准提供的良好初始匹配的基础上，精配准步骤通过进一步的计算能够得到两帧点云间更为精确的相对位置关系。本文方法分为粗配准和精配准两个步骤，具体流程如图1所示。

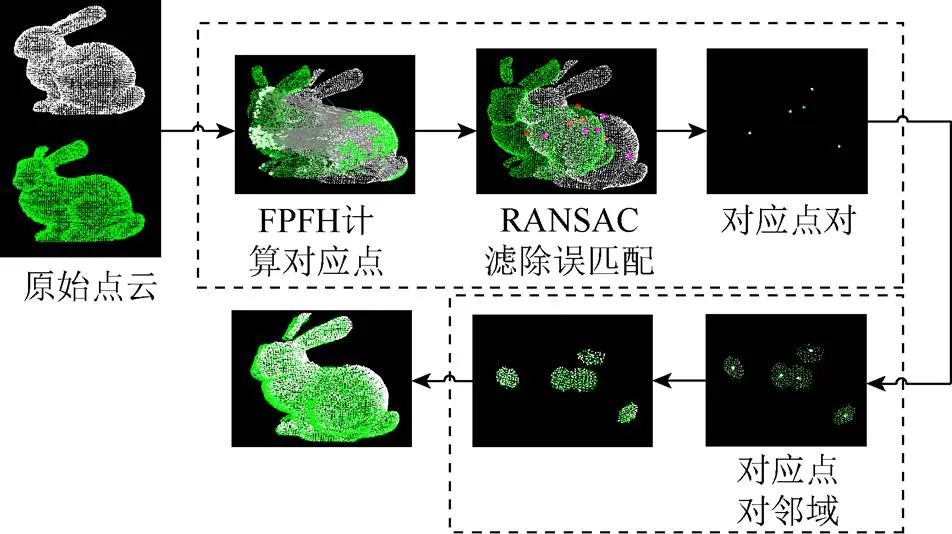
图1 本文算法流程示意图

图1中的原始点云分别为源点云和参考点云。在粗配准过程中，采用基于特征的FPFH方法得到初始对应关系，再通过RANSAC算法滤除误匹配，得到相对精确的对应关系。在精配准过程中，为减少计算量，采用KD-Tree搜索[11]的方式选取精确对应点对的半径邻域点云，应用ICP算法计算两部分点云的位置关系，将该变换关系应用到原始点云上得到最终的配准结果。

2 算法详细描述

2.1 基于FPFH的粗配准

粗配准采用基于快速点特征直方图计算方式的方法来实现，具体的步骤包括特征计算、误匹配筛除等步骤。

2.1.1 快速点特征直方图描述子搜索对应点

FPFH是一种空间局部点特征描述子，通过计算查询点与其邻域内元素的法线之间的关系来表示点云表面的变化情况，并通过一个多维直方图对点云的几何特性进行描述。FPFH计算的影响区域如图2所示。

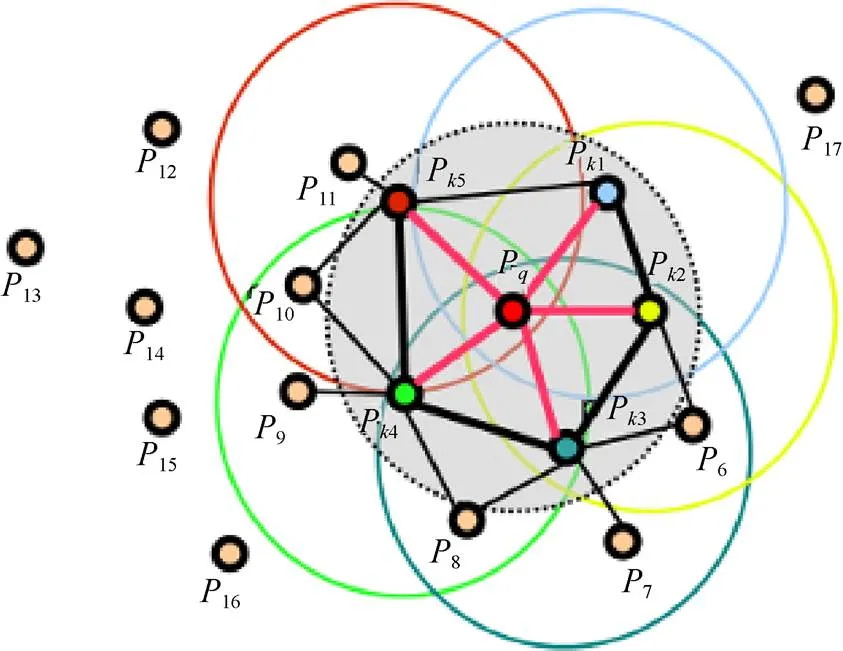
图2 FPFH影响区域示意图

查询点P位于图2中半径为的球形中心，查询点与其所有邻元素相互连接。为方便计算两点间的关系，在坐标系中计算任意两点P和P及与其对应的法线n和n之间的相对偏差。坐标系如图3所示。

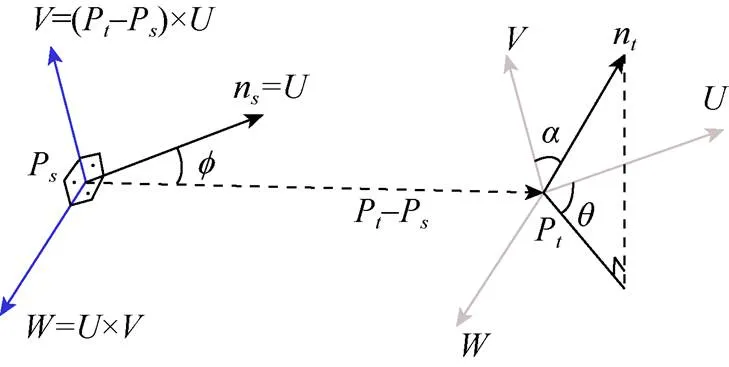
图3 UVW坐标示意图

3个方向分别用、、表示，其中

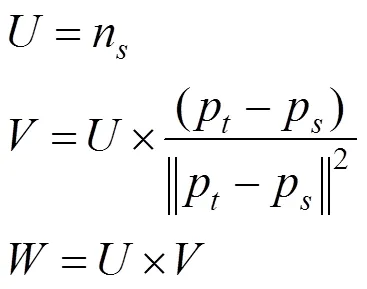
使用的坐标系，法线n和n之间的差可以化解为下面3个角度的差异，即

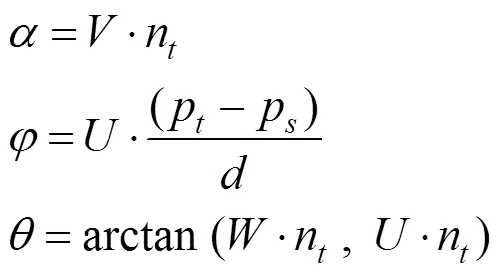
分别将、、从0°~360°等分为11个区间，创建一个有33个等分区间的直方图，每个区间对应特定范围内特征值的个数。按照如下步骤计算查询点的FPFH值：

步骤1.计算查询点P与其影响区域内所有点的3个特征值，统计每个区间所对应的特征值的个数，得到简化的点特征直方图SPFH。

步骤2.重新确定每个点的邻域，根据式(3)使用邻近的SPFH计算的最终FPFH。

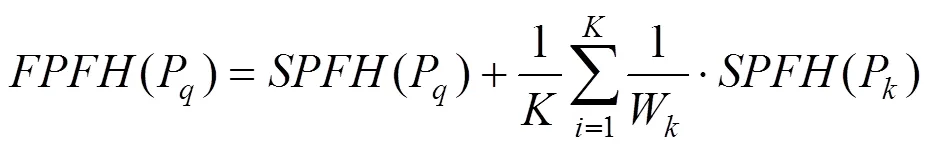
其中，P为P的邻域点；权重W是P与P之间的距离；为邻域点P的个数。

计算得到的快速点特征直方图如图4所示，图4(b)为4(a)中某点的快速点特征直方图。

2.1.2 RANSAC滤除误匹配

通过比较FPFH值得到的对应关系并不是完全正确的，采用RANSAC算法剔除其中的错误匹配，能够得到相对准确的对应关系。

RANSAC算法是一种简单有效的去除误匹配的方法，通过建立一个特定的数学模型将数据点分为“内点”和“外点”，采用迭代估计的方法计算出最优参数模型，找到的不符合该模型“外点”为误匹配点，符合模型的“内点”为精确匹配。以图5为例，图中实线对应正确匹配，线条两点为“内点”，虚线为误匹配，线条端点为“外点”。

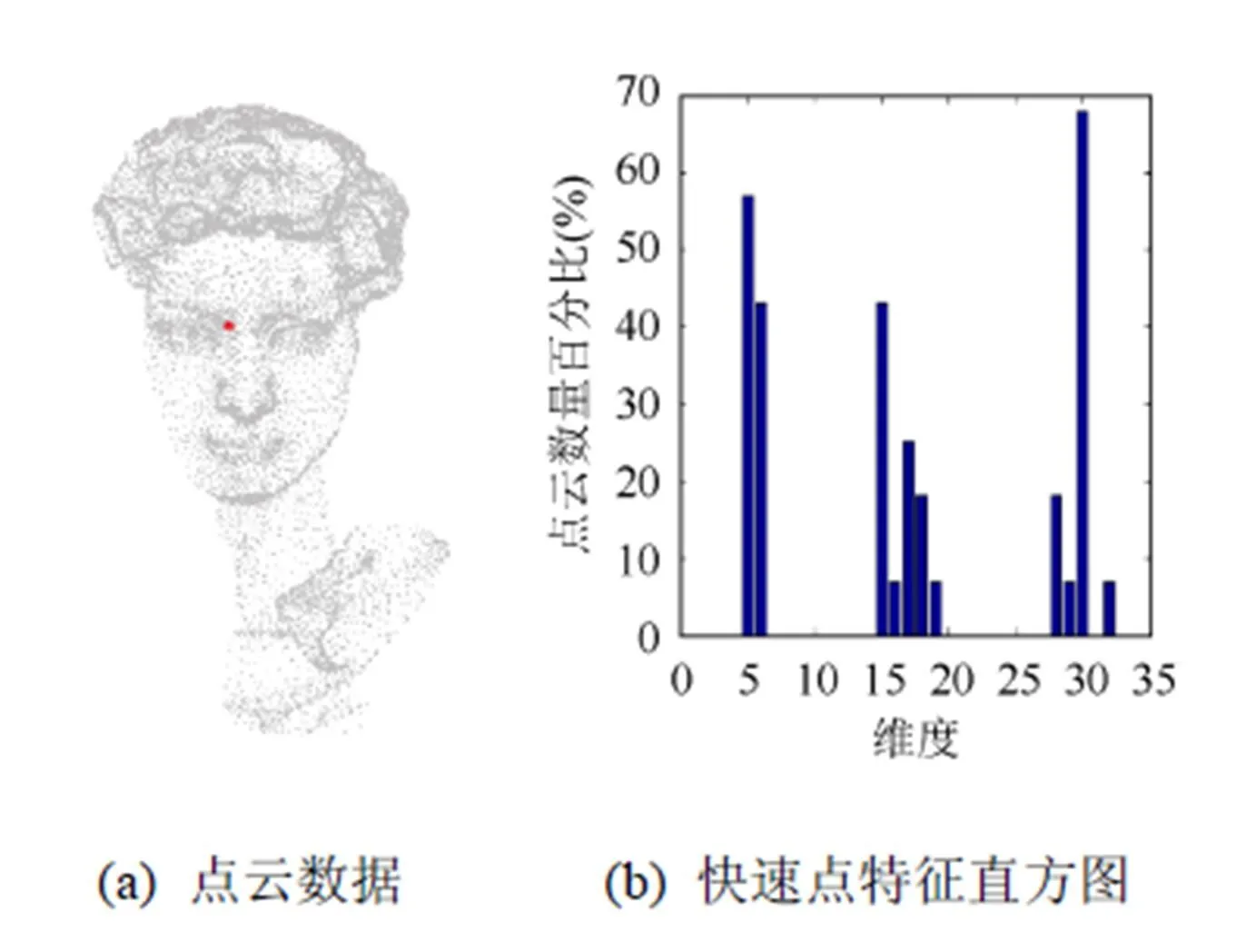
图4 快速点特征直方图示例

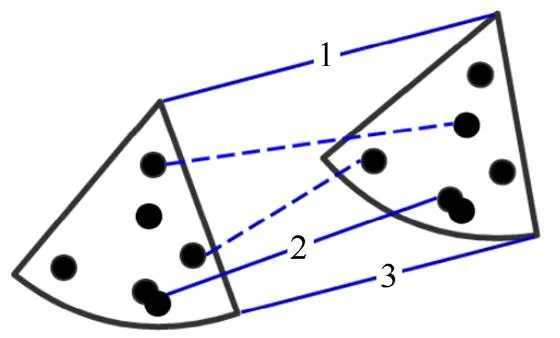
图5 RANSAC示意图

RANSAC步骤结束后可以得到较为正确的匹配关系。但由于FPFH计算方式描述的是查询点与其邻域点之间的关系，这一特性导致在点云表面曲率变化较小或者点云密集的区域中相邻点的FPFH值非常接近，因此可能会发生对应到正确匹配附近点的情况，如图5中2号对应关系所示，由于相邻点的FPFH值非常接近，所以根据特征值判定图5中2号线两端的点为对应点。该对应关系虽不完全准确，但却在RANSAC步骤所建立数学模型的容差范围内，所以认定其为正确匹配。这种不准确的映射关系会对配准结果产生负面影响，也是需要精配准步骤的原因。

2.2 基于关键点邻域的精配准

在粗配准所提供的初始匹配的基础上，精配能够进一步改进和完善配准结果。精配准分为基于KD-tree的关键点邻域搜索和ICP计算变换关系两个步骤。

2.2.1 基于KD-tree的关键点邻域搜索

粗配准步骤结束后，可以直接通过ICP算法计算点云的变换关系，但在已经得到较为精确的对应关系的前提下，通过KD-tree搜索的方式选择对应点邻域计算相对位置关系，可以节省计算成本。使用KD-tree搜索的方式选择对应点对半径内的点云计算最终的变换关系矩阵。

在具体的搜索过程中，将特征点作为查询点输入，给定查询点和查询距离的阈值(即查询半径)，从点云找出所有与查询点距离小于阈值的点。如图6所示，以空间中一点P为圆心，给定的查询距离为半径画球体，球体内点与P的距离小于半径的点即为所要查找的邻域点。

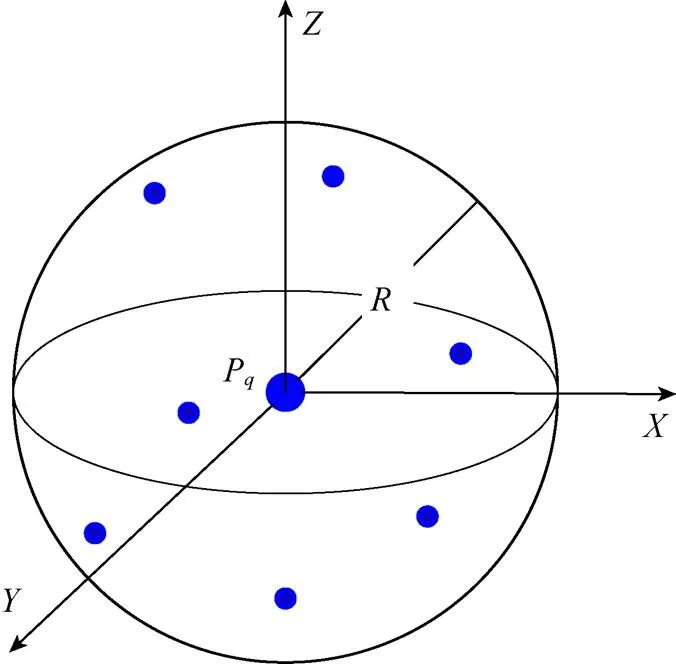
图6半径搜索示意图

2.2.2 ICP计算变换关系

通过半径搜索得到的对应区域是整体模型的一部分，只计算该部分点云的变换关系能够节约计算成本，将计算得到的、矩阵应用到原始模型上即可得到最终配准结果。

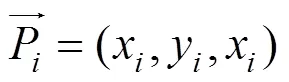
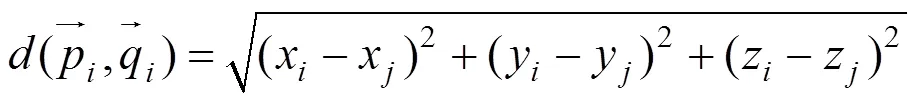
三维点云的配准问题可转化为求解使式(5)中目标函数最小时的和的问题，即

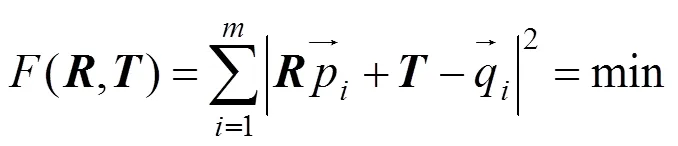
其中，为点集中对应点对的个数；、分别为旋转、平移变换矩阵。

3 实验结果与分析

本文以斯坦福大学三维点云库中Bunny模型为例，详细分析本文方法在实验中的具体步骤，并以斯坦福大学点云集中的Dragon、Happy Buddha以及Kinect采集的石膏像模型为例，将本文方法与ICP算法和Super 4PCS算法从配准效果和计算效率上做以对比。实验环境如下：

(1) 电脑配置：Intel Core i7-4790 CPU/8 G，RAM/AMD Radeon R7 250显卡/无GPU加速；

(2) 数据集来源：斯坦福大学点云集；

(3) 算法实现：PCL点云库/C++语言。

斯坦福兔子扫描数据Bunny000和Bunny045模型在初始状态下的位置关系如图7(a)所示，Bunny000和Bunny045是对同一个兔子模型分别从0°和45°扫描得到的点云数据，两片点云间含有部分不共有的数据。

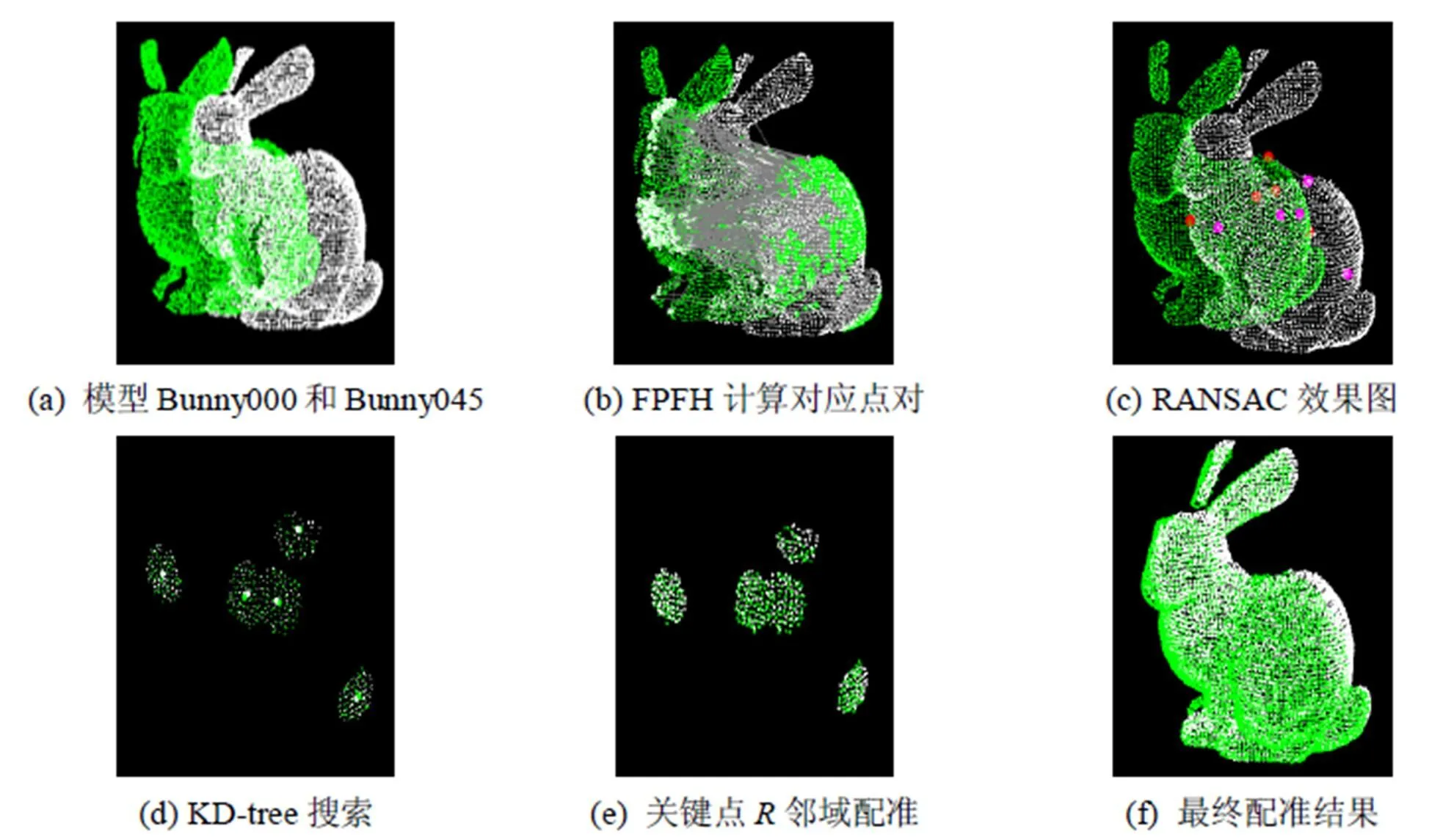
图7 实验步骤

在粗配准过程中：首先对图7(a)中的点分别计算其FPFH值，根据设定的阈值选择特征相近的点作为对应点对。图7(b)的连线为根据阈值筛选出的对应点对之间的连线，该对应关系并不完全正确。图7(c)为通过RANSAC步骤滤除误匹配后得到的对应关系。

在精配准步骤中：首先通过KD-tree搜索的方式找出特征点对半径邻域内的点，如图7(d)所示，图中的亮点为特征点，附近的点为其邻域点。图7(e)为选取图7(d)中的点分别作为目标点集和参考点集通过ICP算法进行配准得到的结果，图7(f)为在原始点云上应用图7(e)计算出的变换矩阵、得到的配准结果。

为验证本文方法的鲁棒性，选取了3种共计5组各具特色的模型进行实验。Stanford 点云集中的Dragon模型表面曲率变化较大且具有丰富的细节，选取Dragon中的Dragon0与Dragon24两帧数据在扫描时有24°的旋转，因此含有部分点云不共有的点。在此基础上将Dragon24模型分别沿、、轴旋转30°，平移0.05 m，模型位置关系如图8(a)所示。

图8(b)为本文方法的配准结果，图8(c)、8(d)分别为ICP和Super4PCS算法的配准结果。

图9的数据来源为Dragon模型中的Dragon0与Dragon48两帧数据，二者扫描时的角度差为48°，相比于图9中的数据，Dragon0与Dragon48的重叠区域更少。在此基础上，将Dragon48模型分别沿着、、轴旋转60°，平移0.1 m，得到图9(a)所示位置关系。图9(b)~(d)分别为本文算法、ICP算法和Super4PCS算法的实验结果。

与Dragon相比，Happy Buddha模型表面曲率变化相对平缓，但缺乏细节。图10中的数据来源为Happy Buddha模型中相邻的两帧数据Happy Buddha0与Happy Buddha24。

图8 Dragon0和Dragon24数据对比结果(下行为俯视图)

图9 Dragon0和Dragon48数据对比结果

图10 Happy Buddha0和Happy Buddha24数据对比结果(下行为俯视图)

Happy Buddha0与Happy Buddha24在扫描时的旋转角度为24°，在此基础上，将Happy Buddha24分别沿着、、轴旋转90°，平移0.15 m，得图10(a)中的初始位置关系。图10(b)~(d)分别为各算法对比结果。

图11中的数据来源为Happy Buddha模型中的Happy Buddha0与Happy Buddha48两帧数据，二者在扫描时的旋转角度为48°，相较于图11中的模型，重叠的点云数据更少。在此基础上，将Happy Buddha48模型分别沿、、轴旋转120°，平移0.2 m，位置关系如图11(a)所示，图11(b)为本文算法配准结果，图11(c)为ICP算法配准结果，图11(d)为Super4PCS算法的配准结果。

图11 Happy Buddha0和Happy Buddha48数据对比结果(下行为俯视图)

图12中的数据为手持Microsoft Kinect相机在随机角度上采集的两帧点云数据，点云未经滤波去噪等处理，初始位置如图12(a)所示。

图12(b)为本文算法配准结果，图12(c)为ICP算法的结果，图12(d)为Super4PCS算法的结果。

表1为本文算法与ICP算法和Super4PCS算法的对比结果。从图8~12中可以看出，ICP算法配准大角度变化点云容易陷入局部最优，从而导致配准失败。在对表1第一组数据Dragon0和Dragon24的配准中，相比于ICP算法，本文算法的RMS值降低了75.2%，相比于Super4PCS算法RMS值降低了42.0%，在时间花费上，本文算法花费时间高于ICP算法14.2%，但由于ICP算法配准失败，该数据不具有参考价值，Super4PCS所用时间为本文算法的7倍；在第二组数据中，本文算法的RMS相比于ICP和Super4PCS算法分别降低了62.2%、15.2%，花费时间为Super4PCS算法的11.8%；在第三组数据中，本文算法的RMS相比于ICP和Super4PCS算法分别降低了64.3%、36.1%，花费时间为Super4PCS算法的16.6%；在第四组数据中，本文算法的RMS相比于ICP和 Super4PCS算法分别降低了46.8%、6.5%，花费时间为Super4PCS算法的2.9%；在第五组数据中，本文算法的RMS相比于ICP和 Super4PCS算法分别降低了50.0%、6.3%，花费时间为Super4PCS算法的30.4%。综上所述，本文算法能够有效解决大角度变换点云的配准问题，并得到相对优于ICP和Super4PCS算法的结果。

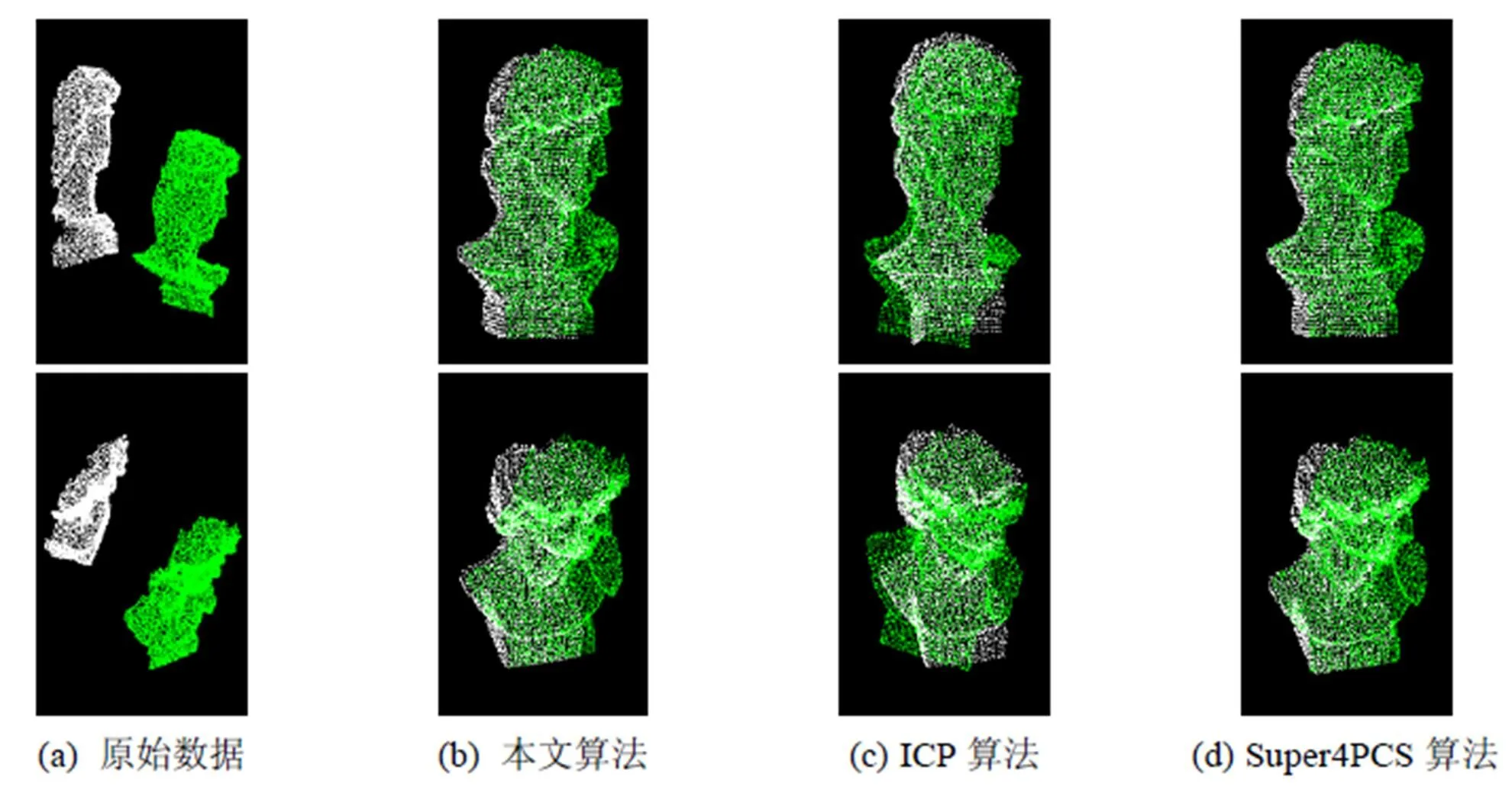
图12 Kinect采集数据随机两帧对比结果(下行为俯视图)

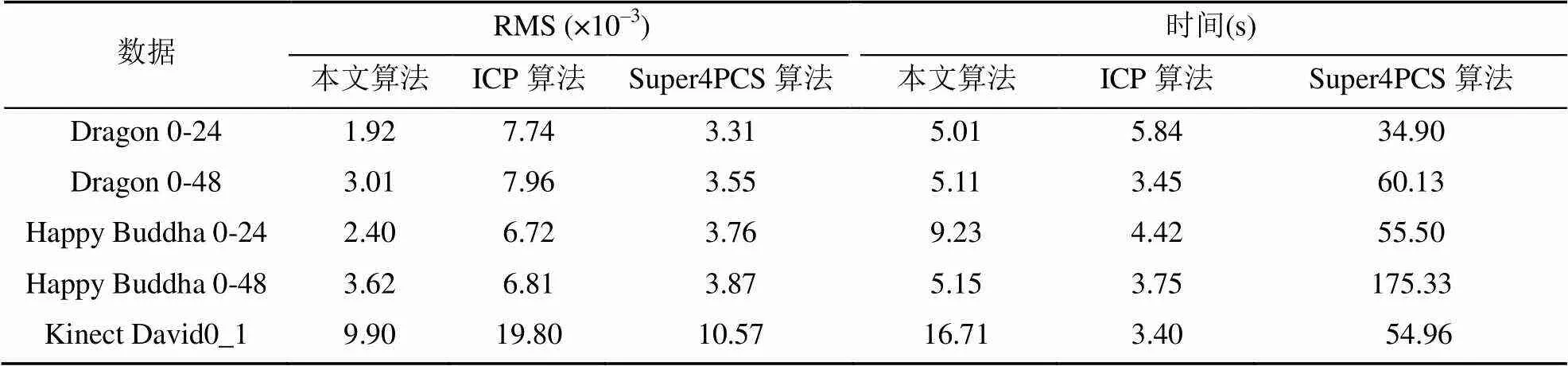
表1 算法对比表

4 结束语

本文通过总结和分析点云数据配准算法的研究现状，发现了点云配准中存在的大变换角度点云难以配准这一问题，提出了一种基于精确对应特征点对及其邻域点云的配准方法。通过利用点云的特征信息找出初始对应关系，再滤除掉错误对应点对得到粗配准结果，在此基础上选择精确对应点对邻域点云计算最优收敛。实验表明，该方法能够在节约计算成本的同时有效解决大角度变换、只有部分重合点云的配准问题。

[1] BESL P J, MCKAY N D. A method for registration of 3-D shapes [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-256.

[2] 赵夫群, 周明全. 改进的概率迭代最近点配准算法[J]. 图学学报, 2017, 38(1):15-22.

[3] RUSU R B, MARTON Z C, BLODOW N, et al. Learning informative point classes for the acquisition of object model maps [C]//International Conference on Control, Automation, Robotics and Vision. New York: IEEE Press, 2008: 643-650.

[4] RUSU R B, BLODOW N, BEETZ M. Fast point feature histograms (FPFH) for 3D registration [C]//IEEE International Conference on Robotics and Automation. New York: IEEE Press, 2009: 3212-3217.

[5] 马大贺, 刘国柱. 改进的基于FPFH特征配准点云的方法[J]. 计算机与现代化, 2017(11):46-50.

[6] AIGER D, MITRA N J, COHEN-OR D. 4-points congruent sets for robust pairwise surface registration [J]. Acm Transactions on Graphics, 2008, 27(3):1-10.

[7] 余文利, 周明全, 税午阳,等. 基于曲率的点云自动配准方法[J]. 系统仿真学报, 2015, 27(10):2374-2379.

[8] MELLADO N, AIGER D, MITRA N J. Super 4PCS fast global pointcloud registration via smart indexing [J]. Computer Graphics Forum, 2015, 33(5):205-215.

[9] CHUM O, MATAS J, KITTLER J. Locally optimized RANSAC [C]//Joint Pattern Recognition Symposium. Berlin: Springer, 2003:236-243.

[10] RUSU R B, COUSINS S. 3D is here: point cloud library (PCL) [C]//IEEE International Conference on Robotics and Automation. New York: IEEE Press, 2011:1-4.

[11] ANGELO L D, GIACCARI L. An efficient algorithm for the nearest neighbourhood search for point clouds [J]. International Journal of Computer Science Issues, 2011, 8(5):1-11.

A Registration Method for Large-Angle PointClouds

LI Jian1, YANG Jingru1, HE Bin2

(1. School of Electrical and Information Engineering, Shaanxi University of Science & Technology, Xi’an Shaanxi 710021, China; 2. School of Electronics and Information Engineering, Tongji University, Shanghai 201804, China)

To the problem of traditional registration algorithm are difficult to get the desired effect in large-angle pointcloud registration. We proposed a registration method based on exact correspondence feature point pairs and its-neighbour pointclouds. Firstly, calculate the FPFH of the pointclouds separately, establishing correspondences between point clouds According to the eigenvalues; Then remove the erroneous matching point pairs by RANSAC, and obtain a relatively accurate set of feature point pairs; Moreover, using KD-tree search get the-Rad region of the feature point pairs respectively, and applying ICP to obtain the optimal convergence of pointclouds. Finally, applying the ICP relative position relationship to the original pointclouds to get the final registration result. Through registration testing and comparison of the Stanford Dragon, Happy Buddha pointcloud models, and Gypsum data scanned by Kinect, The experiment shows that this method can effectively solve the registration problem of pointclouds with large angle transformation, its a 3D pointclouds registration method with high accuracy and robustness.

pointcloud registration; fast point feature histograms; random sample consensus; iterative closest point; KD-tree

TP 391

10.11996/JG.j.2095-302X.2018061098

A

2095-302X(2018)06-1098-07

2018-03-26；

2018-04-18

国家自然科学基金项目(51538009)；陕西省工业攻关项目(2015GY044）

李 健(1975-)，男，陕西蒲城人，教授，博士，硕士生导师。主要研究方向为计算机视觉、计算机图形学。E-mail：lijian@sust.edu.cn

何 斌(1975-)，男，安徽安庆人，教授，博士，博士生导师。主要研究方向为新型机器人动力学及智能控制、多种传感器技术与数据网络集成应用、大型复杂机构动力学与在线监测、图像检测与识别技术及应用。E-mail：hebin@tongji.edu.cn