初中数学动点问题的特殊解法

邬鹤

摘要：动点问题是初中数学的教学重点和难点，它对学生综合运用能力和解决复杂问题能力要求较高，学生往往会感到学习困难，存在恐惧心理。本文分析了初中数学动点问题的解题策略，旨在打开学生解决动点问题的思路，培养学生的发散思维。

关键词：初中数学 动点问题 特殊解法

动点问题一直以来都是中考数学的重要考点，也是初中生数学学习的重点和难点。通常来说，动点问题常常会综合多个模块的知识内容，如一次函数与几何图形结合、二次函数与几何图形结合等，然后将一个大主题细化成多个小问题，由浅入深地层层推进，对学生知识综合运用能力有着较高要求。动点问题的教学有利于促进学生数学思维、变通能力的发展，所以在解决动点问题时，学生要做到动中求静、以动制动、动静互化，从而探究出解决问题的方法。

一、动中求静

动点问题是指题设图形中存在一个或几个动点在图形线段、射线运动的开放性题目。如果在动点问题中有较多的不变量，那么在解答时学生要学会动中求静，找到问题中的不变量，并探寻其与变量之间的关系，以明确解题思路，探究解题途径。

例1.如图1所示，已知圆直径AB延长线上有一点动点P，过P點作圆切线，连接A点和切除切点C，过P点做∠CPA平分线，与AC线段相交于M点，问：∠CMP的大小？

在这道题中，虽然P点、M点为动点，但无论P点怎样运动，其与C点的连线都为圆的切线，这也意味着∠CPO角度不变，一直为90°。基于此，运用圆周角定理及外角定理即可得出无论P点在AB延长线上如何运动，∠CMP的大小都不会改变的结论，且可以算出该角的角度为45°。

二、以动制动

在动点问题中运用以动制动的解题思路，主要是借助函数图像描述动点变化轨迹，深入研究运动函数，建立图形变量函数关系，通过分析函数关系解决动点问题。

三、动静互化

动静互化的解题思路主要是指抓住图形运动变化中隐含静的瞬间，将问题特殊化，将动点在某些特殊位置形成的特殊关系明确展示，寻求问题中动静之间的内在联系。初中数学动点问题的特殊解法也通常以特殊位置为主，从而减少解题的盲目性，通过特殊位置得到的结论再进行反推，就能寻找结论成立的条件。

四、初中数学动点问题的特殊解法

在初中数学动点问题的解答中存在一些“投机取巧”的方法，如特殊值法、特殊点法等，根据动静互化的解题思想，通过特殊位置、特殊值先行获取结论，进而逆推找寻证实该结论的相关条件，这有利于学生在动中求静，灵活运用数学知识解决动点问题，进而促进学生发散思维。

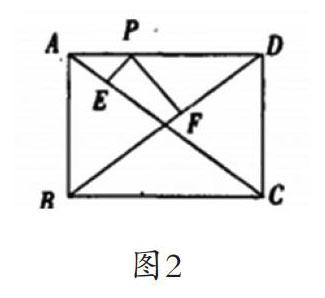
例2.如图2所示，已知矩形ABCD长为4厘米，宽为3厘米，在宽AD上有一动点P，连接PE、PF，E、F分别为PE垂直于AC的点、PF垂直于BD的点，求PE加PF的长？

由题目特点可以分析出，PE加PF长的肯定为定值，学生解题时可以将P点特殊化，如P点和A点或D点重合时，PE加PF长就是斜三角的高，可算出值为2.4厘米。

例3.如图3所示，已知直径为6的半圆弧上，有M、N两动点，AM、BN两弦相较于P点，求AP×AM+BP×BN的值？

我们可根据图形对称性解答此题，将M、N两动点位置特殊化，均为半圆的三等分点，使得AP、BP长度相等，进而求值，得出答案为36。

五、结语

初中数学动点问题具有复杂性、综合性较强的特点，通过解答动点问题，有利于培养学生观察和分析能力，促进学生发散思维，深化学生在解题中对各模块知识内容的理解，并利用特殊点的特殊解法，提高学生解决实际问题的能力。

参考文献：

[1]张国信，杨先智.例说初中数学动点问题的特殊解法[J].教育：文摘版，2016，（7）.

[2]陈韧.初中数学动点问题的解题策略分析[J].课程教育研究， 2018，（6）.

[3]王妮妮.初中数学动点问题的解题策略[J].新教育时代电子杂志：教师版，2016，（2）.

（作者单位：德兴铜矿中学）