数控加工曲面零件的误差分析与补偿技术研究
韩晓光,翟婷婷,付移风,郭奇
(中国航发西安动力控制科技有限公司,陕西 西安 710077)
0 引言
目前,零件曲面的数控加工主要采用三轴和五轴设备,同时零件的加工误差受诸多因素的影响,主要包括机床制造精度、加工刀具尺寸误差、机床热变形误差、加工切削参数以及加工工艺过程引起的误差等[1]。本文以如何减少数控编程、刀具和刀轴摆动引起的误差为出发点,通过对加工误差进行计算,提出了误差的的补偿方法。
1 加工误差分类
1.1 概述
在曲面零件的数控加工过程中,数控刀具以采用端铣刀、球头刀、环形刀为主,端铣刀是五轴设备加工曲面常用刀具,球头刀是三轴设备曲面加工常用刀具,环形刀主要适用于五轴设备加工[2]。本文以端铣刀加工单曲率曲面零件为对象,分析加工过程产生的误差。五轴数控设备加工零件曲面过程中,刀具轨迹采用直线插补运动时,刀具的中轴线将随加工曲面的法线进行不断的摆动。因此,加工误差由直线逼近误差δt和加工刀具端铣刀的刀轴摆动误差δn两部分构成[3]。
1.2 凸面的加工误差
1.2.1 直线逼近误差
在曲面零件加工过程中,通常将加工曲线轮廓划分为无限多个直线单元,通过直线单元拟合曲线轮廓。在直线插补段加工过程中,以直线段AB近似代替弧线AB,如图1所示。直线逼近误差δt的计算如下:在一个直线插补段内,设曲面弧线AB长为Δs,与其对应的弧度为θ,曲线曲率半径为kf,则有:
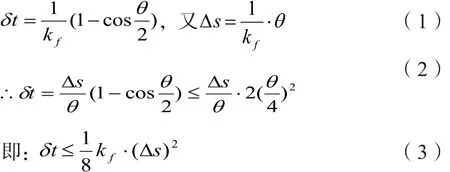
1.2.2 刀轴摆动误差
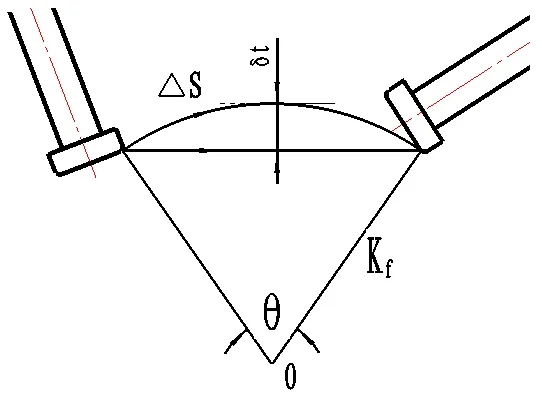
图1 直线逼近误差示意图Fig. 1 Linear approximation error schematic diagram

图2 端铣刀与凸面的位置关系图Fig. 2 Position relationship diagram between end milling cutter and convex surface
刀具刀轴摆动误差是指在数控切削过程中,端铣刀刀轴矢量摆动引起的误差,切削过程中端铣刀与凸面的几何位置关系如图2所示。刀轴摆动误差δn的计算过程可以分为以下几个步骤:
(1)建立刀具端面中心O的直线方程MN
采用两点式建立方程,可得:

式(4)中:R为端铣刀半径,xA、yA为切触点A的横、纵坐标,xB为切触点B的横坐标,θA、θB分别为刀具在切触点A、B处刀轴与y坐标轴的夹角[4]。
(2)建立刀具接触点K的轨迹方程
在一个直线插补段内,接触点K由点A到点B的切削运动过程中,刀轴线与y坐标轴之间的夹角θk不断变化,接触点K的运动轨迹可由接触点的纵坐标yk和刀轴线与y轴之间的夹角θk两个参数进行表示[5]。由图2可知:

(3)切触点K的轨迹凹凸性判定
当刀具中心O轨迹方程为MN时,由曲线的单调性、凹凸性定义可知,yk对x的一阶导数可以得到曲线的单调性和极值,yk对x的二阶导数可以得到接触点轨迹的凹凸性。
yk对x的一阶导数为:
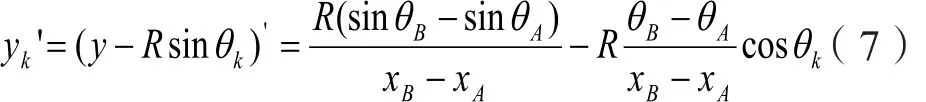
yk对x的二阶导数为:

可知:当θk>0时,,切触点轨迹为凹曲线;当θk<0时,,切触点轨迹为凸曲线;当θk=0时,,切触点在此时为凸、凹曲线的拐点[6]。
(4)刀轴摆动误差δn计算
应该求解产生的最大误差:
由,可知:
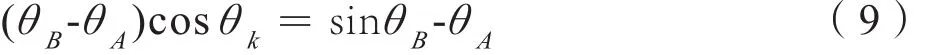
由上式可得:


当yk取最大值时,有代入式(11),可得:

由上述可知:接触点K的轨迹可能是凹曲线或凸曲线,刀轴摆动误差δn应取绝对值,可得:

(5)刀轴摆动误差δn表达式
如图3所示,θA、θB分别是一个直线插补段首末2点处的刀轴线与y轴之间的夹角,βA、βB分别为在A、B两接触点处的切线与刀具端面之间的夹角。分别过刀具中心点M、点N作平行于AB的直线,分别交接触点处的切线于A1、B1两点。
在ΔAA1M中,可得:同理,在ΔBB1N,可得将θA、θB代入式(13),可得:

故总误差为:
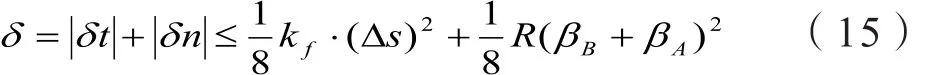
1.3 凹面加工误差
加工凹曲面时的直线逼近误差δt同凸曲面加工相同,如图4所示。即为:
庭院水体的特点是小而精致,以其独有的摄人魅力满足人们追求自然、亲近自然的向往.水景的位置、水面的大小、水位的深度是设计的重点,在做水景设计时既不能做得太深又不能太浅,这就要求在满足人们亲水性、生态美观性、经济性要求的前提下,还要综合考虑老人、孩子的安全等.
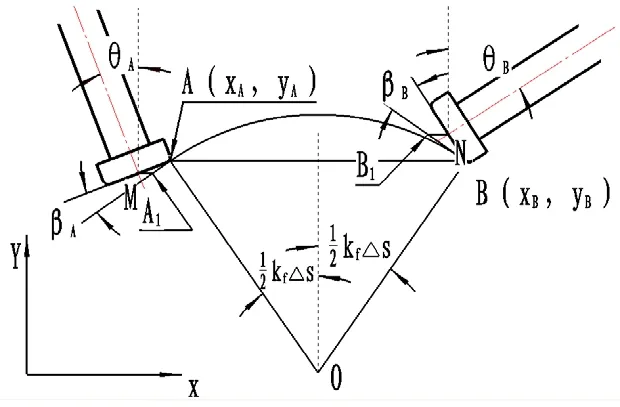
图3 刀轴摆动误差示意图Fig. 3 Schematic diagram of tool shaft swing error

图4 端铣刀与凸面的位置关系图Fig. 4 Position relationship between end milling cutter and convex surface
加工凹曲面刀轴的摆动误差在直线逼近误差之内,其求解方法同加工凸曲面的方法,同时,由于此时|δn|总小于|δt|,因此总的误差为:

1.4 误差影响因素
由上述分析可知,曲面零件的加工误差主要由直线逼近误差δt和刀轴摆动误差δn两部分构成[7],同时,在直线插补段的中点处的误差最大。直线逼近误差δt与加工所用刀具无关,只与所加工曲面的形状有关,且于所加工曲面的法曲率kf、插补段的曲面弧长Δs的平方成正比;刀具刀轴摆动误差δn既与加工所用刀具半径R、加工曲面曲率kf、曲面弧长Δs有关,还与刀具在切削过程中切入曲面的位置关系有关[8-9]。
2 误差补偿
2.1 直线逼近误差补偿
由式(3)可知,采用直线插补拟合曲线加工产生的直线逼近误差为。在切削加工过程中,曲线的曲率kf是不可控参数,弧长△s是可控参数,由切削刀具走刀步长L来近似代替,式(13)可写为:

通过控制走刀步长L对直线逼近误差进行有效控制,同时,对任意指定的直线逼近误差极限ε,当 |δt|≤ε时,有,可求得走刀步长:

可得出:根据加工曲面的精度要求,在允许的加工误差范围ε内,控制切削走刀步长L就可实现对直线逼近误差的控制。
2.2 刀轴摆动误差补偿

图5 刀轴摆动误差补偿示意图Fig. 5 Schematic diagram of tool axis swing error compensation

图6 切削步长设定Fig. 6 Cutting step setting

图7 切削公差设定Fig. 7 Cutting tolerance setting
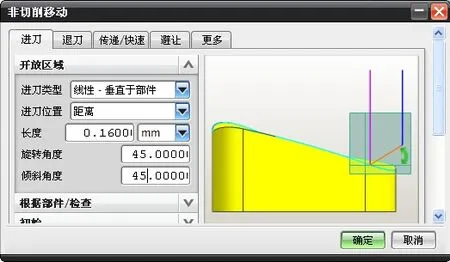
图8 非切削运动参数设定Fig. 8Non-cutting motion parameter setting
当加工曲面沿刀具进给方向为凸曲线,即kf>0时,刀具接触点的运动轨迹仍然为凹曲线,此时的加工误差达到较大,最大值为直线逼近误差与刀具轴线摆动误差绝对值之和[10],即:δ=|δt|+|δn|,此时需要对加工误差进行补偿,加工误差的补偿方法如图5所示,将刀具接触点在一个直线插补段的起点A沿加工曲面在A点处的法矢量方向平移一段距离至A1点,经过计算,使得,此时最大误差值为直线逼近误差δt,可以有效地控制加工误差。
当加工表面沿走刀方向为凹曲线,即kf<0时,刀轴摆动误差δn小于直线逼近误差δt,无需误差补偿。
3 实例验证
为验证上述方法有效性,选择X-11零件进行加工验证。选用φ6端铣刀,转速4000 r/min,进给1000 mm/m,曲率半径为160 mm,θ=20,通过式(3)计算,得δt≤0.31,取δt=0.31,根据直线逼近误差补偿步长计算公式式(18)计算,得步长L≤0.05 mm,取L=0.05 mm,在切削参数中设置切削步长0.05 mm,如图6所示,参数设置如图7所示。在非切削移动对话框中设置进刀路径为线性沿矢量[11],矢量为在切削区域起点处的法矢量,通过摆动误差补偿公式计算,设置距切触点距离0.16 mm,如图8所示。

图9 验证实物图Fig. 9 Diagram of verifying physical objects
通过实物加工验证(图9),零件的曲面加工加工误差可有效控制在0.1之内,满足零件的加工要求。
4 结论
通过对五轴加工中心加工曲面零件产生误差的理论分析,建立了产生误差的数学模型,提出了误差补偿的控制方法,通过软件编程仿真及实物加工验证,经验证误差补偿办法可行、有效,误差补偿办法的提出为高效率、高精度加工曲面零件提供了依据,对曲面薄壁件的高精度加工具有指导意义。

