认清实质 探索规律——《探索规律》教学点滴总结

四川省巴中市巴州区第三小学 何金莲

规律是事物之间内在的必然联系，是客观存在的，它决定着事物发展的趋向。规律往往“躲藏”在现象背后，需要深入挖掘才会浮现出来。

数学是研究数量关系和空间形式的科学。数学学习的过程离不开对数量关系和空间形式的规律的探寻。探索规律的过程是不断明晰数学思想方法、逼近数学本质的过程，是培养合情推理和演绎推理能力、发展创新意识和品质的过程。

探索规律的教学必须首先明确规律的隐蔽性，通过激趣、猜测、验证、领悟、运用等多个环节的“光合作用”，让规律在学生心中生根、发芽，让探索规律的过程在学生以后的学习、生活中开花、结果，从而使学生的推理能力得到发展。

探索规律的一般步骤是：具体问题→观察、猜想→推理、分析→表达规律→验证→得出结论。笔者在长期的小学数学教学中，概括出了几类“探索规律”题目的规律探索方法，现予以总结，希望对以后的教学工作有所帮助。

一、与序数相关的规律

点拨：分母是前一个的3倍，分子都是1。

例2：观察一串数，3、5、7、9……到第n个数是___

点拨：3=2×1+15=2×2+1

7=2×3+19=2×4+1

答：2n+1

点拨：分数的分子分别是21=222=423=8 24=16……，分数的分母分别是21+ 3 =522+ 3 =723+ 3 =11 24+3=19

二、与周期性相关的规律

例4：观察下列一组数的排列1、2、3、4、3、2、1、2、3、4、3、2、1……，则第2008个数是____

点拨：从第1个数“1”到第六个数“2”共6个数为一个循环周期，周期计算：2008÷6=334……4，即，2008个数中有334个整周期还余4个数，第2008个数为一个周期中的第四个数。

答案：4

例5: 3的正整数次幂：31=332=933=27 34=8135=24336=72937=218738=6561，观察归纳可得32007的个位数字是____

点拨：3n的个位数是3、7、9、1四个一循环2007÷ 4 =501……3，则32007与33的个位数字一样，是7。

答案：7

三、几何图形的规律

例6：如图把同样大小的黑色棋子放在正多边形的边上，按照这样的规律摆下去，则第n个图形需要黑色的棋子的个数是多少？

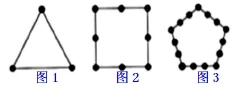
点拨：第一个图形3条边，共3=1×3，第二个图形4条边，共8=2×4个棋子，第三个图形5条边，共15=3×5个棋子……，第n个图形需要黑色棋子的个数是n(n+2)颗。

答案：n(n+2)

例7：用火柴棒按下列图中的方式搭图形（每一边放一根火柴）

第n个图形要多少根火柴棒

点拨：图形① 3根，图形② 3+2×1根

图形③ 3+2×2根 图形④ 3+2×3根

∴第n个图形：3+2（n-1）=3+ 2n-2=2n+1（根）

答：2n+1根。

例8：观察下列图形，他们是按一定规律排列的，依照此规律，第n个图形有多少个?

例9:如图

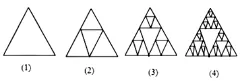
第五个图形应该有____个三角形

点拨：第三个图形可以看成是第二个图形的3倍再加上中间和外面的两个三角形，有17个，第四个图形可以看成是第三个图形的3倍再加上中间和外面的两个三角形，有53个，所以第五个图形可以看成是第四个图形的3倍再加上中间和外面的两个三角形，有161个。

答：161个

探索规律的教学绝不会止步于总结出规律，必须让学生运用规律解决问题，而在运用规律的过程中，往往会有新的发现，从而丰富原有的规律，发现新的规律。学生在用中学，学中用，教学过程由学生的思维过程推动，规律也在运用的过程中不断完善和丰富。