一类多个平行传染阶段分数阶SEI传染病模型的Lyapunov函数

郑 义, 赵新俊*

（石河子大学理学院数学系, 新疆 石河子 832003）

数学模型可以用于描述流行病的传播，对疾病的预防以及控制起着重要的作用。在传染病动力学中，主要采用的是由Kermack与McKendrick在1927年所建立的SIS和SIR仓室模型[1]。对于狐狸狂犬病、在家禽中传播的布鲁氏杆菌、AIDS等此类疾病，易感者被感染之后不会立即发病具有传染力，而是先成为潜伏者，在潜伏期过后才会变为感染者具有传染力，在潜伏期内潜伏者可能会远离疾病传播中心对其他人群分别进行传染。为研究此类疾病传播规律建立的模型为SEI流行病模型。

随着数学理论的发展，经典模型得到了不断的变化与改进[2-3]，近年来分数阶微积分被广泛应用到生物数学等一些领域[4-6]。随着分数阶微积分被引入流行病动力学中，依据分数阶微积分所建立的模型具有整数阶所不具备的性质[7]。Korobeinikov[8]讨论了多个平行传染阶段SIR和SEIR传染病模型的全局稳定性；Aguila Camacho[9]等提出了Caputo型分数阶导数的求导公式，解决了平方型函数的分数阶求导问题；Vargas-De-Leon C[10]提出了Volterra 型Lyapunov函数的分数阶求导公式。这些研究都对于构造Lyapunov函数来证明平衡点的全局稳定性提供了很大的帮助。

本文考虑多个平行传染阶段的分数阶SEI流行病模型，对模型进行分析得到模型的平衡点与阈值，通过构造相应的 Lyapunov函数来讨论平衡点的全局稳定性。

1 模型引入

假设某一地区在时刻t的易感者、潜伏者、已感者3类分别记为 S ( t)、 E ( t)、 Ii( t)( i = 1 ,2,L, n ),设 A 为进入该地区的总人口数，进入该地区的人口都将作为易感者。Korobeinikov所建立的SEI传染病模型如下：

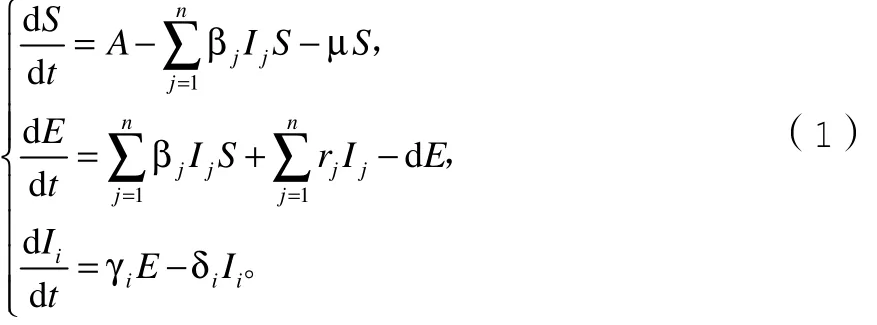
上式中：βjSIj为染病者感染易感者成为潜伏者的双线性发生率，µ为自然死亡率， rj为感染者成为潜伏者的变化率，d为潜伏者的死亡率， γi为潜伏者成为感染者的变化率，δi为感染者的死亡率。

假设参数A、βj、µ、rj、d、γi、δi都是正数，并分别具有实际意义。下面给出分数阶微积分的定义[11]。在本文中采用的是Caputo型的分数阶导数。

定义1：函数 f :R+→R 的α>0阶分数阶Caputo型导数的定义为

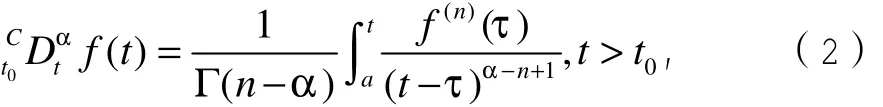
通过Caputo型分数阶的定义，分数阶动力系统的定义为

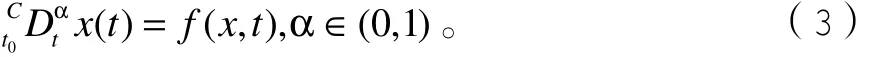
定义2： x0是分数阶系统（3）的平衡点，当且仅当f( x, t0) = 0 。

本文研究的模型如下：

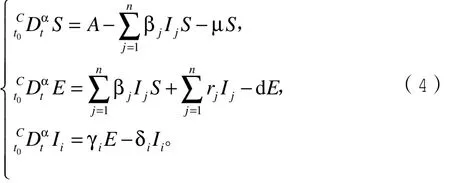
定义基本再生数为

2 平衡点的全局稳定性

下面给出几个关于Caputo型导数的求导公式。

引理1[11]：若C是常数，0α>阶分数阶Caputo

引理2[10]：若()x tR∈是连续可导函数，则对于任意的0tt≥都有

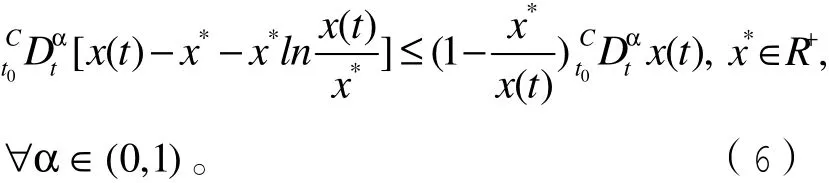
引理3：若()x tR∈是连续可导函数，则对于任意的0tt≥都有

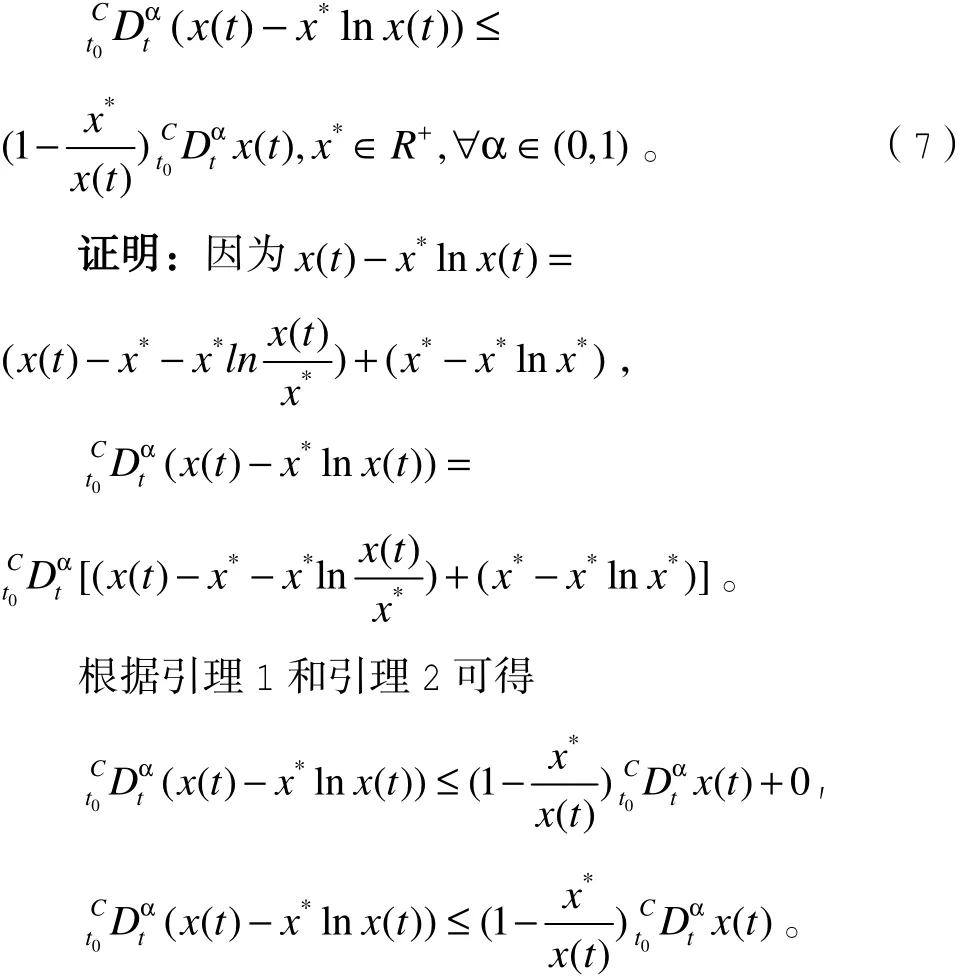
引理1-3将会在对Lyapunov函数的求导中使用。下面给出判断分数阶动力系统平衡点全局稳定性的 2个重要引理。

引理 4[12]（一致渐近稳定性定理）：若 x*是分数阶动力系统x( t) = f( t, x),α ∈ ( 0,1)的平衡点，Ω ∈Rn是一个包含 x*的区域，且 L ( t, x( t) ) :[0,∞)× Ω → R 是连续可微函数，并满足如下条件：

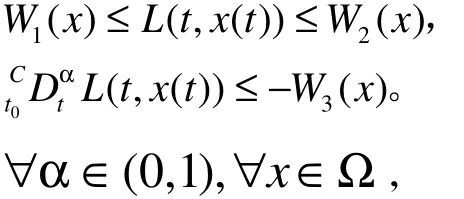
W1( x)、W2( x)、W3( x)是在Ω内的连续正定函数，则系统的稳定点是一致渐近稳定性的。

引理5[2](Lasalle不变原理)：假设D是一个有界闭集,每个x( t) = f( x)的解从D内的一点出发最终仍在D内，如果存在V( x):D→R连续偏导数满足下面条件是E的最大不变集。当t→∞时D中的每个解都将进入M，特别是当 M = { 0},那么t→∞, x → 0 。

定理 1：当 R0<1时，模型（4）存在无病平衡点，无病平衡点在区域内是全局渐进稳定的，即

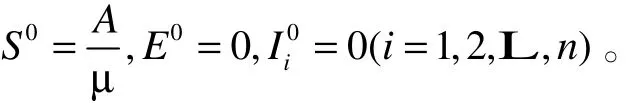
证明：构造如下Lyapunov函数, 其中

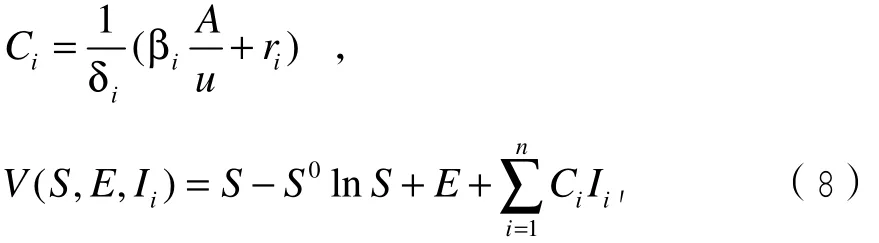
根据引理2对 V ( S, E, Ii) 求导得：

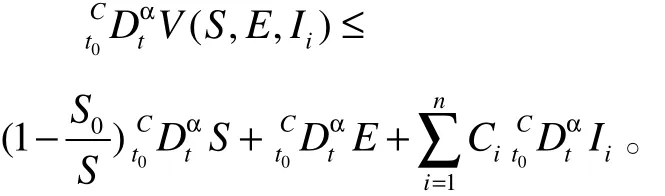
将式（4）中前两式代入得：

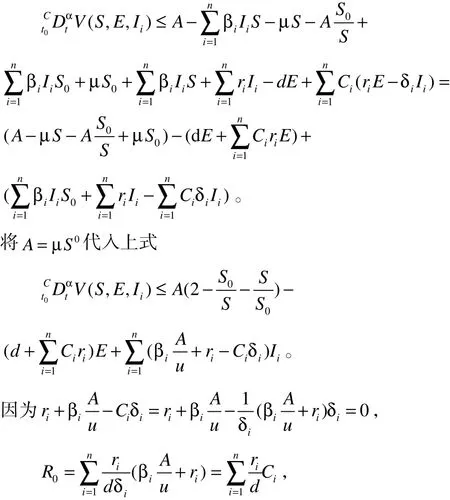
定理2：当 R0> 1 时，模型（4）存在无病平衡点Q0以及地方病平衡点(i = 1 ,2,L ,n )地方病平衡点 Q*在区域内是全局渐进稳定的。

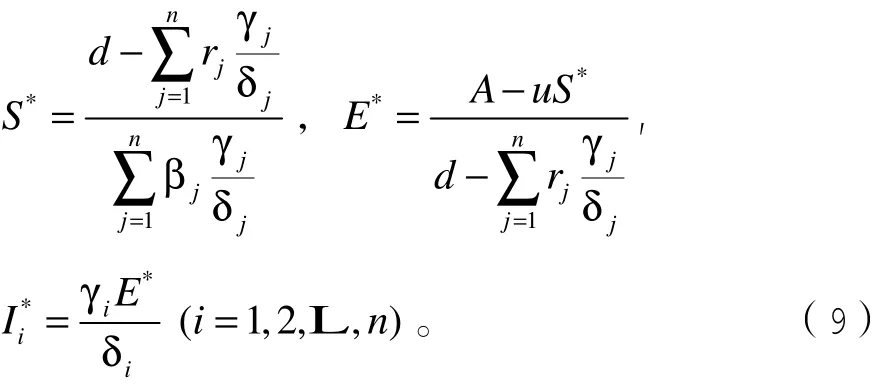
证明: 构造如下Lyapunov函数，其中

根据引理2和引理3对 V ( S, E, Ii)求导得：

3 结论

本文在整数阶SEI流行病模型的研究基础上，将其推广到分数阶模型的情况，研究了一类具有标准发生率分数阶SEI流行病模型，并构造相应的Lyapunov函数判断平衡点的全局稳定性，得出以下结论：

（1）当 R0<1时，模型只存在无病平衡点 Q0，无病平衡点 Q0在区域内是全局渐进稳定的，疾病最终会在该地区最终灭绝不会流行。

（2）当 R0> 1 时，模型存在无病平衡点 Q0以及地方病平衡点 Q*，地方病平衡点 Q*在区域内是全局渐进稳定的。