线性代数中的二次型应用
刘媛媛
(陇南师范高等专科学校 初等教育学院,甘肃 陇南 742500)
从代数学的观点看,化标准型过程就是将变量的线性变化化简成一个二次齐次多项式,使它只含有平方项.这样一个问题,在实际问题中会经常遇到,下面介绍它的基本性质.
在解析几何中,我们看到,中心是原点的二次有心曲线方程是
ax2+bxy+cy2=d.
可把二次有心曲线方程化为只含有平方项的标准形式a′x′2+c′y′2=d,从平方项的标准形式,我们很容易判断曲线的类型,进而可以研究曲线的性质.
基于上面的结果,我们试想能否把空间解析几何中的二次曲面方程
也化为只含有平方项的标准形式,进而来研究曲面的性质.
二次曲线ax2+bxy+cy2=d的左边是一个二次齐次多项式,化标准型过程就是通过变量的线性变换为二次齐次多项式,即只含有平方项的标准形式[1].
一般地,F是一个数域,F中n个变量x1,x2,…,xn的二次型表达式为
1 用代数方法求椭圆(球)面(体)积
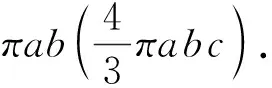
任意给出一个二元不等式
ax2+2b1xy+cy2+2d1x+2e1y≤h,
(1)
当h>0时,可以化为
ax2+2bxy+cy2+2dx+2ey≤1 ,
(2)
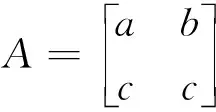
2 二次型在二维求解平面图形中的应用
以二次曲线的主直径为新坐标轴,化简方程4x2-4xy+y2+6x-8y+3 =0,写出相应的坐标变换公式.下面我们来详解.
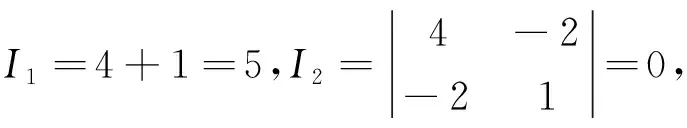
故曲线为无心曲线,特征方程为λ2-5λ=0,解之得λ1=5,λ2=0.
由λ1确定的非渐近主方向为x1y1=-21, 由λ2确定的渐近主方向为x2y2=12.
由于F1(x,y)=4x-2y+3,F2(x,y)=-2x+y-4,则λ1确定的唯一主直径为2x-y+2=0,将它取为O′x′轴,由
2x-y+2=0,4x2-4xy+y2+6x-8y+3=0 ,
从而有正变换公式[3]
代入原方程并整理得
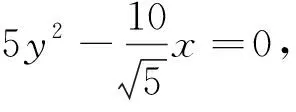
同时
3 二次型在三维求解立体图形中的应用
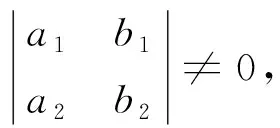
解:因为a1a2+b1b2=0,所以直线a1x+b1y+c1=0与a2x+b2y+c2=0互相垂直,分别取为oy轴与ox轴,得坐标变换公式为
其中,ai,bi(i=1,2)不全为零[4].
式中正负号的选取使得第一式中x的系数与第二式中y的系数相同,代入原方程得
由
a1a2+b1b2=0,

则
a1=γb2,b1=-γa2,


代入得
γ2x′2+y′2=1,
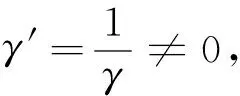
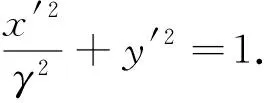
——如何培养学生的创新思维

