MR阻尼器-网格结构的滑模变结构控制

雷海涛，李志军，刘园园

(西安工业大学 建筑工程学院，西安 710021)

空间网格结构具有自重轻、透明度高和坚实性好等特点被广泛应用于大型公共建筑中.但是由于整体阻尼小、频率分布集中以及杆件刚性大等原因，当遭受大风、地震等恶劣外部环境时，空间网格结构震动幅度大，往往不能达到常规的抗震性能[1-3].

磁流变阻尼器(简称MR阻尼器)能够依据环境变化而迅速调整结构的瞬时动力参数，是较为先进的可控构件，在响应速度、耗能、调节范围等方面具有明显的优势，此外，它的体积小、构造简单、可提供的阻尼力较大、兼容性良好，尤其在结构减震方面具有明显优势[4-5].文献[6] 以一个10层钢筋混凝土框架结构为例，建立了磁流变阻尼器受控框架结构的空间杆系计算模型，采用LQR算法计算受控结构所需的最优控制力.文献[7-8]将新型压电摩擦阻尼器进行优化后布置于空间网格结构中,利用基于传统LQR主动控制算法的半主动控制策略对该结构在地震动作用下的动力响应进行了分析，结果表明了新型控制装置和控制策略的有效性.但是传统LQR控制算法由于需要结构系统精确的模型参数，所以存在鲁棒性相对较差的问题.滑模变结构控制(Sliding Mode Control，SMC)由于不需要结构系统精确的参数模型，具有算法简单、鲁棒性能好和可靠性高的特点，使得其在复杂系统中存在不确定或者不精确参数的情况下，往往可以取得良好的控制效果.文献[9]率先将变结构控制应用到土木工程结构振动控制领域.文献[10-11]基于指数趋近律方法设计了控制律，并将其应用于连续系统、离散系统和时滞系统模型，结果表明所提出的变结构控制方法显著减小了结构在地震作用下的地震峰值响应，对结构模型参数的不确定性具有较好的鲁棒性.文献[12-13]等基于RBF神经网络的特点，提出了一种基于RBF神经网络调节控制增益的结构滑模控制算法，较好地解决了控制系统过大抖振的问题.

为了探究装有磁流变阻尼器的网壳结构在地震动的作用下结构鲁棒控制策略，本文引入指数趋近律的思路，制定出滑模控制方法，并提出相应的半主动控制策略.以凯威特型单层网格结构模型为例，通过对比未控和受控状态下结构位移及加速度峰值响应，进行仿真试验验证选用的半主动控制系统的有效性.

1 运动方程

1.1 磁流变阻尼器的力学计算模型

据文献[14]的研究，MR阻尼器的力-位移关系式表示为

(1)

式中：L为活塞有效长度；Ap为活塞的有效面积；Dh为活塞中的阻尼孔直径；D为缸体内径.

据此式可知，所求解的阻尼力F包括两项，其一是粘滞阻尼力,他依赖于流体自身的动力粘度，不可变动；其二是库仑阻尼力，和MR的屈服强度相关.在执行过程中，调整电流大小，继而调控τy值，实现对阻尼力F(t)的最终控制.通过推导可以得出剪切屈服应力τy和电流I之间的关系为

τy=A1e-1+A2ln(I+e)+A3I

(2)

1.2 建立系统空间状态模型

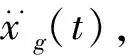
(3)

X(t)=[x1(t),x2(t),…,xn(t)]T分别为n维加速度、速度、位移向量；M、C、K分别为(n×n)维质量、阻尼、刚度矩阵；I为n维单位列向量，E为(n×m)维控制装置位置矩阵，U(t)为(m×1)维MR阻尼器的控制力向量.

(4)

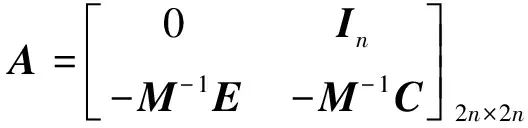
其中In为n×n维单位矩阵.

2 滑模控制算法的半主动控制

滑模变结构控制是一种非线性控制，准确的说就是迫使系统在特定的情况下，沿着轨迹进行高频率但是幅度较小的振动.且系统的参数及系统的扰动，对于滑动模态的设计没有影响.

2.1 运动方程及其简约型

为简化结构的运动方程，令式(4)中

(5)

由式(5)两边对时间求导可得：

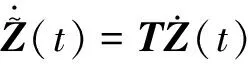
(6)

将式(4)代入式(6)可得：

(7)

(8)

则上式可表达为

(9)

(10)

2.2 切换函数的确定

设滑模面[15]具有如下形式：

(11)

其中Z∈R2n,U∈Rm,S∈Rm.

确定滑模面的方法有很多，如极点配置法、二次型最优配置法等，具体见文献[14-15].

2.3 滑模控制器的设计

滑模运动实质上是由滑模运动及趋近运动两种类型综合而成的，依照滑模变结构的设计，必须满足可达性条件，可是并未对切换面的表达形式做出明确规定，基于此，本文采用指数函数的趋近律[15]，表达式为

(12)

式中：sgn为符号函数；δ=diag[δ1,δ2,…,δm]和ε=diag[ε1,ε2,…,εm]为m维正对角矩阵，设置好合适的δi及εi值，不仅可以削弱系统抖振，还可以促进趋近运动的有效进行.

按照式(13)进行求导，有

(13)

则可以得出基于指数趋近律的控制律

δsgn[S(t)]+εS(t)

(14)

2.4 半主动控制算法

由分析可得，输出阻尼力的大小是由磁流变阻尼器自身设计参数，还有结构运动状态的影响所决定的，实际输出控制力是不会超过阻尼器最大极限控制力的.对于建筑结构振动问题来说，由上式(14)求得的力并非实际控制力，因此无法适用于实际应用的MR变阻尼器.依据此，为了求解实际控制力，便引入饱和控制方法，具体公式如下：

(15)

3 算 例

选定近年来应用较多的凯威特型单层网格结构作为本文实验模型[2]，该结构中径向2格，环向6格，内环半径408 mm，底层圆半径800 mm，底层高120 mm，第二层高40 mm，一共有13个节点，以实心钢球作为结构材质，单体质量为1.5 kg，杆件均为壁厚1 mm、直径∅8 mm的合金空心管，支座是三向不动铰支座.为了得到动力学方程的系数矩阵K、M、C，这里利用有限元ANSYS对桁架桥梁结构进行建模.其模型如图1所示，并标出了网格结构的节点编号及杆单元编号.

3.1 磁流变阻尼器的布置

在已建立的模型中采用地震响应谱来对结构进行地震模态分析.结果显示，在X方向上节点2和节点5的位移变化最大，在Y方向上节点3、节点4、节点6、节点7的位移变化最大；杆28、杆29、杆34、杆35的X与Y的位移都比较大.为减小系统的成本及控制的复杂性，通过优化比较后在模型上放置三个MR阻尼器作为结构的减震装置，对结构进行半主动控制分析，阻尼器分别放置在14杆、28杆、33杆上.放置示意图如图2所示，MR阻尼器设计参数具体参考文献[14].

3.2 仿真分析

考虑到该工程架构严格对称，只需具体探究节点1，2，3和7的工况，具体对比情况及控制效果示意如下.为了能够更为直观的看出MR阻尼器结合半主动控制策略对于结构减震的作用，因此定义：

β=(X无-X有)/X无×100%

(16)

图1 网格结构ANSYS模型图

式中:X有为结构在受控状态下结构位移及加速度的峰值响应;X无为结构在未控状态下结构位移及加速度的峰值响应.本文选用El Centro波记录和南京地震波记录，采样周期为0.02 s，沿X方向输入.

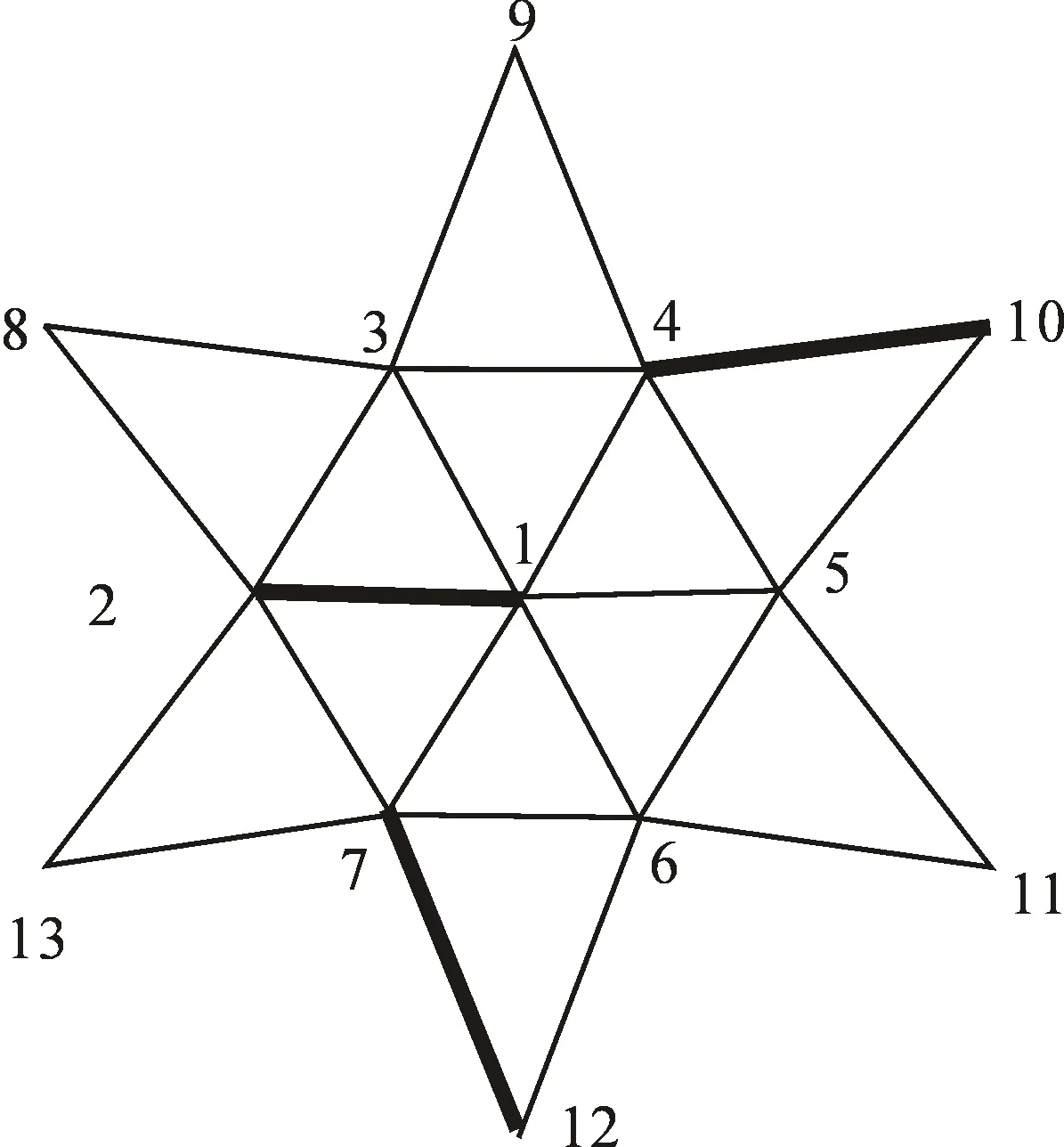
图2 磁流变阻尼器布置

3.2.1 El Centro 波作用下的结构反应

图3和图4是在El Centro波作用下采用基于指数趋近律的滑模变结构控制方法与未控时结构1，2，3和7节点的位移和加速度的时程对比曲线.从图中可以看出，结构在受控状态下的响应要明显小于结构在未控状态下的响应.结构1，2，3和7节点的位移及加速度的峰值见表1.

图3 El Centro波作用下节点位移时程对比曲线

图4 El Centro波作用下节点加速度程时对比曲线

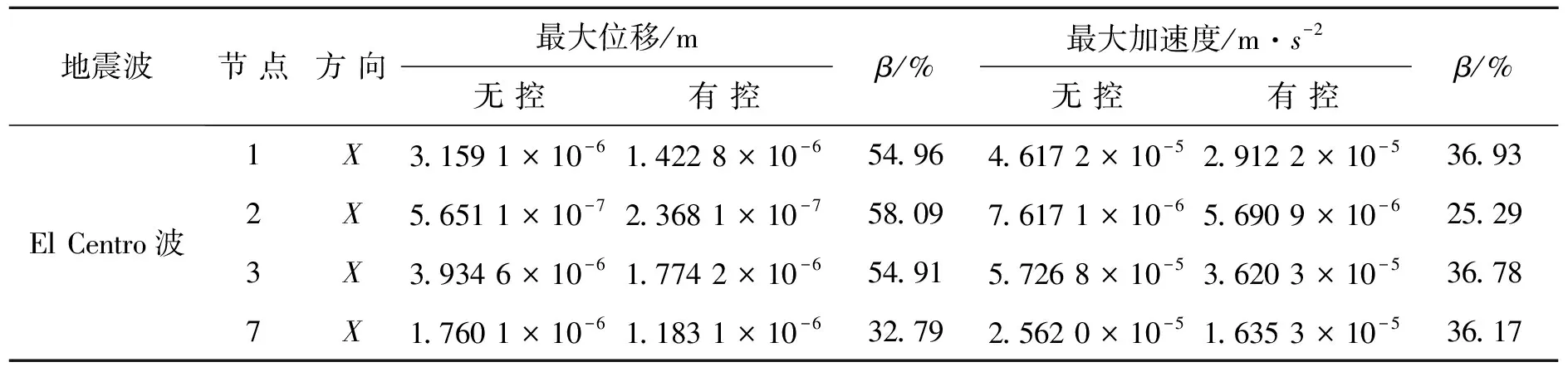
表1 El Centro波作用下节点位移响应与加速度响应

从表1中可以看出该控制方法有效地减小了各节点位移及加速度的峰值，最大降幅达58.09%，控制效果明显.

3.2.2 南京波作用下的结构反应

图5和图6是在南京波作用下结构1，2，3和7节点在未控和受控状态下位移和加速度的时程对比曲线.从图中可以看出，结构在受控状态下的响应要明显小于未控状态下的响应.表2为结构1，2，3和7节点位移及加速度的峰值，从表中可以看出该控制方法有效地减小了各节点位移及加速度的峰值，最大降幅达53.55%，依然具有明显的控制效果.

图7和8为结构节点3和节点7的控制力时程曲线图，从图7～8可以看出，网格结构并未产生过大的抖振，说明基于滑模控制算法的半主动控制方法的具有较好的可靠性.

根据磁流变阻尼器的力学计算模型，由式(1)与式(2)可得阻尼器所需的外部输入电流及控制力.由于计算公式较为复杂，因此只给出了3节点和7节点的计算结果.表3所示为两种地震波作用下，结构中节点3和节点7的最大控制力及外部输入的电流大小，以方便控制网格结构的振动，增加了结构的安全性及稳定性.

3.2.3 滑模控制算法鲁棒性的验证

为了验证本文所提算法的鲁棒性能，通过下调20%的模型刚度再次进行时程分析，试验结果见表4.从表4中可以得出，结构的节点在未控状态下的加速度及位移的峰值都要明显大于结构在受控状态下的峰值，由此可以说明当结构的刚度变为原结构刚度的80%时，本文所采用滑模控制算法的半主动控制对结构依然具有较好的控制效果，结构在地震作用下并没有出现失稳现象，从而验证了该算法具有较好的鲁棒性.

图5 南京波作用下节点位移程时对比曲线

图6 南京波作用下节点加速度程时对比曲线

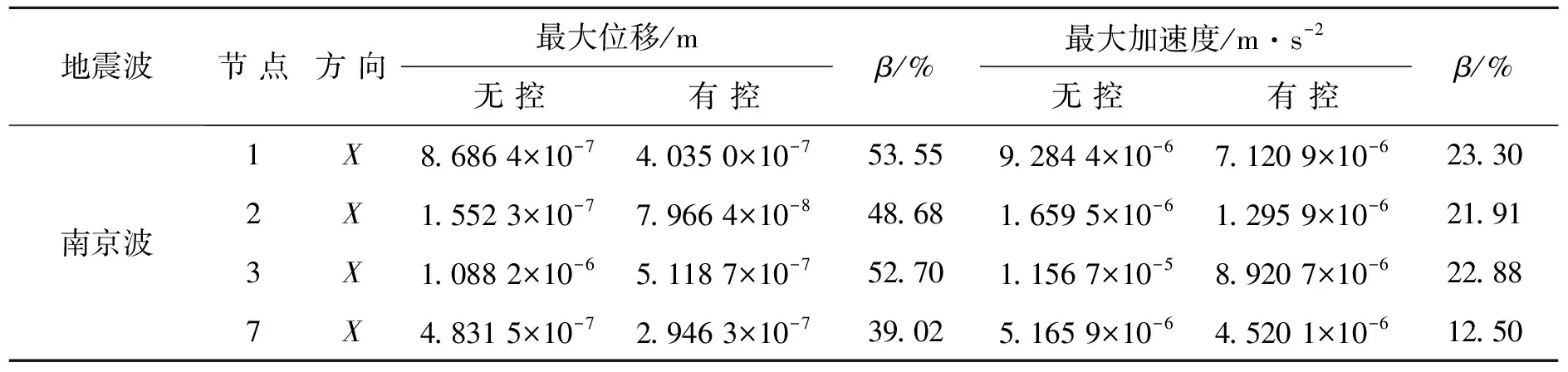
表2 南京波作用下节点位移响应与加速度响应

图7 El Centro波和南京波作用下节点3控制力时程曲线

表4 刚度下调后节点位移响应与加速度响应

4 结 论

1) 本文引入磁流变阻尼器作为网格结构的控制装置，采用基于指数趋近律的滑模控制算法，结合半主动控制策略，对网格结构进行了半主动控制分析研究.

2) 以凯威特型单层网格结构为例，采用El Centro波和南京波完成了仿真试验.试验结果表明，结构在受控状态下的位移及加速度响应明显小于未控状态下的响应，并且有效地减小了结构的地震峰值响应.通过节点3和节点7的控制力时程曲线可以看出结构并未产生过大的抖振.将原结构刚度下降20%后再次进行时程分析发现结构并未出现失稳现象，从而验证了该方法具有较好的控制效果和鲁棒性.

3) 本文选取的结构模型较简单，考虑实际空间网格结构的复杂性，该方法对复杂空间网格结构的控制效果需要作进一步的研究.