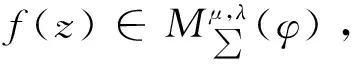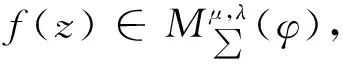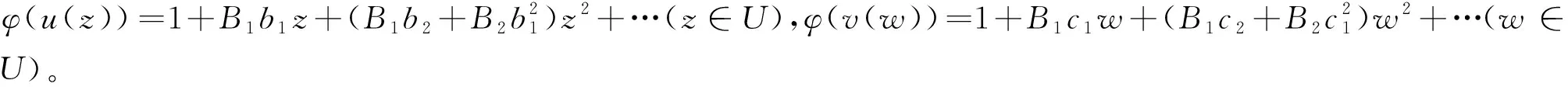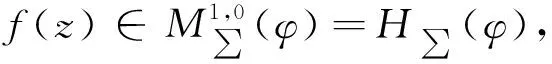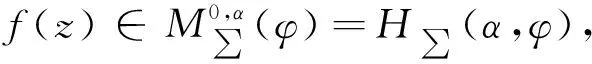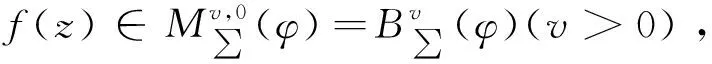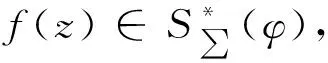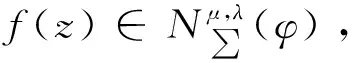几类双单叶函数类的系数估计
郭 栋, 李宗涛
(1.滁州职业技术学院 基础部,安徽 滁州 239000;2.广州民航职业技术学院 基础部,广东 广州 510403)
引 言
令H表示在单位圆U={z:|z|<1}内具有下述形式的解析函数类
(1)
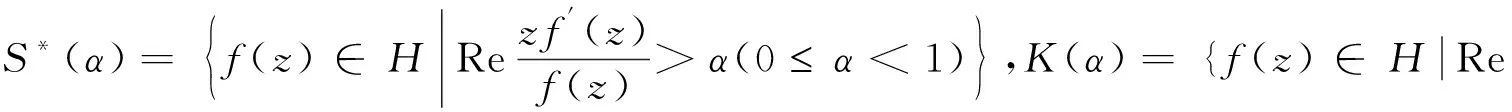
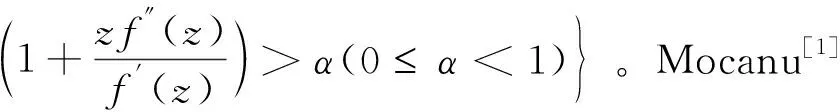
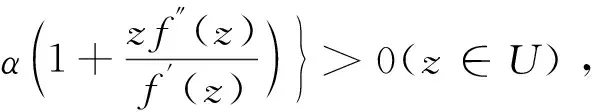
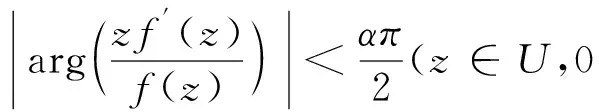
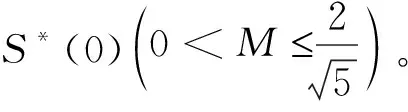
Ma[5]介绍了更一般化的函数类S*(φ),K(φ),满足下式:
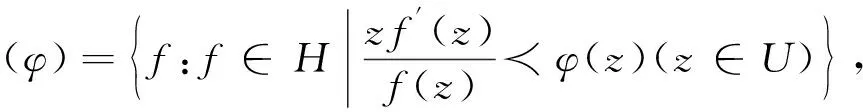
其中φ(z)=1+B1z+B2z2+B3z3+…(Bn∈R,B1>0),φ(z)是U内解析的正实部函数且满足φ(0)=1,φ′(0)>0。
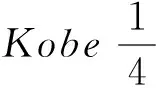
f-1(f(z))=z(z∈U),
这里
(2)
函数f(z)∈H在U内称为双单叶函数当且仅当f(z)和f-1(w)在U内都是单叶函数。现记∑表示单位圆U内所有具有(1)式的双单叶函数。M.Lewin[6]首先引入了双单叶函数族,证明了f(z)∈∑,则|a2|1.51。随后许多作者研究了双单叶函数族子类|a2|、|a3|的上界问题(文献7-11)。
Guo[12]定义了函数类M(α,λ,ρ),若f(z)∈H满足
其中α≥0,λ≥0,0ρ<1,则称函数类f(z)∈M(α,λ,ρ)。令α=0,λ=α∈R,ρ=0,则有此函数类称为α-凸函数。
定义1令μ≥0,λ则称如果f(z)满足
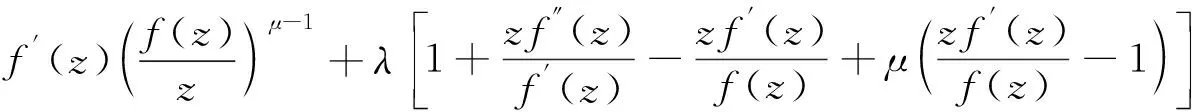
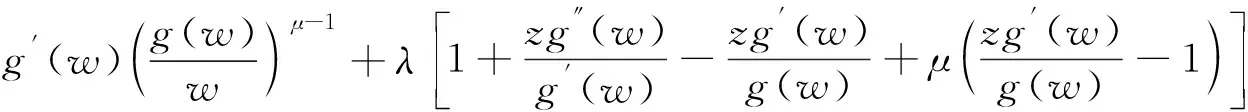
其中g(w)=f-1(w)。
定义2令μ≥0,λ≥0,0 其中g(w)=f-1(w)。 其中g(w)=f-1(w)。 定义4令λ≥1,μ≥0,0 其中g(w)=f-1(w)。 在定义1、3中,令参数取一些特殊值就得到我们熟知的双单叶函数类。例如: 本文的主要工作是利用分析的技巧讨论了上述四类函数类的前两项系数估计,所得结果推广了一些作者的相关结论。 为了得到本文的结果需要以下引理。 引理[13]设ω(z)=d1z+d2z2+d3z3+…在U内解析且满足|ω(z)||z|,则有 |d1|1, |d2|1-|d1|2。 |a2| (3) |a3| (4) (5) (6) 将f(z)、g(w)的幂级数展开式代入(5)、(6)式,比较z和z2的系数及w和w2的系数,得 (1+λ)(1+μ)a2=B1b1, (7) (8) -(1+λ)(1+μ)a2=B1c1, (9) (10) 由(7)和(9)式可得 b1=-c1, (11) (12) 由(8)和(10)式可得 (13) 将(11)和(12)式代入(13)式,化简得 (14) 由(11),(12)和(14)式可得 (15) 利用引理及(15)式,可得 所以 |a2| (16) 由(11),(8)和(10)式,可得 (17) 利用引理,由(16),(17)和(7)式,可得 |a3| 所以 |a3| 定理得证。 在定理1中,令μ=1,λ=0得下面推论。 |a3| 注释:推论1就是文献[2]中定理2.1。 在定理1中,令μ=0,λ=α得下面推论。 |a3| 注释:推论2比文献[2]中定理2.3的估计更精确。 在定理1中,令μ=v,λ=0得 |a2| |a3| 注释:推论3比文献[10]中定理2.1的估计更精确。 在定理1中,令μ=0,λ=0得 |a3| 在推论2中,令α=1得 推论5如果f(z)∈M∑(1,φ),则有|a2|和 |a3| 定理2假设f(z)∈M∑(μ,λ,k),则有 |a2| (18) |a3| (19) 证明:因为f(z)∈M∑(μ,λ,k),则存在u(z)=b1z+b2z2+b3z3+…,v(w)=c1w+c2w2+c3w3+…满足 (20) (21) 将f(z)、g(w)的幂级数展开式代入(20)、(21)式,比较z和z2的系数及w和w2的系数,得 (1+λ)(1+μ)a2=-kb1, (22) (23) (1+λ)(1+μ)a2=kc1, (24) (25) 由(22)和(24)式得 b1=-c1, (26) (27) 用(23)加上(25)式,可得 (28) 利用引理及(28)和(22)式,可得 (1+μ)(2λ+μ+2)|a2|2k(|b2|+|c2|) 所以 |a2| (29) 用(23)式减去(25)式,可得 (30) 利用引理,由(22),(26),(29)和(30)式,可得 |a3| 推论6如果f(z)∈M∑(μ,0,k),则有|a2|和 |a3| 在推论6中,令μ=0,k=1得 推论7如果f(z)∈M∑(0,0,1),则有|a2|和|a3| 在推论6中,令μ=1,k=1得 推论8如果f(z)∈M∑(1,0,1),则有|a2|和|a3| 推论9如果f(z)∈M∑(0,α,k),则有|a2|和 |a3| 在推论9中,令α=1,k=1得 推论10如果f(z)∈M∑(0,1,1),则有|a2|和|a3| 类似于定理1的证明,有 |a2| |a3| 在定理3中,令μ=1得 |a2| |a3| 注释:此推论就是文献[7]中定理2.5。 类似于定理2的证明,有 定理4假设f(z)∈N∑(μ,λ,k),则有|a2|和 |a3| 推论12假设f(z)∈N∑(1,λ,k),则有|a2|和 |a3| 在推论12中,令λ=0,k=1得 推论13假设f(z)∈N∑(1,0,1),则有|a2|和|a3|1。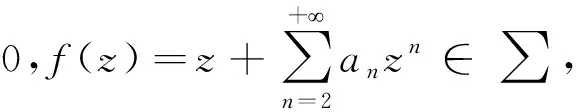
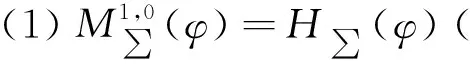
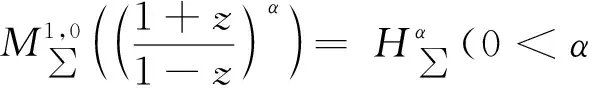
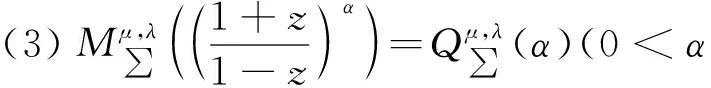
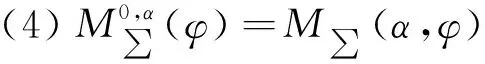
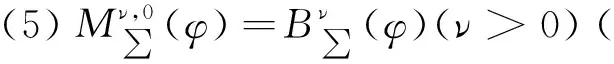
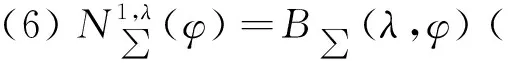
1 预备知识
2 主要结果及证明