基于公平度和惩罚函数的OFDMA自适应资源分配

袁建国, 张 芳, 王竟鑫, 王 永, 林金朝, 庞 宇

(1. 重庆邮电大学光电信息感测与传输技术重庆市重点实验室, 重庆 400065; 2. 重庆邮电大学光通信与网络重点实验室, 重庆 400065)

0 引 言

正交频分多址(orthogonal frequency division multiple access, OFDMA)技术[1-3]可以利用各个子信道的信道信息将不同的频带资源动态地分配给不同的用户来实现多址接入,并以此提高系统资源的综合利用率。而正交频分复用(orthogonal frequency division multiplexing, OFDM)技术[4-5]作为OFDMA的一种调制方式,其子信道在时间上正交、在频率上相互重叠,这样不仅能够有效地提高频谱利用率,同时也能提高数据传输速率[6]。保护间隔和循环前缀的使用,可有效地对抗多径效应带来的码间干扰和子信道间干扰等问题。鉴于此,OFDM技术的种种特性都为研究OFDMA自适应资源分配提供了便利的条件。

OFDMA自适应资源分配的研究主要基于速率自适应(rate adaptive, RA)准则[7-9]和边缘自适应(margin adaptive, MA)准则[10-11]。迄今为止,众多文献对基于RA准则的OFDMA自适应资源分配中系统容量和用户公平度的问题给出了相应的解决办法[12-16]。文献[12]提出的Shen算法在实现系统容量最大化的同时也保证了用户的速率比例约束,该算法几乎可以实现严格意义上的公平。但是,该文算法为了满足用户间的公平度对系统容量没有较大的提升。文献[13]提出了一种联合子载波分配与功率分配的算法,该算法虽然能实现自适应的资源分配,但是该文算法忽略了速率需求最小用户的公平度。文献[14]提出了一种在保证用户公平的同时将子载波进行分组的资源分配方案。虽然该算法可以实现最大化的系统容量,但是该算法的子载波分配部分只是考虑到了用户的公平度,并未充分考虑系统容量。文献[15]的Jang算法证明了单用户下等功率分配方式和注水算法所得到的系统容量几乎一样。该文算法可以实现最优的系统容量,但却没有考虑用户的公平度。文献[16]提出了一种基于鱼群算法的资源分配方案。该文算法可以实现较高的系统容量,同时也能兼顾用户的公平度。但是该文算法不能够根据用户的需求对系统容量和用户公平度进行灵活的调整,同时该文的子载波分配算法为了提升系统容量而牺牲了部分用户的公平度。

本文在研究上述文献的基础上,为了进一步解决基于RA准则的OFDMA自适应资源分配中系统容量和用户公平度的问题,提出了一种基于公平度和惩罚函数的OFDMA自适应资源分配算法。在本文算法的子载波分配中,为了最大化系统容量并兼顾用户的公平度,子载波根据给定的公平度约束实现合理的分配。但是在子载波分配完成后并不能较好地兼顾系统容量和用户公平度,所以在本文算法的功率分配中,基于惩罚函数设计了一种新的适应度函数,作为基于模拟退火(simulated annealing,SA)思想的改进人工蜂群(artificial bee colony, ABC)算法的寻优适应度。仿真结果表明本文算法不仅可以实现较高的系统容量,而且还可以满足给定的公平度约束。

1 系统模型

OFDMA自适应系统的模型如图1所示。

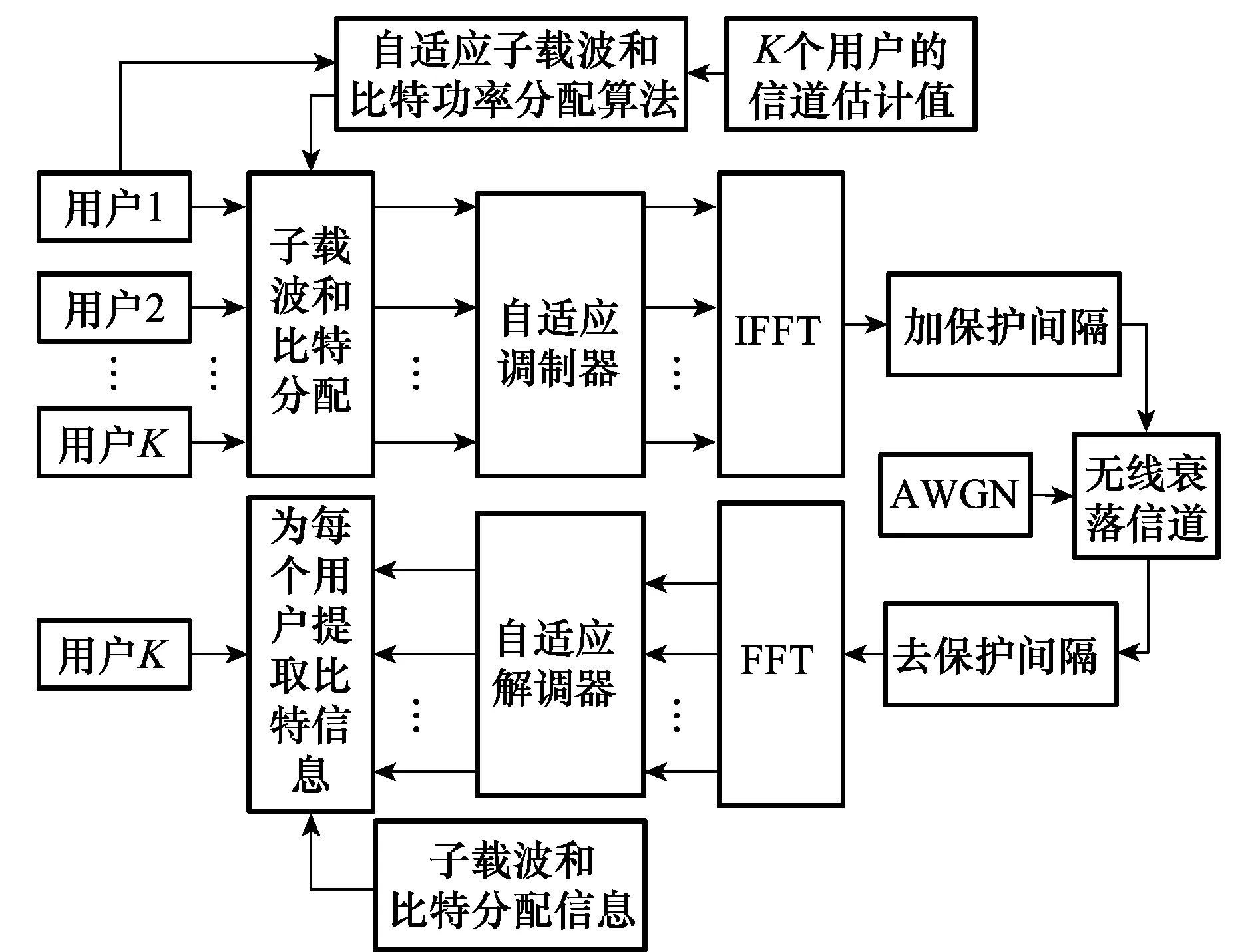
图1 OFDMA自适应系统的模型图Fig.1 Model of OFDMA adaptive system

在OFDMA自适应系统中,通过对K个用户的信道进行信道条件的估计,基站可以获取这K个用户的实时信道状况。然后基站根据这K个用户的实时信道条件,利用自适应子载波和比特功率分配算法对各个子信道设置不同的调制参数,以对K个用户数据进行不同程度的调制。之后,基站端便将这K个用户的数据通过无线衰落信道发送到移动台端。而移动台端利用基站同时发送过来的子载波和比特分配信息,对数据进行相应的解调后便得到其有用的数据。

根据图1所示,假设OFDMA系统中有N个子载波和K个用户,并且N0为加性高斯白噪声(additive gaussian white noise, AGWN)的功率谱密度,无线衰落信道的带宽为B,总发射限制功率为Ptotal,第k个用户在其第n个子载波上的信道响应和分配功率分别为hk,n和pk,n,子载波分配矩阵元素为ck,n。根据RA准则,带有公平约束的OFDMA自适应系统优化模型可以表示为

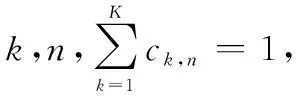
(c)R1:R2:…:RK=λ1:λ2:…:λK

(1)

式中,约束条件(a)表示若子载波n被分配给用户k,则ck,n=1,否则ck,n=0。并且,同一个子载波仅且只能被某一个用户使用。约束条件(b)表示每个子载波所分配的功率值必须大于等于0,并且分配给所有子载波的功率和不得超过总发射限制功率Ptotal。为了保证系统中各个用户的公平度,在约束条件(c)中预设了用户之间的速率约束R1:R2:…:RK=λ1:λ2:…:λK。约束条件(c)中,Rk表示第k个用户期望的速率值,Rk可以表示为

(2)

式中,Nk表示分配给第k个用户的子载波数目;bk,n表示第k个用户在其第n个子载波上分配的比特数量,即

(3)

2 基于公平度的子载波分配算法

2.1 子载波分配算法的优化模型

(4)

那么,利用式(4)对式(1)中的约束条件(c)进行变形,并考虑到系统容量和用户公平度,设置一个公平度约束值ξ,最后可以得到新优化模型:

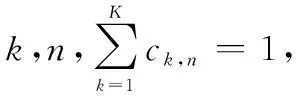
(c) Fairness≥ξ

(5)

分析新的优化模型可知,式(1)的约束条件(c)被公平度函数Fairness和公平度约束值ξ代替,并且通过调节公平度约束值ξ的大小,即可兼顾系统容量和用户公平度。

2.2 子载波分配算法

文献[12]中的子载波分配算法首先依次为每个用户分配一个最好的子载波,当还有剩余子载波时,优先对最小速率比例的用户分配子载波,直到子载波分配完毕。该算法的优点是充分考虑到了最小速率比例用户的需求,从而保证了用户的公平度。但是,该算法对系统容量的提升并不明显。而文献[16]中所提及的子载波分配算法首先确定每个用户需要的子载波数,然后优先对最小速率比例的用户分配子载波,最后分配剩余的子载波。该子载波分配算法在执行过程中可以较好地提升系统容量,但是该算法在分配剩余子载波的过程中降低了用户的公平度。

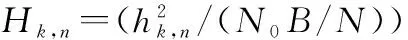
步骤1设Rk=0,ck,n=0,其中,k=1,2,…,K；n=1,2,…,N,并且A={1,2,…,N}。

步骤2a) 设U={1,2,…,K},则在任意用户∀i∈U和任意子载波∀m∈A中,找到一个用户k和一个子载波n,使其满足Hk,n≥Hi,m,然后利用找到的Hk,n更新ck,n=1,U=U-{k},A=A-{n}和Rk=Rk+bk,n;

b) 重复步骤a),直到U=∅。

步骤3当A≠∅时,设Y={1,2,…,K},然后根据式(4)计算公平度函数Fairness的值并比较Fairness和公平度的要求值ξ的大小。

步骤3.1若Fairness≥ξ

a) 在任意用户∀v∈Y和任意子载波∀z∈A中,找到一个用户k和一个子载波n,使其满足Hk,n≥Hv,z;

b) 根据找到的Hk,n更新ck,n=1,Rk=Rk+bk,n和A=A-{n}。

步骤3.2若Fairness<ξ

a) 找到用户k,k=argmink∈YRk/λk;

b) 在用户k下,找到子载波n,对任意的子载波∀u∈A,Hk,n≥Hk,u;

c) 根据找到的Hk,n更新ck,n=1,Rk=Rk+bk,n和A=A-{n}。

上述算法的步骤2只为每个用户分配一个相对最好的子载波以提高系统容量。在步骤3中,当满足公平度约束值ξ时,就为用户分配相对最好的子载波以提高系统容量;否则,就根据用户的速率比例Rk/λk提升用户之间的公平度。

本节的子载波分配算法虽然可以实现较大的系统容量,但是并不能够保证用户的公平度就能满足给定的公平度约束ξ。因而,本文还通过功率分配的研究来进一步平衡系统容量和用户公平度。

3 基于惩罚函数的功率分配算法

3.1 功率分配算法的优化模型

在子载波分配完成后,系统的优化模型由式(5)变为

(b) Fairness≥ξ

(6)

式(6)的优化模型是非线性的,而群体智能优化算法[17-19]一般不要求目标函数和其约束条件的连续性和凸性,这为解决非线性优化问题提供了便利的途径。ABC算法作为群体元启发式智能优化算法,具有结构简单、可调参数少、鲁棒性强、稳健性高等优点。而SA算法具有局部寻优能力强的特性,可以跳出局部极值进行全局寻优。所以,针对系统的优化模型(6),本文采用基于SA思想的ABC算法来解决式(6)的非线性优化问题。

3.2 ABC算法和SA算法的介绍

3.2.1 ABC算法简介

ABC算法[20]是受蜜蜂觅食行为的启发而得到的一种优化算法。在ABC算法中的蜜蜂分为3种:引领蜂、跟随蜂和侦查蜂,其中引领蜂和跟随蜂进行对蜜源的开采,并且每一蜜源和每一引领蜂一一对应,侦查蜂对蜜源进行发掘以避免蜜源种类过少。基本的ABC算法主要包括引领蜂时期、跟随蜂时期和侦察蜂时期,相应的搜索过程如下:

步骤1初始化蜜源:侦查蜂在可行域内搜索2SN个蜜源(可行解),选择较优的SN个蜜源作为初始标记蜜源,然后从中选出一个最优的蜜源(最优解)。

步骤2引领蜂时期:引领蜂发现这SN个初始标记蜜源后,便不断地通过式(7)寻找新的蜜源并比较不同蜜源的花蜜量(优化问题的适应度值),同时贪婪选择较优的蜜源更新已标记的蜜源,进而招募跟随蜂。

Vij=xij+R(xij-xkj)

(7)

式中,j表示维数且j∈{1,2,…,D}(D为搜索空间的维度);R∈(-1,1),决定扰动幅度;xij表示蜜源i在第j维的原位置;Vij表示蜜源i在第j维上的新位置;k∈{1,2,…,SN}且k≠i,用来提供搜索方向。

步骤3跟随蜂时期:跟随蜂利用引领蜂传递的信息,以轮盘赌的方式按式(8)轮盘选择合适的蜜源,并在选择的蜜源附近按式(7)进行邻域搜索,寻找新的蜜源并比较优劣,最后选择较优的蜜源更新本次循环所标记的蜜源

(8)

步骤4侦察蜂时期:当引领蜂在采蜜的过程中,某个蜜源经过数次的开采后没有发生变化,那么相应的引领蜂放弃该蜜源转变为侦查蜂,同时随机搜索新的蜜源来取代该原蜜源,最后更新本次循环的最终标记蜜源和最优蜜源。

步骤5若不满足终止条件,则转到步骤2。

3.2.2 SA算法简介

SA算法[21]将固体的内能模拟为目标函数f(X),用温度T作为控制参数进行全局搜索运算。SA算法允许目标函数f(X)以一定的概率P接受比当前解还要差的解,这样就有可能使算法跳出局部极值,达到全局寻优的效果。基本的SA算法的步骤如下:

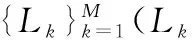
步骤2当T=Tk时,执行Lk次的下列搜索过程:

步骤2.1在当前解Xk的邻域中随机扰动产生新解Xk*,并计算其目标函数值f(Xk*);

步骤2.2计算Δ=f(Xk*)-f(Xk),若Δ≥0,则令Xk*为当前解;否则,计算在当前解和温度下接受新解的概率P=exp[(f(Xk*)-f(Xk))/Tk];

步骤2.3在区间(0, 1)上产生一个随机数φ。如果P>φ,则Xk=Xk*,f(Xk)=f(Xk*);否则当前解和目标函数值不发生变化;

步骤2.4若上述搜索过程执行了Lk次,则判断是否满足终止条件S,若满足终止条件,则输出最优解,算法结束;否则转到步骤3;

步骤3对当前温度参数Tk降温并产生新的温度控制参数Tk+1和Mapkob链长Lk+1,转到步骤2。

3.3 功率分配算法

虽然ABC算法具有良好的全局寻优能力,适合求解带约束的非线性优化问题,但是从仿真中也可以看出其难免会陷入局部最优和搜索停滞的状况。而SA算法恰恰具有跳出局部极值进行全局搜索的能力,同时也避免了搜索停滞的现象。所以本文提出了一种基于SA思想的改进ABC算法,以下简称SA-ABC算法。

由于实际的无线通信系统中,子载波数N远远大于用户数K。为了降低SA-ABC算法在N个子载波之间进行功率寻优的复杂度,本文利用SA-ABC算法在K个用户之间进行功率寻优,最终得到最优的K个功率{Pk,total,k=1,2,…,K},分别代表分配给每个用户的功率值。然后利用每个用户的功率值Pk,total分别对每个用户进行单用户的功率分配,最终得到整个系统的最大容量。而在单用户功率分配当中,注水算法[22]可以实现最优的功率分配。但是,注水分配算法需要借助数学搜索的方式进行水位的计算,并且水位还会随时间进行周期性的更新,这无疑增加了算法的复杂度和系统负担。由于文献[15]已经通过仿真验证了等功率分配方式和注水算法所得到的系统容量几乎完全相同。所以,本文利用等功率的分配方式在每个用户下进行单用户的功率分配,那么第k个用户在其第n个子载波上分配的功率值pk,n可以表示为

pk,n=Pk,total/nk

(9)

式中,nk同式(2)的Nk,为分配给第k个用户的子载波数。

由以上分析和式(6)可知,本文利用SA-ABC算法要解决的问题就是在兼顾用户公平度的前提下,寻找一个由K个用户功率值所表示的最优蜜源,并在该蜜源下利用等功率的分配方式为每个用户进行单用户的功率分配,最终实现系统容量的最大化。此时系统的优化模型由式(6)变为

(b) Fairness≥ξ

(10)

为了兼顾系统容量和用户公平度,根据式(10),本文采用式(11)的外点惩罚函数作为SA-ABC算法的寻优适应度函数:

Fitness=

(11)

式中,Ωk表示分配给第k个用户的子载波集合;Fairness为用户公平度函数值;ξ为公平度约束;Fitnessmax为最差蜜源对应的适应度,当不存在可行解时,Fitnessmax=0。该适应度函数的优势体现在以下两点:

(1) 对于群体中满足公平度约束ξ的蜜源(即在可行域内),选择使目标函数最小的蜜源为最优解;

(2) 由于可行域中的蜜源都优于可行域外的蜜源,对于群体中不满足公平度约束ξ的蜜源(即在可行域外),使用Fitnessmax+(ξ-Fairness)对该蜜源进行惩罚,在这种惩罚力度下,群体中的所有蜜源都逐步向可行域内收敛。

根据式(11),本文基于惩罚函数的功率分配算法的详细步骤如下:

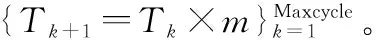
步骤2侦查蜂生成初始蜜源:首先侦查蜂在搜索域中搜索生成2SN个K维度的蜜源(即:每个蜜源都由K个功率值组成,并且K个功率值的和等于总发射功率的大小),搜索方式为随机搜索;然后利用式(11)计算这2SN个蜜源的花蜜量(即:适应度值Fitness),选择花蜜量较多的SN个蜜源作为初始标记蜜源,并找出这SN个花蜜量当中的最大值和最大值相对应的蜜源;最后将花蜜量的最大值作为初始最大花蜜量(即:最优适应度),将花蜜量最大值对应的蜜源作为初始最优蜜源(即:最优解)。

步骤3引领蜂搜索更优蜜源:为了寻找到更好的蜜源,在采蜜过程中引领蜂按照式(7)对SN个初始标记蜜源的邻域进行局部搜索。当引领蜂搜索完毕后,在温度控制参数Tk下,利用模拟退火思想对每个蜜源执行以下过程:

步骤3.1根据式(11)计算新蜜源的花蜜量Fitnessnew,如果Fitnessnew大于原蜜源的花蜜量Fitnessold,则用新蜜源取代原蜜源;否则,计算接受新蜜源的概率P=exp[(Fitnessnew-Fitnessold)/Tk]后,转到步骤2;

步骤3.2在区间(0,1)上产生一个随机数φ,如果P>φ,则用新蜜源取代原蜜源;否则,蜜源不发生变化,并令Bas=Bas+1。

经过以上过程,将最终得到的SN个较优蜜源作为标记蜜源,并更新这SN个标记蜜源的花蜜量值和Bas的值。

步骤4跟随蜂搜索蜜源:首先跟随蜂利用引领蜂传递的SN个标记蜜源和这SN个标记蜜源对应的花蜜量,根据式(8)以轮盘赌的方式选取更优的标记蜜源;然后跟随蜂按照式(7)在这些更优标记蜜源的邻域搜索新的蜜源后,在温度控制参数Tk下,按照步骤3中模拟退火的选择过程对每个蜜源进行相应选择;最后将最终得到的SN个蜜源作为本次采蜜过程的标记蜜源,并更新每个标记蜜源的Bas值。

步骤5判断是否出现侦察蜂:根据每个蜜源最大开采次数Limit和当前每个蜜源的开采次数Bas判断是否将引领蜂转变为侦查蜂。对某个蜜源,若Bas>Limit,表示这个蜜源在Limit次开采后没有改进,则原来的这个蜜源被放弃,同时相应的引领蜂转变为侦查蜂后随机搜索一个新的蜜源代替被放弃的蜜源。

步骤6对最优解进行更新:首先按照式(11)更新本次采蜜过程中SN个标记蜜源的花蜜量;然后找出这SN个花蜜量的最大值;最后判断是否更新最优蜜源和最大花蜜量。

步骤7判断当前进化代数cycle是否满足终止条件Maxcycle:若cycle=Maxcycle,则输出最大花蜜量(即最优适应度);否则,计算新的温度控制参数Tk+1=Tk×m并转到步骤3。

4 仿真分析

本文的仿真中,信道模型为具有频率选择性的多径瑞利信道,信道多径数为6,信道功率时延服从指数衰减,均方时延扩展为5 μs,总信道带宽为B=1 MHz,总发送功率为Ptotal=1 W,AWGN的功率谱密度为-80 dB·W/Hz,子载波数N=64。本文的SA-ABC算法中SN=100,Limit=30,Maxcycle=100,m=0.9,T0=100,并且为了更好地比较算法的性能,在仿真中设置:R1∶R2∶…∶RK=1∶1∶…∶1,仿真结果为500次仿真取平均。本文仿真中用于对比的是文献[12]的Shen算法和文献[16]的AFSA算法。

由图2可知,当ξ=1时,随着用户数目的增多,本文提出的子载波分配算法(Proposed-SAA)所实现的系统容量要比文献[12]的Shen算法中的子载波分配部分(Shen-SAA)所实现的系统容量高,但比AFSA算法子载波分配部分(AFSA-SAA)实现的系统容量低。但由图3可知,当ξ=1时,本文的Proposed-SAA算法所实现的用户公平度几乎和Shen-SAA一样,要远远好于AFSA-SAA所实现的用户公平度。特别当放松公平度约束为ξ=0.99时,图2显示本文的Proposed-SAA算法所实现的系统容量将有一定的提升。

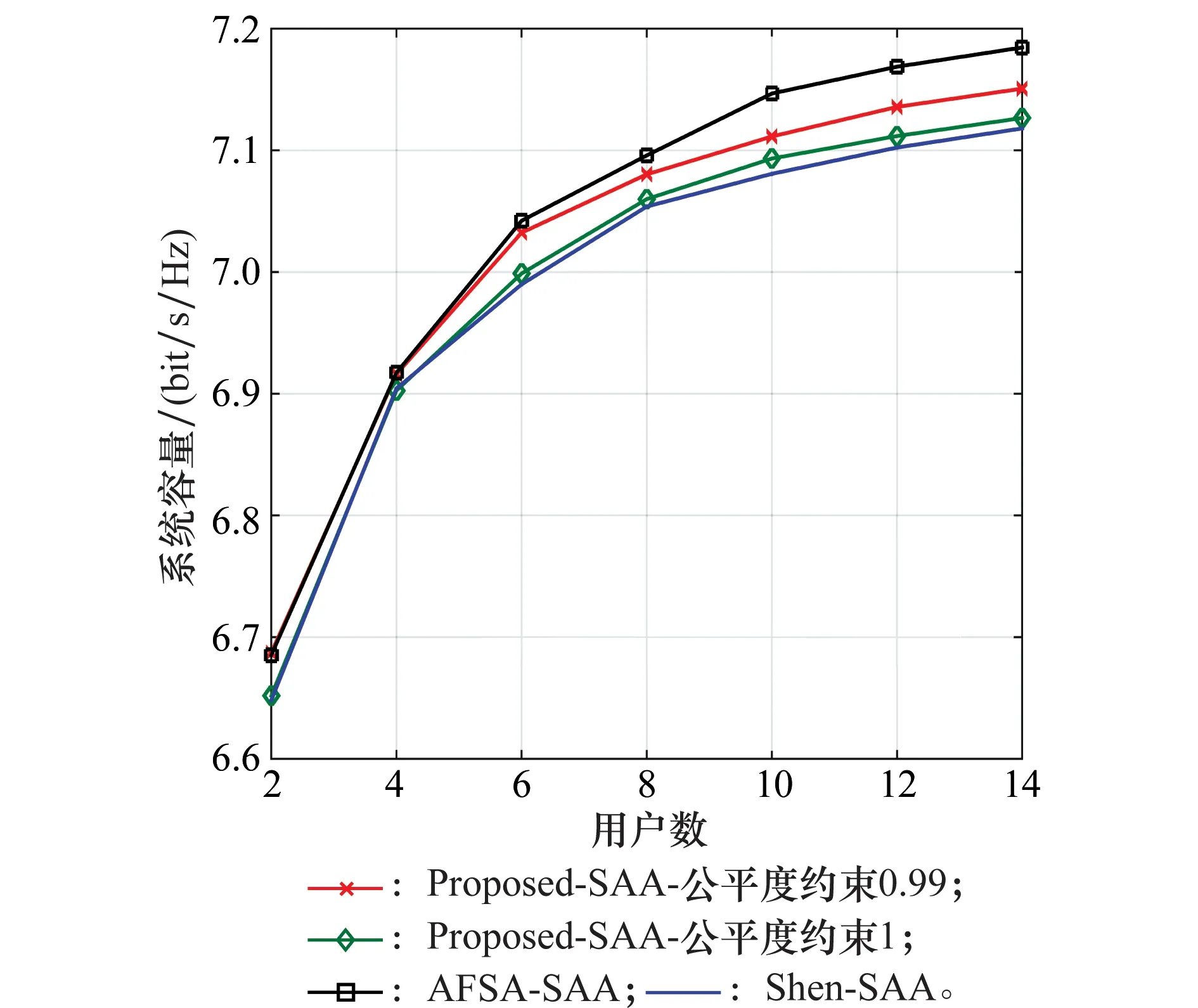
图2 不同子载波分配算法的系统容量Fig.2 System capacity of different subcarrier allocation algorithms

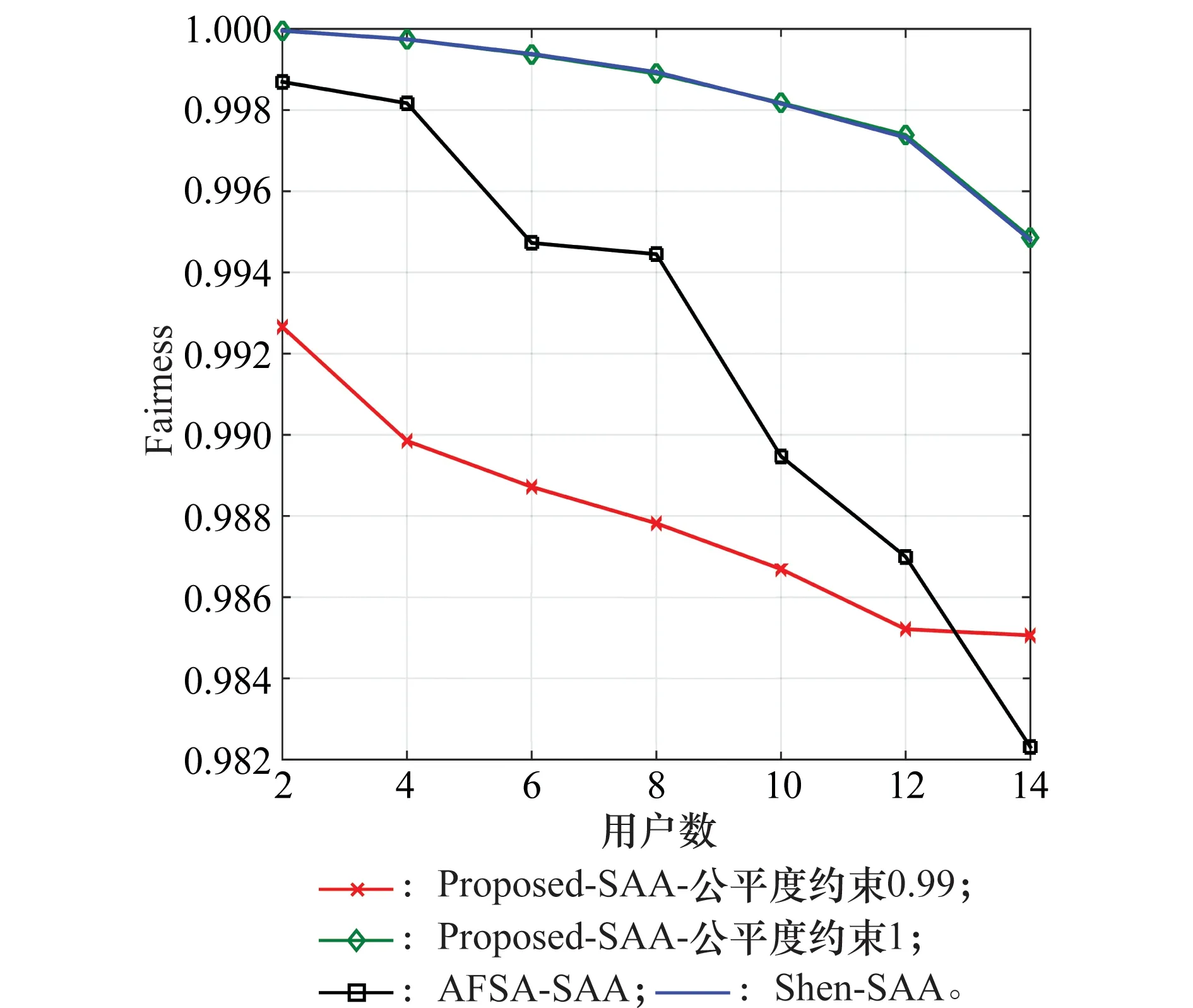
图3 不同子载波分配算法的用户公平度Fig.3 User fairness of different subcarrier allocation algorithms

由图3可知,当ξ=0.99时,本文的Proposed-SAA算法所实现的用户公平度有所降低,并且在用户数较少时,ASFA-SAA的公平度较好,但当用户数目增多时(K=14时),本文的Proposed-SAA算法所实现的用户公平度要好于ASFA-SAA所实现的的用户公平度。这是因为当用户数增加时,可以被AFSA-SAA调用的子载波就减少了,相应的各用户之间使用子载波的自由度就降低了,进而导致每分配一个子载波都会影响其他用户的公平度。所以,在子载波数目不变的前提下,随着用户数目的增多,AFSA-SAA所实现的用户公平度将越来越差。

由图3还可以知道,虽然给定公平度约束为ξ=0.99,但本文的Proposed-SAA算法所实现的用户公平度并不能满足公平度约束ξ的要求。这是因为当用户的公平度低于0.99时,本文的Proposed-SAA算法将自动地提升用户的公平度,但是随着子载波分配的进行,可以使用的子载波数渐渐变少,当本文的Proposed-SAA算法对用户公平度的提升不足以弥补ξ与实际用户公平度之差时,就会出现用户的公平度略低于公平度约束ξ的现象。

结合图2和图3可以得出,本文的Proposed-SAA算法可以单独实现较好的用户公平度或者较高的系统容量,但不能较好地兼顾系统容量和用户公平度。

图4和图5是当ξ=0.99时,本文子载波分配算法和本文子载波分配算法与功率分配算法的联合算法(Proposed-SAA-SA-ABC)的仿真对比图。

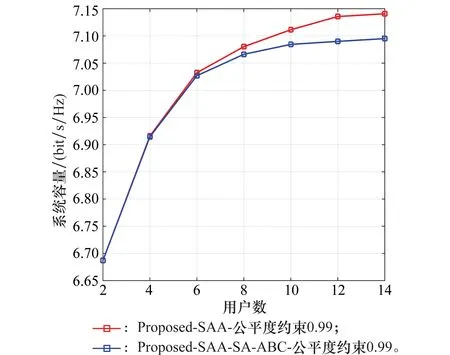
图4 系统容量比较Fig.4 Comparison of system capacity

由图4可知,在SA-ABC算法的功率分配完成后,系统的容量要比子载波分配后降低了。而图5显示在SA-ABC算法的功率分配完成后,用户的公平度满足了公平度约束ξ的要求。结合图2～图5可得出,虽然本文的子载波分配算法不能较好地兼顾系统容量和用户公平度,但经过本文算法的功率寻优后,用户的公平度基本满足了公平度约束ξ的要求,而这种公平度的提升是以牺牲系统容量为代价的。

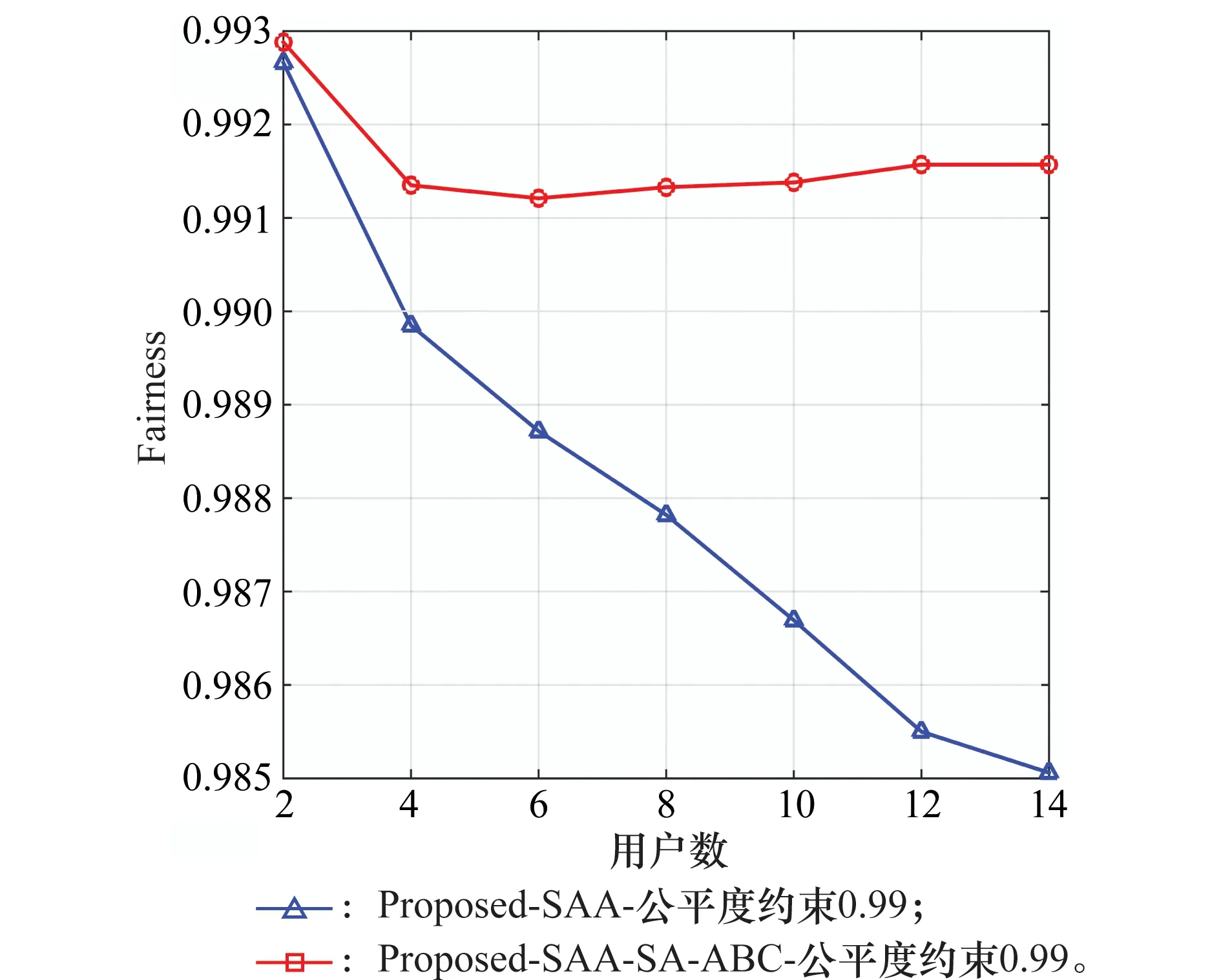
图5 用户公平度比较Fig.5 Comparison of user fairness

图6是当ξ=0.5,0.9,0.95,0.99时,随着用户数目的增加,本文提出的联合算法(Proposed-SAA-SA-ABC)、本文的子载波分配与普通ABC算法所组成的联合算法(SAA-ABC)、Shen算法、AFSA算法以及OFDM-TDMA算法所实现的系统容量对比情况。

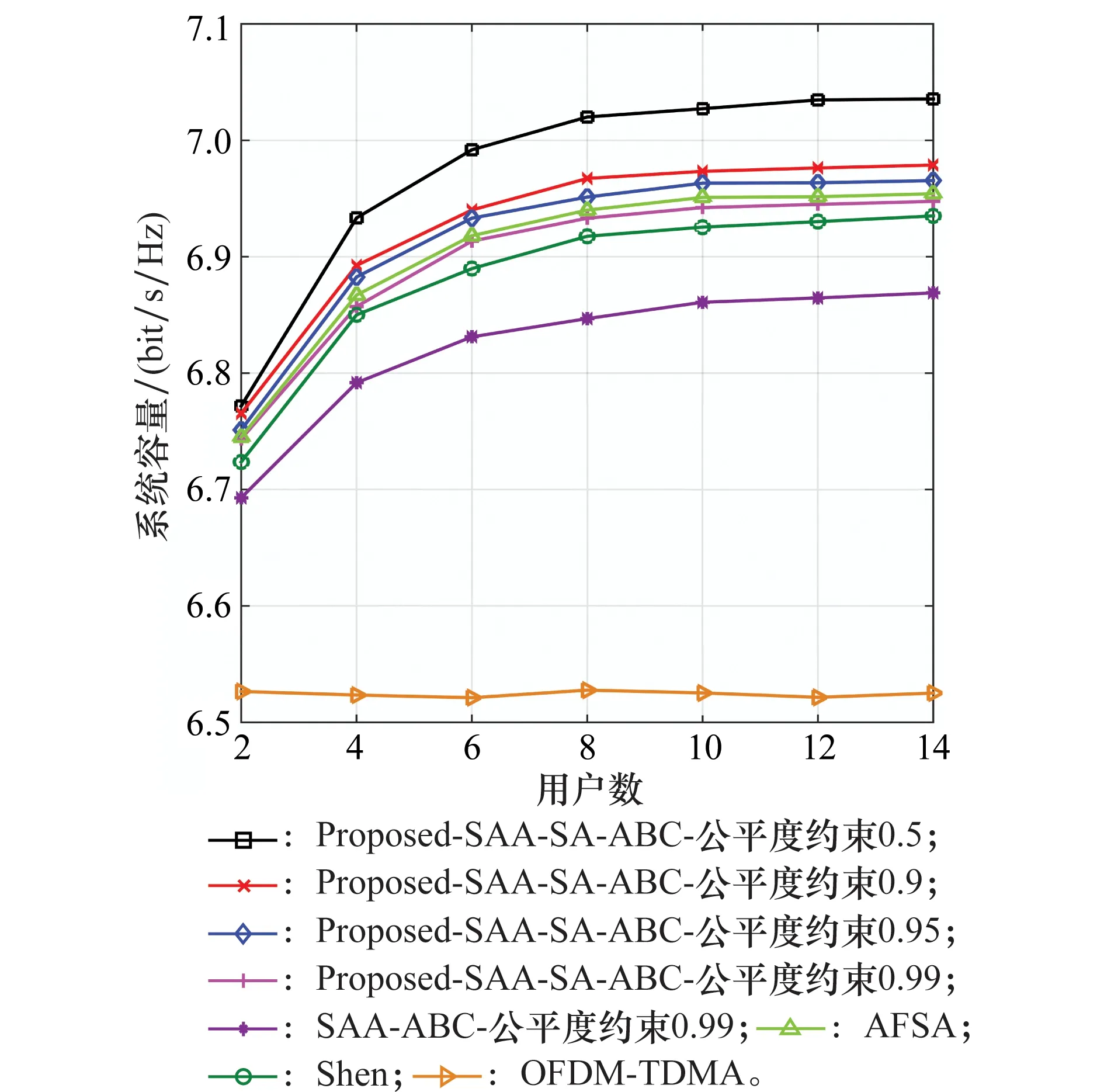
图6 不同算法的系统容量Fig.6 System capacity of different algorithms

由图6可知,本文Proposed-SAA-SA-ABC算法的系统容量要好于SAA-ABC算法所实现的系统容量。这是因为SA-ABC算法摈弃了ABC算法的贪婪选择策略,使用可以跳出局部极值的模拟退火策略,进而得到了更好的适应度值。由图6还可以知道,本文的Proposed-SAA-SA-ABC算法的系统容量要好于Shen算法的系统容量。而当ξ=0.99时,AFSA算法的系统容量略好于本文Proposed-SAA-SA-ABC算法的系统容量。但当降低公平度约束ξ为0.95、0.9和0.5时,本文Proposed-SAA-SA-ABC算法的系统容量将有大幅度的提升,并优于AFSA算法所实现的系统容量,从而说明本文提出的联合算法可以在用户公平度和系统容量之间进行灵活的调整。

图7中给出了当用户数K=8,ξ=0.99时,本文Proposed-SAA-SA-ABC算法与AFSA算法的适应度收敛曲线。

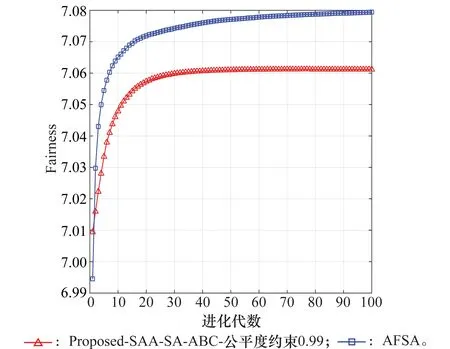
图7 适应度收敛曲线Fig.7 Convergence curve of fitness

由图7可知,虽然在ξ=0.99时,本文算法的最优适应度没有AFSA算法的最优适应度好,但随着迭代次数的增加,本文算法率先收敛到最优适应度,进而说明本文的Proposed-SAA-SA-ABC算法具有更好的收敛能力。

为了不失一般性,当用户数K=8、ξ=1、平均子信道信噪比为20 dB、式(1)的约束条件(c)为R1∶R2∶…∶R8=6∶4∶2∶1∶1∶1∶1∶1时,图8给出了每个用户的归一化速率比例分配情况。

图8 各用户的归一化速率比例Fig.8 Normalized rate proportionality for each user

由图8中可知,本文Proposed-SAA-SA-ABC算法实现的用户公平度几乎和理想的用户公平度一致。而AFSA算法所实现的用户公平度相对较差,传统的静态资源分配方案OFDM-TDMA几乎不能兼顾用户的公平度。从而说明了本文的Proposed-SAA-SA-ABC算法不仅保证了OFDMA系统中各个用户的高容量,同时也保证了各用户容量之间的公平。

5 结束语

本文针对基于RA准则的OFDMA自适应资源分配中,系统容量和用户公平度的问题,提出了一种基于公平度进行子载波分配和基于惩罚函数进行功率分配的OFDMA自适应资源分配方案。在该方案中,通过改进基于RA准则的OFDMA自适应系统优化模型,只要给出公平度约束值ξ,就可以得到相应的最优解。仿真结果显示,本文所提方案可以根据用户的需求灵活地调整系统容量和用户公平度,在保证满足公平度约束ξ的同时,有效地实现了系统容量的最大化。所以,本文所提出的方案是在最大化系统容量和用户公平度之间的折中。同时,该方案也为后续对基于RA准则的OFDMA自适应资源分配的研究,提供了一条有效的途径。

[1] 朱晓荣,罗小琴,朱洪波.正交频分多址系统中一种面向多业务应用的自适应资源分配算法[J].电子与信息学报,2015, 37(6): 1298-1303.

ZHU X R, LUO X Q, ZHU H B. Adaptive resource allocation scheduling algorithm for multi-service application in OFDMA system[J].Journal of Electronics and Information,2015,37(6):1298-1303.

[2] 左勇, 刘学勇, 刘海洋, 等. 基于对偶分解的 OFDMA系统资源分配算法[J]. 电子与信息学报, 2012, 34(12): 2843-2849.

ZUO Y, LIU X Y, LIU H Y, et al. A dual-decomposition-based resource allocation algorithm for OFDMA systems[J]. Journal of Electronics and Information, 2012, 34(12):2843-2849.

[3] WU Q Q, CHEN W, TAO M X, et al. Resource allocation for joint transmitter and receiver energy efficiency maximization in downlink OFDMA systems[J]. IEEE Trans.on Communications, 2015, 63(2):416-430.

[4] YIN S X, QU Z W. Resource allocation in multiuser OFDM systems with wireless information and power transfer[J]. IEEE Communications Letters, 2016, 20(3): 594-597.

[5] 朱继华,王竟鑫,申茜,等. OFDM系统中一种改进的低复杂度自适应比特功率分配算法[J]. 重庆邮电大学学报(自然科学版),2017, 29(2): 202-207.

ZHU J H, WANG J X, SHEN Q, et al. An improved adaptive bit power allocation algorithm with the low complexity for OFDM system[J]. Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition),2017,29(2):202-207.

[6] KIBRIA M G, SHAN L. Resource allocation optimization for users with different levels of service in multicarrier systems[J]. IEEE Signal Processing Letters, 2015,22(11):1869-1873.

[7] VAR P, SHRESTHA R, KIM J M. Improved power allocation to enhance the capacity in OFDMA system for proportional resource allocation[J]. The Journal of Korean Institute of Communications and Information Sciences, 2013,38(7):580-591.

[8] YIN Z D, ZHUANG S F, WU Z L, et al. Rate adaptive based resource allocation with proportional fairness constraints in OFDMA systems[J]. Sensors, 2015, 15(10): 24996-25014.

[9] ABD-ELNABY M, SEDHOM G G, MESSIHA N W, et al. Fair subcarrier-power allocation scheme for multiuser multicarrier systems[J].Journal of Central South University,2015,22(8):3033-3041.

[10] AHMED I, SADEQUE S, PERVIN S. Margin adaptive resource allocation for multi-user OFDM systems by particle swarm optimization and differential evolution[J]. International Journal of Engineering and Technology, 2011:227-231.

[11] WONG I C, EVANS B L. Optimal downlink OFDMA resource allocation with linear complexity to maximize ergodic rates[J]. IEEE Trans.on Wireless Communications,2008,7(3):962-971.

[12] SHEN Z K, ANDREWS J G, EVNANS B L. Adaptive resource allocation in multiuser OFDM systems with proportional rate constraints[J]. IEEE Trans.on Wireless Communications, 2005,4(6):2726-2737.

[13] ZHAO W T, WANG S W. Joint subchannel and power allocation in multiuser OFDM systems with minimal rate constraints[J]. International Journal of Communication Systems,2014,27(1):1-12.

[14] REN Z Y, CHEN S Z, HU B, et al. Proportional resource allocation with subcarrier grouping in OFDM wireless systems[J]. IEEE Communications Letters, 2013,17(5):868-871.

[15] JANG J H, LEE K B. Transmit power adaptation for multiuser OFDM systems[J]. IEEE Journal on Selected Areas in Communications, 2003, 21(2): 171-178.

[16] 汪照, 李有明, 陈斌, 等. 基于鱼群算法的 OFDMA自适应资源分配[J]. 物理学报, 2013,62(12):509-515.

WANG Z, LI Y M, CHEN B, et al. OFDMA adaptive resource allocation based on fish swarm algorithm[J]. Acta Physica Sinica, 2013, 62(12): 509-515.

[17] LIU M Z, LI X, ZHANG M Y, et al. Research on artificial fish swarm algorithm with cultural evolution for subcarrier allocation[J]. International Journal of Hybrid Information Technology, 2015, 8(6):279-288.

[18] XU L, LI Y P, LI Q M, et al. Proportional fair resource allocation based on hybrid ant colony optimization for slow adaptive OFDMA system[J]. Information Sciences, 2015, 293:1-10.

[19] SHARMA N, MADHUKUMAR A S. Genetic algorithm aided proportional fair resource allocation in multicast OFDM systems[J]. IEEE Trans.on Broadcasting, 2015, 61(1): 16-29.

[20] 兰海燕,杨莘元,刘海波,等.基于文化算法的多用户OFDM系统资源分配[J].吉林大学学报:工学版,2011,41(1):226-230.

LAN H Y, YANG S Y, LIU H B, et al. Resource allocation for multiuser OFDM system based on cultural algorithm[J]. Journal of Jilin University: Engineering Science Edition, 2011, 41(1): 226-230.

[21] ARCHANA C, REJITH K N. Rate adaptive resource allocation in OFDMA using BEES algorithm[J]. International Journal of Research in Engineering and Technology, 2014, 3(15): 14-18.

[22] XU L, ZHOU X Z, LI Q M, et al. Energy-efficient resource allocation for multiuser OFDMA system based on hybrid genetic simulated annealing[J]. Soft Computing, 2016:1-8.

[23] CHEN S Z, REN Z Y, Hu B, et al. Resource allocation in downlink ofdm wireless systems with user rate allowed regions[J]. Wireless Personal Communications, 2015, 80(1): 429-445.