矩阵对角化变换鲁棒QCKF在视觉和惯性融合姿态测量中的应用

郭肖亭, 孙长库,2, 王 鹏,2

(1. 天津大学精密测试技术及仪器国家重点实验室, 天津 300072; 2. 中航工业洛阳电光设备研究所光电控制技术重点实验室, 河南 洛阳 471009)

0 引 言

姿态确定问题是头盔姿态确定问题[1]、头盔瞄准定位[2]、无人机飞行控制[3]、增强现实[4]等领域的关键性问题之一,在工程实践和科学研究中有重要的理论和实践意义。单一姿态测量方法在精度、速度等方面因自身技术的限制,难以满足测量需求,多传感器融合姿态测量技术[5]应用而生。将视觉和惯性融合进行姿态测量,可以发挥视觉方法重复性和稳定性好[6-7]以及惯性方法更新频率高、不受环境光干扰的特点[8],实现各传感器的优势互补。

针对视觉、惯性融合视觉和惯性融合测量的相关问题,国内外学者进行了大量的研究和探索[9-13]。在实际应用中,融合姿态测量的系统模型通常是非线性或/和非高斯,因此通常使用扩展卡尔曼滤波(extended Kalman filter, EKF)[14]、无迹卡尔曼滤波(unscented Kalman filter, UKF)[15]、容积卡尔曼滤波(cubature Kalman filter, CKF)[16-18]等适合于计算机迭代处理的非线性滤波算法进行多传感器融合。EKF是高斯白噪声假设下典型的非线性滤波方法,但EKF存在理论上的局限性,其一阶线性截断误差使得滤波精度低甚至导致滤波发散,尤其在系统非线性较强、存在未知干扰或状态突变等情况下。UKF不对系统模型进行线性化处理, 将对非线性系统的函数近似转换成对其后验概率密度的近似,实现简单,滤波效果优于EKF。CKF采用一组等权值的容积点集来计算后验概率密度,相比EKF和UKF,具有更优的非线性逼近性能、数值精度。

上述非线性滤波算法都属于高斯滤波器,即假设状态的后验分布和预测分布近似为高斯分布。而在实际应用中,往往存在着模型不确定性或/和噪声统计特性不完全已知,这些不确定因素会造成传统的非线性卡尔曼滤波算法失去最优性,使得估计精度降低甚至滤波发散。而基于鲁棒控制理论的H∞滤波算法[19]与卡尔曼滤波器采用最小方差估计准则不同,该算法使用极大极小准则,不需要知道环境噪声的统计特性等先验信息,通过使噪声能量和估计误差能量的最大比值小于某一个正数,确保外界干扰对状态估计结果的影响最小,因此该算法对系统模型误差和外界干扰具有更强的鲁棒性。将H∞鲁棒滤波算法和CKF相结合,形成鲁棒CKF滤波策略,可以克服系统非线性、非高斯特性以及突变型不良测量对滤波带来的影响,提高测量系统的滤波精度以及鲁棒性。针对计算误差、舍入误差、模型失准等原因造成协方差矩阵失去正定性而往往出现滤波中断的问题,使用矩阵对角化变换代替标准CKF算法中的Cholesky分解[20],提高滤波稳定性。姿态参数采用计算量小、可全姿态工作且不存在奇异性的四元数,针对其在非线性滤波中易出现协方差矩阵奇异性的问题,使用乘性误差四元数三维矢量进行预测值和方差的计算,以保持滤波算法的稳定性。

搭建了惯性和视觉多传感器融合姿态测量系统,针对系统中各传感器坐标系以及辅助坐标系不一致的问题,通过将各传感器测量值转换到目标坐标系中完成测量系统坐标系的统一,将提出的基于矩阵对角化变换的鲁棒四元数容积卡尔曼滤波(quaternion cubature Kalman filter,QCKF)算法在实验平台上进行验证,并与标准CKF进行对比,验证本文算法的有效性。

1 视觉和惯性融合姿态测量原理

融合姿态测量原理如图1所示。惯性测量单元(inertial measurement unit,IMU)和目标物体固定连接,摄像机正对与目标物体固定连接的立体靶标。在目标物体运动过程中,IMU以初始姿态为基准,测量其相对空间惯性坐标系姿态;摄像机拍摄立体靶标运动图像,通过对特征点图像坐标分析计算,完成视觉姿态测量。

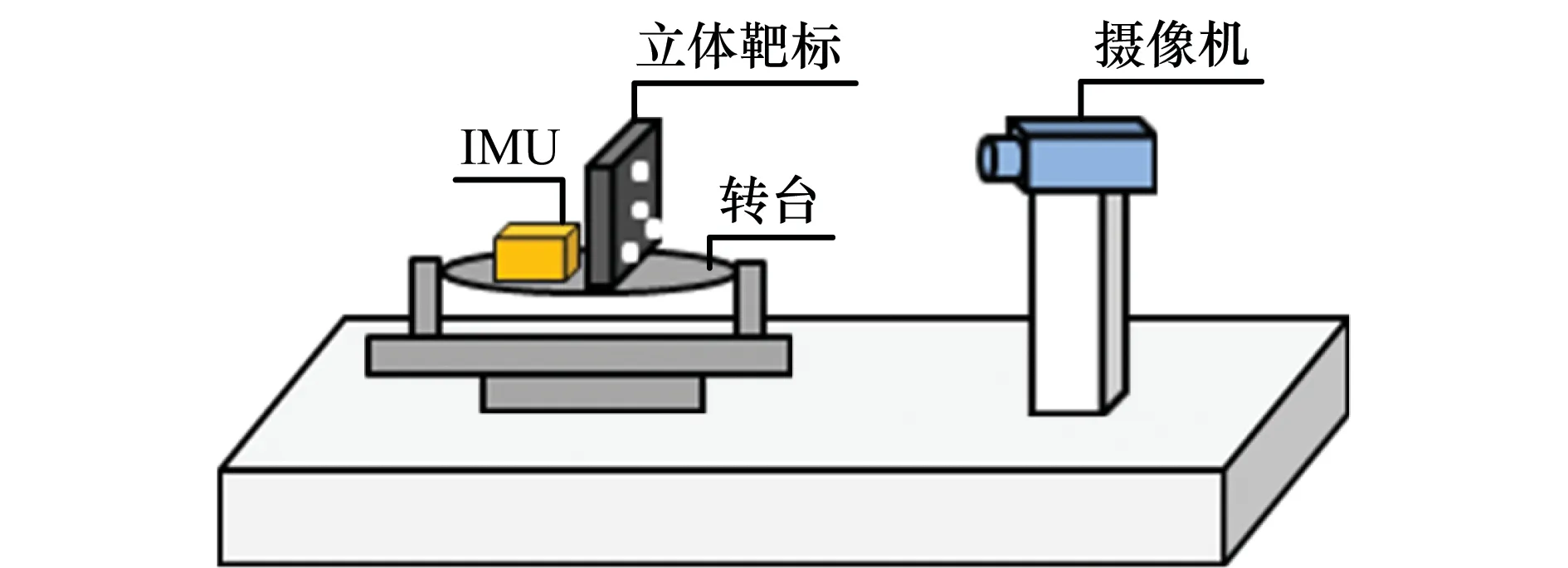
图1 姿态测量系统结构示意图Fig.1 Schematic diagram of fusion measurement system

惯性测量和视觉测量在不同的坐标系中进行并且各自的测量姿态与目标物体运动姿态存在差异,因此对测量系统坐标系进行统一。定义ObXbYbZb、OcXcYcZc、OtXtYtZt、OnXnYnZn分别表示运动物体坐标系(b系)、摄像机坐标系(c系)、靶标坐标系(t系)以及IMU坐标系(n系),如图2所示。测量中使用低精度的微机电系统(micro-electro-mechanical system,MEMS)-IMU,其无法感测地球自转角速率,因此可选取和地球固定连接的坐标系为近似空间惯性坐标系OiXiYiZi,本文中选取c系。坐标系统一的目标可表述为将惯性测量和视觉测量均转换到目标物体在c系中的旋转姿态。

(1)

(2)

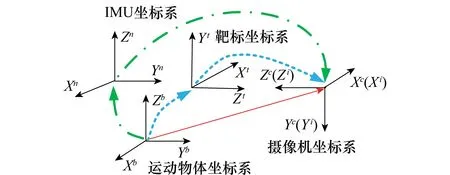
图2 测量系统坐标系统一Fig.2 Coordinate system normalization

2 视觉和惯性融合姿态测量算法

2.1 视觉姿态测量

视觉姿态测量方法是使用摄像机拍摄运动物体上特征点,根据特征点在摄像机中成像坐标的变化,结合已知特征点在被测物体上的布局坐标,实现对被测物体姿态的测量[6-7]。本文视觉测量结构采用由外向内的方法,即特征点布置在运动体上,而摄像机固定在环境中并朝向被测物,在室内近距离高精度定姿尤其是头部跟踪应用场景中,此种测量结构与由内向外的视觉测量结构相比更实用。立体靶标由4个非共面红外LEDs组成,为视觉测量的特征点,各个特征点之间的相对空间几何关系已知。使用红外特征点是为了避免环境中杂散光源在图像处理过程中进行特征识别时带来干扰。使用4个非共面特征点可以保证在较大的运动范围内仍可以正确识别各个特征点。

在较大的运动范围内使用较少的特征点进行视觉姿态测量,比例正交投影迭代变换(pose from orthography and scaling with iterations,POSIT)是比较经典的非线性迭代算法;而POSIT算法的测量精度与测量范围有关,小范围内可以达到较高的测量精度,随测量范围增加精度会相应地降低。针对此问题本文使用基于约束校准的姿态测量算法[6]。标准POSIT算法以初始位置为基准进行相对姿态测量,如图3中A方案所示;而约束校准算法采用图3中B方案,先标定后测量。首先对全空间进行标定,建立基准位置,空间基矢量,基准姿态的一一对应关系;测量阶段寻找距离待测量位置最近的基准点,则待测位置姿态可表示为基准姿态与待测位置相对基准位置姿态的代数和为

θx=θbase+θbase-x

(3)

式中,θx,θbase,θbase-x分别表示待测量位置姿态、选定基准位置姿态以及待测位置相对基准位置姿态。

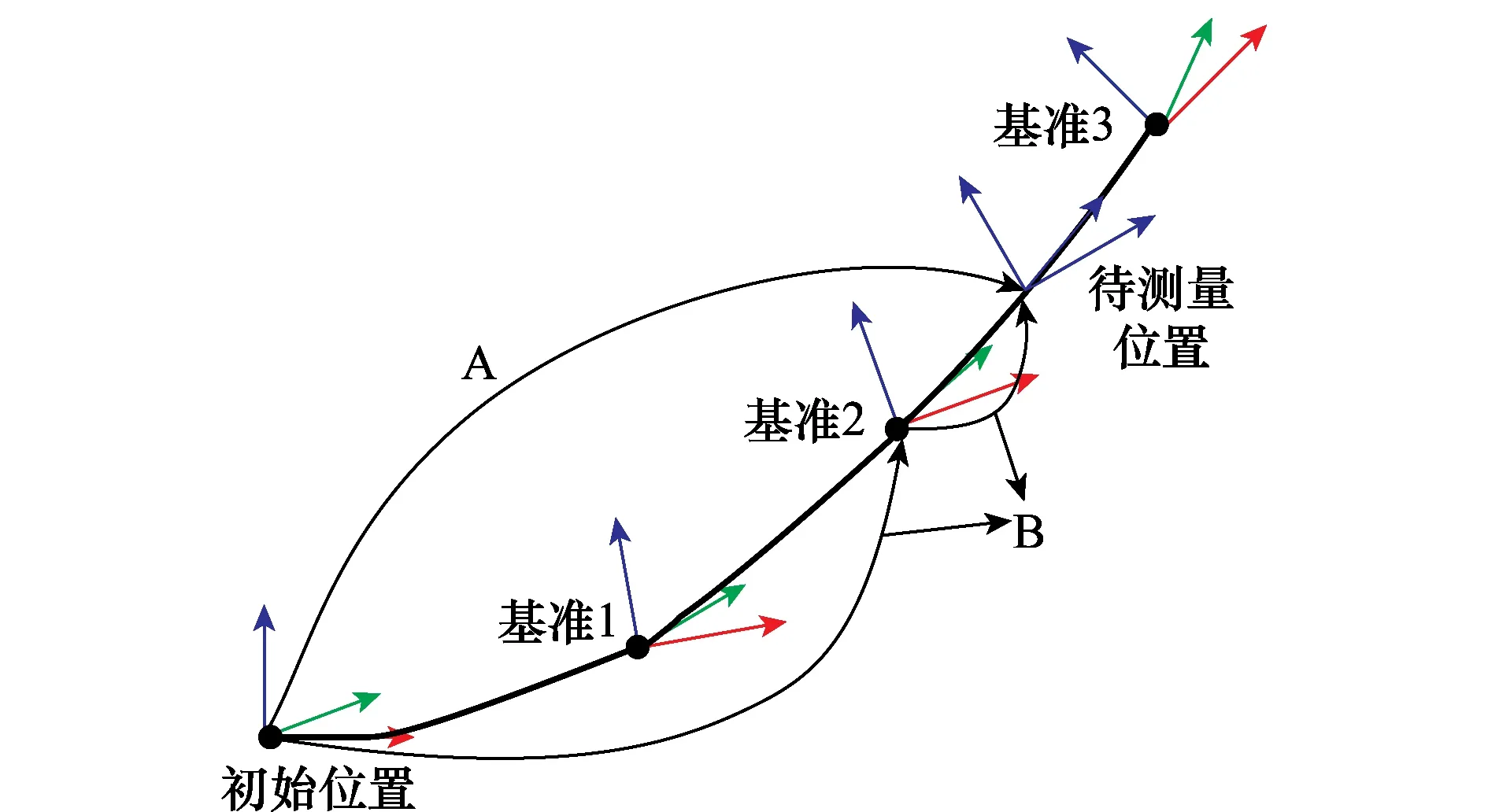
图3 POSIT算法和约束校准算法对比Fig.3 Contrast of POSIT and restrain calibration algorithm

2.2 陀螺仪模型

惯性姿态测量借助IMU中三自由度陀螺仪完成。陀螺仪感测目标物体运动,输出角速度,通过姿态解算算法实现惯性姿态测量。陀螺仪输出中存在许多误差项,需要对其进行标定补偿。陀螺仪输出可建模为

(4)

零位偏差的标定可采用每次测量之前先标定的方法[21]。传感器上电后先保持陀螺仪水平静止测量几组数据,对每组数据计算漂移角度,然后时间和漂移角度进行高阶多项式曲线拟合获取拟合系数,将每组数据拟合系数取均值得到标定拟合系数并保存。测量过程中根据标定拟合系数和采样时间估计漂移角度,从漂移角度反算得到偏差值,陀螺仪输出减去反算偏差对原始输出中的零位偏差进行补偿。具体过程如图4所示。而对于与时间有关的随机漂移的补偿,可将其包含在滤波状态量中,在每次滤波循环中对其不断更新,从而进一步对陀螺仪输出量进行补偿。

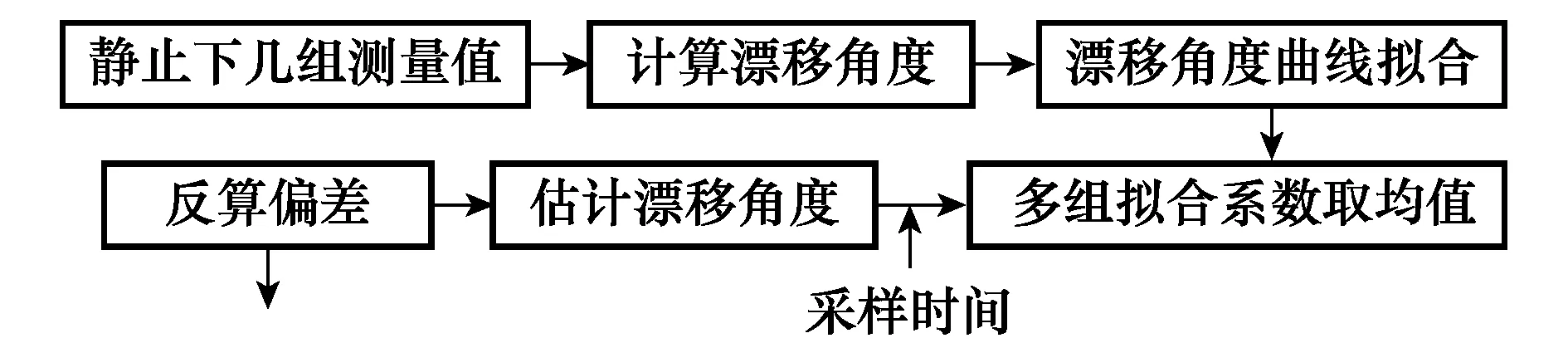
图4 陀螺仪零位偏差标定及补偿Fig.4 Calibration and compensation of gyroscope bias

2.3 矩阵对角化变换

标准CKF算法中使用Cholesky分解进行协方差矩阵的分解,而Cholesky分解要求待分解矩阵具有正定性。当协方差矩阵失去正定性时可导致滤波立即中断,对算法稳定性提出了极大的挑战。滤波中断多发生在滤波进行过多次之后由于模型失配、计算误差等造成的协方差矩阵非正定。而基于矩阵对角化变换的方法对协方差矩阵进行分解,不需要矩阵具有正定性。

定理1设A为n阶实对称矩阵,则必有n阶正交矩阵V,使得VTAV=V-1AV=D,即A=VTDV,其中D是以A的n个特征值为对角元素的对角阵。

而在卡尔曼滤波过程中协方差矩阵P是实对称矩阵,由定理1立即可得P=VTDV,其中D是以P的n个特征值为对角元素的对角阵,V为n个特征值对应的两两正交的特征向量构成的正交矩阵阵,令

(5)

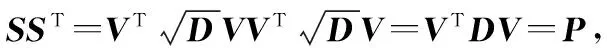
2.4 基于矩阵对角化变换的鲁棒四元数容积卡尔曼滤波

不同于卡尔曼滤波基于使估计误差的方差最小化的思想,H∞滤波是基于极大极小鲁棒控制准则的滤波算法,即最小化可能存在最大误差,具体指的是在对滤波初始状态、系统噪声、观测噪声等先验信息未知的条件下获取状态量的最佳估计值,定义代价函数

(6)

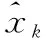
引入约束条件γ,有

(7)

式(7)可改写为

(8)

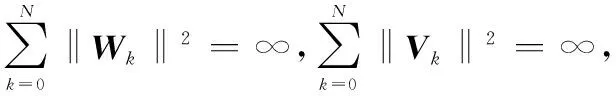
(9)

将H∞滤波应用到CKF中对H∞滤波方法中状态估计协方差矩阵的递推方程进行转换

Pk+1=Pk+1|k-

(10)

如果对任意时刻γ取满足条件pk>0的最小值,则可以得到最优H∞滤波。当γ→∞时,H∞滤波器退化为卡尔曼滤波器。当取最小值时滤波器的鲁棒性最好,但估计方差不一定最小;当γ→∞时则可以得到最小方差估计,但鲁棒性较差。因此通过适当选择的值,调节系统在测量精度和系统鲁棒性之间的平衡,以满足测量需要。

CKF采用一组等权值的容积点集来计算后验概率密度[14],对于模型精确系统的状态估计精度可达到3阶,但是当存在较大系统模型误差或系统状态存在突变的情况,仍会产生较大的估计误差。在实际应用中,单一的CKF算法有时难以满足测量需求,将QCKF和H∞鲁棒滤波相结合,在CKF算法的框架中,将H∞滤波的鲁棒特性加入到协方差矩阵更新计算中,并使用矩阵对角化变换代替标准CKF中的Cholesky分解,增加滤波算法的计算稳定性。具体过程如下。

步骤1计算容积点

(11)

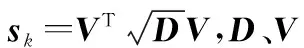
(12)

四元数和陀螺仪漂移部分容积点相应为

(13)

式中,i=1,2,…,n。

步骤2计算经过状态方程传递后的容积点

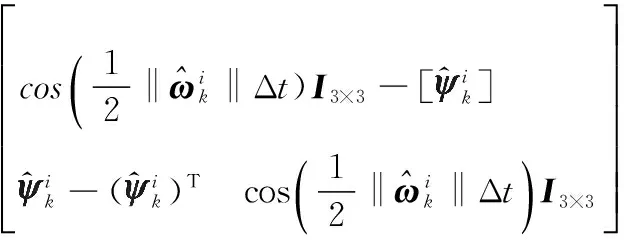
(14)

(15)

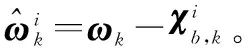
步骤3计算k+1时刻的状态预测值

(16)

式中

(17)

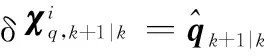
(18)

(19)

步骤4计算k+1时刻状态误差协方差矩阵

(20)

式中

步骤5计算更新后的状态容积点

(21)

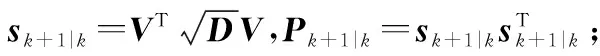
(22)

步骤6计算经过测量方程的容积点

(23)

(24)

式中,i=1,2,…,n。

步骤7计算k+1时刻的测量预测值

(25)

(26)

(27)

步骤8估计k+1时刻的测量误差协方差和一步预测互协方差矩阵

(28)

(29)

步骤9计算k+1时刻的滤波增益矩阵

(30)

步骤10计算k+1时刻的状态估计值

(31)

(32)

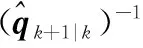
(33)

(34)

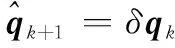
(35)

步骤11使用式(10)进行k+1时刻的状态误差协方差矩阵更新。

该方法将CKF和H∞滤波结合,发挥CKF算法的高精度和H∞滤波的鲁棒性的特点,使用矩阵对角化变换改善数值计算的稳定性。视觉和惯性融合测量系统,在保持与惯性高频率输出的同时,在视觉和惯性数据重合时刻进行滤波,用视觉数据抑制融合姿态随时间漂移,获取高频率、稳定、高精度的融合测量输出。

3 实验验证及结果分析

视觉和惯性融合姿态测量系统装置如图5所示。实验中转台为目标运动物体,IMU、立体靶标通过螺丝安装在转台上,摄像机朝向靶标放置,计算机控制转台运动、操作传感器进行测量并对测量数据进行分析计算。其中实验中使用的三维立体靶标结构如图6所示,各特征点之间的空间几何关系在图中标示,外围3个LEDs在同一平面内为等边三角形3个顶点,中心LED位于三角形中心且距离平面25 mm。

图5 测量系统实验平台Fig.5 Measurement system experimental platform

图6 立体靶标Fig.6 Three-dimensional target

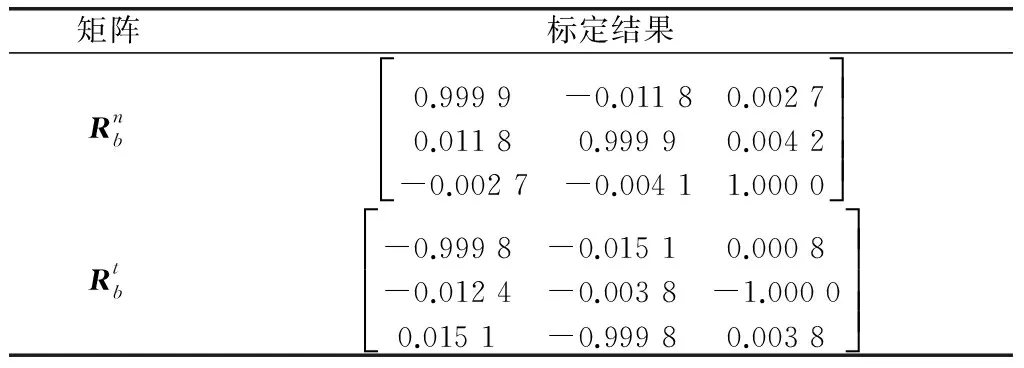
表1 测量系统中固定旋转矩阵标定结果

在测量过程中,转台根据设计路径进行运动,固定在转台上的IMU和立体靶标随转台一起转动,运动的同时进行IMU测量数据采集以及摄像机拍摄立体靶标在不同姿态下的图像如图7所示;对拍摄图像进行处理提取特征点,结合各个特征点的几何空间坐标关系,使用约束校准方法求解视觉姿态测量值。视觉姿态测量值和IMU测量数据结合,使用不同的融合算法,完成融合姿态量的求解。其中惯性数据采集周期为0.01 s,视觉数据采集周期为1.8 s。

图7 不同姿态拍摄图像特征点提取Fig.7 Processed images of target from different attitudes

为了对基于矩阵对角化变换的鲁棒CKF方法的有效性进行验证,在不同的运动形式下将其与标准CKF、纯惯性姿态测量以及视觉姿态测量进行对比。主要进行了转台绕不同的旋转轴的单轴运动,如图8～图10所示,以及转台俯仰轴和方位轴交替运动的两轴运动,两轴交替运动的具体运动方式为

(1)Z=-36°,X=-24°～ +24°;

(2)Z=-33°,X=+24°～-24°;

⋮

(25)Z=+36°,X=-24°～ +24°。

其中,X指代俯仰轴,Z指代方位轴。方位角阶梯式上升从负的最大值运动到正的最大值,在方位角每增加3°的运动过程中,俯仰角往返运动具体如图11所示。

对转台单、双轴运动形式下不同算法的姿态角、姿态角误差输出图形(见图8～图12)以及对应的均方根误差(root-mean-square error,RMSE)数据表2、表3进行分析可知,将惯性和视觉进行融合求解姿态,可抑制纯惯性测量角度漂移现象,保持视觉测量的稳定性,使融合姿态更新速率与惯性保持一致;同时改进的鲁棒CKF与标准CKF相比准确度较好。

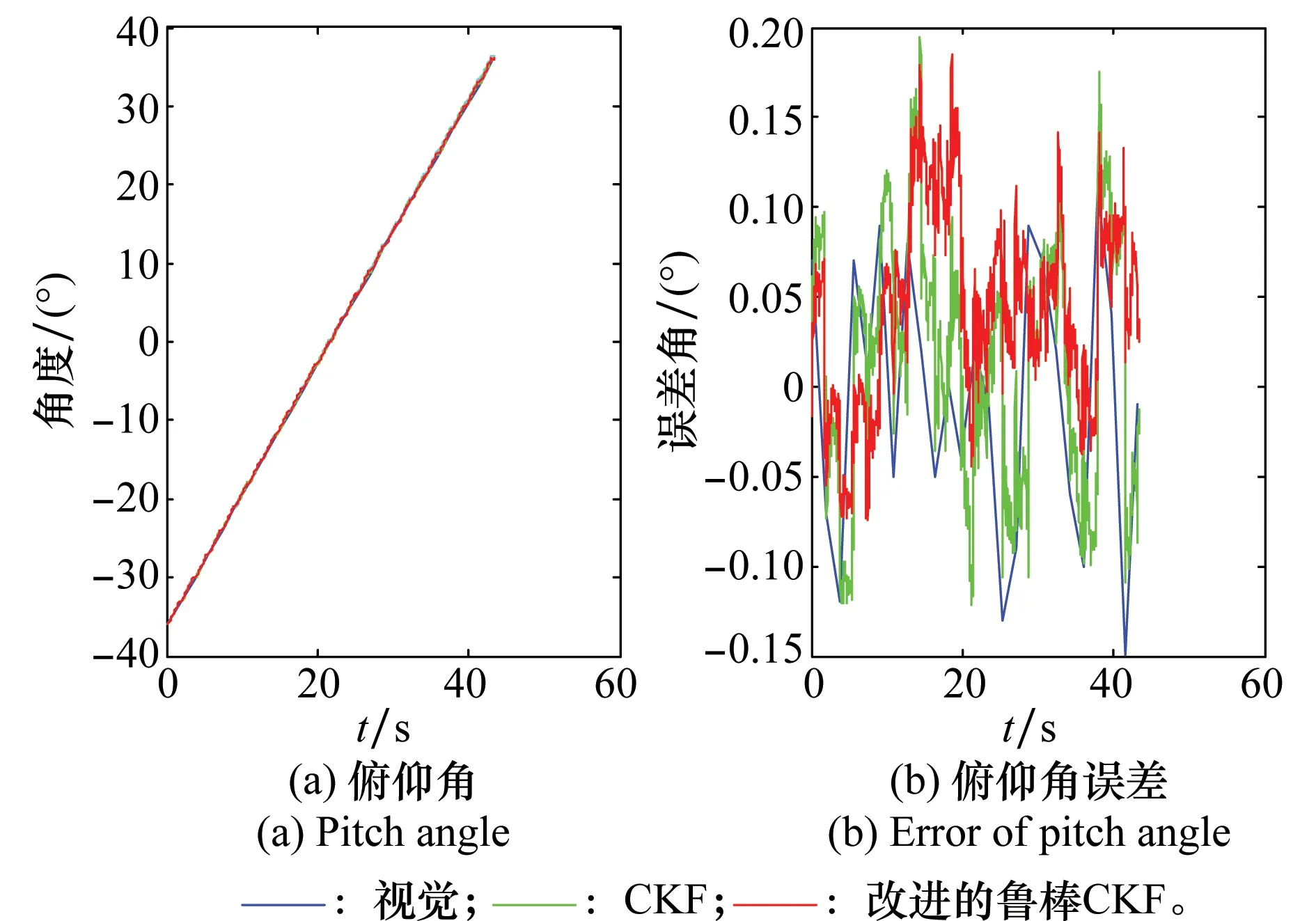
图8 俯仰角-36°～36°运动姿态曲线及对应误差Fig.8 -36°～36°pitch axis attitude curve and its error curve

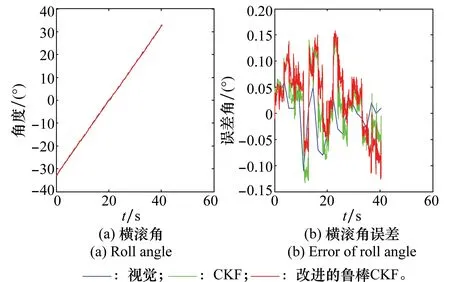
图9 横滚轴-33°～33°运动姿态曲线以及对应误差Fig.9 -33°～33°roll axis attitude curve and its error curve

图10 方位角-48°～48°运动姿态曲线以及对应误差Fig.10 -48°～48°yaw axis attitude curve and its error curve

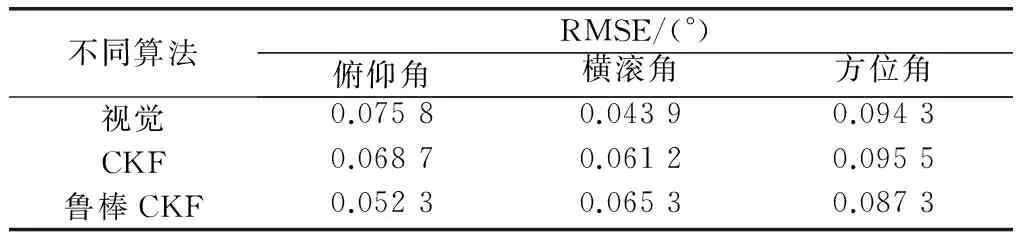
不同算法RMSE/(°)俯仰角横滚角方位角视觉0.07580.04390.0943CKF0.06870.06120.0955鲁棒CKF0.05230.06530.0873

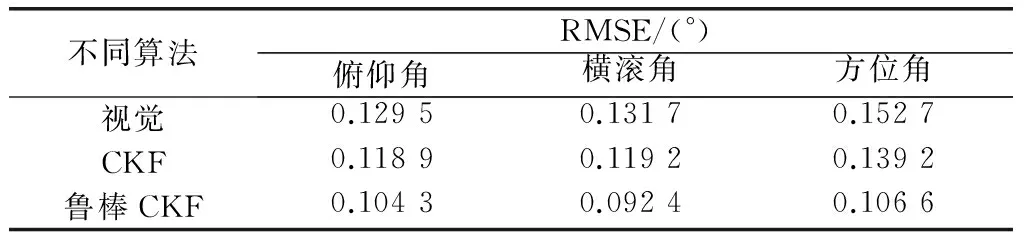
表3 两轴运动不同算法的姿态角RMSE

对图8～图11姿态角误差输出图形进一步分析可知,视觉姿态误差角随时间变化平稳,没有与时间相关的趋势项;但视觉姿态中会存在尖峰噪声,而尖峰噪声的出现是随机的,没有明显的规律。

鲁棒CKF保持与惯性同频率的高频输出且能抑制惯性随时间漂移带来的误差而跟随稳定的视觉姿态。标准CKF也具有高频输出、抑制漂移的特点,但其输出噪声较大无论是视觉的尖峰噪声或惯性的抖动噪声均在标准CKF融合结果中有比较明显的体现,鲁棒CKF在弱化融合结果跟随测量噪声和系统噪声变化方面优于CKF。单轴运动,每个轴的运动时间均不到60 s,其效果表明短时间内鲁棒CKF数据融合算法的有效性;而两轴交替运动,运动时间达到760多秒且运动形式复杂,其效果表明长时间鲁棒CKF数据融合算法的有效性。

为直观说明数据融合后相比纯视觉姿态高频输出的特点,以图8俯仰角单轴运动为例给出融合后数据更新速率与视觉、惯性更新速率的对比,如图13所示。由图13可知,融合姿态可抑制惯性姿态角度漂移,能跟随稳定的视觉姿态,保持惯性数据高频输出的特点。

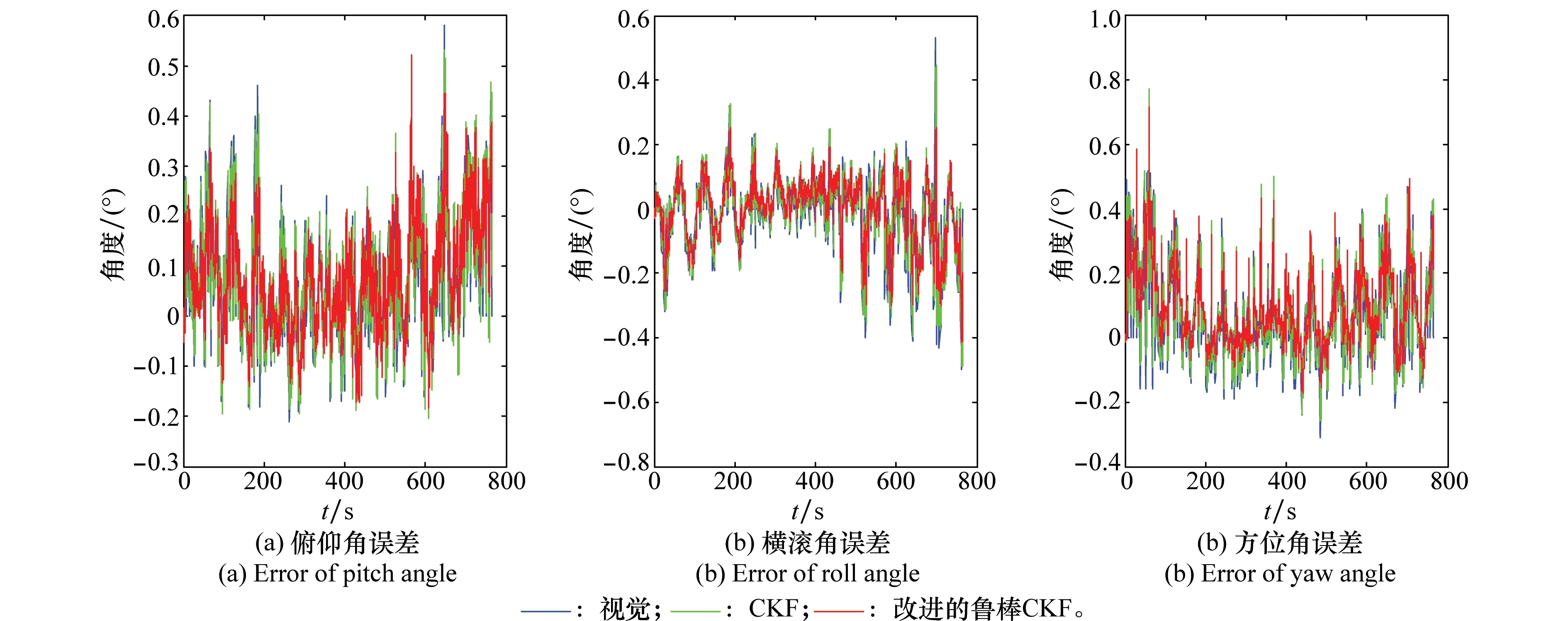
图11 俯仰轴和方位轴交替运动姿态角误差曲线Fig.11 Pitch axis and yaw axis alternating motion attitude angle error curves

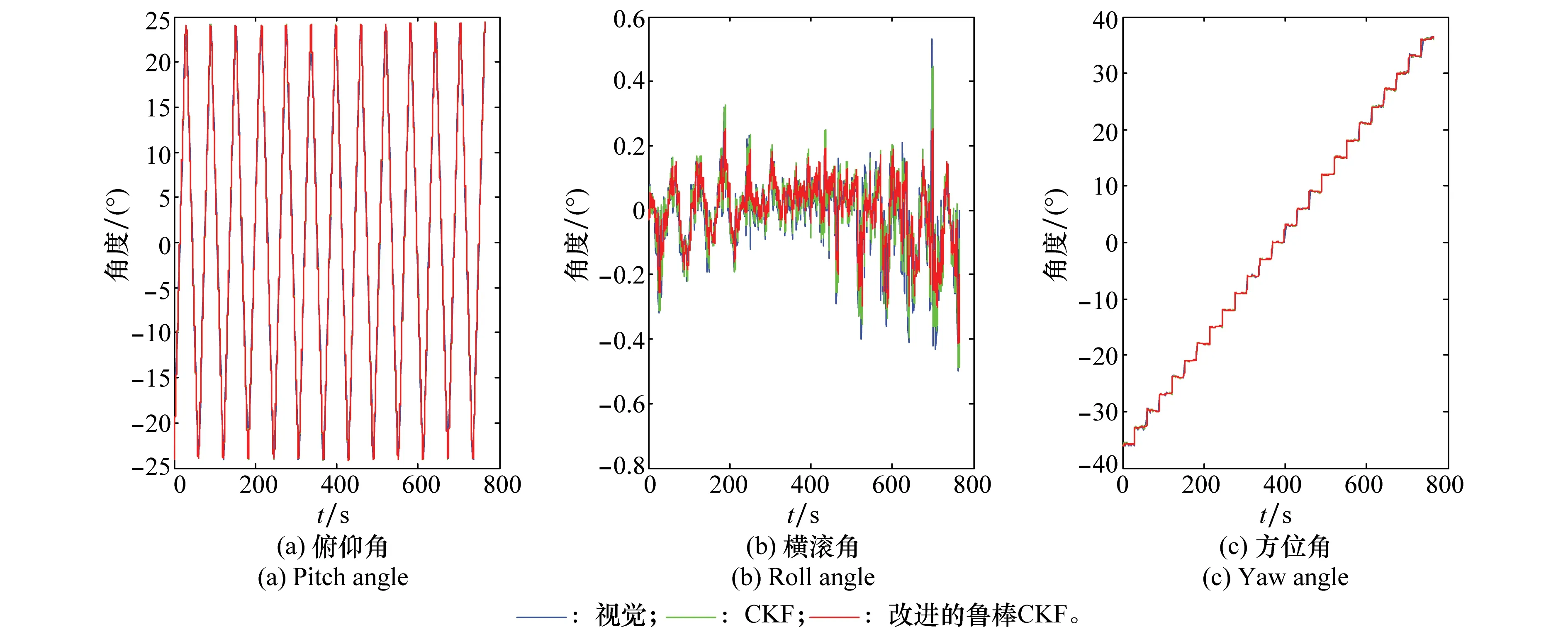
图12 俯仰轴和方位轴交替运动姿态角曲线Fig.12 Pitch axis and yaw axis alternating motion attitude angle curves

图13 融合前后数据更新频率对比Fig.13 Contrast of update frequency before and after data fusion

4 结 论

基于视觉和惯性融合姿态测量的目的,搭建测量系统平台,对测量涉及的坐标系之间的关系进行了梳理和标定,目的是将不同的传感器测量值统一到相同的坐标系中,为进一步的融合计算做准备。运动物体在单轴短时间运动以及双轴长时间运动的不同运动形式中,使用视觉法、惯性法、CKF、矩阵对角化鲁棒CKF法对姿态角进行计算并对姿态误差角进行对比。实验结果表明,鲁棒CKF算法有效地利用视觉测量稳定性好的特性来抑制惯性测量误差随时间无约束发散并结合惯性测量更新频率高的特点,极大地提高融合姿态的输出频率。改进的鲁棒CKF在抑制视觉测量的尖峰噪声、惯性测量的抖动噪声均明显优于CKF滤波算法。使用矩阵对角化变换代替标准CKF算法中的Cholesky分解,可以避免在状态误差协方差矩阵非正定时滤波中断的情况,增加融合滤波算法数值计算的稳定性。

[1] GROVES P D. Principles of GNSS, inertial, and multisensor integrated navigation systems[M]. London:Artech House, 2008.

[2] FOXLIN E. Head-tracking relative to a moving vehicle or simulator platform using differential inertial sensors[C]∥Proc.of the SPIE-International Society for Optical Engineering,2002:133-144.

[3] CARRILLO L R G, LPEZ A E D, LOZANO R, et al. Combining stereo vision and inertial navigation system for a quad-rotor UAV[J].Journal of Intelligent & Robotic Systems,2012,65(1): 373-387.

[4] CHAI L, HOFF W A, VINCENT T. 3-D motion and structure estimation using inertial sensors and computer vision for augmented reality[J]. Presence: Teleoperators and Virtual Environments, 2002, 11(5):474-492.

[5] GEBRE-EGZIABHER D, HAYWARD R C, POWELL J D. Design of multi-sensor attitude determination systems[J]. IEEE Trans.on Aerospace & Electronic Systems,2004,40(2):627-649.

[6] SUN C, SUN P, WANG P. An improvement of pose measurement method using global control points calibration[J]. Plos One, 2015, 10(7): e0133905.

[7] WANG P, XIAO X, ZHANG Z, et al. Study on the position and orientation measurement method with monocular vision system[J]. Chinese Optics Letters, 2010, 8(1): 55-58.

[8] GROVES P D. Navigation using inertial sensors[J]. IEEE Aerospace & Electronic Systems Magazine, 2015, 30(2):42-69.

[9] ENAYATI N. A quaternion-based unscented Kalman filter for robust optical/inertial motion tracking in computer-assisted surgery[J]. IEEE Trans.on Instrumentation & Measurement, 2015, 64(8): 2291-2301.

[10] ZHOU S, FEI F, ZHANG G, et al. 2D human gesture tracking and recognition by the fusion of MEMS inertial and vision sensors[J]. Sensors Journal IEEE, 2014, 14(4):1160-1170.

[11] YANG Z, SHEN S. Monocular visual-inertial state estimation with online initialization and camera-IMU extrinsic calibration[J]. IEEE Trans.on Automation Science & Engineering, 2017,14(1): 39-51.

[12] LIU Y, XIONG R, WANG Y, et al. Stereo visual-inertial odometry with multiple Kalman filters ensemble[J]. IEEE Trans.on Industrial Electronics, 2016, 63(10): 6205-6216.

[13] ARAAR O, AOUF N, VITANOV I. Vision based autonomous landing of multirotor UAV on moving platform[J]. Journal of Intelligent & Robotic Systems, 2016, 85:1-16.

[14] 赵琳,张胜宗,李亮,等.基于自适应EKF的BDS/GPS精密单点定位方法[J].系统工程与电子技术,2016,38(9):2142-2148.

ZHAO L, ZHANG S Z, LI L, et al. BDS/GPS integrated precise point positioning based on adaptive extended Kalamn filter[J]. Systems Engineering and Electronics,2016,38(9):2142-2148.

[15] 乔相伟,周卫东,吉宇人.用四元数状态切换无迹卡尔曼滤波器估计的飞行器姿态[J].控制理论与应用,2012,29(1):97-103.

QIAO X W, ZHOU W D, JI Y R. Aircraft attitude estimation based on quaternion state-switching unscented Kalman filter[J]. Control Theory & Applications, 2012, 29(1): 97-103.

[16] 黄湘远,汤霞清,武萌.基于降维CKF和平滑的SINS/OD动基座对准[J].系统工程与电子技术,2016,38(9):2135-2141.

HUANG X Y, TANG X Q, WU M. Research on moving base initial alignment of SINS/OD with reduced dimension CKF smoo-ther[J]. Systems Engineering and Electronics, 2016, 38(9):2135-2141.

[17] ARASARATNAM I, HAYKIN S. Cubature kalman filters[J]. IEEE Trans.on Automatic Control, 2009, 54(6): 1254-1269.

[18] 张秋昭, 张书毕, 郑南山,等. GPS/INS组合系统的多重渐消鲁棒容积卡尔曼滤波[J]. 中国矿业大学学报, 2014, 43(1):162-168.

ZHANG Q Z, ZHANG S B, ZHENG N S, et al. Multiple fading robust cubature Kalman filter for DPS/INS integrated navigation[J]. Journal of China University of Mining and Technology, 2014, 43(1):162-168.

[19] LIM J. A tutorial-game theory-based extended H infinity filtering approach to nonlinear problems in signal processing[J]. Digital Signal Processing, 2014, 34(1): 1-15.

[20] 赵利强, 陈坤云, 王建林, 等. 基于矩阵对角化变换的高阶容积卡尔曼滤波[J]. 控制与决策, 2016, 31(6): 1080-1086.

ZHAO L Q, CHEN K Y, WANG J L, et al. High-degree cubature Kalman filter based on diagonalization of matrix[J]. Control and Decision,2016, 31(6): 1080-1086.

[21] ZHANG Y, YANG X, XING X, et al. The standing calibration method of MEMS gyro bias for autonomous pedestrian navigation system[J].Journal of Navigation,2016,70(3):607-617.