基于隔离度特性的导引头控制系统优化设计

刘石祥, 杜 肖, 符胜楠, 夏群利

(1. 北京理工大学机电学院, 北京 100081; 2. 中国运载火箭技术研究院, 北京 100076; 3. 北京理工大学宇航学院, 北京 100081)

0 引 言

导引头控制系统不仅要快速跟踪目标,同时还要隔离弹体扰动。隔离度表征了导引头隔离弹体扰动的能力,不仅影响视线角速度的输出精度,同时在制导回路中形成隔离度寄生回路[1-3],影响制导系统的稳定性和制导精度[4-5]。

文献[6]建立了平台导引头隔离度模型。文献[7]利用隔离度简化模型对寄生回路稳定性进行了研究。文献[8]研究平台导引头隔离度对制导系统的影响。为了降低隔离度,很多学者进行了隔离度抑制补偿技术进行研究,文献[9]研究了基于无迹卡尔曼滤波的捷联导引头隔离度补偿方法,文献[10]采用强跟踪无迹卡尔曼滤波对半捷联导引头隔离度进行在线补偿。文献[11]通过估计干扰实现前馈解耦,有效抑制了导引头隔离度。文献[12-13]设计了扰动观测器对弹目视线角速度进行估计并输出到制导系统中,实现对隔离度的抑制。文献[14-15]则是基于干扰力矩模型,对干扰力矩系数进行估计,从而利用干扰力矩模型对视线角速度进行补偿,但是由于估计和补偿算法较为复杂,其所需的估计时间较长。文献[16]指出较宽的稳定回路带宽能够有效降低隔离度,但是导引头稳定回路带宽由于硬件限制不能无限制的增加。文献[17]研究指出,隔离度与导引头回路有重要关系,在导引头稳定回路中引入合适的滞后校正网络可显著提高隔离度水平。

雷达导引头跟踪回路由于受到探测器信号积累所引起的延时的影响,其跟踪回路带宽设计受到限制,一般低于3 Hz,为了保证跟踪高速机动目标,提高导引头跟踪快速性,需要在跟踪回路增加超前校正网络。目前工程上普遍使用的比例-积分-微分(proportional-integral-derivative,PID)或其变形控制器进行校正,其关键的问题就是控制参数的整定[18]。同时为了保证导引头控制系统的频域特性,需要在设计过程中考核导引头的幅值裕度和相位裕度,文献[19]引入了幅值-相位测试器(gain-phase margins tester,GPMT),文献[20]进一步研究了具有时延特性的控制系统参数与频域幅值裕度和相位裕度之间的关系。基于对稳定域的研究,用最大灵敏度函数、误差最小二乘准则等定义目标函数,在所得到的控制参数稳定域利用寻优算法获得控制参数[21]。

本文在保证导引头幅值裕度和相位裕度约束下,通过对内外回路控制系统进行优化设计,使导引头具有更好的隔离度特性和时域特性。首先建立导引头隔离度模型,推导了隔离度传递函数,分析了隔离度与稳定回路和跟踪回路的关系,确定了内外回路分别设计的方法。稳定回路以导引头隔离度指标最优为目标函数,跟踪回路以导引头时域响应最优为目标函数,将幅值裕度和相位裕度转为化对控制参数的稳定域范围,通过分别求解稳定回路和各种回路带约束的优化问题,得到内外回路优化设计参数。通过仿真验证表明,设计的控制系统具有良好的时域特性,同时提高了导引头隔离度,对导引头控制系统设计具有比较大的参考作用。

1 平台导引头隔离度模型

导引头隔离度模型如图1所示。图中G1(s)为导引头跟踪回路前向传函,G2(s)为稳定回路前向传函,包括校正网络和运放,GD(s)为干扰力矩传函,H(s)为速率陀螺传函。该模型包括干扰力矩回路、反电势回路、稳定回路和跟踪回路及电流环回路。稳定回路起到空间稳定作用,跟踪回路起到准确跟踪的作用。干扰力矩回路是由于导引头转动过程中各种导线的拉扯以及转动连接处的动静摩擦等引起的,干扰力矩的产生将会使弹体的运动耦合进导引头运动中,降低导引头的控制精度,对导引头控制是有害的。反电势回路的和电流环一般比较小,对导引头控制精度影响不大。

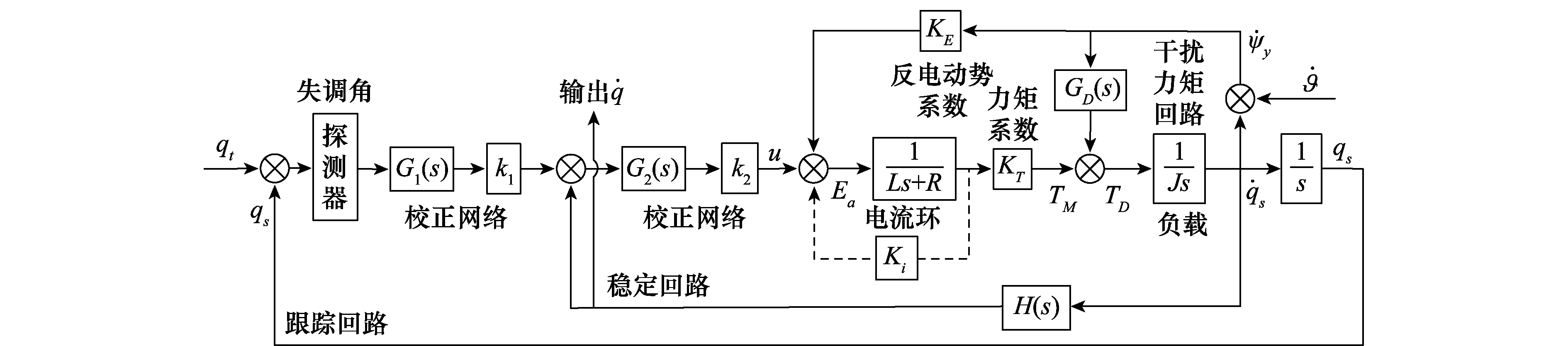
图1 平台导引头隔离度模型Fig.1 Mode of disturbance rejection rate of seeker

平台导引头输出视线角速度,通常既可取自角速率陀螺输出处,又可取自稳定回路的指令输入处,从导引头跟踪的角度来说,由于稳定回路响应速度非常快,所以这两种取法基本可看作一致。但从隔离度的角度分析,这两种取法会造成隔离度传递函数不一致[2]。本文从角速率陀螺处提取视线角速度信号,并建立导引头隔离度模型。

基于传递函数概念给出隔离度传递函数RDRE(s)的定义为

(1)

依图1可以得到导引头隔离度传递函数为

(2)

影响隔离度的干扰力矩主要有弹簧力矩和粘滞阻尼力矩[8]。令弹簧力矩系数为Kn,粘滞阻尼力矩系数为Kω,它们正比于弹簧力矩和粘滞阻尼力矩的大小。把粘滞阻尼力矩模型GD(s)=Kω和弹簧力矩模型GD(s)=Kn/s分别代入式(1)可得到在粘滞阻尼力矩和弹簧力矩作用下隔离度传递函数分别为

(3)

(4)

从式(3)和式(4)可以看出,不同干扰力矩作用下导引头隔离度传递函数不同,导引头隔离度并不能简单认为是某个频点的恒定值,隔离度的频率特性与导引头控制系统的频率特性密切相关。

在对平台导引头隔离度传递函数模型进行等效简化,忽略探测器延时环节及校正网络的影响,令G1(s)=1,G2(s)=1,R≈1,L≈0,稳定回路等效增益K2=G2k2KT/J,跟踪回路等效增益K1=G1k1。对图1做等效变形可得图2。

图2 隔离度等效框图Fig.2 Equivalent block of disturbance rejection rate

干扰力矩为弹簧力矩时,隔离度传递函数如式(5)所示,干扰力矩为阻尼力矩时,隔离度模型如式(6)所示。

(5)

(6)

从式(5)和式(6)可以看出,导引头隔离度水平与导引头回路参数有重要关系,由此可通过改进导引头回路设计达到提高隔离度水平的目标。

导引头跟踪回路带宽决定了导引头跟踪的快速性,而由于探测器延时的存在及噪声的影响等硬件制约,导引头的快速性与稳定性成了相互制约的关系,跟踪回路带宽一般限制在3 Hz以下,典型值取2 Hz。而导引头稳定回路带宽决定了其抗弹体扰动的能力,内回路带宽越大隔离度特性越好,其带宽受到电机、角速率陀螺等动力学的影响,一般可设计至30 Hz以上,远大于导引头跟踪回路带宽,从而使得导引头控制系统内外回路之间的影响较小,可以实现导引头内外回路分开设计。

2 导引头优化设计流程

2.1 频域指标约束

对于一个典型的单输入单输出(single input single output,SISO)单位反馈控制系统,进行控制系统设计时需要满足期望的频域指标,假设A为系统的幅值裕度,φ为系统相位裕度,在求取SISO控制系统满足频域约束的稳定域时,可借助如图3的带有GPMT[21]的控制系统结构图求解。

图3 带有GPMT的控制系统结构Fig.3 Block of control system with GPMT

当A=1,φ为期望的相位裕度,则图3所示系统的稳定性设计可转变为基于相位裕度的控制参数设计;当φ=0,A为期望的幅值裕度,则图3所示系统的稳定性设计可转变为基于幅值裕度的控制参数设计;求取两者的交集即可获得基于幅值裕度和相位裕度约束的稳定域。

2.2 目标函数

幅值裕度和相位裕度是控制系统稳定性的衡量指标,在控制系统设计时,还应该导引头抗弹体扰动能力的隔离度指标和跟踪能力的时域响应指标,针对这两个指标设计目标进行控制系统参数优化。

(1) 隔离度目标函数

根据工程实践和研究[17],稳定回路增益与弹体隔离度成反比关系,通过增大稳定回路增益,可以降低导引头隔离度。选取导引头频率ωa处的稳定回路开环增益最大为目标函数,使其幅值最大,则可得到当前条件下的最小隔离度。

选取稳定回路目标函数为

J=M(ωa)

(7)

用D来表示基于幅值和相位裕度约束的稳定区域,选取典型的导引头频率ωa=2 Hz,则约束优化问题可以描述为

(8)

(2) 时域目标函数

跟踪回路增益对隔离度的影响比较小,主要衡量其跟踪能力,通过时域目标函数来实现跟踪回路优化。时域目标函数分为特征型目标函数和误差型目标函数两大类。误差型目标函数采用期望响应和实际响应之差的某种表达式作为目标函数。常用的误差型目标函数包括误误差平方矩的积分型(integrated time square error,ITSE)、误差平方的积分型(integrated square error,ISE)、误差绝对值矩的积分型(integrated time absolute error,ITAE)和误差绝对值的积分型(integrated absolute error,IAE)。

2.3 设计流程

在求解有约束最优化问题时,可通过构造惩罚函数等方法将有约束的优化问题转换为无约束优化问题从而进行求解,也可基于KKT(Karush-Kuhn-Tucker)方程解的方法进行求解。一般地,最优化数学模型能够表示成下列标准形式:

(9)

表1 Etime目标函数

为了实现有约束条件下的最优值求解,要求约束的梯度向量与目标函数的梯度向量在最优解处平行。KKT算法利用拉格朗日法合并目标函数与约束,并通过求取如式(9)所示不等式组最小值点x*获得有约束条件下的最优值。故而基于KKT法的一般约束优化问题极值点一阶必要条件可表示为

(10)

式中,μi和λi为拉格朗日乘子。KKT方程是有约束优化问题的必要条件,KKT方程的解形成了许多非线性规划算法的基础,这些算法直接计算拉格朗日乘子,通过用拟牛顿法更新过程,给KKT方程积累二阶信息,可以保证有约束拟牛顿法的超线性收敛。基于KKT方法的Fmincon函数可用于有约束非线性优化问题,可先通过Simulink搭建控制系统框图,再利用Fmicon函数进行寻优算法。基于上述分析,导引头优化设计流程图如图4所示。

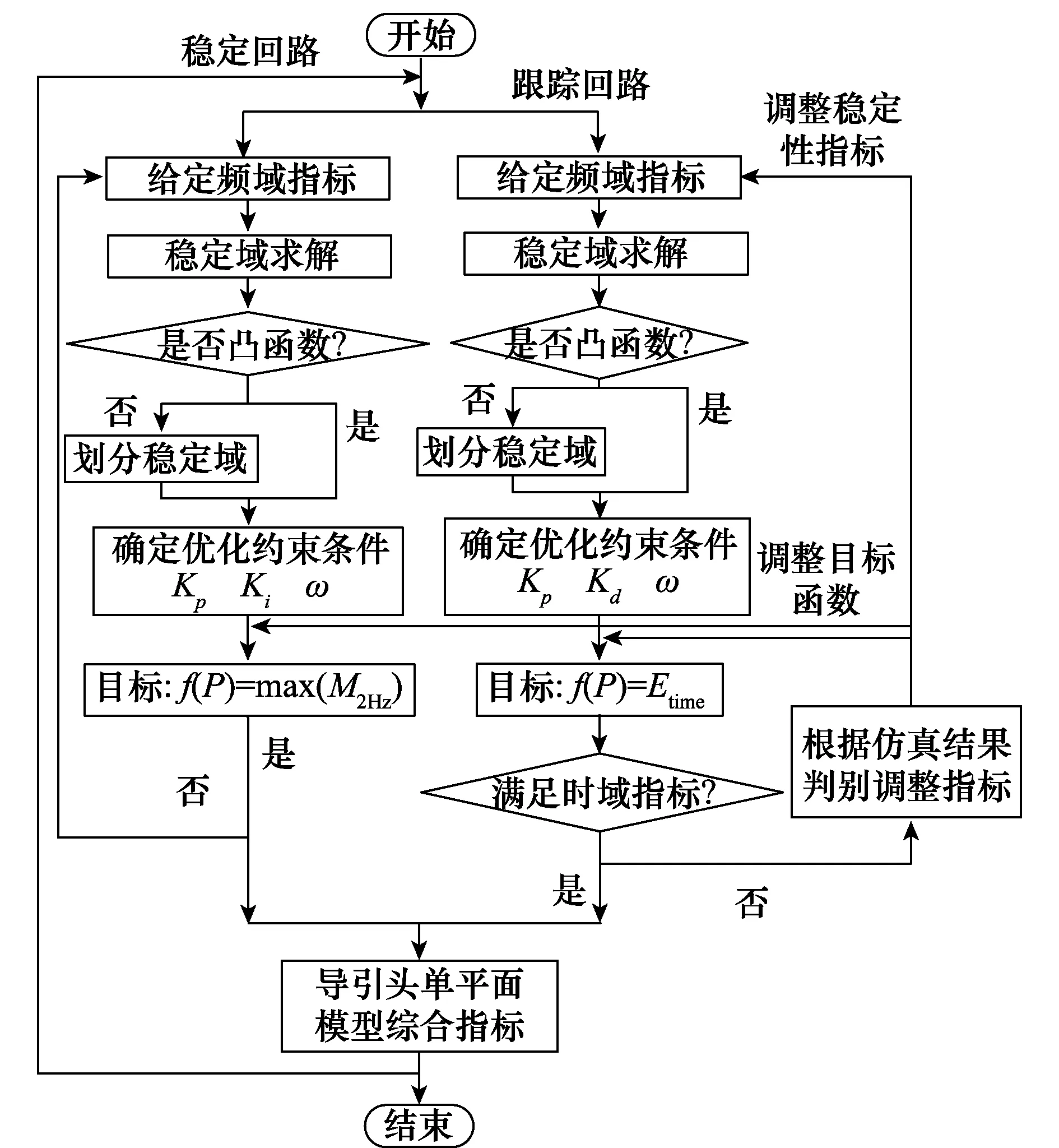
图4 优化设计流程Fig.4 Optimization design process

3 导引头稳定回路设计

稳定回路以关心频率点处隔离最小为控制系统的优化目标函数,以控制系统幅值和相位裕度作为约束条件,采用PI校正网络进行稳定回路控制系统设计,提高稳定回路中关心频带的增益,从而降低导引头隔离度幅值。经过简化得稳定回路框图如图5所示。

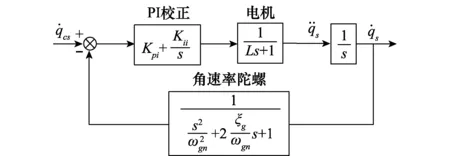
图5 稳定回路框图Fig.5 Stabilized loop block diagram

采用GPMT方法[21],鉴相环节为Ae-jφ,则可得到带有GPMT的稳定回路框图，如图6所示。

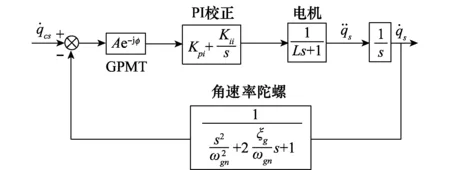
图6 带有GPMT的稳定回路框图Fig.6 Stabilized loop block diagram with GPMT

稳定回路开环传递函数为

(11)

则稳定回路的闭环特征方程为

Ae-jφ×(Kpis+Kii)

(12)

根据线性系统判稳条件,闭环系统特征根均在左半平面,相当于式(12)无右半平面根。令s=jω,并代入式(12),并采用欧拉公式,则可获得如式(13)所示的基于实部和虚部的特征方程表达式:

F(ω)=Fr(ω)+jFi(ω)

(13)

其实部和虚部分别表示为

(14)

可得如(15)所示的边界条件。

(15)

故而,闭环特征方程的稳定性可以在控制参数空间(Kp,Ki)进行研究,则求解方程组(15),可得控制参数表达式为

(16)

式中

解方程组可以得到曲线(Kpi(ω),Kii(ω)),从而形成分割控制参数空间的稳定边界如图7所示,取角速率陀螺参数ωgn=80 Hz，ξg=0.7 。

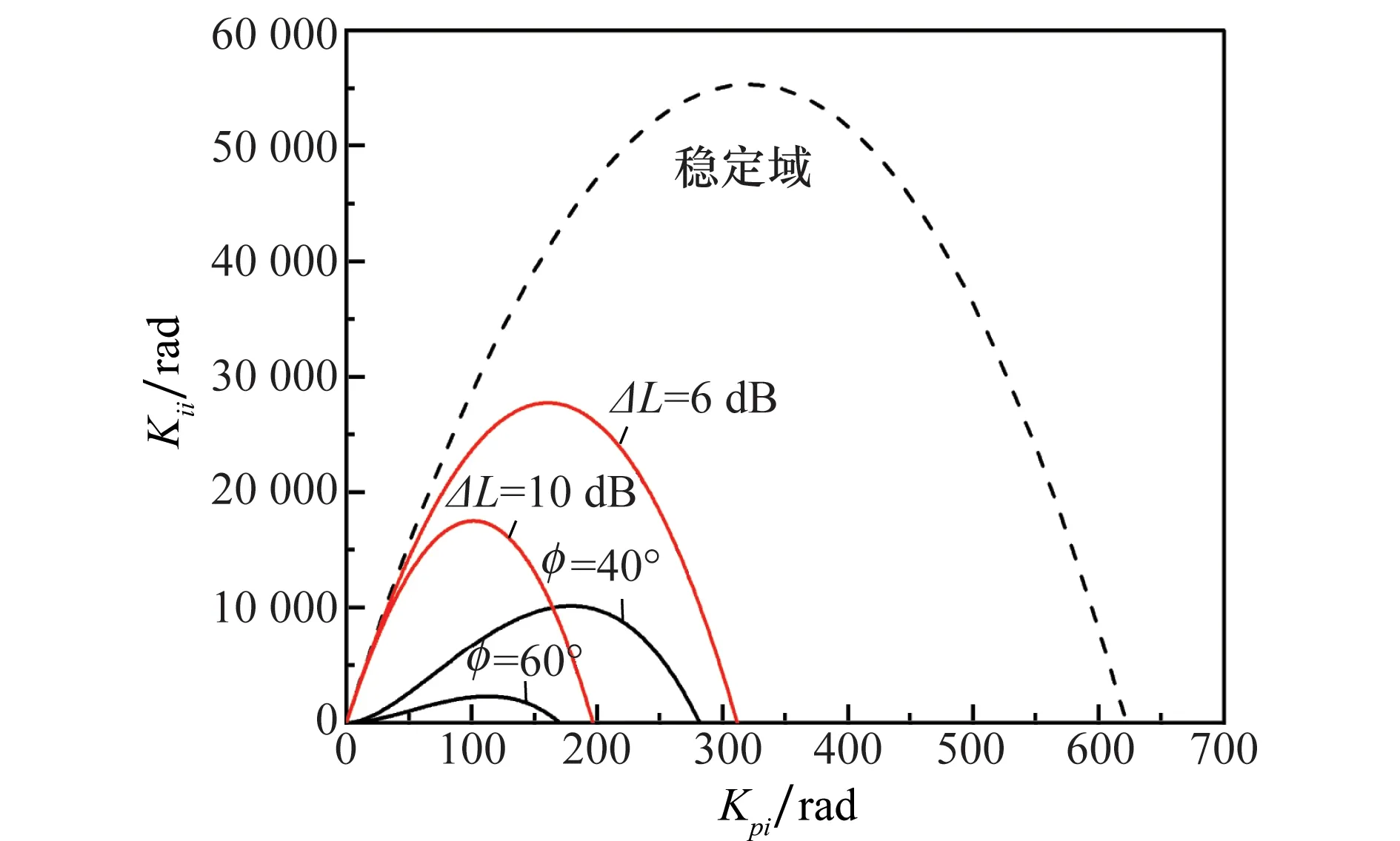
图7 不同幅相裕度条件下稳定域分布Fig.7 Stability region under different amplitude margin and phase margin

幅稳定裕度ΔL=6 dB,相稳定裕度条件φ=40°,同时满足幅值和相位裕度约束时,Kpi和Kii的取值范围为相角裕度φ=40°形成的边界线,故而控制参数稳定域可表示为

D={Kpi(φ=40),Kii(φ=40)}

(17)

根据式(8)所示稳定回路目标函数,约束优化问题可以表示为

(18)

由图8可知,2 Hz点幅值的极大值分布于稳定域边界处,从而形成凸函数,有利于优化方法的使用,通过求解其极小值,获得最优解为Kpi=181,Kii=1.0×104。

图9 有无PI校正稳定回路开环伯德图Fig.9 Compare of open loop Bodes for stabilized loop with PI compensator and no compensator

采用最优控制参数获得如图9所示有无PI校正稳定回路开环伯德图对比。无PI校正时2 Hz点增益为22.2,采用基于幅相裕度约束的最优化控制参数时2Hz处增益为65.4,比之前提高了3倍,则隔离度水平提高3倍。

4 导引头跟踪回路设计

跟踪回路以探测器跟踪误差角最小为目标函数,以控制系统幅值相裕度作为约束条件,采用PD校正网络,实现快速跟踪目标,在保证较小超调量的同时响应时间尽量短。探测器纯延时取为40 ms,跟踪回路校正网络设计时的幅相裕度,依然采用GPMT法,如图10所示。

图10 有GPMT的跟踪回路框图Fig.10 Tracking loop block diagram with GPMT

此时,跟踪回路开环传递函数为

(19)

则跟踪回路的闭环特征方程为

(20)

利用欧拉公式,式(20)可表述为式(21)所示实部与虚部的形式。

F(jω)=Fr(ω)+jFi(ω)

(21)

其中,Fr(ω)为实部;Fi(ω)为虚部。求解

(22)

可得

(23)

式中

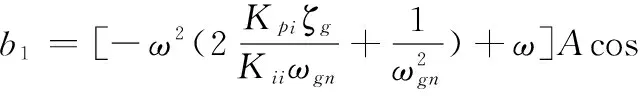
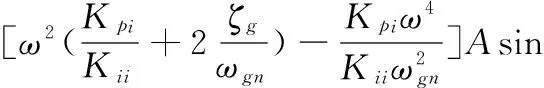
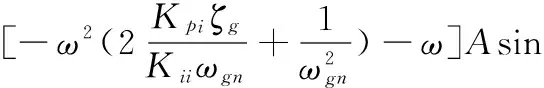
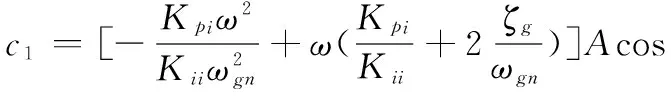
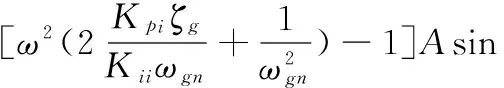
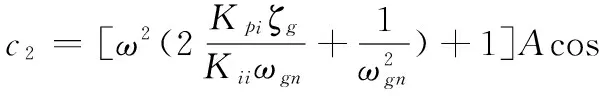
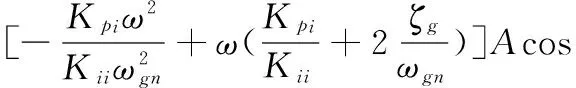
在此控制方案中,有一个微分控制器位于前向通路,另一个微分控制器位于反馈通路,将稳定回路的微分因素分配在前向通道上可以:①改善跟踪回路的稳定裕度,在一定程度上提高跟踪回路的带宽;②在稳定回路特性一定的条件下改善导引头的隔离度特性。故而可得到其稳定域的分布如图11所示。

由图11可知,由于导引头跟踪回路受到导引头探测器信息处理延时的影响,其幅裕度对控制参数Kpo和Kdo较为敏感,而相裕度次之,故而幅裕度6 dB稳定边界位于相裕度40°稳定域范围之内,在后续对控制参数进行寻优时,可将约束条件设置为幅裕度6 dB。在满足幅裕度的稳定边界处随着Kpo的不同,其时域特性具有明显的差异,Kpo越大其超调量越大。

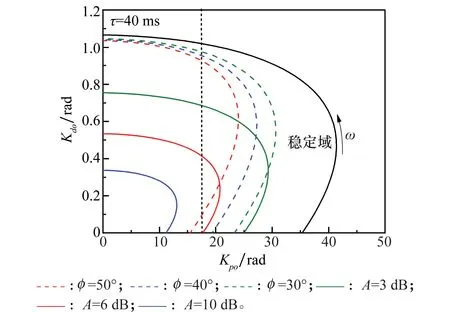
图11 PD校正稳定域分析图Fig.11 Analysis of stabilized region with PD

由目标函数等高线与稳定域的边界可知,如图12所示,控制系统参数最优点位于约束边界与目标函数等高线相切处;当目标函数极值点位于稳定边界以内,则控制参数最优点与约束边界无关。

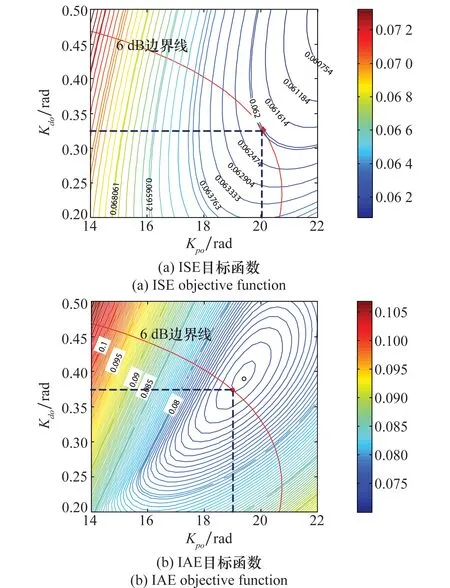
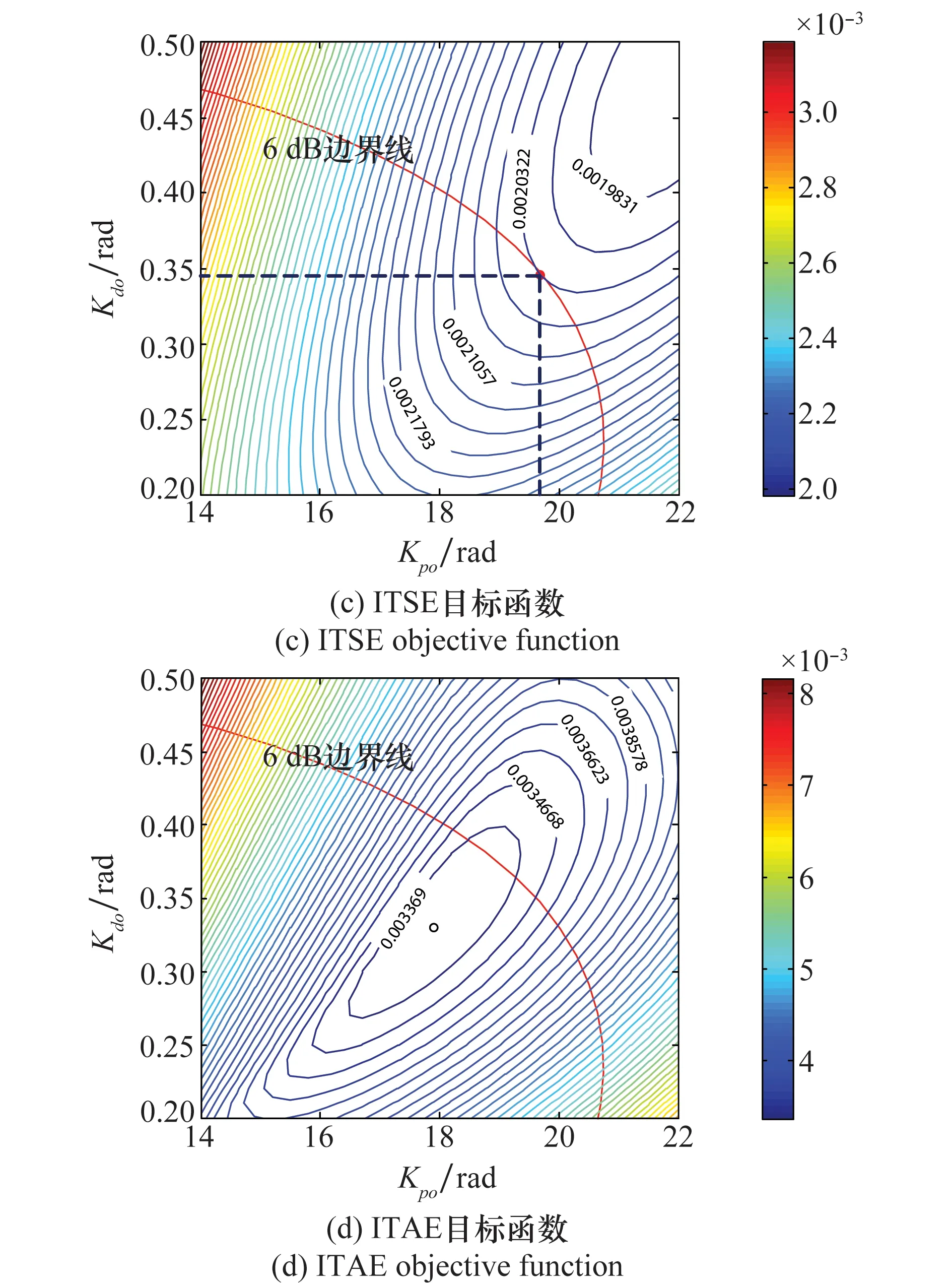
图12 时域目标函数等高线图Fig.12 Contour map of time domain objective functions

图13为满足稳定域的时域目标函数优化结果,从分布上可以看出,不同目标函数准则下的最优点基本都在稳定边界上,满足稳定性要求,如果进一步放开稳定裕度要求,则可得到更好的时域性能指标。

图13 稳定域分布Fig.13 Stability region

5 导引头控制系统仿真验证

根据设计的稳定回路和跟踪回路优化设计参数,代入导引头控制系统中,进行导引头时域性能和隔离度特性仿真验证。导引头控制系统框图如图14所示。

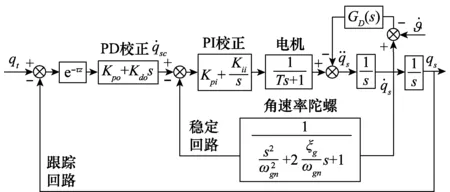
图14 具有校正网络导引头控制系统Fig.14 Seeker control system with correction network

导引头跟踪时域特性仿真结果如图15所示。从图15可以看出,未进行超前校正时阶跃响应具有比较大的超调,通过优化控制设计,降低了超调,ITAE准则下的超调最小。

图15 导引头时域特性Fig.15 Time domain characteristic of seeker

各准则时域优化时的结果分布较为集中,各优化结果的性能指标如表2所示。

表2 时域特性优化对比

导引头隔离度特性仿真结果如图16和图17所示。仿真结果表明,采用校正网络后隔离度水平提高了3倍,同时校正网络的存在对隔离度的相位产生影响。通过对比分析可知,外回路设计指标采用不同误差准则作为目标函数对隔离度影响不大,故而在后续的控制系统设计时可根据具体时域要求进行设计,而主要通过内回路设计采用隔离度的目标函数进行约束,以最大程度提高隔离度水平。

该抑制隔离度的方法通过建立以失稳频率点处隔离最小为控制系统的优化目标函数,以控制系统幅相裕度作为约束条件,综合考虑导引内外回路进行设计,能够在保证控制系统频域指标的同时,提高隔离水平。但是该方法由于受到控制系统设计的约束,对于隔离度水平的提高受到一定的限制。

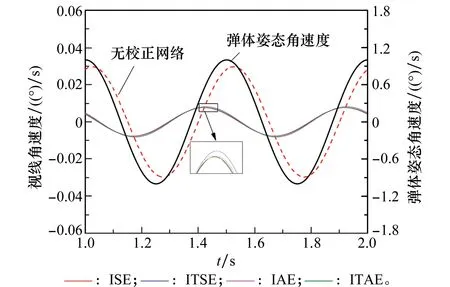
图16 弹簧力矩隔离度Fig.16 Disturbance rejection rate caused by spring torque

图17 阻尼力矩隔离度Fig.17 Disturbance rejection rate caused by damping moment

6 结 论

为了改进导引头跟踪度特性和时域特性,通过对带导引头内外回路带宽与导引头时域性能分析,提出了一种保证幅值裕度和相位裕度约束条件下进行内外回路优化设计的方法,稳定回路以导引头隔离度指标最优为目标函数,跟踪回路以导引头时域响应最优为目标函数,并对设计结果进行了仿真验证,得到结论如下:

(1) 导引头隔离度与稳定回路增益有重要关系,在保证稳定回路稳定裕度的条件下,提高稳定回路增益可以提高导引头隔离度;

(2) 基于隔离度特性的导引头控制系统优化设计,既保证了导引头幅值裕度和相位裕度要求,也使系统具有较好的鲁棒性;

(3) 通过内外回路优化设计,提高了导引头隔离度水平,导引头也具有较好的时域特性。但由于控制系统设计约束,导引头隔离度水平的提高受到限制。

以上结论表明,基于隔离度特性的导引头控制系统优化设计对平台导引头控制系统设计具有重要参考作用。

[1] 鄢琴涛,李娜,鲁天宇,等.导引头隔离度机理及其寄生回路频域影响分析[J].弹箭与制导学报, 2016, 36(2): 43-51.

YAN Q T, LI N, LU T Y, et al. Research on disturbance rejection rate mechanism of seeker and frequency domain analysis for parasitic loop[J]. Journal of Projectiles Rockets Missiles and Guidance, 2016, 36(2): 43-51.

[2] 李富贵,夏群利,崔晓曦,等.导引头隔离度寄生回路对视线角速度提取的影响[J].宇航学报, 2013, 34(8): 1072-1077.

LI F G, XIA Q L, CUI X X, et al. Effect of seeker disturbance rejection rate parasitic loop on line of sight rate extraction[J]. Journal of Astronautics, 2013, 34(8): 1072-1077.

[3] KWON Y S, HWANG H Y, CHOI Y S. Stabilization loop design on direct drive gimbaled platform with low stiffness and heavy inertia[C]∥Proc.of the IEEE International Conference on Control, Automation and Systems, 2007: 320-325.

[4] 李富贵,夏群利,祁载康.导引头隔离度寄生回路对最优制导律性能的影响[J].航空学报, 2013, 34(12): 2658-2667.

LI F G, XIA Q L, QI Z K. Effect of seeker disturbance rejection rate parasitic loop on performance of optimal guidance law[J]. Acta Aeronautica et Astronautica Sinica,2013,34(12):2658-2667.

[5] SONG J M, CAI G H, KONG L X, et al. Precision analysis of the semi-strapdown homing guided system[J].Journal of Aerospace Engineering,2014,27(1):151-167.

[6] 崔莹莹,夏群力,祁载康.导引头稳定平台隔离度模型研究[J].弹箭与制导学报, 2006, 26(1): 22-25.

CUI Y Y, XIA Q L, QI Z K. Seeker platform disturbance rejection mathematical model[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006, 26(1): 22-25.

[7] 杜运理,夏群利,祁载康.导引头隔离度相位滞后对寄生回路稳定性影响研究[J].兵工学报,2011,32(1): 28-32.

DU Y L, XIA Q L, QI Z K. Research on effect of seeker disturbance rejection rate with phase lag on stability of parasitical loop[J]. Acta Armamentarii, 2011, 32(1): 28-32.

[8] 宋韬,林德福,王江.平台导引头隔离度对导弹制导系统影响[J].哈尔滨工程大学学报, 2013, 34(10): 1234-1241.

SONG T, LIN D F, WANG J. Influence of seeker disturbance rejection rate on missile guidance system[J]. Journal of Harbin Engineering University, 2013, 34(10): 1234-1241.

[9] 宗睿,林德福,王伟,等.基于多模型的捷联红外导引头隔离度在线补偿方法[J].系统工程与电子技术, 2017, 39(1):147-155.

ZONG R, LIN D F, WANG W, et al. Multiple mode based on-line compensation for disturbance rejection rate of strapdown infrared seeker[J]. Systems Engineering and Electronics, 2017, 39(1):147-155.

[10] 胡欧磊,王江,黄鹏,等.半捷联导引头隔离度影响与STUKF在线补偿[J].红外与激光工程, 2017, 46(3): 158-167.

HU O L, WANG J, HUANG P, et al. Effect of disturbance rejection rate on semi-strapdown seeker and on-line compensation of STUKF[J].Infrared and Laser Engineering, 2017, 46(3): 158-167.

[11] ABHINJT B R N B. Performance analysis of nominal scheme and decoupling loop scheme for RF seeker[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference and Exhibit, 2002.

[12] 徐娇,王江,宋韬,等.基于扰动观测器的导引头隔离度抑制方法研究[J].兵工学报, 2014, 35(11): 1790-1798.

XU J, WANG J, SONG T, et al. A disturbance observer-based inhibition method for disturbance rejection rate of seeker[J]. Acta Armamentarii, 2014, 35(11): 1790-1798.

[13] SONG T, LIN D F, WANG J. Disturbance observer-based control for missile non-strapdown seeker disturbance rejection[J]. Advances in Mechanical Engineering, 2016, 8(4): 1-15.

[14] YU S, ZHAO Y Z. Simulation study on a friction compensation method for the inertial platform based on the disturbance observer[J]. Proceedings of the Institution of Mechanical Engineers Part G-Journal of Aerospace Engineering, 2008, 222(3): 341-346.

[15] LIN C L, HSIAO Y H. Adaptive feedforward control for disturbance torque rejection in seeker stabilizing loop[J]. IEEE Trans.on Control Systems Technology,2001,9(1): 108-121.

[16] MASTEN K M. Applications of control theory to design of line-of-sight stabilization system[C]∥Proc.of the American Control Conference, 1985:1219-1222.

[17] 李富贵,夏群利,蔡春涛,等.导引头隔离度对寄生回路稳定性的影响[J].红外与激光工程, 2013, 42(9): 2341-2347.

LI F G, XIA Q L, CAI C T, et al. Effect of seeker disturbance rejection rate on parasitical loop stability[J]. Infrared and Laser Engineering, 2013, 42(9): 2341-2347.

[18] TOSCANO R. A simple robust PI/PID controller design via numerical optimization approach[J]. Journal of Process Control,2005,15(1):81-88.

[19] CHANG C H, HAN K W. Gain margins and phase margins for control systems with adjustable parameters[J]. Journal of Guidance, 1990, 13(3): 404-408

[20] WANG Y J. Graphical computation of gain and phase margin specifications-oriented robust PID controllers for uncertain system with time-varying delay[J]. Journal of process Control, 2011, 21(4): 475-488.

[21] 欧林林,顾诞英,张卫东.基于幅值裕度和相位裕度的PID参数最优整定方法[J]. 控制理论与应用, 2007, 24(5):837-840.

OU L L, GU D Y, ZHANG W D. Optimal tuning method of PID controller based on gain margin and phase margin[J]. Control Theory & Applications, 2007, 24(5):837-840.