基于ESO的无人直升机轨迹鲁棒跟踪控制

陈南宇, 黄 俊, 周尧明, 赵文龙

(北京航空航天大学航空科学与工程学院, 北京 100083)

0 引 言

无人直升机具有悬停、侧飞、倒飞、低速巡航等独特的飞行特性,在侦察、救援、航拍、植保等军/民用领域引起了人们的广泛关注。然而,无人直升机是一种强耦合、静不稳定、欠驱动的高阶的非线性系统,并且时刻暴露在多扰动的环境中,设计一种简单而实用的无人直升机飞行控制系统是一项颇具挑战性的任务。

近年来,国内外的专家学者为无人直升机设计了许多线性和非线性的控制方法,例如PID控制[1]、增益调度控制[2]、H∞回路成形控制[3]、线性二次型方法[4]、反馈线性化方法[5]、自适应滑模控制[6]、预测控制[7]、动态逆[8]、反步法[9]等。但是,线性控制方法仅能在平衡点附近发挥效果,故不适用于本质上包含强非线性特性、系统参数时变的无人直升机控制系统。而另一方面,非线性控制在实际飞行中效果也差强人意,达不到实用化要求,主要原因是无人直升机系统常常存在很多不确定性,例如测量噪声、外部扰动、建模误差、控制器死区和饱和以及控制器与所要控制的系统之间存在的不可直接测量的输入未建模动态等,它们都是影响系统飞行性能的不利因素。无人直升机的控制问题就是系统不确定性的处理问题或抗扰问题[10]。

自适应控制是处理不确定非线性系统的一种有效方法,它与反步法相结合被广泛应用于无人直升机飞行控制器的设计当中。文献[11]利用分层控制策略研究了模型直升机的轨迹跟踪控制方法,在外回路中设计了基于积分二次型李雅普诺夫函数的位置控制器,内回路设计了一种无奇异姿态控制律实现了姿态跟踪,并通过自适应律对未建模动态进行估计和补偿。文献[12]利用自适应反步法研究了具有惯性参数不确定性的微型直升机的轨迹跟踪问题,该算法在简化的级联形式的直升机模型基础上采用反步法设计控制器,通过自适应更新律对惯性参数不确定性进行在线补偿。文献[13]给出了基于L1自适应控制与非线性前馈控制方法补偿相结合的四旋翼飞行器轨迹跟踪控制器,对飞行过程中时变气动作用和有界外部干扰进行处理,实现了对于任何给定有界参考轨迹输出信号的渐近跟踪。文献[14]也利用自适应反步法和非线性自适应律获得了无人直升机轨迹的鲁棒跟踪控制,通过将干扰估计值整合到反步控制器中, 使得闭环跟踪系统的鲁棒稳定性得到保证,并证明了所设计的控制器对干扰具有主动阻隔效果。

以上方法通过在线辨识或直接对摄动参数进行调整,实现对变化的自适应,并利用反步法实现整个系统的稳定性。但是,随着研究的深入,人们发现单纯的自适应控制对于系统外部干扰和未建模动态非常敏感,可能导致参数漂移等现象的发生[15]。因此,若能采用一种方法或策略,能够降低或消除这些外部干扰和未建模动态的影响,那么参数漂移也将得到有效抑制。而扩张状态观测器(extended state observer, ESO)正是解决这一问题的一种可行方法。ESO是文献[16]提出的自抗扰控制技术的核心,其基本思想是:将各种耦合作用、未建模动态以及外部扰动看成综合扰动进行实时估计,然后利用估计输出设计补偿控制律来提高已有控制器的控制性能,从而达到消除扰动的目的。扩张状态观测器为自适应控制参数漂移问题提供了天然的解决途径。因此,将两者结合起来用于模型失配、参数摄动以及环境干扰等多种扰动类型并存情形下的无人直升机飞行控制器的设计,将有助于进一步保持和发挥自适应反步法的优点,提高系统的鲁棒性能。

本文针对无人直升机不确定性问题,综合考虑惯性参数摄动、未建模动态以及外界未知干扰等各种不确定性的综合影响,提出了一种将扩张状态观测器和自适应反步控制相结合的无人直升机鲁棒控制方法,以增强飞行控制系统的抗干扰性和对时变参数的自适应性。其中,利用ESO实现系统未建模动态以及外界未知有界干扰的实时估计和在线补偿,利用自适应律实现对时变惯性参数的动态调整。最后,通过对上升螺旋线的轨迹跟踪,验证了所设计控制器的有效性。

1 系统模型

1.1 机身动力学模型

将无人直升机机身视为刚体,其机身动力学模型[17]为

(1)

(2)

(3)

(4)

(5)

式中,Cθ,Sθ及Tθ分别表示cosθ,sinθ和tanθ的简写,其他类推。为了保证H不会出现奇异性,假定θ≠±π/2。R∈SO(3)为机体坐标系到惯性坐标系的旋转矩阵,其表达式为

(6)

J∈R3×3表示无人直升机的惯性矩阵,由于无人直升机关于机体坐标系x-z平面对称,因此惯性矩阵J可表示为

(7)

式中,Ixx,Iyy,Izz和Ixz为转动惯量。

1.2 力和力矩计算

若Fmr和Ftr分别表示机体系下主旋翼和尾桨作用在机身上的空气动力向量,则

(8)

Ftr=[0Ytr0]T=[0 -Ttr0]T

(9)

因此,作用在无人直升机机身上的合外力为

(10)

若记(lmr,ymr,hmr)和(ltr,ytr,htr)分别为机体坐标系下主旋翼桨毂中心及尾桨轴相对直升机质心的位置,则无人直升机机身上的总外力矩为

(11)

主旋翼和尾桨产生的拉力Tmr和Ttr,可近似采用如下计算公式(i=mr,tr)[18]：

Ti=CTi·ρ(ΩiRi)2Ai/2

(12)

(13)

主旋翼和尾桨旋转产生的扭矩Qmr和Qtr可表示为

Qi=CQi·ρ(ΩiRi)2AiRi/2

(14)

(15)

1.3 旋翼一阶挥舞动态

主旋翼挥舞角影响无人直升机机身受力和力矩,纵向挥舞β1c与横向挥舞角β1s分别由纵向周期变距θ1c和横向周期变距θ1s控制。基于文献[19],本文忽略挥舞动态二阶量,整理、合并后得到主旋翼挥舞运动一阶动态为

(16)

式中

B1=[β1c,β1s]T,θ1=[θ1c,θ1s]T,ω12=[p,q]T

R(β)表示主旋翼桨毂坐标系到气流坐标系的旋转矩阵,其表达式为

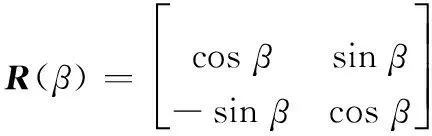
(17)

式中,β为侧滑角。其他符号含义详见文献[19]。

2 模型等效变换

无人直升机力和力矩主要由主旋翼和尾桨旋转产生的,利用文献[20]的简化方法,可将式(2)变形为

(18)

式中,d1表示忽略机身、平尾、垂尾气动力而带来的模型简化误差以及未建模动态的总和。

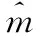
(19)

(20)

式中

旋翼挥舞是旋翼系统的独有特征,是无人直机动力学特性的重要组成部分,在控制器设计时应该加以考虑,但已有文献常常加以忽略。文献[14]考虑了旋翼挥舞动态,但只是将其简化成一种稳态过程,本质上并未反映无人直升机的动态特征。因此,本文将采用一阶挥舞动态,将其与无人直升机的姿态动力学方程进行整合,推导出耦合了旋翼挥舞动态的扩张姿态动力学方程。

首先,对式(11)进行等价变形,可得

τb=QAU+QB+d2

(21)

式中,d2表示忽略平尾、垂尾等力矩而带来的建模误差总和;QA、QB和U分别为

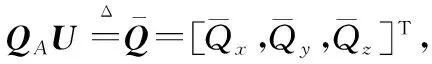
(22)

将式(22)代入式(21),并利用式(12)、式(13)尾桨拉力计算公式,可将式(21)变换为

(23)

式中,θtr表示尾桨总距;f3为机体坐标系ZB轴变换过程中剩余项及建模误差等的总和;系数R3表达式为

(24)

对式(22)两边求时间导数,并将式(16)旋翼挥舞动态代入,整理可得

(25)

式中,θ1=[θ1c,θ1s]T为主旋翼纵向/横向周期变距向量;f12表示机体坐标系XB、YB轴等效变换过程剩余项及建模误差等的总和;R12表达式为

R12=QA12Kθ

(26)

至此,推导得到了耦合旋翼挥舞动态的无人直升机系统模型,它由位置子系统和扩张的姿态子系统组成,分别为

(27)

(28)

3 ESO设计

3.1 位置动力学方程ESO设计

根据式(19),对无人直升机位置动力学方程设计扩张状态观测器,用以在线估计d1,则

(29)

式中

通过以上观测,可得z1→V,z2→d1。

3.2 姿态动力学方程ESO设计

根据式(28)的无人直升机姿态动力学方程设计扩张状态观测器,在线估计角速度、实际力矩以及总扰动,有

(30)

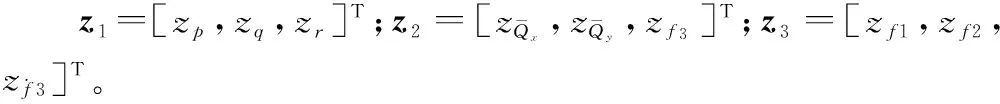
4 控制器设计

4.1 控制目标

本文的控制目标是:对任意给定的二阶可微的参考轨迹Pd,设计轨迹跟踪控制器,使得无人直升机系统式(27)和式(28)位置P在有外界干扰以及内部惯性参数摄动的情况下跟踪到期望轨迹上,且保证其他状态参数有界。无人直升机控制量分别为主旋翼总距θ0、尾桨总距θtr以及主旋翼纵向/横向周期变距θ1c和θ1s,其控制结构图如图1所示。

图1 无人直升机轨迹鲁棒控制结构图Fig.1 Block diagram of trajectory robust control for unmanned helicopter

4.2 位置控制器

定义位置误差和速度误差项

eP=P-Pd,eV=V-Vd

(31)

设计控制律

(32)

(33)

质量m自适应调整律

(34)

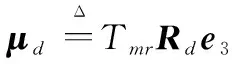
(35)

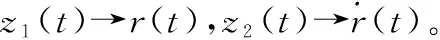
定理1通过式(32)～式(34),可使得位置子系统式(27)渐近收敛到零。

证明选择Lyapunov候选函数

(36)

对式(36)两边求导,且将式(27)代入

将控制律式(32)～式(34)代入可得

证毕

由于R∈SO(3),则‖Rde3‖=1。故根据式(33)可求得主旋翼升力和升力期望作用方向分别为

Tmr=‖μd‖

(37)

(38)

(39)

(40)

Rd2=Rd3×Rd1

(41)

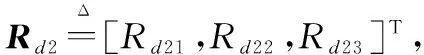
φd=arctan(Rd23/Rd33)

(42)

4.3 姿态控制器

定义姿态误差和角速度误差分别为

eΘ=Θ-Θd,eω=ω-ωd

(43)

设计控制律

(44)

(45)

及转动惯量ρ自适应调整律

(46)

定理2通过式(44)～式(46),可使得姿态子系统式(28)渐近收敛到零。

证明选择Lyapunov候选函数

(47)

对式(47)两边求导,并代入式(28),有

将式(44)～式(46)代入可得

证毕

4.4 力矩控制器

(48)

选择Lyapunov候选函数

(49)

对式(49)两边求导,并将式(25)代入,有

(50)

式中,Δf12,eso表示利用ESO对不确定项f12的观测值;eω12表示角速度误差向量eω的前两行。选取控制量

(51)

(52)

从而可得尾桨总距为

(53)

式中,Δf3,eso表示利用ESO对不确定项f3的观测值。

最后,利用式(12)、式(13)以及式(37)的主旋翼拉力Tmr即可求出主旋翼总距。至此,得到了无人直升机系统全部的控制量。

5 仿真与分析

为了模拟燃油消耗的作用,让无人直升机总重在整个仿真过程中均匀减少3 kg,即m(k)=m0-(3/n)·k,其中m0为飞机起飞重量,n为仿真总步数,k为当前仿真步数。同时,在t=10 s时将惯性矩阵J中各元素突变为Ixx=0.386 3,Iyy=0.480 6,Izz=0.474 1,直到仿真结束。在仿真过程中模拟了未建模动态及外界阵风的扰动作用,利用文献[20]类似的Gauss-Markov过程产生均值为零、幅值为3的高斯白噪声,如图2表示。

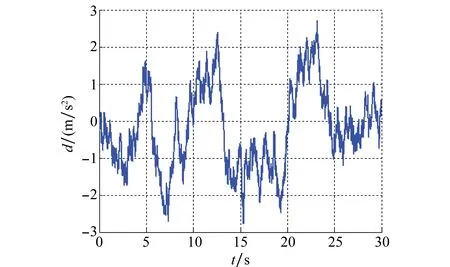
图2 模拟的作用在系统中的扰动Fig.2 Simulated disturbance acting on the system

无人直升机轨迹跟踪仿真结果如图3～图8所示,其中“ESO-ABC”为本文提出的基于ESO的自适应反步控制方法,“ABC”表示常规自适应反步控制方法。图3和图4分别为无人直升机三维和二维轨迹跟踪曲线,图5为位置跟踪误差。从图3～图5可以看到,本文所提出的方法比常规自适应反步法具有更好的轨迹跟踪效果,响应时间更快、鲁棒性更好,扰动抑制效率更高。

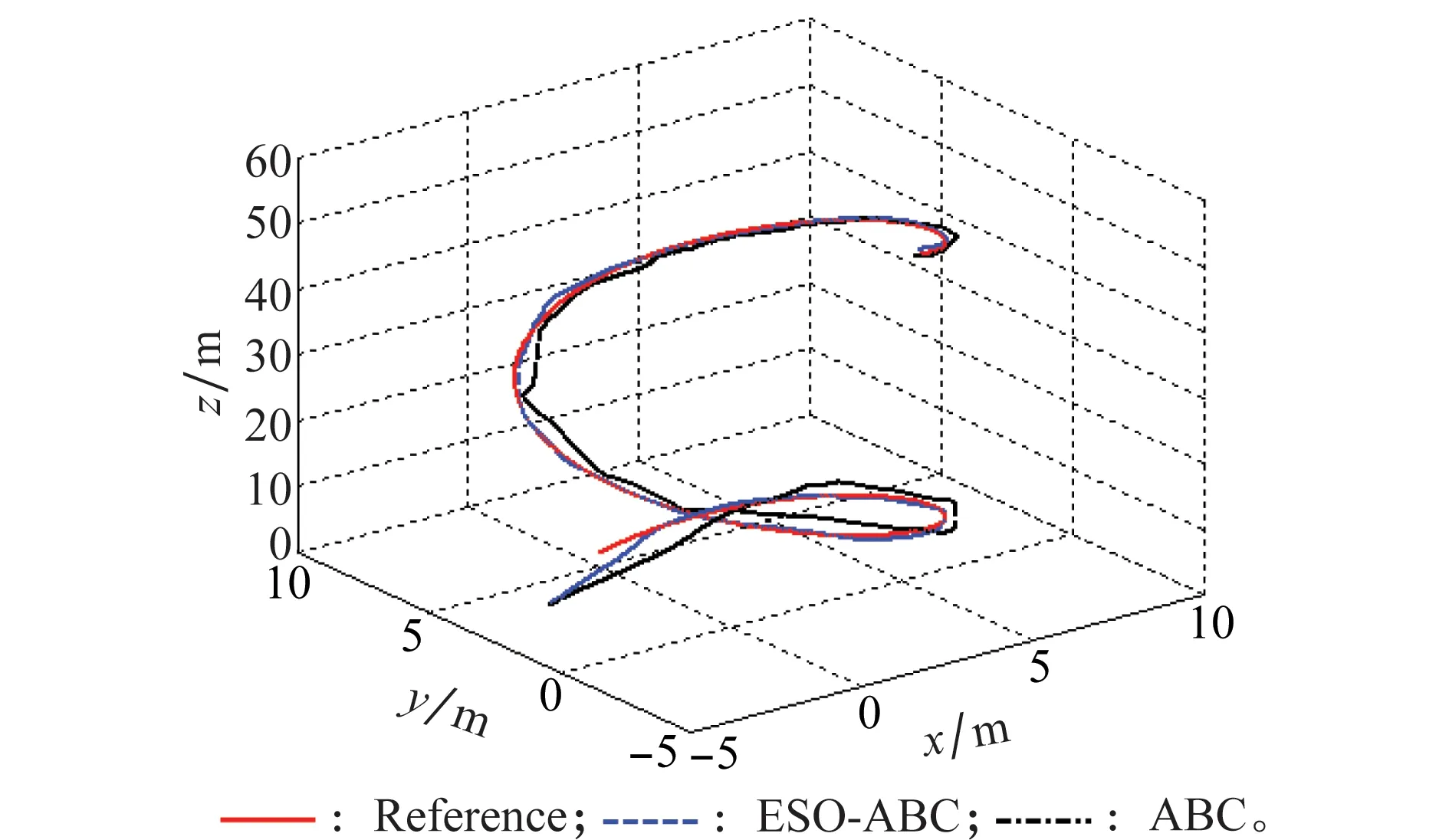
图3 三维轨迹跟踪结果Fig.3 Three dimensional trajectory tracking results

图4 位置轨迹曲线Fig.4 Position trajectory curves

图5 位置跟踪误差Fig.5 Position tracking errors

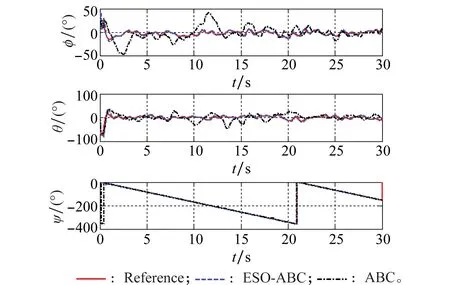
图6 姿态跟踪结果Fig.6 Attitude tracking results

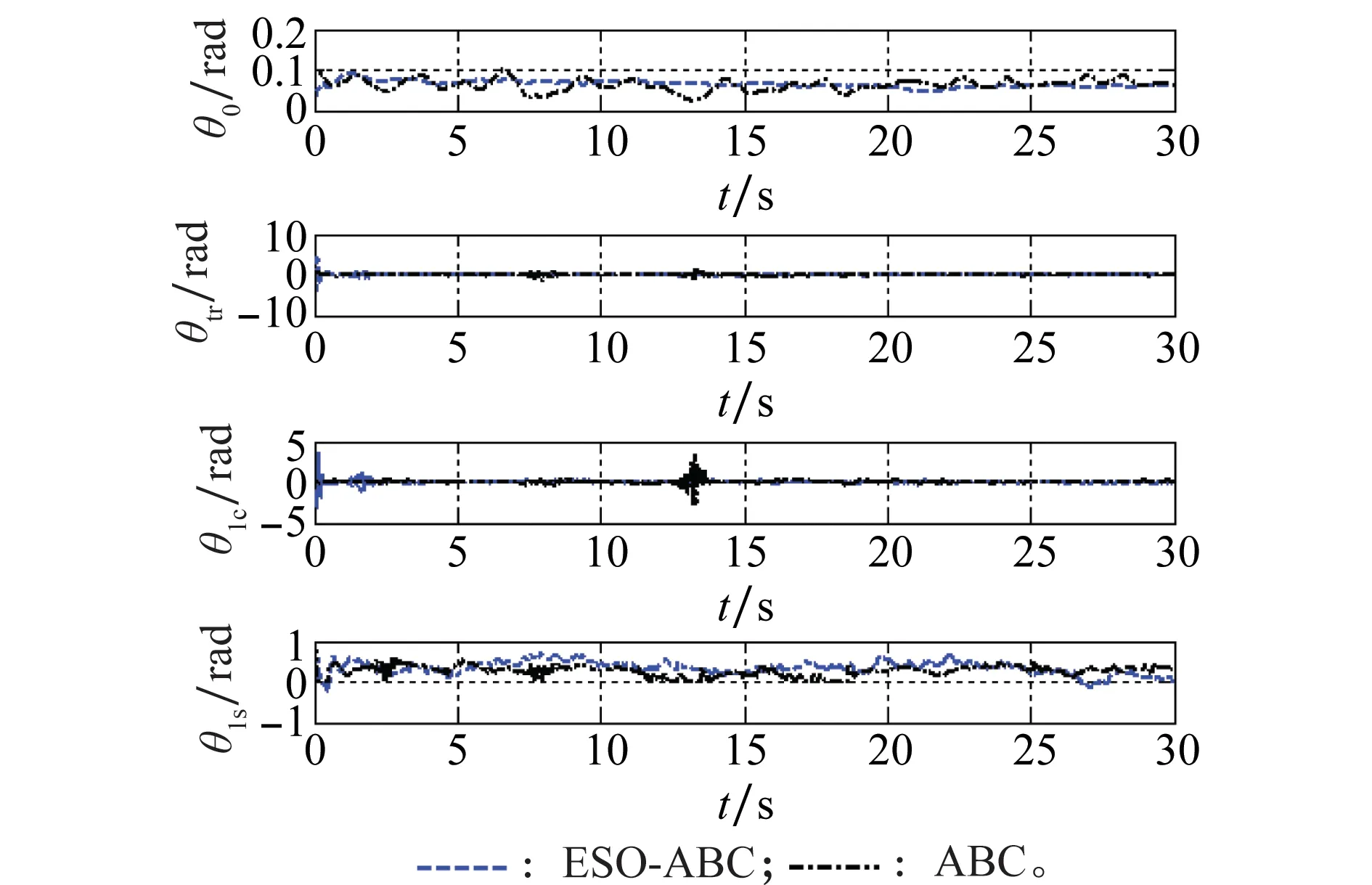
图7 控制输入信号Fig.7 Control input signal

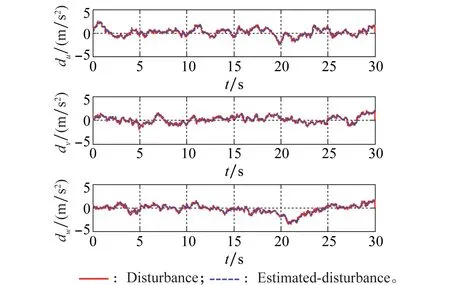
图8 扰动的ESO观测值Fig.8 Disturbances of the ESO

图6为姿态跟踪曲线。从图中可以看到,由本文所提方法得到的实际姿态与期望姿态曲线基本重合,而常规反步法在俯仰角和滚转角的跟踪上都存在较大振荡。图7为控制输入信号,表明在加入ESO后无人直升机输入控制信号仍在合理的范围内,未出现较大幅值和反复的控制量调节,在实际飞行中是可实现的。图8为对位置动力学方程中干扰信号d1=[du,dv,dw]T的ESO估计效果。显然,对于随机扰动的估计ESO能达到满意的效果。

6 结 论

针对无人直升机实际飞行控制中存在的未建模动态、模型简化误差以及由于燃油消耗导致的质量和惯性矩阵参数摄动等不确定性问题,提出了一种具有较强鲁棒性的非线性控制方法,即基于ESO的自适应反步鲁棒控制方法,通过数值仿真验证了该方法的有效性。仿真结果表明,在多种类型的不确定性并存的情况下,本文所提出的综合方法无论在跟踪精度、响应速度,还是扰动抑制效率等方面都比常规自适应反步法具有一定的优势,它能显著增强无人直升机在飞行过程中的抗干扰性以及对参数摄动的自适应性。

[1] GONG X, WANG L, MENG Z. Fuzzy self-tuning PID controller for an unmanned helicopter[C]∥Proc.of the IEEE Control Conference, 2015: 3635-3641.

[2] KADMIRY B, DRIANKOV D. A fuzzy gain-scheduler for the attitude control of an unmanned helicopter[J]. IEEE Trans.on Fuzzy Systems, 2012, 12(4):502-515.

[3] LIU P, MENG Z, WU Z. A robust flight control system design for a small-scale UAV helicopter[J]. Transactions of the Japan Society for Aeronautical & Space Sciences, 2013, 56(2):96-103.

[4] CHEN Y, WANG X, LU G, et al. Modeling and LQR control of small unmanned helicopter[C]∥Proc.of the IEEE Control Conference, 2013:4301-4305.

[5] KANG K, PRASAD J V R, JOHNSON E. Active control of a UAV helicopter with a slung load for precision airborne cargo delivery[J]. Unmanned Systems, 2016, 4(3):213-226.

[6] FANG X, WU A, SHANG Y, et al. A novel sliding mode controller for small-scale unmanned helicopters with mismatched distur-bance[J].Nonlinear Dynamics,2016,83(1/2):1053-1068.

[7] SAMAL M K, GARRATT M, POTA H, et al. Model predictive attitude control of vario unmanned helicopter[C]∥Proc.of the IEEE 37th Annual Conference on Industrial Electronics Society, 2011: 622-627.

[8] ABASPOUR A, SADATI S H, SADEGHI M. Nonlinear optimized adaptive trajectory control of helicopter[J]. Control Theory and Technology, 2015, 13(4):297-310.

[9] HE Y B, PEI H L, ZHOU H B. Command filtered backstepping-based flight control of unmanned helicopters with distur-bance observers[C]∥Proc.of the IEEE Control Conference, 2015:5581-5586.

[10] 高志强. 控制工程的抗扰范式[C]∥中国控制会议, 2010: 6071-6076.

GAO Z Q. On disturbance rejection paradigm in control engineering[C]∥Proc.of the IEEE Control Conference, 2010: 6071-6076.

[11] YAO Z. Adaptive trajectory tracking control approach for a model-scaled helicopter[J]. Nonlinear Dynamics, 2016, 83(4): 2171-2181.

[12] ZHU B, HUO W. Adaptive backstepping control for a miniature autonomous helicopter[C]∥Proc.of the 50th IEEE Conference on Decision and Control and European Control Conference, 2011: 5413-5418.

[13] ZUO Z Y, RU P K. Augmented L1 adaptive tracking control of quad-rotor unmanned aircrafts[J]. IEEE Trans.on Aerospace & Electronic Systems, 2014, 50(4):3090-3101.

[14] HE Y B, PEI H L, ZHOU H B, et al. Adaptive backstepping-based robust tracking control of unmanned helicopters with disturbances[J]. Control Theory & Applications, 2013, 30(30):834-843.

[15] 朱亮. 空天飞行器不确定非线性鲁棒自适应控制[D]. 南京:南京航空航天大学, 2006.

ZHU L. Robust adaptive control for uncertain nonlinear systems and its applications to aerospace vehicles[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2006.

[16] 韩京清. 自抗扰控制技术: 估计补偿不确定因素的控制技术[M]. 北京:国防工业出版社, 2008.

HAN J Q. Active disturbance rejection control technique: the technique for estimating and compensating the uncertainties[M]. Beijing: National Defense Industry Press,2008.

[17] RAPTIS I A, VALAVANIS K P. Linear and nonlinear control of small-scale unmanned helicopters[M]. Dordrecht: Springer, 2011.

[18] BRAMWELL A R S,DONE G,BALMFORD D.Bramwell’s helicopter dynamics[M].2nd ed. Woburn:Butterworth-Heinemann, 2000.

[19] CHEN R T N. Effects of primary rotor parameters on flapping dynamics, NASA technical paper 1431[R]. National Aeronautics and Space Administration Scientific and Technical Information Office, 1980.

[20] ZOU Y, HUO W. Adaptive tracking control for a model helicopter with disturbances[C]∥Proc.of the American Control Conference, 2015: 3824-3829.