基于典型散射差异指数的PolSAR图像Lee滤波

韩 萍, 韩宾宾

(中国民航大学天津市智能信号与图像处理重点实验室, 天津 300300)

0 引 言

极化合成孔径雷达(polarimetric synthetic aperture radar,PolSAR)是一种先进的雷达成像系统,它具有全天时、全天候、高分辨率的特点。由于系统固有缺陷,PolSAR图像存在严重的相干斑噪声,它不仅降低了图像的视觉效果,而且也降低了后续分类、目标检测和识别等处理的精度[1-3]。因此,PolSAR图像相干斑抑制研究是图像解译预处理的主要内容之一[4-6]。

由于通道串扰,PolSAR图像的相干斑抑制更加复杂。早期具有代表性的滤波算法有极化白化滤波[7]、最优加权滤波[8]和极化矢量滤波[9],这些算法的主要问题是引入了通道串扰,目标的极化特性没有得到很好保持;文献[10] 提出PolSAR图像的相干斑滤波准则,该准则指出,为避免通道串扰和保持目标的极化特征,应尽可能地选取与滤波像素相近的邻域像素进行同等程度的滤波。基于该准则,文献[10] 同时给出基于边缘配准窗和最小均方误差滤波器的精致Lee滤波算法,目前很多滤波算法都在该算法的基础上发展而来[11-17],如基于散射模型的PolSAR滤波算法、基于多级分类的滤波算法以及自适应增强Lee滤波算法等。这些算法主要对滤波像素筛选方法进行了改进,可以分为3类:①基于模板窗的邻域像素筛选,这类算法的优点是筛选速度快,缺点是模板筛选隐含假设模板内部像素为同质像素,这种假设在纹理丰富区域可能不成立;②基于分类的邻域像素筛选,这类算法利用未滤波数据进行分类,然后以分类结果为依据进行同质像素筛选,缺点是分类结果可靠性比较低;③基于相似性度量的邻域像素筛选,这类算法通过对邻域像素与滤波像素的相似性进行度量,选择相似度比较大的邻域像素作为同质像素,能否综合利用PolSAR图像的极化信息来度量像素相似性是这类算法的关键。

基于分析,本文提出基于典型散射差异指数(typical scattering difference index, TSDI)的PolSAR图像Lee滤波算法。该算法首先引入TSDI度量,TSDI能够综合利用PolSAR图像3个极化通道数据度量滤波像素与邻域像素的相似程度,然后基于该度量采用自适应阈值法筛选出滤波像素的同质像素,之后再用筛选的同质像素进行Lee滤波。对于筛选阈值,首先利用Parzen窗估计同质区域TSDI的概率分布,然后根据估计结果计算阈值。因为算法的同质像素筛选过程综合利用了PolSAR数据极化特性,因而同质像素与滤波像素更加相近,滤波结果相对于精致Lee滤波结果相干斑抑制更加彻底,同时图像边缘清晰度和目标极化特性保持更加完好。

1 极化相干矩阵

对于单站雷达,在满足互易性假设下,极化散射信息可以表示成如下复数矩阵形式

(1)

式中,SXX和SYY分别为X通道和Y通道发射接收极化散射系数；SXY为X通道发射Y通道接收极化散射系数。所谓互易性,即X通道发射Y通道接收回波系数等于Y通道发射X通道接收回波系数。为抑制相干斑,PolSAR数据通常会进行多视处理:

(2)

式中,T为常用的PolSAR图像相干矩阵；Tij为相干矩阵T元素；L表示PolSAR图像的视数。

文献[18-19]提出散射相似性参数的概念,利用PolSAR目标的相干矩阵与典型散射体的Pauli矢量计算而得

(3)

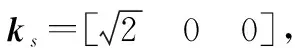
结合式(3),容易得到任意相干矩阵与3种典型散射体的相似性参数

(4)

式中,rs为奇次散射相似性参数;rd为偶次散射相似性参数;rv为体散射相似性参数;y为目标散射功率。由式(4)可以看出,T11可以解释为目标的奇次散射能量;T22为偶次散射能量;T33为体散射能量。

2 精致Lee滤波

精致Lee滤波主要包括以下两个步骤:

步骤1利用模板筛选同质像素:Lee设计的8个边缘模板如图1所示。按文献[10] 步骤,利用功率图计算边缘方向,并将模板内部白色像素作为同质像素参与到模板中心像素滤波中。

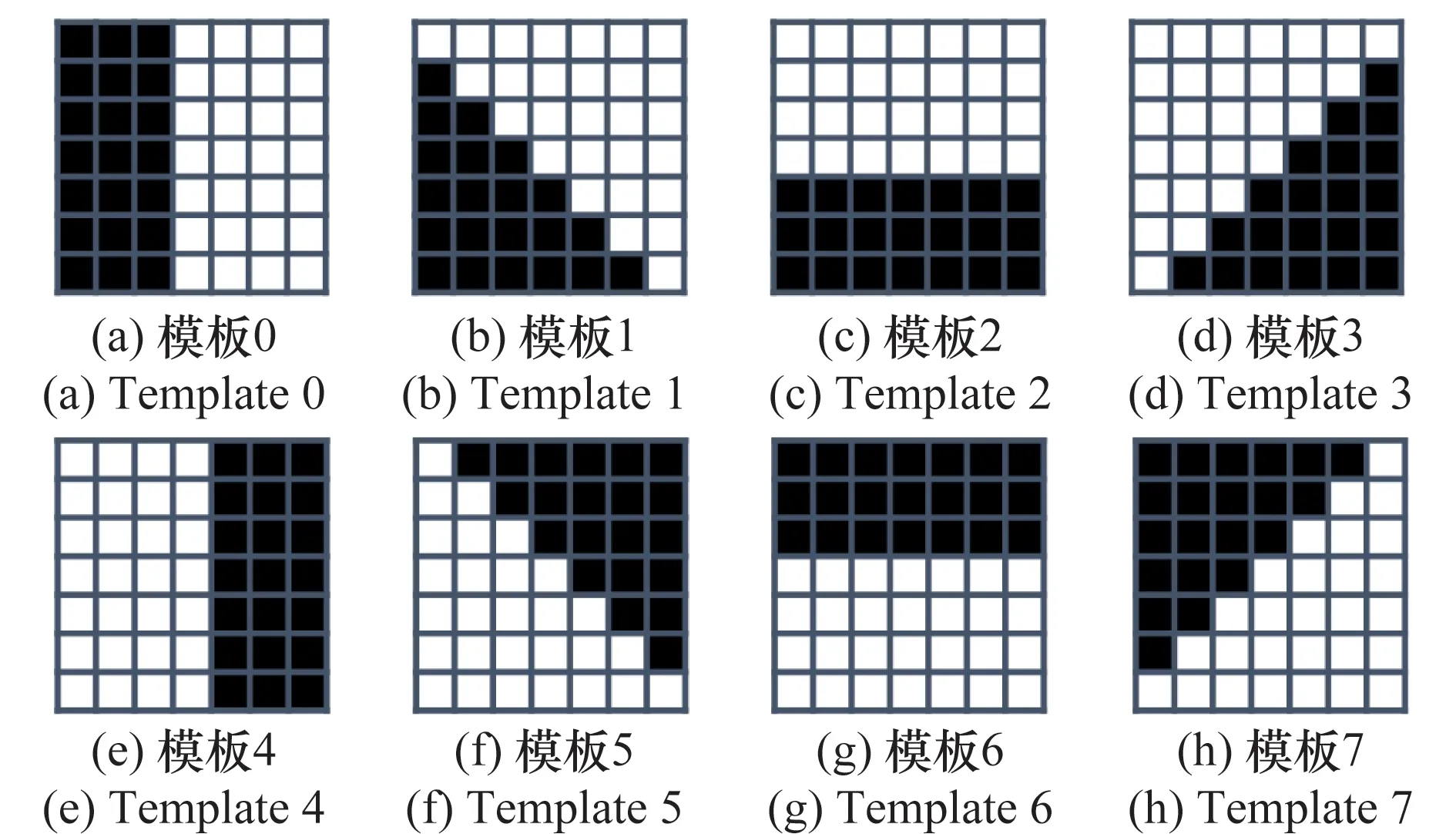
图1 精致Lee滤波的8种边缘模板Fig.1 8 edge-directed template of Refine-Lee filter

(5)

3 本文方法

算法首先引入TSDI,该指数能够全面地利用PolSAR数据极化信息进行像素筛选,因而筛选的邻域像素比精致Lee滤波更加相近中心像素,滤波后图像边缘和目标极化信息保持更加完好。本文所提算法的基本思路为:①利用滤波像素与邻域像素之间的TSDI,采用自适应阈值法选出滤波像素的同质邻域像素;②利用同质邻域像素进行Lee滤波。算法流程图如图2所示。

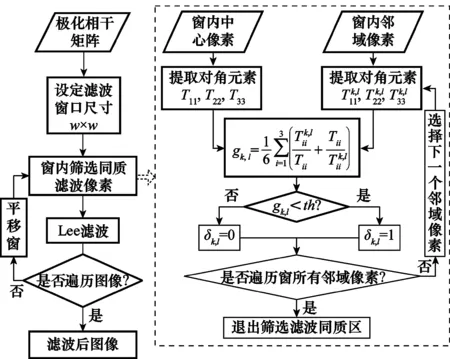
图2 算法流程图Fig.2 Flow chart of algorithm

3.1 典型散射差异指数TSDI

在局部区域内,如果两个像素的奇次散射能量、偶次散射能量和体散射能量都相近,则可以认为这两个像素属于相同的散射体。基于该原则,引入TSDI概念:

(6)

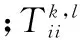
(1)g≥1,当且仅当两个目标的3种散射能量都相等时,典型散射差异指数g=1;

(2) 两目标相干矩阵的差异性越大,典型散射差异指数g值越大;

(3) 典型散射差异指数g只与两目标相干矩阵对角元素的相对差异有关。

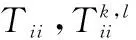
3.2 基于Parzen窗的TSDI分布估计

为确定同质像素筛选的判决阈值,对同质区域的TSDI概率分布进行统计,并用Parzen窗概率密度估计方法[20-21]拟合概率分布。Parzen窗概率密度估计方法在很多领域都有广泛应用,它以数据样本为中心利用窗函数对概率密度函数进行插值拟合。当数据样本足够大时,该方法能够给出相当准确的概率密度估计。

假设样本集合X={x1,x2,…,xM},Parzen窗概率密度函数为

(7)

式中,ke(·)表示Parzen窗的核函数,可以是矩形函数、高斯函数等；h表示核函数的宽度；M表示样本个数。本文使用最常用的Gauss窗函数和文献[22] 给出的最优窗宽度,即

(8)

式中,σ表示样本标准差。

考虑到TSDI取值范围比较大,为减少估计误差,先对TSDI取自然对数再用Parzen窗进行估计

x=ln(g)

(9)

得到同质区域TSDI的概率密度p(x)后,由给定检测率Pd可确定对应的筛选阈值th：

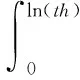
(10)

利用筛选阈值,在中心像素邻域内进行如下方式的同质像素筛选：

(11)

式中,δk,l=1表示窗内(k,l)位置像素为当前滤波像素的同质像素,参与Lee滤波;相反,δk,l=0表示(k,l)位置像素为非同质像素,不参与滤波。

4 实验及分析

为了验证本文算法的有效性,分别利用美国AIRSAR系统和UAVSAR系统采集的多幅图像进行实验,由于篇幅所限本文只给出San Francisco地区和Gulf Coast地区的部分实验结果。AIRSAR系统采集的San Francisco地区PolSAR数据如图3(a)所示,数据大小为900×700,数据包含了海洋、森林、城区等典型地物。UAVSAR系统采集的Gulf Coast地区PolSAR数据如图3(b)所示,数据大小为401×675,数据场景为局部机场区域,既有匀质的道路、水体和植被,又有纹理丰富的城区,还有一些明显的点、线目标。

图3 实验数据PauliRGB图Fig.3 PauliRGB image of experiment data

图3(a)中圆角矩形区域是海洋,以表面散射为主,总像素为22 000,图3(b)圆角矩形区域是植被,以体散射为主,总像素数为21 343。这些区域的散射特性分布比较均匀,适合用来估计TSDI的概率分布。由于数据样本比较大,可以把平均相干矩阵作为目标真实相干矩阵。区域内相干矩阵与平均相干矩阵的自然对数TSDI概率分布和Parzen窗估计结果如图4所示。火柴杆图为真实TSDI概率分布,实曲线为拟合结果,由图4可知,Parzen窗较好地拟合了TSDI概率分布。χ2检验是一种通用的假设检验方法,如果χ2匹配系数小于卡方临界值,则接受估计结果作为真实结果。San Francisco地区和Gulf Coast地区的χ2匹配系数分别为210.9和229.9,χ2临界值为254.13,可以接受两种估计分布为真实概率分布。比较图4(a)和图4(b)可知,虽然San Francisco和Gulf Coast的采集系统不同,目标散射类型也不同,但TSDI概率分布仍一致,说明TSDI具有较高的鲁棒性。[0.5,1.0]范围内的TSDI和对应检测概率如表1所示。由表1可知，当ln(th)>0.5即th>1.65时两个地区都能达到90%以上的检测概率;当ln(th)>1.0即th>2.72时能达到98%以上,在[1.65,2.72]之间随机选取阈值也能取得不错的筛选结果。针对不同PolSAR图像可以采用两种阈值选取方式:①当PolSAR图像存在大片匀质区域时可以用Parzen窗估计TSDI概率分布,再由检测概率确定筛选阈值;②当PolSAR图像不存在大片匀质区域时,可在[1.65,2.72]随机选取阈值。

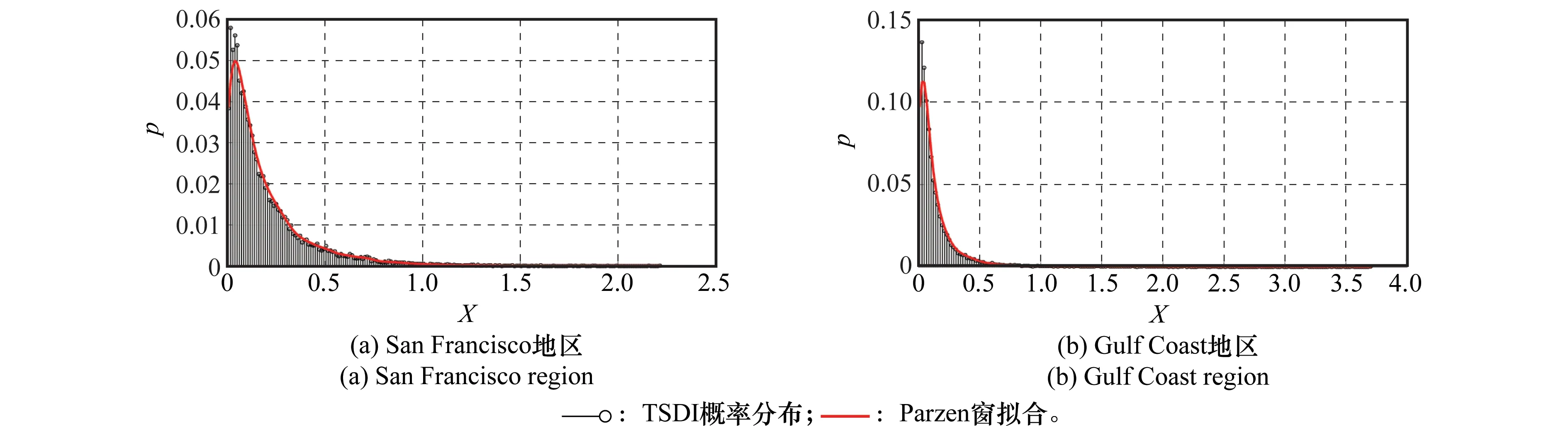
图4 均匀区域典型散射差异指数分布与拟合Fig.4 Distribution and fitting result of typical scattering difference index in homogeneous region

对数典型散射差异指数ln(g)0.50.60.70.80.91.0典型散射差异指数g1.651.822.012.232.462.72SanFrancisco检验概率Pd0.920.940.970.980.990.99GulfCoast检验概率Pd0.950.960.970.980.980.99

4.1 视觉效果评价

为验证改进算法的有效性,首先从视觉角度对滤波结果进行比较。PauliRGB图除了能够表示目标的强度信息,也能表示目标的散射信息和极化信息,在PauliRGB图中进行视觉分析能更全面地表现各种算法的滤波效果。

San Francisco地区的滤波结果如图5所示,其中图5(a)为原始PauliRGB图,本文对图中一些典型的散射目标进行了标注,1区为山林,2区为海洋,3区为城区,4区为金门大桥,5区为高尔夫球场,6区为跑马场,7区为城区主干道。实验分别选取了5×5,7×7,9×9,11×11这4种窗,对精致Lee滤波和本文算法进行比较。由于文献[10] 只给出7×7窗的滤波结果,为便于比较本文也只给出窗口为7×7的滤波结果。图5(b)为精致Lee滤波后的PauliRGB图;图5(c)为本文方法滤波后的PauliRGB图。从图中可以看出,两种滤波算法都较好地抑制了相干斑,海洋和跑马场区域的视觉效果有所改善;但是,精致Lee滤波算法在纹理信息丰富的区域产生了过度平滑,比如高尔夫球场的纹理模糊严重,城区的块状效应非常明显,且城区的道路出现了断断续续的情况,甚至一些小的道路消失不见。而本文算法则在这方面表现较好,图中城区、高尔夫球场的纹理和城区道路都清晰可见。Gulf Coast地区的滤波结果如图6所示。从整体上看,本文算法的视觉效果更加自然,同质区域非常平整,点、线目标清晰,城区的清晰度明显改善。

4.2 定量评价

采用常用的PolSAR图像滤波评价指标等效视数(equivalent number of looks,ENL)和边缘保持指数(edge preserved index,EPI)进行定量分析。ENL越大表明图像相干斑越小,算法抑制效果越好;EPI越接近1,表明算法目标保持效果越好。图7给出了计算各项指标的采样区域;表2和表3分别给出了San Francisco和Gulf Coast地区的计算结果。

图5 San Francisco地区滤波效果Fig.5 Filter effect in San Francisco region

图6 Gulf Coast地区滤波效果Fig.6 Filter effect in Gulf Coast region

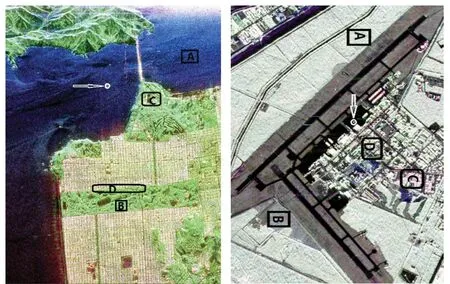
图7 ENL和EPI分析的数据采样区域Fig.7 Sampling regions for ENL and EPI analysis

图7中选择A区、B区计算ENL,其中San Francisco地区的A区和B区分别为海洋和森林,Gulf Coast地区的A区和B区分别为灌木林和草坪,这些区域的散射特性比较均匀单一,可以看成同质区域;选择C区、D区计算EPI,San Francisco地区的C区和D区为山顶建筑物和城区边界,Gulf Coast地区的C区和D区为机场周边建筑,这些区域边缘丰富。如表2和表3所示,滤波前A区和B区的ENL都比较低,相干斑严重;滤波后两个区域的ENL都有所增加,而且两种方法都符合一个比较普遍的认知:窗口越大,相干斑抑制越好,ENL越大。对比来看,本文方法的ENL要高于精致Lee滤波算法,这说明新方法的相干斑抑制能力更强。相对应的,滤波后两种滤波算法都损失了一定的边缘信息,从表1看出,San Francisco地区的EPI,除9×9窗外新方法都高于精致Lee滤波;Gulf Coast地区的EPI,新方法在各种窗口下都高于精致Lee滤波,这说明新方法的图像边缘保持能力更好。而且,随着窗口增大本文方法的ENL和EPI都有增大的趋势,这是因为窗口越大同质区筛选可选的邻域像素越多。但是,随着窗口增大本文算法的运算量也迅速增大,如以w×w窗对大小m×n的PolSAR图像进行滤波,同质区筛选需要进行6mnw2次除法运算和5mnw2次加法运算,运算量与窗口尺寸的平方成正比。因此，本文算法适合应用在对图像实时处理要求不高的场合。综合考虑滤波效果和运算量,9×9和11×11是比较理想的滤波窗口。

表2 San Francisco地区的ENL和EPI定量分析表

表3 Gulf Coast地区的ENL和EPI定量分析表

4.3 极化特性保持评价

为比较两种算法的极化特性保持能力,图8和图9给出了7×7窗口的点目标同极化响应和交叉极化响应图。采样点的位置如图7箭头所示,San Francisco地区的采样点为海洋中的舰船,坐标为(260,332);Gulf Coast地区的采样点为停机坪上的飞机,坐标为(170,282),它们都与周围目标存在较大的散射差异。从图8和图9中容易看出本文算法的极化保持能力要好于精致Lee滤波。进一步的分析表明,这是因为精致Lee滤波筛选出的邻域像素与中心像素存在较大差异所致,而本文方法筛选的邻域像素与中心像素差异较小。图10给出了San Francisco地区采样点的滤波像素筛选情况,白色表示参与滤波的像素。精致Lee算法选择中心点下方所有像素参与滤波,这些像素中混杂了很多海洋目标,而本文算法只选用与中心像素比较相近的10个像素参与滤波。

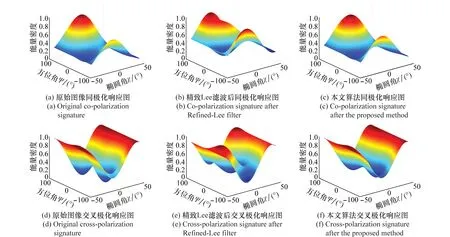
图8 San Francisco地区图中(260,332)的目标同极化和交叉极化响应图Fig.8 Co-polarization and cross-polarization signatures of(260,332) pixel in San Francisco region

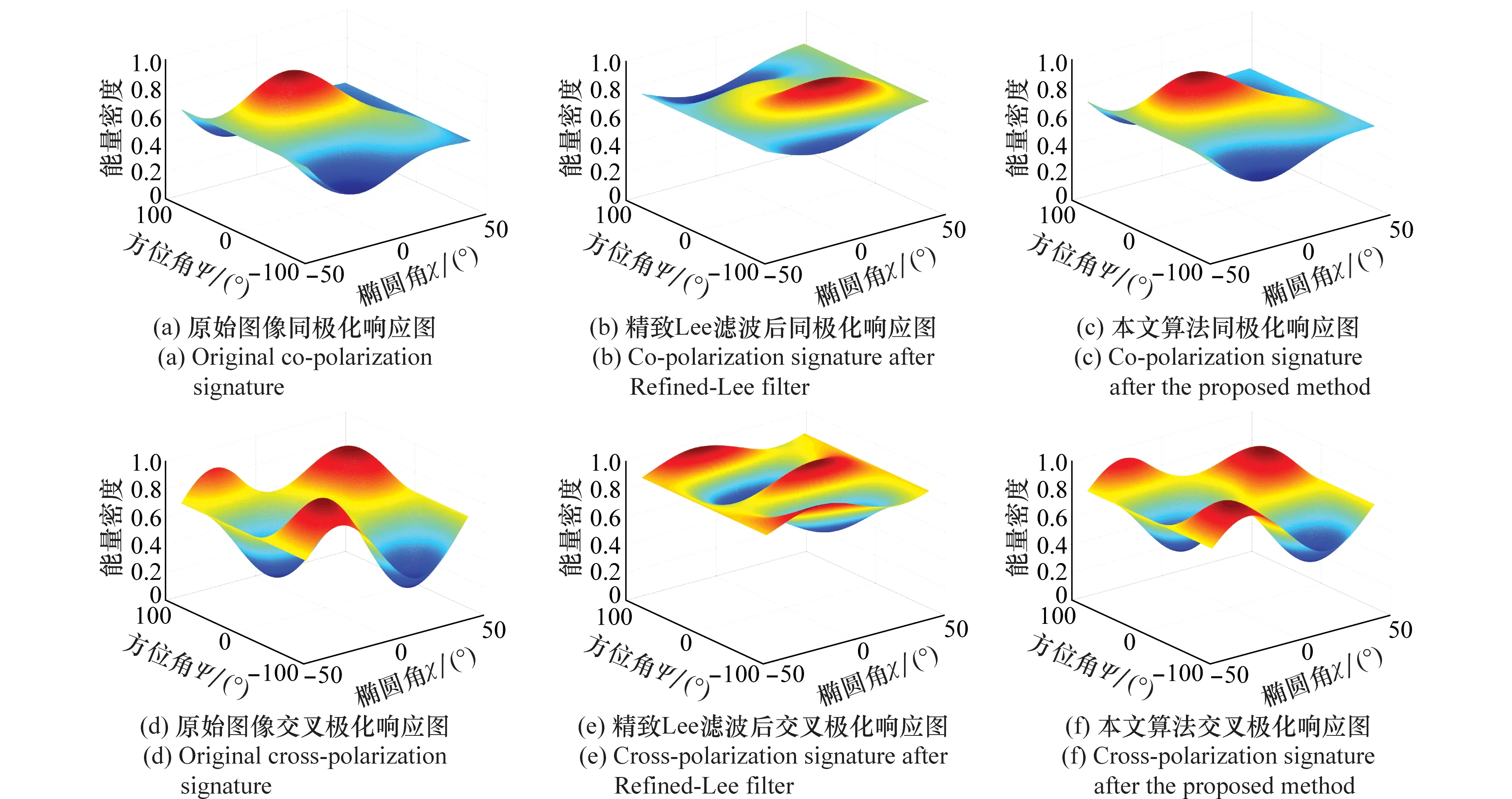
图9 Gulf Coast地区图中(170,282)的目标同极化和交叉极化响应图Fig.9 Co-polarization and cross-polarization signatures of (170,282)pixel in Gulf Coast region

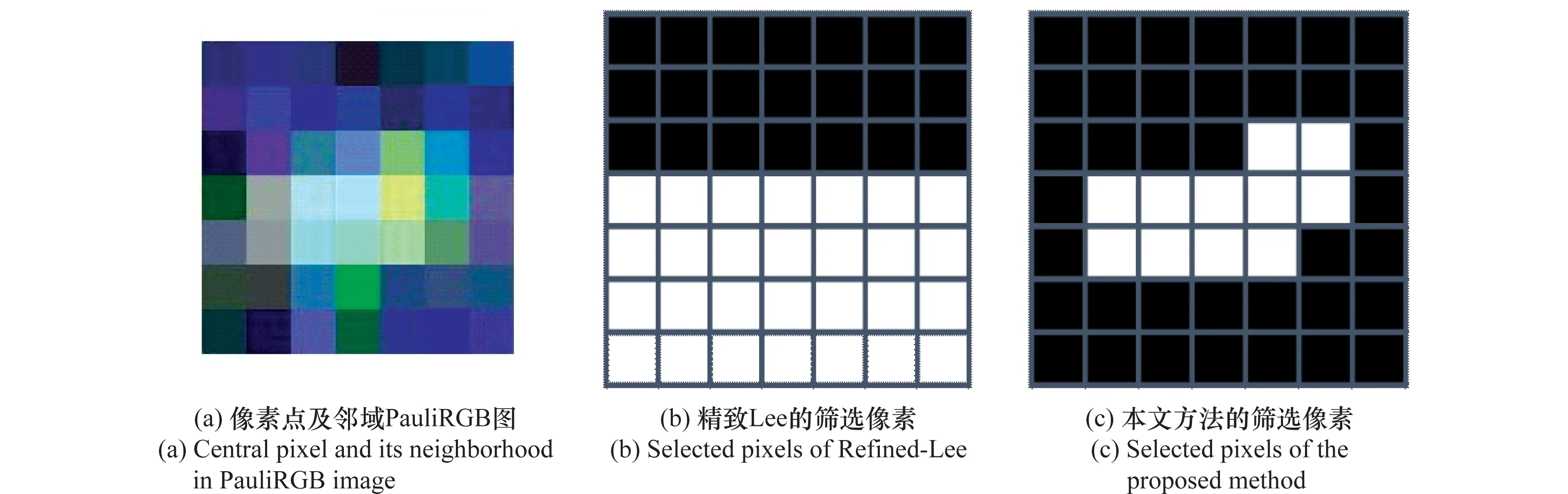
图10 San Francisco地区极化特性分析采样点筛选的邻域滤波像素Fig.10 Selected neighborhood pixels of sampling point for polarimetric characteristic analysis in San Francisco

5 结 论

针对滤波后PolSAR图像的边缘和目标的极化特性保持不够理想的问题,本文提出基于TSDI的PolSAR图像Lee滤波算法。算法利用滤波像素和邻域像素之间的TSDI,采用自适应阈值法选出滤波像素的同质像素进行Lee滤波。利用实测数据进行实验,结果表明本文滤波效果优于精致Lee滤波。算法在滤波过程中需要逐个对图像像素进行同质像素筛选,其运算量与邻域窗口平方成正比,运算量相对于精致Lee滤波较大,如何减少运算量是下一步要研究的重点。

[1] GU J, YANG J, ZHANG H, et al. Speckle filtering in polarimetric SAR data based on the subspace decomposition[J]. IEEE Trans.on Geoscience & Remote Sensing, 2004, 42(8): 1635-1641.

[2] KERSTEN P R, LEE J S, AINSWORTH T L. Unsupervised classification of polarimetric synthetic aperture radar images using fuzzy clustering and EM clustering[J]. IEEE Trans.on Geoscience & Remote Sensing, 2005, 43(3): 519-527.

[3] VASILE G, TROUVE E, LEE J S, et al. Intensity-driven adaptive neighborhood technique for polarimetric and interferometric SAR parameters estimation[J]. IEEE Trans.on Geoscience & Remote Sensing, 2006, 44(6): 1609-1621.

[4] 周晓光, 匡纲要, 万建伟. 多极化SAR图像斑点抑制综述[J]. 中国图象图形学报, 2008, 13(3): 377-385.

ZHOU X G, KUANG G Y, WAN J W. A review of polarimetric SAR speckle reduction[J]. Journal of Image & Graphics, 2008, 13(3): 377-385.

[6] LEE J S, AINSWORTH T L, WANG Y. On polarimetric SAR speckle filtering[C]∥Proc.of the IEEE Geoscience and Remote Sensing Symposium, 2012: 111-114.

[7] NOVAK L M, BURL M C. Optimal speckle reduction in polarimetric SAR imagery[J]. IEEE Trans.on Aerospace & Electronic Systems, 1990, 26(2): 293-305.

[8] LEE J, HOPPEL K, MANGO S A. Unsupervised estimation of speckle noise in radar images[J]. International Journal of Imaging Systems & Technology, 2010, 4(4): 298-305.

[9] LIN Q, ALLEBACH J P. Combating speckle in SAR images: vector filtering and sequential classification based on a multiplicative noise model[J]. IEEE Trans.on Geoscience & Remote Sensing, 1990, 28(28): 647- 653.

[10] LEE J S, GRUNES M R, GRANDI G D. Polarimetric SAR speckle filtering and its impact on classification[C]∥Proc.of the Geoscience and Remote Sensing, 1997: 1038-1040.

[11] LEE J S, GRUNES M R, SCHULER D L, et al. Scattering-model-based speckle filtering of polarimetric SAR data[J]. IEEE Trans.on Geoscience & Remote Sensing, 2006, 44(1): 176-187.

[12] 韩萍,董菲,吴仁彪.基于多级分类的极化SAR图像斑点抑制[J]. 系统工程与电子技术,2012,34(7): 1360-1365.

HAN P, DONG F, WU R B. PolSAR image speckle reduction based on multi-stage classification[J]. Systems Engineering and Electronics, 2012, 34(7): 1360-1365.

[13] LANG F, YANG J, LI D. Adaptive-window polarimetric SAR image speckle filtering based on a homogeneity measurement[J]. IEEE Trans.on Geoscience & Remote Sensing, 2015, 53(10): 5435-5446.

[14] LEE J S, AINSWORTH T L, WANG Y, et al. Polarimetric SAR speckle filtering and the extended sigma filter[J].IEEE Trans.on Geoscience & Remote Sensing,2015,53(3):1150-1160.

[15] 李平湘, 马晓双, 沈焕锋. 基于局部同质区最大化搜索的极化SAR影像最小均方误差滤波方法[J]. 测绘地理信息, 2016, 41(3): 1-7.

LI P X, MA X S, SHEN H F. A minimum-mean-square error filter based on the search of the maximal local homogenous area for PolSAR image despeckling[J]. Journal of Geomatics, 2016, 41(3): 1-7.

[16] 杨学志,陈靖,周芳,等.基于同质像素预选择的极化SAR图像非局部均值滤波[J].电子与信息学报,2015,37(12):2991-2999.

YANG X Z, CHEN J, ZHOU F, et al. Polarimetric SAR image despeckling using non local means filter based on homogeneous pixels preselection[J]. Journal of Electronics & Information Technology, 2015, 37(12): 2991-2999.

[17] 郎丰铠, 杨杰, 李德仁. 极化SAR图像自适应增强Lee滤波算法[J]. 测绘学报, 2014, 43(7): 690-697.

LANG F K, YANG J, LI D R. An adaptive enhanced Lee speckle filter for polarimetric SAR image[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 690-697.

[18] YANG J, PENG Y N, LIN S M. Similarity between two scattering matrices[J].Electronics Letters, 2001,37(3):193-194.

[19] AN W, ZHANG W, YANG J, et al. Similarity between two targets and its application to polarimetric target detection for sea area[C]∥Proc.of the 24th Progress in Electromagnetics Research Symposium, 2008:515-520.

[20] 张宏稷,杨健,李延,等.基于条件熵和Parzen窗的极化SAR舰船检测[J].清华大学学报,2012(12):1693-1697.

ZHANG H J, YANG J, LI Y, et al. Ship detection in polarimetric SAR images based on the conditional entropy and Parzen windows[J]. Journal of Tsinghua University, 2012(12): 1693-1697.

[21] DUDA R O, HART P E, STORK D G. Pattern classification[M].2nd ed. New York:Wiley, 2001.

[22] WASSERMAN L. All of nonparametric statistics (springer texts in statistics)[M]. New York: Springer-Verlag, 2006.