多源信息融合的组合导航自适应联邦滤波算法

段 睿, 张小红,2, 朱 锋

(1. 武汉大学测绘学院, 湖北 武汉 430079;2. 地球空间信息技术协同创新中心, 湖北 武汉 430079)

0 引 言

捷联惯导(strapdown inertial navigation system, SINS)具有完全独立自主、不受外界干扰、全天候工作的优点,能够连续输出稳定、低噪音的导航信息;在全球卫星导航系统(global navigation satellite system, GNSS)以及其他传感器的辅助下,以SINS为核心构建高精度定位、测速、测姿一体化的组合导航系统,是实现地理信息数据自动化采集的关键[1-2]。

在地面开阔的环境下,集成GNSS/SINS的定位定姿系统(position and orientation system,POS)可以提供高精度、稳定的外方位元素参考。然而,在地面复杂环境下,比如城市峡谷、隧道、高架桥等,由于信号遮挡及严重的多径问题,GNSS经常失锁,从而使导航系统误差快速积累。在这种情况下,集成基于多传感器的多源信息并实现优化融合成为首选方案。里程计(odometer,OD)[3]、零速修正(zero velocity update, ZUPT)[4]、非完整性约束(non-holonomic constraints, NHC)[5-6]等多源信息由于获取方便、成本低等优势,被广泛用作POS系统的外部更新信息源。

但由于这些信息的采集手段的限制,其观测结果往往容易产生粗差甚至出现错误,其动态模型也容易出现偏差,此时设计容错性能好,能有效抵御故障信息的融合器显得尤为重要。自从Carlson提出联邦滤波结构的分散化滤波器以来,由于其具有设计灵活,计算量小等优点而受到重视[7];另一方面,由于结构上各子系统相互隔离,易于实现系统错误的检测与排除[8],大批学者对基于联邦滤波器的多源信息融合方法进行了研究。房建成等设计了一种基于自适应模糊系统的联邦滤波智能容错结构方案,实现了SINS/GNSS/天文导航系统(celestial navigation system,CNS)组合系统的容错融合[9]。文献[10]在GNSS/INS/OD组合系统中利用模糊自适应卡尔曼滤波和加权的方法解决了传统联邦卡尔曼滤波器由于统计模型的不准确造成精度下降的问题,对结果有显著改善,同时提高了系统的稳定性。文献[11]结合联邦滤波和无迹滤波设计了无反馈的联邦滤波器,实现了SINS/GNSS/CNS的优化融合。利用联邦滤波进行融合的关键是其中信息分配系数的确定,它决定了滤波器的结构和性能。文献[12]提出了利用不同传感器局部估计的滤波方差进行自适应确定分配系数的方法。文献[13]利用Kalman滤波中新息易受观测误差和系统误差影响的特点,采用新息的协方差矩阵构造自适应分配系数。随后,联邦粒子滤波以及基于遗传算法的自适应信息分配方法也被用于多源信息融合[14-15]。

本文则从各子系统的验前新息出发,采用新息单位权中误差来计算联邦滤波器的分配系数,从而构建一种新的自适应联邦滤波算法,通过动态调节联邦滤波中的信息分配系数,对观测粗差和模型偏差引起的误差予以削弱,实现多源信息的优化融合。

1 多源信息融合的数学模型

在多源信息松组合导航系统中,以SINS为参考系统,GNSS等其他系统提供观测更新。以e系作为导航坐标系,则SINS的误差模型为

(1)

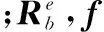
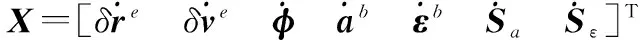
GNSS可以提供位置和速度信息,从而对SINS进行观测更新。里程计通过量测载体的前向速度来提供更新信息。零速修正基于载体静止时在e系下的速度为零这一原理,提供三轴速度信息进行更新。在地面车载导航中,不发生侧滑和跳动时,载体的侧向速度和垂向速度可认为为零,这样就可以利用此二维速度信息对载体运动进行约束,从而对系统进行更新,这种更新一般称作非完整性约束。其中,非完整性约束和里程计由于观测值的互补性,可以组成三轴速度观测信息进行更新[17]。

在本文中, GNSS,OD、零速修正、非完整性约束等多源信息将以松组合的形式参与融合,图1给出了多源信息融合的结构图。

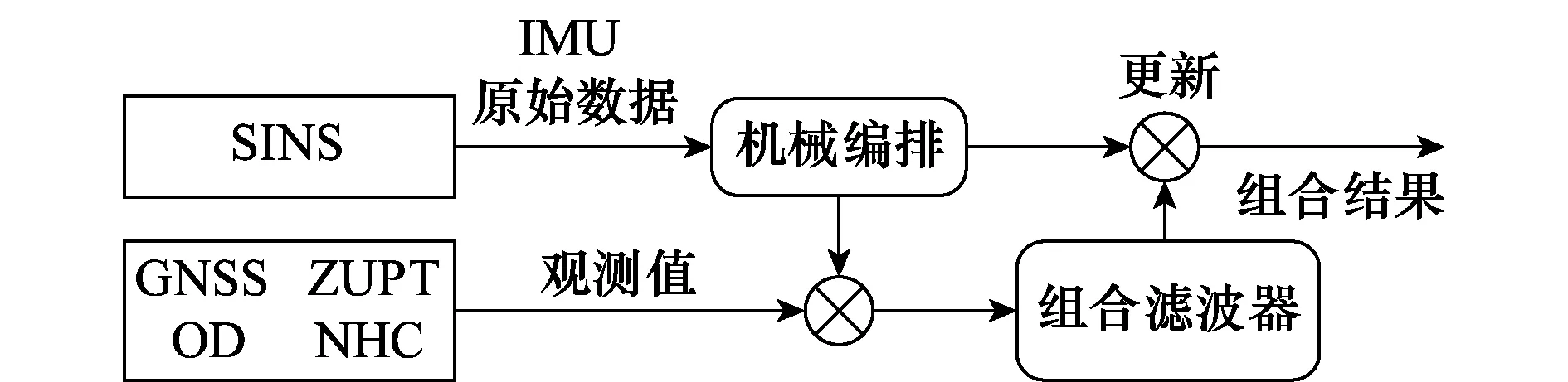
图1 多源信息松组合结构图Fig.1 Loosely-coupled structure of multi-sources information

2 联邦Kalman滤波

在多源信息融合导航系统中,联邦滤波器因为其计算量小、精度高、容错性能好而被广泛用于容错估计器的设计。由于各观测信息源相互独立,多源信息融合的联邦滤波器可表示为

(2)

联邦滤波器通过信息分配系数βi对滤波器进行调节[7]:

(3)

式中,Q为过程噪声方差。根据信息守恒原则,βi须满足∑βi=1。

每次滤波前,依据式(3)对滤波参数进行分配,进入各子滤波器进行滤波,然后进入主滤波器按式(2)进行融合。

图2给出了在多源信息融合中利用联邦滤波器进行融合的系统结构图。可以看到,各子滤波器的结果经过主滤波器融合之后得到当前历元的全局最优状态和方差,然后利用信息分配系数βi对全局状态和方差进行分配后又反馈给各子滤波器,从而进行下一次滤波。

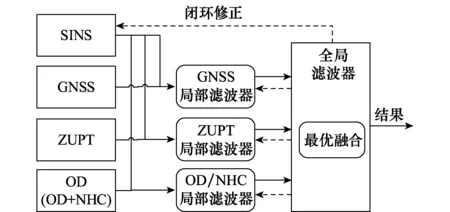
图2 多源信息融合联邦滤波结构Fig.2 Structure of federated Kalman filter in multi-sensor fusion system

3 自适应分配系数的确定

前面提到,联邦滤波器通过分配系数βi对滤波器进行控制和调整,其值的确定直接决定了滤波器的结构和性能。

一般而言,分配系数依据观测值的先验信息在滤波前给予固定的值。而在多源信息松组合导航系统中,各观测信息的观测质量并非固定不变。在开阔环境下,GNSS观测值质量较好,而在地面复杂环境下由于信号的遮挡和中断,其观测质量很差;里程计和非完整性约束在载体保持直线行驶时,其数学模型和观测值较为符合实际,而在载体发生强机动、跳动、侧滑时,其模型和观测值可信度较低;对于零速修正,则需要准确地探测出零速历元,误判会严重影响滤波结果。因此,在多源信息融合的联邦滤波器中,需要考虑子系统数学模型和观测值质量的影响而自适应地确定信息分配系数。

在估计理论中,验后残差反映了估计结果的好坏[18],但其计算具有滞后性。而在Kalman滤波中,新息单位权中误差的计算无需利用验后信息,同时可以证明,新息单位权中误差与验后残差平方和等价[19],因此新息单位权中误差[18]可以表达为

(4)

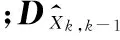
式(4)的计算只需要验前信息,可以每次滤波前计算,令分配系数βi=σ0,则

(5)

文献[20]从理论上证明了联邦滤波和自适应滤波的等效性,因此可以利用自适应滤波的原理对联邦滤波的分配系数进行确定[21-22];同时,利用抗差自适应滤波的权函数对自适应滤波进行调整[23],可得

(6)

式中,c1,c2的取值依据经验选取,一般而言c1取值为0.9左右,c2则可取10左右。

4 测试与分析

测试数据采用NovAtel SPAN系统采集,包含一台战术级IMU(iMAR FSAS,零偏小于0.75°/h,完整参数见文献[24])和一台双频测量型GPS接收机(NovAtel SPAN-SE),基站采用NovAtel OEM6接收机。IMU数据采样率为200 Hz,GPS数据采样率为1 Hz。数据采集于武汉市郊区,整体观测环境较好,基线长度不超过7 km,数据轨迹和整段数据的可视卫星数、位置精度因子(positional dilution of precision,PDOP)及双差模糊度固定情况如图3所示。整段数据的平均可视卫星数和PDOP分别为10和1.3,且双差模糊度全部固定,GPS定位结果可达厘米级。里程计观测值由GPS测速结果进行模拟,其噪声标准差为(0.1 m/s)。测试结果以IE(Inertial Explorer 8.30)GNSS/SINS双向平滑紧组合解算结果作为参考真值。

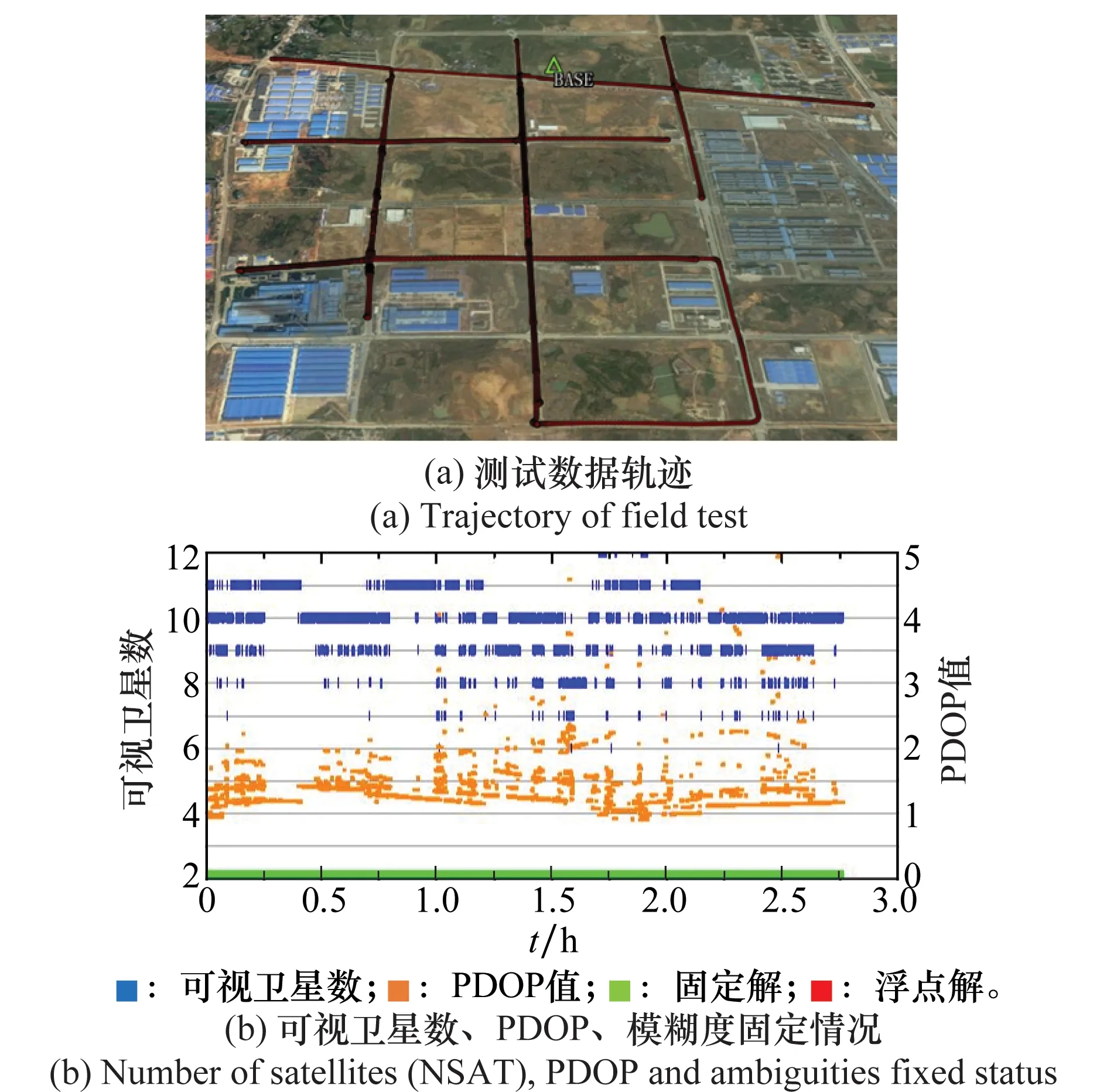
图3 测试数据轨迹及观测条件Fig.3 Trajectory of field test and observation condition

4.1 测试1

在GNSS观测值,OD观测值,零速探测结果上加入粗差,分别采用自适应联邦滤波(方法1)和传统的联邦滤波(方法2)进行解算。

图4、图5给出了采用两种解算方法的位置误差和速度误差。图4、图5中用灰色框分成了三部分:第一部分模拟了GNSS位置和速度误差,第二部分模拟了里程计误差,第三部分模拟零速误差。从图中可以看出自适应联邦滤波相对于传统联邦滤波而言,可以有效抵御观测值粗差的结果的影响,位置误差从超过2 m减小到0.2 m以内。速度误差与位置误差一致,最大速度误差从超过0.4 m/s减小到0.05 m/s以内。

图4 不同解算方法的位置误差(测试1)Fig.4 Position errors of different schemes (test 1)

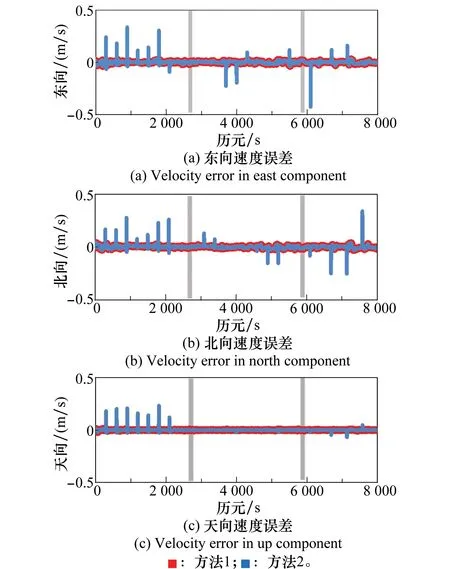
图5 不同解算方法的速度误差Fig.5 Velocity errors of different schemes

图6为采用两种解算方法的姿态误差。从图6可以看出,采用自适应联邦滤波后,航向角误差从0.3°减小到0.1°,水平姿态角则从0.2°左右减小到0.05°以内。同时可以看出,GNSS位置和速度观测粗差对航向角的干扰较强,里程计和零速修正则较弱,这与不同观测信息对航向角的可观测性强弱有关。

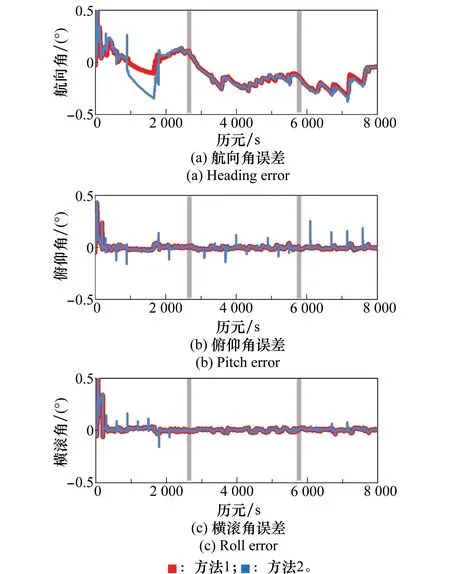
图6 不同解算方法的姿态误差Fig.6 Attitude errors of different schemes

图7给出了采用自适应联邦滤波的分配系数,其中图7(a)的红色曲线为位置更新的新息单位权中误差σ0。可以看到,当出现粗差时,σ0会急剧变大,此时由式(6)中的第三部分可知,该观测信息的分配系数为零(图中出现粗差的历元分配系数为0,且与σ0突变处重合),即该观测值不参与更新,这是自适应联邦滤波能抵御观测粗差的主要原因。同时,在图7(b)中可以看到,总体而言GNSS速度观测值分配系数比里程计的分配系数大,且里程计出现了较多的拒绝情况,这与两者的精度差异是相符合的。

4.2 测试2

为了验证本文的自适应联邦滤波算法对动态模型误差的容错性能,在740～800 s共60 s历元区间内模拟观测模型偏差。分别采用自适应联邦滤波(方法1)和传统的联邦滤波(方法2)进行解算。图8为采用两种解算方法的位置误差。

从图8可以看出,在进行多源信息融合时,相较于传统联邦滤波,自适应联邦滤波解算时可以更有效地抵御动态模型粗差对结果的干扰。对加入模型的历元区间的结果进行统计,位置误差RMS从(3.16E-1,8.10E-2,5.52E-2)减小到(2.32E-2,5.50E-3,2.05E-2),分别减小92%,93%和63%。

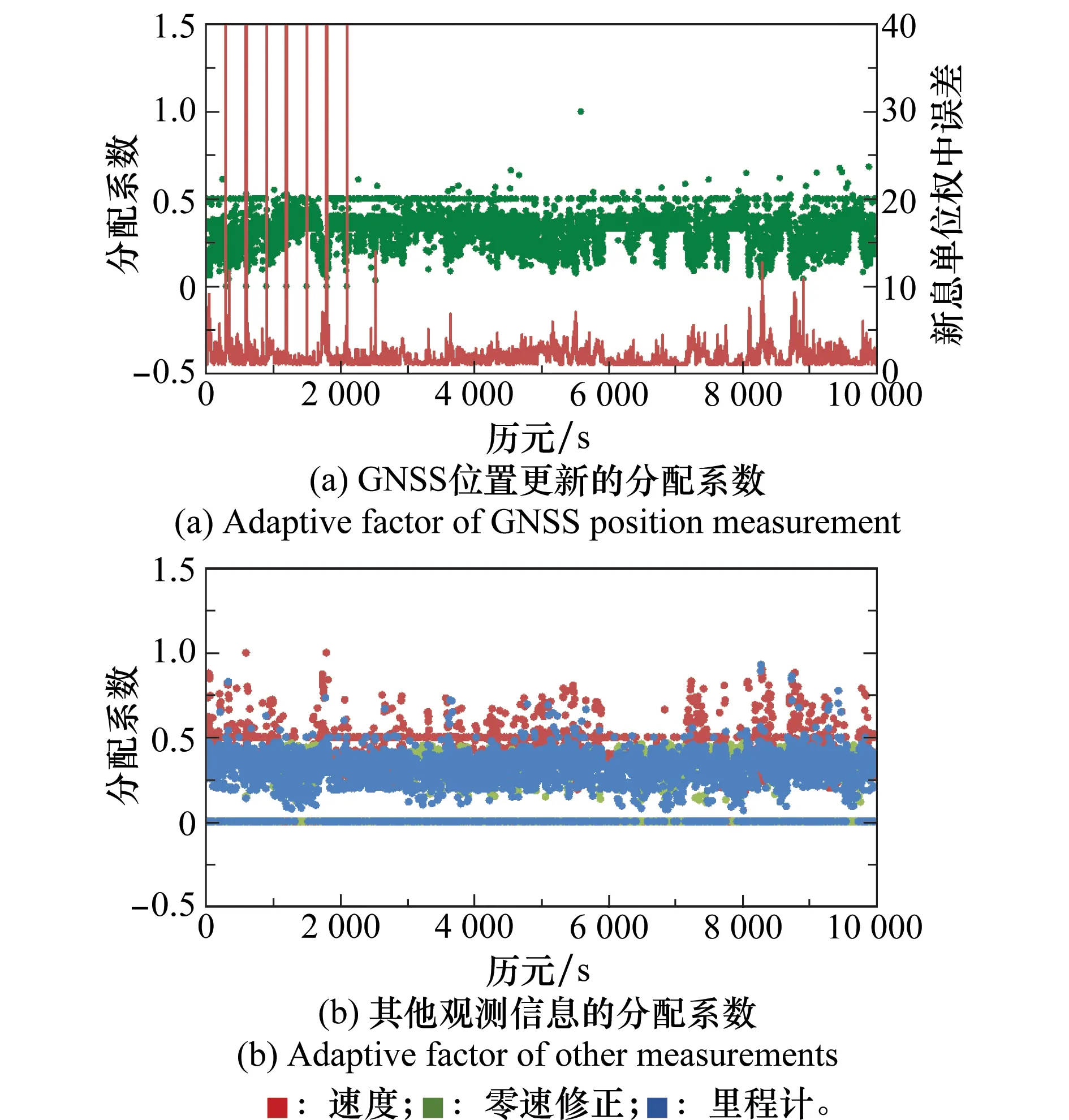
图7 自适应分配系数Fig.7 Adaptive factor of multi-sources measurements

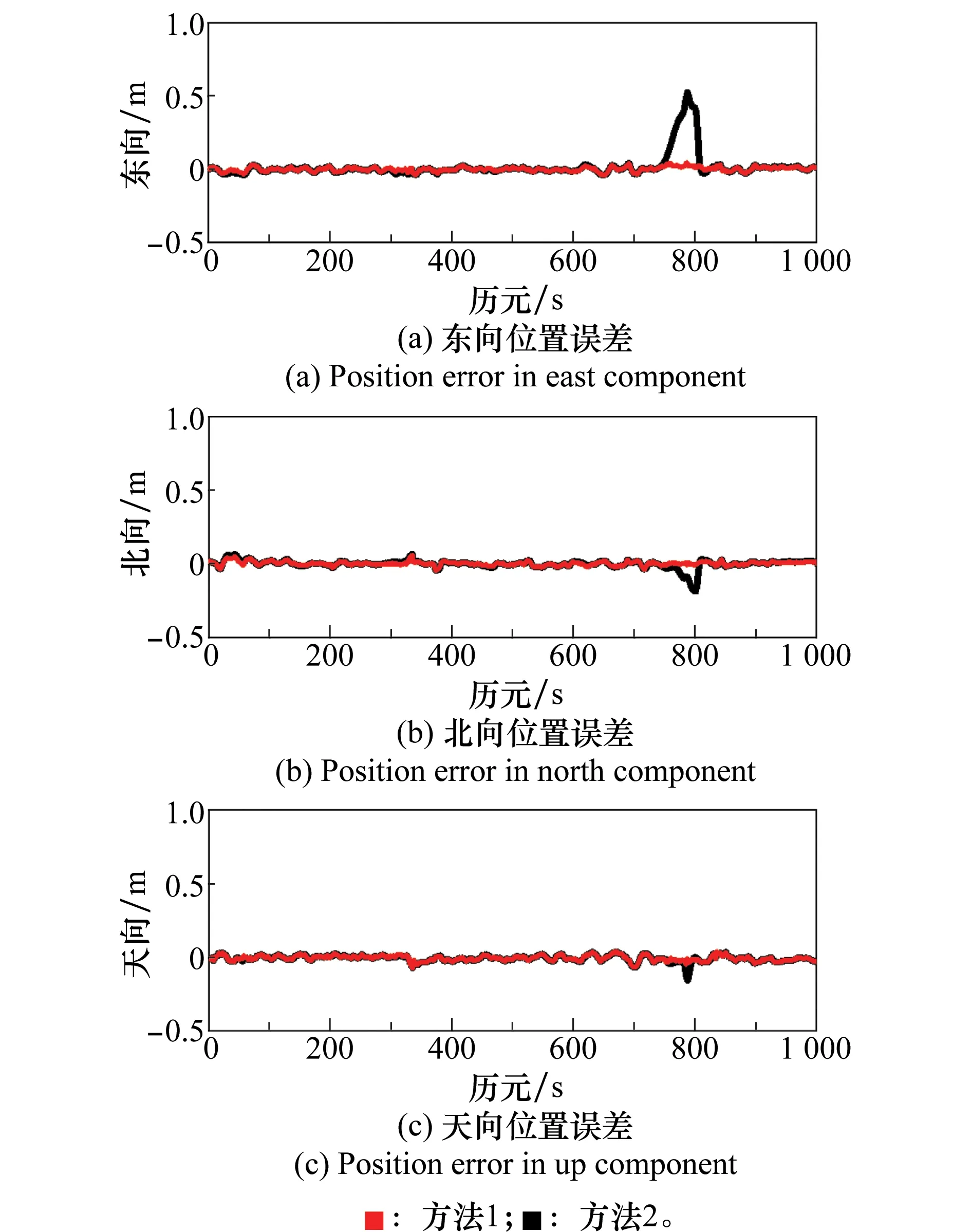
图8 不同解算方法的位置误差(测试2)Fig.8 Position errors of different schemes (test 2)

第3节提到,自适应滤波和联邦滤波在理论上具有等效性,采用式(6)对联邦滤波的信息分配系数进行调整时,等效于采用自适应滤波器进行解算,而自适应滤波可以抑制由于模型不准确引起的误差[22]。因此,在多源信息融合导航系统中,采用自适应联邦滤波可以提高动态模型偏差存在时的解算精度。

5 结 论

在多源信息融合时,由于数学模型偏差和观测粗差的存在,采用传统的联邦滤波往往容错性能不佳,使融合结果精度较差。本文研究了采用自适应联邦滤波对多源信息融合的方法,针对Kalman滤波中新息单位权中误差与验后残差平方和等价的特点,采用验前信息计算联邦滤波的分配系数,并借助自适应滤波原理对分配系数进行调整,得到了自适应联邦滤波的模型。利用该模型对组合导航的多源信息进行融合时,可以有效降低观测值粗差和数学模型偏差对滤波的干扰,提高了多源信息融合的解算精度。

[1] GROVES P D. Principles of GNSS, inertial, and multi-sensor integrated navigation systems[M]. 2nd ed. Boston/London: Artech House, 2013.

[2] SKALOUD J. Direct GEO-referencing in aerial photogrammetric mapping[J]. Photogrammetric Engineering & Remote Sensing, 2002, 68(3):207-210.

[3] KIM S B, BAZIN J C, LEE H K, et al. Ground vehicle navigation in harsh urban conditions by integrating inertial navigation system, global positioning system, odometer and vision data[J]. IET Radar, Sonar & Navigation, 2011, 5(8):814-823.

[4] LI X, MAO Y, LING X, et al. Applications of zero-velocity detector and Kalman filter in zero velocity update for inertial navigation system[C]∥Proc.of the IEEE Guidance, Navigation and Control Conference, 2014:1760-1763.

[5] WON D, AHN J, SUNG S, et al. Performance improvement of inertial navigation system by using magnetometer with vehicle dynamic constraints[J]. Journal of Sensors, 2015, 2015:1-11.

[6] ILYAS M, PARK S, BAEG S H. Improving unmanned ground vehicle navigation by exploiting virtual sensors and multi-sensor fusion[J]. Journal of Mechanical Science & Technology, 2014, 28(11):4369-4379.

[7] 秦永元,张洪钺,汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 1998.

QIN Y Y, ZHANG H Y, WANG S H. Kalman filter and the theory of integrated navigation[M]. Xi’an: Northwestern Polytechnical University Press, 1998.

[8] GENG K K, CHULIN N A. Applications of multi-height sensors data fusion and fault-tolerant Kalman filter in integrated navigation system of UAV[J].Procedia Computer Science, 2017, 103: 231-238.

[9] 房建成,李学恩,申功勋. INS/CNS/GPS智能容错导航系统研究[J]. 中国惯性技术学报, 1999(1): 5-8.

FANG J C, LI X E, SHENG G X. Research on INS/CNS/GPS Intelligent fault tolerant navigation system[J]. Journal of Chinese Inertial Technology,1999(1): 5-8.

[10] CUI P, XU T. Data fusion algorithm for INS/GPS/Odometer integrated navigation system[C]∥Proc.of the 2nd IEEE Conference on Industrial Electronics and Applications,2007:1893-897.

[11] DENG H, LIU G, CHEN H, et al. The application of federated Kalman filtering in SINS/GPS/CNS integrated navigation system[J]. International Journal of Wireless & Microwave Technologies, 2012, 2(2):12-19.

[12] ZHANG H, LENNOX B, GOULDING P R, et al. Adaptive information sharing factors in federated Kalman filtering[J].IFAC Proceedings Volumes, 2002, 35(1): 79-84.

[13] WANG Q, CUI X, LI Y, et al. Performance enhancement of a USV INS/CNS/DVL integration navigation system based on an adaptive information sharing factor federated filter[J]. Sensors, 2017, 17(2):239.

[14] HU H, HUANG X, LI M, et al. Federated unscented particle filtering algorithm for SINS/CNS/GPS system[J]. Journal of Central South University of Technology,2010,17(4):778-785.

[15] WEI Q, FANG J C. Research on FKF method based on an improved genetic algorithm for multi-sensor integrated navigation system[J]. Journal of Navigation, 2012, 65(3): 495-511.

[16] 朱锋.PPP/SINS组合导航关键技术与算法实现[D].武汉:武汉大学, 2015.

ZHU F. The key technology and algorithm of PPP/SINS integration[D].Wuhan: Wuhan University, 2015.

[17] NIU X, NASSAR S, EL-SHEIMY N. An accurate land-vehicle MEMS IMU/GPS navigation system using 3D auxiliary velocity updates[J]. Navigation, 2007, 54(3): 177-188.

[18] 崔希璋,於宗俦,陶本藻,等. 广义测量平差[M].2版.武汉:武汉大学出版社, 2009.

CUI X Z, YU Z C, TAO B Z, et al. Generalized surveying adjustment[M]. 2nd ed. Wuhan: Wuhan University Press, 2009.

[19] 陶本藻.卡尔曼滤波模型误差的识别[J].大地测量与地球动力学,1999,19(4):15-20.

TAO B Z. Identification of Kalman filtering model errors[J]. Crustal Deformation and Earthquake, 1999, 19(4):15-20.

[20] LI Z K, GAO J X, WANG J, et al. PPP/INS tightly coupled navigation using adaptive federated filter[J]. GPS Solutions, 2017,21(1):1-12.

[21] YANG Y X, GAO W G. An optimal adaptive Kalman filter[J]. Journal of Geodesy, 2006, 80(4):177-183.

[22] YANG Y X, CUI X Q, GAO W G. Adaptive integrated navigation for multi-sensor adjustment outputs[J]. Journal of Navigation, 2004, 57(2): 287-295.

[23] YANG Y X, GAO W G, ZHANG X. Robust Kalman filtering with constraints: a case study for integrated navigation[J]. Journal of Geodesy, 2010, 84(6): 373-381.

[24] NOVATEL INC. SPAN IMU-FSAS: tactical grade, low noise IMU combines with NovAtel's GNSS technology to create a 3D position, velocity and attitude solution[EB/OL].[2017-08-25].https:∥www.novatel.com/assets/Documents/Papers/FSAS.pdf.