基于单元相关的GPS L1C/A与L1C联合捕获算法

纪元法, 刘 媛, 孙希延, 蔚保国, 甄卫民

(1. 桂林电子科技大学广西精密导航技术与应用重点实验室, 广西 桂林 541000;2. 卫星导航系统与装备技术国家重点实验室, 河北 石家庄 050000;3. 电波环境特性及模化技术重点实验室, 山东 青岛 266000)

0 引 言

目前,L1频段是唯一具有两个不同全球定位系统(global positioning system,GPS)民用信号的频带,即GPS用户将可以在同一频率接收传统L1C/A码信号和新型L1C信号[1]。GPS L1C/A码信号采用二进制相移键控(binary phase shift keying,BPSK)调制,L1C信号具有导频和数据双通道结构,其中数据通道采用BOC(1,1)调制,导频通道采用TMBOC(6,1,4/33)调制[2]。同频L1C/A和L1C信号所调制的导航电文信息是同步的,且L1C/A的码延迟和L1C信号数据码、导频码的码延迟是相同的[3]。GPS L1C/A和L1C信号的联合捕获,不仅充分利用信号能量,以有限的接收机附加复杂度提高捕获灵敏度,而且可借助二进制偏移载波(binary offset carrier,BOC)调制信号窄相关峰的优点,提高捕获精度[4]。但由于L1C/A码的周期为1 ms,L1C信号的周期为10 ms,传统联合捕获得到的检测量存在9个次峰,易导致误捕的问题[5-6]。已有的联合捕获方案主要分为3类:一是L1C的导频分量与L1C/A码信号的双通道联合捕获,如文献[7]中,利用相干的方法,将本地导频码和C/A码分别与接收信号做相关,得到较尖锐的检测峰,但该方法浪费了L1C信号数据通道的能量,无法体现新型民用L1C信号双通道的结构优势,且次峰与主峰的峰峰比达到50.96%;二是三通道的联合捕获,如文献[8]中,本地L1C数据码、导频码和L1C/A码分别与接收信号做相关,检测量取3个通道的平方和,充分利用了信号的能量,但次峰抑制效果不明显,且硬件资源消耗较多；三是单通道的联合捕获,如文献[9]中,使用C/A码、L1C导频与数据码的线性组合生成本地复合码,在单通道内实现捕获,节省了硬件资源,得到相关峰的跨度为1码片,但该方法仍没有完全消除次峰。

本文首先给出L1 C/A和L1C复合信号的数学模型,基于单元相关的方法对GPS L1 C/A码和L1C信号联合捕获,将本地L1C/A和L1C序列分别拆分为奇、偶两个单元信号,对单元信号与接收信号的单元相关函数进行重组,再将两个重组相关函数相乘,实现信号能量的叠加,提高主峰峰值,得到尖锐的窄相关峰,达到更好的捕获性能。

1 基于单元相关的L1C/A-L1C联合捕获算法

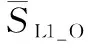
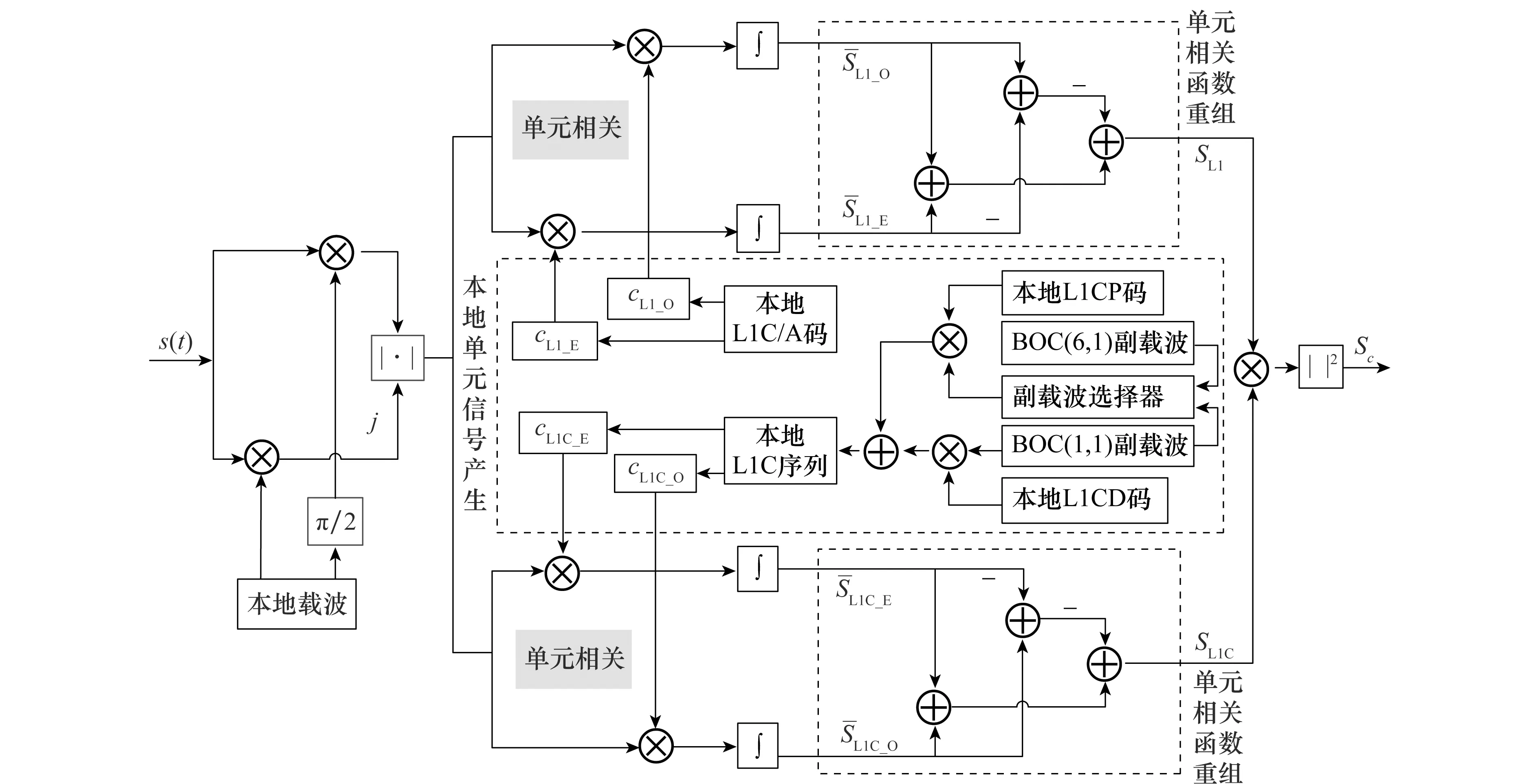
图1 基于单元相关的GPS L1C/A与L1C联合捕获算法原理图Fig.1 Block diagram of L1C/A-L1C combined acquisition algorithm based on unit correlation

由于L1C信号的载波相位与L1P(Y)军用信号相同,因此L1C数据与导频分量相对L1C/A码信号相位正交,L1 C/A和L1C复合信号的数学模型[10]如下:

cos(2π(fIF+fd)t+θ)+

(1)

式中,C为复合信号的总功率；功率分配参数[11]α=0.439 1,β=0.146 4,γ=0.414 5;dP(t)为L1C导频通道的次级码;dD(t)和dC/A(t)分别为L1C与L1C/A的导航电文;cP(t)、cD(t)和cC/A(t)分别为导频码、数据码和L1C/A码序列;gP(t)和gD(t)为L1C导频和数据分量的副载波;τ和fd是接收信号的码延迟和多普勒频率;fIF为信号的中频;θ是载波相位常量。

L1C/A码、L1C导频分量测距码和数据分量测距码的数学模型可表示为

(2)

(3)

(4)

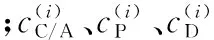
L1C数据通道采用BOC(1,1)调制,导频通道采用TMBOC(6,1,4/33)调制,BOC(1,1)和BOC(6,1)的子载波数学模型可表示为

(6)

(7)

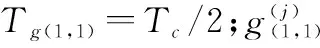
利用上述数学模型,产生本地L1C序列:

cL1C(t)=cL1CD(t)+cL1CP(t)

(8)

(9)

cL1CP(t)=

(10)

式中,cL1CD为经BOC(1,1)调制的数据码；cL1CP为经TMBOC(6,1,4/33)调制的导频码。

以BOC(1,1)子载波脉冲长度为基准,将本地L1C/A码序列的每个码片等分成两部分,依次截取每个码片第一等份的信息,组成奇单元信号cL1_O(t),每个码片第二等份的信息组成偶单元信号cL1_E(t):

(12)

(13)

同样,将本地L1C序列拆分为奇、偶两个单元信号:

cL1C_O(t)=cP_O(t)+cD_O(t)

(15)

cL1C_E(t)=cP_E(t)+cD_E(t)

(16)

式中,cD_O(t)和cD_E(t)为本地数据分量拆分得到的奇、偶两部分;cP_O(t)和cP_E(t)为本地导频分量拆分得到:

(17)

(18)

cP_O(t)=

(19)

cP_E(t)=

(20)

输入信号经过与本地载波混频,与本地L1和L1C拆分得到的奇、偶单元信号相乘,经积分处理后输出:

[cos(πΔfdTs+Δθ)+sin(πΔfdTs+Δθ)]+NL1_O

(21)

[cos(πΔfdTs+Δθ)+sin(πΔfdTs+Δθ)]+NL1_E

(22)

[cos(πΔfdTs+Δθ)+sin(πΔfdTs+Δθ)]+

βCRP_O(Δτ)dPTssinc(πΔfdTs)·

[cos(πΔfdTs+Δθ)+sin(πΔfdTs+Δθ)]+NL1C_O

(23)

[cos(πΔfdTs+Δθ)+sin(πΔfdTs+Δθ)]+

βCRP_E(Δτ)dPTssinc(πΔfdTs)·

[cos(πΔfdTs+Δθ)+sin(πΔfdTs+Δθ)]+NL1C_E

(24)

式中,RL1_O、RL1_E、RD_O、RD_E、RP_O和RP_E为本地单元信号与接收信号的单元相关函数;Δτ为码相位偏差;Δfd为多普勒残差;Δθ为载波相位误差;NL1_O、NL1_E、NL1C_O、NL1C_E为服从均值为0,方差为σ2的高斯噪声。积分处理后的结果可简化为

(25)

(26)

(27)

(28)

(29)

(30)

再将上述两检测量相乘,取模平方得到最终的检测量:

Sc=|SL1SL1C|2

(31)

由于每比特导航电文和次级码片对应一个周期的测距码[12],假设在积分时间10 ms内没有导航数据和次级码符号跳变,dC/A、dD、dP为常量可以省去,最终检测量中的SL1SL1C可化简为

Sc1=SL1SL1C=(CTsRL1(Δτ)+NL1)(CTsRL1C(Δτ)+NL1C)=

CTsRL1C(Δτ)NL1sin(2Δθ)+NL1NL1C

(32)

式中,RL1和RL1C分别为L1C/A码和L1C码的重组相关函数:

RL1(Δτ)=γ[|RL1_O(Δτ)+RL1_E(Δτ)|-

|RL1_O(Δτ)-RL1_E(Δτ)|]

(33)

RL1C(Δτ)=αRP(Δτ)+βRD(Δτ)=

α[|RP_O(Δτ)+RP_E(Δτ)|-|RP_O(Δτ)-RP_E(Δτ)|]+

β[|RD_O(Δτ)+RP_E(Δτ)|-|RD_O(Δτ)-RP_E(Δτ)|]

(34)

设置码延迟τ=600,码相位偏差Δτ=0,基于Matlab仿真单元相关法产生重组相关函数RL1和RL1C的过程如图2和图3所示,最终检测量的相关函数R=RL1RL1C如图4所示。

图2 L1C重组相关函数的产生Fig.2 Generation of L1C reconstructed correlation function

图3 L1C/A码重组相关函数的产生Fig.3 Generation of reconstructed correlation function of L1C/A code

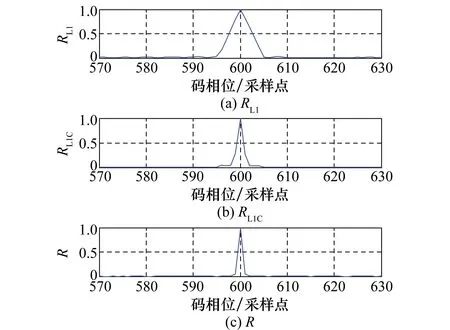
图4 最终检测量的相关函数产生Fig.4 Generation of correlation function of detection variable

2 算法性能分析

分别提取Sc1中的纯信号项、纯噪声项和交叉项:

(35)

V=NL1NL1C

(36)

H=(CTsRL1(Δτ)NL1C+CTsRL1C(Δτ)NL1)·

(sin(Δθ)+cos(Δθ))

(37)

噪声项NL1与NL1C是不相关的高斯白噪声,均值为0,方差为σ2。假设Δθ=0,则纯噪声项V服从正态乘积分布[13],其概率密度函数如下:

(38)

(39)

式中,KV(·)为第二类V阶修正贝塞尔函数;Γ(·)为伽玛函数;则V的方差为

(40)

交叉项H仍然服从高斯分布,其方差为

(41)

综上,Sc1是高斯噪声与常量的累加,亦服从均值为E(Sc1),方差为D(Sc1)的高斯分布:

(42)

D(Sc1)=σ4+σ2[CTs(RL1(Δτ)+RL1C(Δτ))·

(sin(Δθ)+cos(Δθ))]

(43)

假设只有噪声存在的情况为X0,既有信号又有噪声存在的情况为X1。在X0情况下,检测量Sc为均值为0,方差为σ4高斯变量的平方,服从中心χ2分布[14],概率密度函数为

(44)

(45)

在X1情况下,检测量Sc为均值为E(Sc1),方差为D(Sc1)高斯变量的平方,服从非中心χ2分布[15],概率密度函数为

(46)

假设相干积分时间为10 ms,虚警概率Pfa=10-3,单元相关法的联合捕获、单通道联合捕获、单L1C和单L1C/A码信号捕获的检测概率随载噪比变化如图5所示。在载噪比为27 dBHz的环境下,单L1C和单L1C/A信号捕获的检测概率均小于10%,而两种联合捕获方法的检测概率均高于90%,远远优于单个信号的捕获。若以90%的检测概率为标准,单元相关法的联合捕获能检测到载噪比约为25 dBHz的信号,单通道联合捕获能检测到载噪比约为27 dBHz的信号,捕获灵敏度约提高2 dBHz。

图5 检测概率随载噪比变化曲线Fig.5 Curve of detection probability varies with carrier to noise ratio

3 仿真结果及分析

基于Matlab平台仿真实现基于单元相关的GPS L1C/A和L1C信号联合捕获算法,设置输入复合信号的中频为4.309 MHz,相干积分时间为10 ms,采样率取10.23 MHz,多普勒搜索范围为[-5 kHz,5 kHz],接收信号多普勒为2 000 Hz,码偏移为600采样点,多普勒步进为500 Hz,载噪比为27 dBHz时的捕获结果如图6所示。

图6 单元相关法的联捕结果Fig.6 Combined acquisition result of unit correlation

捕获得到检测峰所在的码相位为第600个采样点,多普勒为第15个频点,即2 000 Hz,与输入信号的预设值相同。

图7为载噪比27 dBHz的环境下,单元相关法、单通道、双通道和三通道联合捕获的二维结果图,从码相位一维的捕获结果可以看出,后3种联合捕获方法均存在9个次峰,峰峰比分别为27.06%、50.96%、40.78%,这是因为L1C/A码的周期是1 ms,根据伪随机码的强自相关性,10 ms的相干积分将带来9个次峰。双通道和三通道联捕方案均取各通道检测量的平方和,没有达到很好的抑制次峰的效果。单元相关法取两通道检测量乘积的平方,不仅充分叠加主峰的能量,并且完全地消除次峰,大大降低误捕的概率。

图7 4种联合捕获次峰对比Fig.7 Comparison of sub-peaks of four combined acquisition algorithms

图8为载噪比27 dBHz的环境下,单元相关法、单通道、双通道和三通道联合捕获的相关峰跨度对比图。

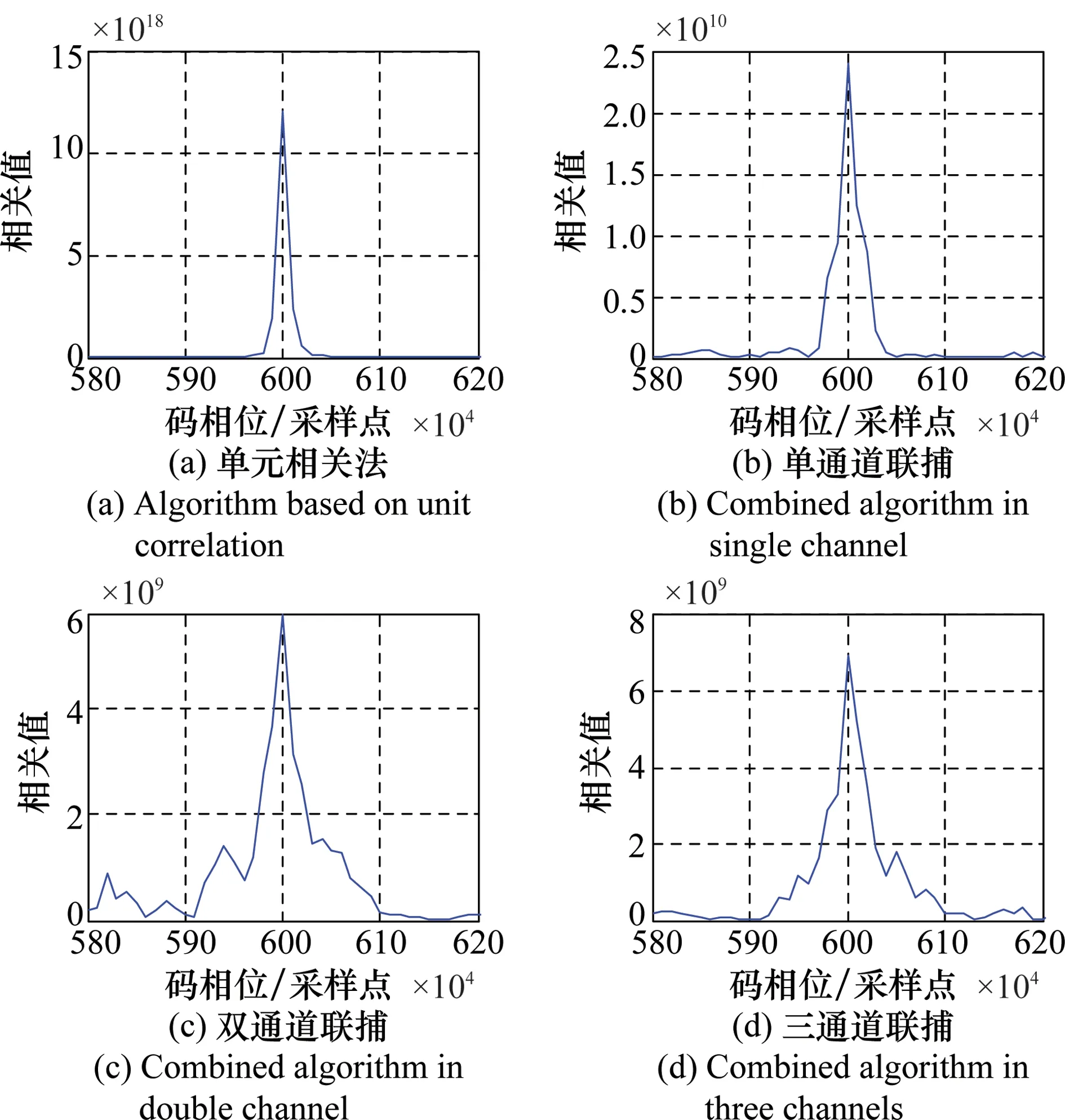
图8 相关峰跨度对比Fig.8 Comparison of span of correlation peaks

仿真结果表明,若取最大相关值作为门限,4种方法捕获的码相位均为第600采样点,与输入信号的预设参数一致。但双通道和三通道联合捕获的相关峰跨度均约为2个码片,没有体现BOC调制信号可高精度捕获的优点,单元相关法的相关峰跨度约为0.5码片,较单通道、双通道和三通道联合捕获的跨度分别减小约0.5码片、1.5码片、1.5码片,大大提高捕获精度。

4 结 论

本文提出基于单元相关的GPS L1C/A与L1C联合捕获技术,将本地L1C/A码和L1C序列分别拆分为奇、偶两个单元信号,对单元信号与接收信号的单元相关函数进行重组,得到最终检测量的主峰跨度为0.5个码片,较单通道、双通道和三通道联合捕获相关峰的跨度分别减小约0.5码片、1.5码片、1.5码片,大大提高捕获精度;且该算法能完全消除L1C/A码信号引起的9个次峰,降低误捕概率,捕获灵敏度比单通道的联捕方法,提高约2 dBHz,因此该方法在弱信号捕获时优势更加明显。

[1] BETZ J W, BLANCO M A, CAHN C R, et al. Description of the L1C signal[C]∥Proc.of the 19th International Technical Meeting of the Satellite Division of the Institute of Navigation, 2006: 2080-2091.

[2] STANSELL T A, HUDNUT K W, KEEGAN R G. GPS L1C: enhanced performance, receiver design suggestions, and key contributions[J]. Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation, 2010, 7672(6): 2860-2873.

[3] YUAN H, LV J, YU Y, et al. a fast acquisition algorithm for L1C based on L1CA and L1C combined detection[C]∥Proc.of the China Satellite Navigation Conference, 2012: 689-698.

[4] LEE C, CHEN Y H, WONG G, et al. Multipath benefits of BOC vs. BPSK modulated signals using on-air measurements[C]∥Proc.of the Institute of Navigation ITM Conference, 2013: 742-751.

[5] GERNOT C, O’KEEFE K, LACHAPELLE G. Assessing three new GPS combined L1/L2C acquisition methods[J]. IEEE Trans.on Aerospace and Electronic Systems,2011,47(3):2239-2247.

[6] BORIO D, O’DRISCOLL C, LACHAPELLE G. Coherent, noncoherent, and differentially coherent combining techniques for acquisition of new composite GNSS signals[J]. IEEE Trans.on Aerospace and Electronic Systems,2009,45(3):1227-1240.

[7] SHANMUGAM S K. New enhanced sensitivity detection techniques for GPS L1C/A and modernized signal acquisition[D]. Calgary: University of Calgary, 2008.

[8] SEALS K C, MICHALSON W R, SWASZEK P F, et al. Using both GPS L1 C/A and L1C: strategies to improve acquisition sensitivity[C]∥Proc.of the International Technical Meeting of the Satellite Division of the Institute of Navigation,2013:92-106.

[9] MACCHIGERNOT F, PETOVELLO M G, LACHAPELLE G. Combined acquisition and tracking methods for GPS L1C/A and L1C signals[J]. International Journal of Navigation and Observation, 2010(2010): 1-19.

[10] IS-GPS-200E.Navstar GPS space segment/navigation user interfaces[S]. U.S.:[s.n.], 2010.

[11] CHEN Y H, LO S, ENGE P, et al. Combining L1 signals for improved sensitivity[C]∥Proc.of the International Technical Meeting of the Institute of Navigation, 2015: 164-172.

[12] ZHOU J, LIU C. Joint data-pilot acquisition of GPS L1 civil signal[C]∥Proc.of the IEEE International Conference on Signal, 2015: 1628-1631.

[13] WANG H, JI Y, SHI H, et al. The performance analysis of unambiguous acquisition methods for BOC(m,n) modulated signals[C]∥IEEE International Conference on Wireless Communications, Networking and Mobile Computing, 2011: 1-4.

[14] O’DRISCOLL C. Performance analysis of the parallel acquisition of weak GPS signals[J]. Journal of Northeast Petroleum University, 2007, 31(8): 17-21.

[15] MUBARAK O M. Performance comparison of multipath detection using early late phase in BPSK and BOC modulated signals[C]∥IEEE International Conference on Signal Processing and Communication Systems, 2014: 1-7.