齐次化思想在解题中的应用*

广东省兴宁市第一中学(514500) 蓝云波 邬海辉 刘宇峰

在数学中,我们把一个多项式或分式中各个单项式的次数都相同的式子,称之为齐次式.由于齐次式各项的次数相同,因而具有对称美和结构美的特征,这使得问题的处理往往会更容易、更简洁、更有规律.同时,对于一些涉及非齐次式的数学问题,如果我们能够结合题设条件,将非齐次式问题转化为齐次式问题来处理,则往往能化难为易、化繁为简,并达到优化解题的过程,起到事半功倍的效果.我们把这种非齐次式问题转化为齐次式问题的思想叫做齐次化思想.齐次化思想是数学中的重要思想方法,在解题中具有举足轻重的地位,在各类考试中有较为广泛的应用.下面笔者以近年来的各类试题为例,从多个视角谈谈齐次化思想在解题中的应用.现分析如下,供大家参考并斧正.

1.三角函数问题

在高中数学中,在教材中明显体现出齐次化思想的是人教A版必修4第一章《三角函数》中的第22页B组习题里的一道习题:已知tanα=2,求的值.此题所求的分式中的分子和分母是一个关于sinα,cosα的一次齐次式.结合已知条件,我们可以在分子和分母中同除以cosα,转化为一个关于tanα的式子,通过这样的处理,问题便迎刃而解.这说明,齐次化思想是源于课本的一种重要的思想方法.在高考中,这种思想也时常考查,如下面这一道高考试题.

例1(2015年高考广东卷) 已知tanα=2,

点评 本题的第二问表面上不是齐次式,但在通过化简和变形后,可化为一个关于sinα,cosα的二次齐次式.所用到的思想方法和课本上的习题如出一辙.这体现出高考源于课本而高于课本的原则.也让我们感受到了齐次化思想的在处理这类问题中的优越性.

通过对例1的分析,我们发现,在使用齐次化思想把非齐次式转化为齐次式后,终极的目标是化多变量为单变量问题.如例1本来同时含有sinα,cosα,但在通过分子和分母同除以cosα之后,便转化成只含有tanα的式子.因此,齐次化以后的处理方法本质上其实是数学中的消参思想.

2.求取值范围

在一些代数问题中,我们常常要求解在某个条件下代数式的取值范围或最值.此时我们若能把所求的代数式设为一个变量,并把它看作参数,通过适当的方法代入已知条件中,并设法实现齐次化,问题便能实现较为快捷的解决.

例2(2016年河北省高中数学竞赛)实数x,y满足x2+y2+xy=3,则x2+y2的取值范围是.

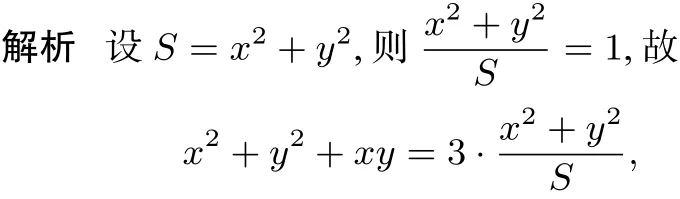
整理得(S-3)y2+Sxy+(S-3)x2=0.

①当x=0时,由x2+y2+xy=3得y2=3,此时S=x2+y2=3.

②当x/=0时,则S/=3时,方程(S-3)y2+Sxy+

(S-3)x2=0,可化为式为关于的一元二次方程,则有∆=S2-4(S-3)2≥0,即S2-8S+12≤0.结合S/=3,可解得2≤S≤6且S/=3.

由○①2知2≤S≤6,故x2+y2的取值范围是[2,6].

点评 本题的常见解法是利用基本不等式进行求解,解题的技巧性较强.而本题的关键是通过把已知条件并实现齐次化,然后利用整体思想,通过化双变量为单变量转化为一元二次方程有解问题,使问题的难度降低,并可快速求出答案.

3.解析几何问题

离心率问题是解析几何中的核心考点,由椭圆与双曲线的离心率公式e=可知,若能在解n题中,设法构建出关于a,c的n次齐次式,然后再同除以a,离心率问题便能快速实现解决.

因为点(-1,0)到直线l的距离

所以

点评 本题是经典的可构造齐次式解决离心率的问题,通过消去b,并构建不等式,得到一个关于a,c的四次齐次式,然后同除以a4,转化为单变量问题,问题便迎刃而解.

众所周知,在各类考试中,解析几何解答题通常以运算量大著称,解题的最核心的思想方法是设而不求,在涉及直线与圆锥曲线的位置关系的问题中,常见的做法是联立直线与曲线的方程组,进行消元,以达到设而不求的目的.若我们在联立方程组时,不实施消元,而是通过实施齐次化思想,化为齐次方程实施设而不求,往往会达到意想不到的效果.

例4(2015年广东省高中数学联赛)设抛物线y2=2px(p＞0)上有两个动点A(x1,y1)(y1＞0),B(x2,y2)(y2＜0).

(1)设直线AB的连线与x轴交于C,抛物线在A、B的切线的交点坐标D(x3,y3),证明:|OD|+x3=0,其中O为坐标原点;

(2)若OA⊥OB,求线段AB的中点的轨迹方程.

解析 (1)略; (2)设AB中点为M(x0,y0),直线AB方程为mx+ny=1,联立齐次化可得韦达定理可得-2mp=-1,即m=所以直线AB恒过定点(2p,0).以下对直线的斜率分两种情形讨论:

②若直线AB斜率不存在,此时M的坐标为(2p,0),它显然满足y20=p(x0-2p).

综上所述,AB中点轨迹方程为y2=p(x-2p).

点评 本题通过使用齐次化思想,可以大幅减低运算量,提高解题效率.笔者发现,构造齐次式是解答解析几何题的一大利器,具有一定的通性通法,这使我们再次感受到齐次化思想在解题中的独特魅力,与独特视角,能杀敌于无形之中,令人耳目一新！

4.证明不等式

不等式的证明是高中数学竞赛的重要考点,具有举足轻重的地位.由于其方法繁多,技巧性极强,因此通常难度较大.在不等式的证明方法中,齐次化思想是一种较为重要的方法,通过齐次化处理,使得不等式更完美,更对称,使得问题的难度降低,从而有利于问题的求解.

例5(2014年全国高中数学联赛二试)设实数a,b,c满足a+b+c=1,abc＞0.求证:ab+bc+ca

证明 不妨设a≥b≥c.(1)若c＞0,因为a+b+c=1,故(a+b+c)2=a2+b2+c2+2ab+2bc+2ca=1,原不等式等价于即等价于的齐次式:

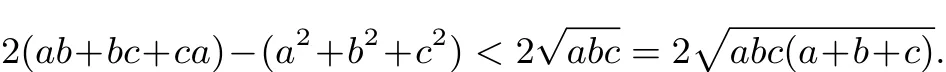
若2(ab+bc+ca)≤(a2+b2+c2),原不等式显然成立;若2(ab+bc+ca)＞(a2+b2+c2),两边平方后等价于

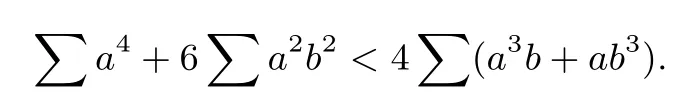
注意到故有

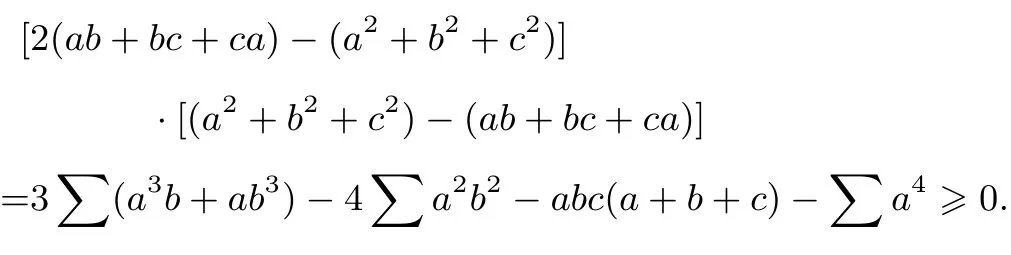
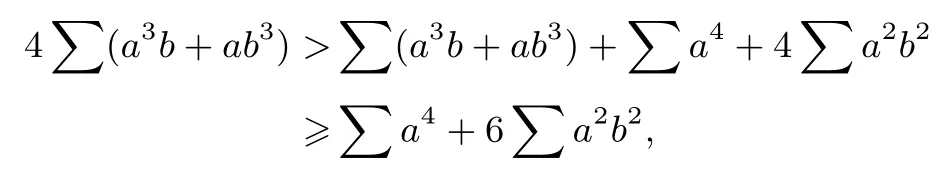
故原不等式成立.

(2)若c＜0,则b＜0,a＞0,

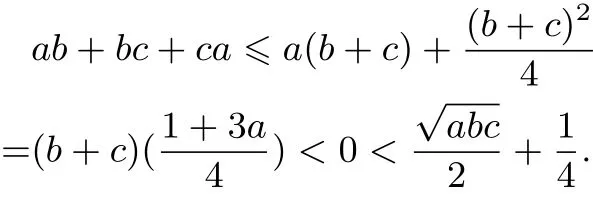
综上,原不等式得证.

点评 本题的难点在于c＞0时的证明,本文给出的解法的关键是通过a+b+c=1这个条件,并通过平方之后,从而使得所要证明的不等式化为一个四次齐次式,从而使问题的方向更明确.并最终实现问题的圆满解决.

5.证明数列不等式

前面所举的例题都是都过化为完全齐次式使问题得到巧妙的解决的.事实上,对于某些不能完全化为齐次式的问题,我们也可以利用相关的思想方法使问题得到完美的解决.这类问题,由于式子中只是部分齐次的,故我们可以称之为部分齐次问题.这样,我们可以把齐次化思想得到更为广泛的应用,下面我们看这道经典考题的独特的处理方法.

例6(2011年高考广东卷理科)设b＞0,数列an满足

(1)求数列an的通项公式;

若x＞1,不等式可化为

f(x)=x2n+1-(2n+1)xn+1+(2n+1)xn-1≥0(*)注意到f(1)=0,而

令g(x)=(2n+1)xn+1-(2n+1)(n+1)x+n(2n+1),且g(1)=0,g′(x)=(2n+1)(n+1)xn-(2n+1)(n+1)＞ 0,故g(x)在(1,+∞)上单调递增,所以g(x)＞ g(1)=0,故f′(x)＞ 0,故 f(x)在 (1,+∞)上单调递增,所以f(x)＞f(1)=0,所以(*)得证;若0＜x＜1,同理可证.

点评 本题官方给出的答案是利用试卷中给出的参考公式进行解答的,事实上,不用这个参考公式同样可以使问题得到解决.本题中,虽然不能化为完全的齐次式,但是通过观却是齐次式,故可将计就计,转化为用表示,从而实现问题维度的降低,最后再通过导数转化为一个简单的不等式的证明.

6.函数综合问题

近几年,随着高考的深入开展,函数与导数的问题兴起了双变量问题.对于这类问题,我们虽然也不能化为完全齐次式,但是却可化为部分齐次问题,下面我们来看下面这道典型的例题,让我们在例5的基础上,再次体会齐次化思想在不完全齐次式问题中的精彩应用.

(1)当m=-2时,求函数f(x)的所有零点;

(2)若f(x)有两个极值点x1,x2,且x1＜ x2,求证x1x2＞e2.

综上知,x1x2＞e2得证.

点评 本题以重要不等式—对数平均不等式为背景,考查了导数在研究函数中的综合运用,解题的关键在于对通过等价转化后,双变量的处理,解答过程使用了消元思想,解题的关键把右边局部是一个一次齐次式,在通过化为用表示的不等式后,要构造的函数便呼之欲出.需要注意的是,在近几年的各类考试中,以对数平均不等式为背景的试题屡见不鲜,且常考常新,应引起足够的重视.

通过以上的探索,我们可以发现,齐次化是源于课本的一种非常重要的数学思想方法.齐次化的本质其实就是通过代数变形,将二元化为一元,通过整体处理,从而达到减少字母量的效果,以此降低解题的维度与难度,从某种意义上也可以说是消参思想的延续.同时,我们还发现,齐次化不仅仅是一种解题策略,而且还能上升为一种解题思想,并指导我们更为高效地解决数学问题.并且在三角函数、代数式求取值范围(最值)、解析几何、证明代数不等式、证明数列不等式、函数与导数等方面具有着非常广泛的应用.

这说明,教师在平时的教学中,要重视对课本的理解和挖掘,并从中找出体现数学思想方法的据点,并传授给学生.对重要的数学思想,还应从不同角度呈现出来,以达到提高学生数学核心素养的目的,并提高教师的课堂教学的高效性.齐次化思想正是体现数学美、数学本质的重要载体,应引起足够的重视.