2017年福建省中考数学卷与课程标准的一致性研究

徐帆+黄莉+张胜元

1研究背景

福建省人民政府办公厅于2016年颁布的《福建省“十三五”教育发展专项规划》[1]，指出，为促进入学机会公平，完善中小学招生入学办法，从2017年起全省统一组织实施语文、数学、英语等科目中考，至此我省中考由各地市命题跨入全省统一命题新时代，具有开创性的意义，中考作为九年义务教育阶段的终结性考试，是初中学科学习目标评价的重要手段，也对今后初中教学具有导向作用.此外，检索已有的中考研究文献，表明中考与课程标准的一致性问题已是国内外研究的一个重要方向，特别是2017年作为全省中考统一命题的首年，其试卷的命制质量备受关注，而我国于2011年颁布的<义务教育数学课程标准》[2]（以下简称“课程标准”）作为一种纲领性文件，也是中考试卷命制的根本依据，因此，本文对2017年福建省中考数学卷与课程标准之间是否具有一致性进行研究，不仅可以体现试卷与课程标准的吻合程度，也可以帮助教师更好地理解课程标准、学业评价和课堂教学之间的联系，最大程度地利用课程标准来指导教学实践.

2一致性研究工具与过程

2.1 一致性研究对象

本文選取2017年福建省中考数学卷和国家教育部于2011年颁布的《义务教育数学课程标准》为研究对象。

2.2 一致性研究工具

目前研究学业评价与课程标准的一致性工具，大致分为“韦伯分析模式”、“SEC分析模式”和“成功分析模式”，将三者进行比较，发现“成功分析模式”虽然比较精细化，但没有明确的临界水平，因此会对研究产生较大的个人主观性，在一定程度上会影响研究的信度，本文不采用此模式.进一步，“SEC分析模式”和“韦伯分析模式”是目前世界上研究一致性问题的主流工具，但是“SEC分析模式”虽然简单易于操作，但只分析两个维度，不如“韦伯分析模式”研究维度全面和深入.综上本文选择“韦伯分析模式”，并基于此模式进行适度本土化改造，以进行试卷与课程标准的一致性研究.

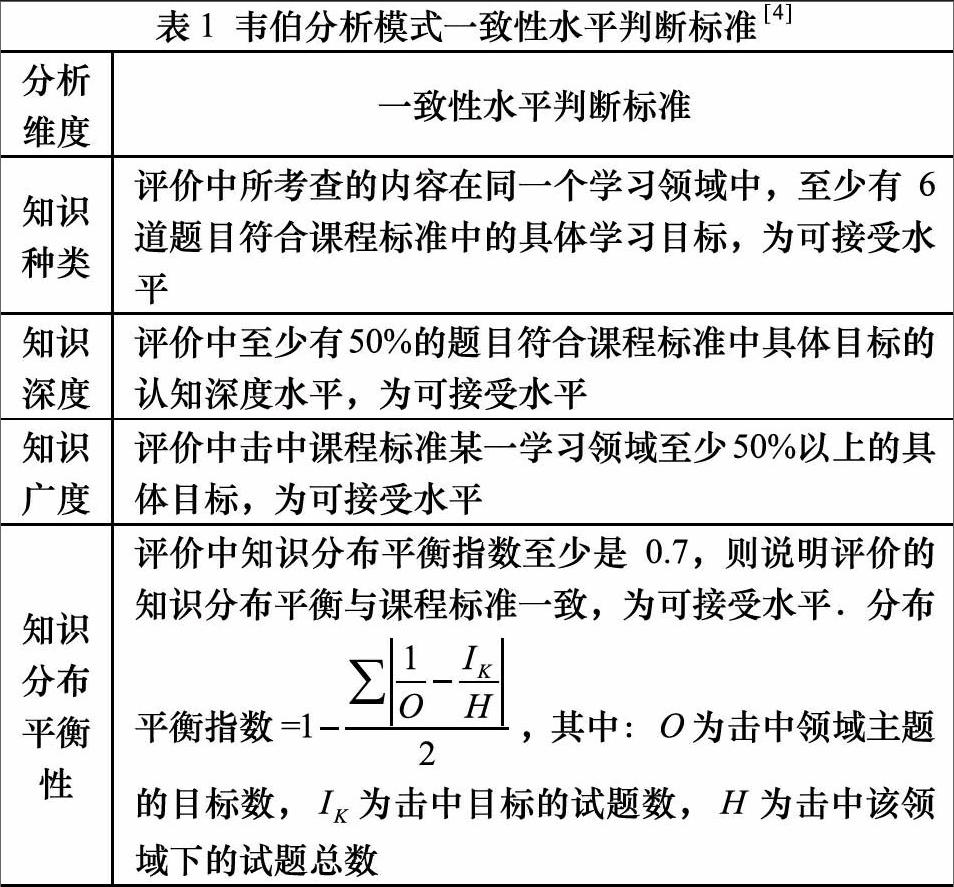
“韦伯分析模式”[3]主要是从知识技能和认知要求两个方面考量试卷与课程标准的一致性，又分为“知识种类”、“知识深度”、“知识广度”和“知识分布平衡性”四个维度，具体的一致性分析维度与可接受水平，

2.3研究过程

2.3.1对知识深度水平的编码

韦伯分析模式对知深深度水平划分，把试题和课程标准的认知水平分为4个等级：回忆、技能（概念）、策略性思维、拓展性思维，其主要是基于美国课程标准进行的认知水平划分，但由于课程标准制定受教育和经济发展水平等影响，具有一定的差异性.所以不能直接把它移植至我国课程标准进行水平编码，应对韦伯分析模式进行适度本土化改造，因此按照我国课程标准中对行为结果目标的认知水平，划分为相应的4个等级：“了解”、“理解”、“掌握”、“运用”，分别编码A，B，C，D.值得强调的是，课程标准中另一类是描述过程目标的行为动词，如“经历”、“体验”、“探索”等，这类过程目标在试卷中很难体现，当出现此类行为动词时，不进行具体目标水平划分，

2.3.2对数学课程标准内容的编码

（1）对课程标准内容的整体分析

课程标准对第三阶段（7-9年级）安排了4个模块的内容：“数与代数”、“图形与几何”、“统计与概率”、“综合与实践”，分为“数与式”、“方程与不等式”、“函数”、“图形的性质”、“图形的变换”、“图形与坐标”、“抽样与数据分析”、“事件的概率”、“综合与实践”等9个学习领域.每个学习领域又分为多个主题，例如“函数”领域下又分为“函数”、“一次函数”、“二次函数”、“反比例函数”这4个学习主题，需要说明的是，“统计与概率”模块直接分为“抽样与数据分析”、“事件的概率”两个学习主题，且内容不多，因此本文把它合并为“统计与概率”学习领域.此外，由于“综合与实践”模块是一类以问题为载体、以学生自主参与为主的学习活动[2]，设置目的在于培养学生综合运用有关的知识与方法解决实际问题，考查形式主要是以结果报告或者小论文进行评价，较不适宜卷面测验，所以编码时只对“数与代数”“图形与几何”“统计与概率”三大模块进行编码.

（2）对课程标准内容的具体编码原则

首先，对“数与代数”、“图形与几何”、“统计与概率”三大模块分别编码1、2、3，比如“图形与几何”我们编码为2，相应的领域“图形的性质”、“图形的变换”、“图形与坐标”分别编码2.1、2.2、2.3，对于“图形的性质”领域下的主题又分为“点、线、面、角”、“相交线与平行线”、“三角形”分别编码2.1.1、2.1.2、2.1.3…，，每个主题下又有若干具体目标，分别编码2.1、3.1、2.1_3.2、2.1.3.3……

其次，对课程标准内容中主题的具体目标进行编码，要按照不同的行为动词进一步拆分，例如“三角形”主题下的一条具体目标“理解三角形及其内角、外角、中线、高线、角平分线等概念，了解三角形的稳定性”，理解和了解是两个不同的行为动词，所以编码时把它拆为“2.1.3.1理解三角形及其内角、外角、中线、高线、角平分线等概念”和“2.1.3.2了解三角形的稳定性”.在所有具体目标编码完成之后，再根据相应的行为动词进行水平的划分.例如编码2.1.3.1中的行为动词与课程标准中的行为结果动词的“理解”相对应，于是编码2.1.3.1记为水平B，编码2.1.3.2记为水平A.对具体目标中仅有过程性目标，如仅出现“经历，体会，体验，探索”等行为动词时，不进行水平编码，也不统计具体目标总数，例如“体会抽样的必要性”；若具体目标中既有过程性目标又有结果性目标，则以结果性目标进行编码，如“探索并证明角平分线的性质定理”，按照结果性目标中的“证明”进行水平编码D.

（3） 2017年中考数学卷试题编码

对试题编码时，首先对试题的模块进行编码，之后对试题及其解答过程进行分解，梳理出本题考查的每一个知识点，知识点的个数记为测试题的个数，然后按照课程标准划分的具体目标进行编码，填到相应的试卷编码统计表中，例如，2017年福建省中考数学卷第11题填空题计算I一2 i -30，按照编码标准分析，本题涉及3个知识点，分别为有理数的绝对值、零指数幂、有理数的混合计算，对应的编码分别为1.1.1.5、1.1.1.8、1.1.4.1.endprint

3数据统计与分析

3.1总体一致性分析

2017年福建省中考数学卷与以往各设区市考查形式变化不大，过渡性较好，试题表现出“稳中有新、亮点鲜明”的特点，如第20题考查我国古代数学名题“鸡兔同笼”问题，第23题以热门的城市共享单车为背景考查统计知识，表明数学贴近生活又更好地为生活服务.全卷满分150分，总题量25题，有选择题、填空题、解答题三大题型，分别占10题共40分、6题共24分、9题共86分，按照对试题编码的原则对其进行模块分类，其中数与代数考查共59分，占39.3%；图形与几何共73分，占48.7%；统计与概率共18分，占12%.

在编码和统计后得到试卷与课程标准总体一致性结果如表3.在知识维度划分上，知识种类、知识深度、知识分布平衡性三个维度一致性较好，而知识广度一致性最差，具体原因在“知识广度”维度分析中有详细说明；在知识领域划分上，方程与不等式领域和课程标准吻合程度最好，其次是函数领域，而其他5个领域均有两个维度与课程标准表现出不一致，总之，2017年福建省中考数学试卷总体与课程标准表现出较好的一致性，但各维度、各领域一致性又有所差异.

3.2各维度一致性分析

（1）知识种类一致性分析

对试卷进行编码，得到7个领域与课程标准在知识种类维度的一致性统计表（表4）.可直观看出，在知识种类维度，数与式、方程与不等式、函数、图形的性质、图形的变化这5个领域均有不少于6道试题击中目标，表明这5个领域与课程标准具有一致性.但图形与坐标、统计与概率领域击中试题不足6道，说明这两个领域与课程标准不具备一致性，特别地，图形的性质领域击中目标数最多，为28个，这与图形的性质领域包含较多知识点有关，总体上，数与代数、图形与几何模块与课程标准在知识种类维度吻合程度较好，而统计与概率模块只击中5个目标，与课程标准不具备知识种类一致性，究其原因，可能是今年中考卷在这一模块未考查方差、平均数、随机事件等内容有关.

（2）知识深度一致性分析

在知识深度维度，试卷击中目标试题中至少有50%符合课程标准的知识深度水平，为可接受水平，从表5可知，今年中考试卷与课程标准保持高度一致性，仅有图形的变化领域不符合课程标准深度水平，进一步地，该领域有50%目标高于课程标准水平，导致这一现象的原因可能是，试卷把这部分内容放在解答题的最后几道考查，难度较大，以突显中考的选拔功能.

（3）知识广度一致性分析

对知识广度一致性分析时，首先对击中目标总试题数进行统计，对于击中重复的目标只保留一个，得到最终的具体目标总数.经过统计得到知识广度一致性表（表6），可见试卷与课程标准在知识广度上不具备一致性，但值得强调的是，由于考试形式与答题时间的限制，试卷对知识的考查不可能做到面面俱到，因此知识广度很难达到较高的百分比[5]，故国内大多数学者分析知识广度一致性时，认为知识广度百分比大于40%为勉强接受水平，进一步地，按照知识广度百分比大于40%为勉强接受水平，可知方程与不等式领域知识广度为勉强接受水平，而其他领域百分比在30%左右，均不足40%，因此试卷总体在知识广度维度一致性较差，

特别地，笔者在对课程标准编码过程中也发现，有些具体目标不适宜做卷面测试.例如，“会用计算器求平方根和立方根”、“能用计算器进行近似计算”，但现在中考已经明文规定不能使用计算器，所以这类目标就得不到考查；而有些具体目标则属于学习过程中的阶段性目标，但中考考查的知识较综合，例如，“能画出反比例函数的图像”、“会用描点法画出二次函数的图像”等，这或许也是导致知识广度一致性较差的原因.

（4）知识分布平衡性一致性分析

知识分布平衡性指的是击中目标在击中主题下的分布情况，如果试题击中某领域下的3个主题，且每个主题击中的目标试题数都是2，则分布平衡指数为1，说明知识分布最均匀.由表7可看出，中考试卷与课程标准在知识分布平衡性一致性较好，除“数与式”和“图形的性质”领域内的知识分布平衡指数稍低于0.7外，其他5个领域知识平衡一致性都为可接受，即在知识分布上是比较均匀的，不存在明显的领域知识分布缺失现象，需要指出的是，知识分布平衡指数受该领域击中目标试题数影响，击中试题越多平衡指数信度也就越高，研究也就更具有意义.

4研究结论及启示

（1）总体上，试卷与课程标准的一致性较好，在知识种类、知识深度、知识分布平衡性一致性较好，在知识广度一致性最差.在各维度中，知识种类能够涉及课程标准中的各个内容领域，但个别领域的击中题目量少于6道；在知识深度上，试题认知要求较符合课程标准的认知要求，个别高于课程标准要求，这可能与中考承载着选拔功能相关；在知识广度上，一致性较差，比率基本低于40%，不可接受，所以在保证考查核心内容的同时，试卷的知识广度需要提高；在知识分布平衡上，一致性较好，说明试卷在各个主题分布较为均匀.

（2）还需加强试题与课程标准的一致性.课程标准中的评价建议指出，对于学生基础知识和基本技能达成情况的评价，必须准确把握内容标准中的要求。例如，对于一元二次方程根与系数关系的考查，内容标准中的要求是“了解”，并不要求应用这个关系解决其他问题，设计测试题目时应符合这个要求.内容标准中的选学内容，不得列入考试范围.

（3）教学实践应以课程标准为依据.通过试卷考查的三大模块知识对比，图形与几何模块考查占据总分的半壁江山，而其他两大模块仅占一半，但人教版初中教材中“图形与几何”模块的总学时占40.3%，可见本套试卷考查偏向“图形与几何”模块，因此教学实践应以课程标准为依据，切实落实课标中的要求，谨防知识性的“偏科”，

此外，有些教师往往对中考试卷涉及的知识点着重讲解，而对于试卷中很少涉及的知识点仅做“了解”处理，但中考试卷受限于卷面和考试时间等因素，不能对所有知识点逐一考查，且中考试卷与课程标准的吻合程度并不完全一致.综上，以中考试卷考查的知识点作为教学的主要依据就有所欠缺.因此，教师课堂教学需以课程标准为准则，研读课标并正确地把握课标与考试和教学三者之间的关系，做到立足“双基”、渗透“数学思想”，帮助学生积累“活动经验”、“领悟”数学核心素养.

（4）课程标准中表现型评价的缺失，在一致性研究兴起的美国各州课程标准中，一般都包括学习内容标准和学生学习后的表现标准，然而，我国课程标准只规定了学习内容标准，存在对学生学习后的表现型评价的缺失，值得强调的是，我国课程标准还只是“看似一个缺少学习成果评价标准的课程内容框架”[6].虽然课程标准中有涉及到学业评价的宏观建议，但还是缺少对具体内容标准的表现型评价，因此建议课程标准修订组在后续课标修订中，适当加入表现型评价标准.

参考文献

[1]福建省人民政府办公厅，福建省“十三五”教育发展专项规划[S].福建省人民政府办公厅文件，2016

[2]中华人民共和国教育部.义务教育数学课程标准（2011版）[s].北京：人民教育出版社，2011

[3]Norman L. Webb. Alignment of science and mathematics standards[M] . National Institute for Science Education University ofWisconsin-Madison， 1999

[4]陈娴，郏璨璨，陈宁，物理内容标准与考试之间的一致性研究[J].课程·教材·教法，2010 （7）： 67-71

[5]金晓红，基于课程标准的浙江省高考数学试卷一致性分析[D].长春：东北师范大学，2012

[6]胡军学生学习成果评价标准不能在课程标准中缺失一澳大利亚科学课程内容与标準给我们的启示[J].课程教材教法，2005 （9）： 10-14endprint