关于处处可断图类的最大谱半径
武 建
(山西财经大学 应用数学学院, 山西 太原 030006)
0 引 言
图作为研究复杂网络的一种语言, 提供了用抽象的点和线表示各种实际网络的一种方法[1]. 在经济政治全球化背景下, 各个个体间既充满了竞争的必然性又涌现出合作的可能性, 现实中存在很多竞争与合作关系. 作为“竞争-合作”关系的一种模型, 假设存在11个竞争者, 且用字母A,B,C,D,E,F,G,H,I,J,K分别表示, 这里称每个字母为一个顶点. 若两个竞争者之间建立了直接且稳定的合作关系, 则认为这两个个体之间建立了关系. 此时, 在两个竞争个体对应的顶点间连一条线(称其为边), 来表示他们之间这种关系的存在; 否则, 两个顶点间不存在连线. 这11个个体之间的竞争与合作关系模型如图 1 所示. 该模型的一个显著特点是: 每个顶点均处在至少一个极小割集中.
设G是连通图, 若对于S⊂V(G),GS是不连通的(指GS至少包含两个连通分支), 则称S是G的一个割集. 若S是G的一个割集, 但S的任意真子集不是G的割集, 则称S是G的一个极小割集. 设h≥2的正整数,S⊂V是图G=(V,E)的极小割集. 若|S|≤h, 则称极小割集S是一个下h-割集. 若对任意的顶点v∈V(G)均存在一个下h-割集S使得v∈S成立, 则称图G是一个处处h-可断图. 所有具有n个顶点的处处h-可断图构成了一个新的图类, 即处处可断图类, 记作H(h,n). 对处处可断图类的研究在集成电路布线等问题中有实际意义. 关于处处可断图类的进一步研究见文献[2-6].
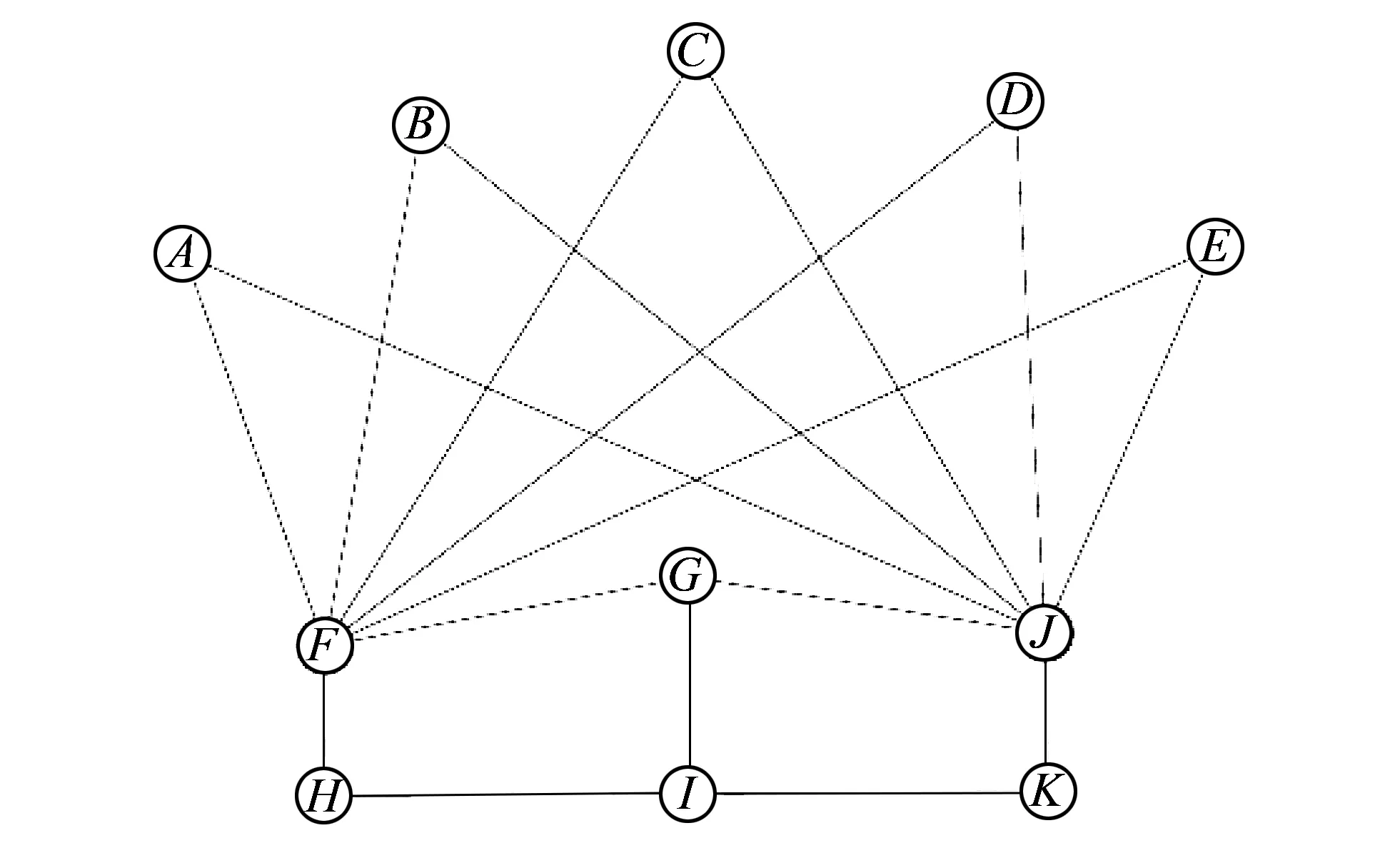
图 1 11个个体之间的竞争-合作关系模型Fig.1 Competition-cooperation model with 11 individuals
最小(边)割集覆盖问题是与处处可断图类研究相关的一类重要问题[7]. 处处可断图类的研究条件是每个顶点都处在至少一个极小顶点割集中. 从图的对偶性角度来看, 对该类图的研究有重要意义, 图谱理论是图论研究的重要领域之一. 本文讨论了处处可断图类的最大邻接谱半径问题, 并且构造了处处可断图类谱半径达到最大时的极图G*(见图 2). 同时, 给出了处处可断图类最大谱半径的一个确切的上界,
h=n-2, h≥3.
本文未提及术语参见文献[8].
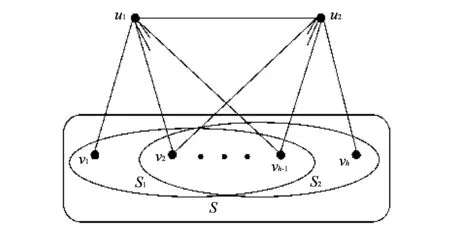
图 2 极图G*Fig.2 The extremal graph G*
1 预备知识
设A(G)是图G的邻接矩阵. 显然, 矩阵A(G)是实对称(0,1)矩阵, 其特征值均为实数. 图G的谱半径, 记作ρ, 是图G的邻接矩阵A(G)的最大特征根. 由Perron-Frobenius定理知, 谱半径是矩阵A(G)的单根, 且对应一个正的特征向量, 该向量被称为图G的Perron向量[9]. 本文依据图的顶点划分, 研究了处处可断图类的最大谱半径问题. 围绕Brualdi等[9]提出的关于确定给定图类谱半径上界的问题, 图的谱半径研究受到了广泛关注[10-12]. 文献[13-15] 对含有割边、 有割点的两类图的谱半径进行了研究. 关于图的谱半径研究的新热点见文献[16-17]. 文献[18-19]以病毒传播网络为研究背景, 研究了在给定图的直径下图的最大谱半径和最小谱半径.
对任意的图G, 本文用N(v)表示顶点v∈V(G)的邻集, 用G[A]表示由集合A⊂V(G)导出的子图. 图G的最大完全子图所包含的顶点数为图的最大团数, 记作ω(G)[20]. 设G∈H(h,n), 图G的可断数为
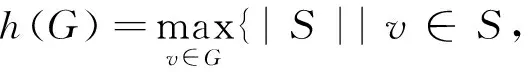
S⊂V(G)是图G的极小割集}.
通过参数h(G)和ω(G), 本文构造了处处可断图类谱半径达到最大时的极图G*(见图 2):
1) 顶点集V(G*)={u1,u2,v1,v2,…,vh};
2)S1={v1,v2,…,vh-1},S2={v2,v3,…,vh};
3)S=S1∪S2,S1∩S2={v2,v3,…,vh-1};
4)G*[S]导出顶点数为h的完全子图;
5)G*[S1],G*[S2]均导出顶点数为h-1的完全子图;
6)G*[S1∩S2]为顶点数至少为1的完全子图, 或空图;
7)N(u1){u2}=S1,N(u2){u1}=S2.
引理 1 任意一个非平凡且无环的连通图至少包含两个不为割点的顶点.
引理 2[4]S⊆V(G)是图G的极小割集的充要条件是对任意的顶点u∈S及连通分支G-S(记作G[A]或〈A〉), 有N(u)∩A≠φ成立.
引理 3 若图G∈H(h,n), 则: (1)2≤h≤n-2且n≥4; (2) 圈C4是最小的处处可断图.
证明 设G∈H(h,n), 则图G的阶数为n(>h). 若S⊂V(G)是图G的极小割集, 且|S|=h=n-1, 则G-S连通分支数为1. 这与S是图G的极小割集矛盾. 因此,h≤n-2成立. 若h<2, 则h=1. 于是, 图G的每个顶点均为割点. 这与引理1矛盾. 因而2≤h≤n-2, 且n≥4成立, 即结果(1)成立. 当n=4时, 即有结果(2)成立.
引理 4[4]若G∈H(h,n),v∈G是图G的割点, 则G-v的每个连通分支至少有4个顶点.
引理 5 若G∈H(h,n), 则图G的最小度δ满足δ≥2 .
证明 设G∈H(h,n), 顶点v∈G的度为1, 则其邻接顶点u必为割点. 于是, 必有G-u的一个连通分支只含有唯一的一个顶点v. 这与引理4矛盾.
由引理5可得如下结论.
推论 1 若G∈H(h,n), 则图G必定包含一个长至少为3的圈.
设顶点v∈G. 如果顶点v的邻集N(v)的导出子图是一个完全图, 那么称顶点v是图G的一个完全顶点. 下面的结论说明处处可断图不包含完全顶点.
引理 6[2]若G∈H(h,n), 图G不包含完全顶点.
2 主要结果及证明
2.1 主要结果
本节刻画了处处可断图类谱半径达到最大时的极图, 并计算了极图的谱半径.
定理 1 若图G∈H(h,n), 则当其谱半径达到最大时,G≅G*.
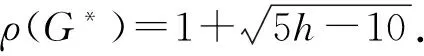
由定理 1 和定理 2 可得处处可断图类谱半径的上界.
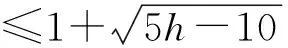
2.2 定理1的证明
设图G∈H(h,n), 由引理5知, 图G不包含1度顶点. 进而, 对任意的顶点v∈V(G), 其邻集必然满足|N(v)|≥2. 不失一般性, 设u1,u2是图G的两个顶点, 且边u1u2∈E(G). 为了方便刻画极图结构, 下面给出一些符号:N(u1),N(u2)分别表示顶点u1,u2的邻集;N(u1)∪N(u2),N(u1)∩N(u2) 分别表示集合N(u1),N(u2)的并和交;N(u1){u2},N(u2){u1},V(G){u1,u2},V(G)(N(u1)∪N(u2))均表示从点集中删除一个或一些点后得到的集合. 下面根据顶点u1,u2的邻集来划分图的顶点, 分两种情况, 利用若干命题完成定理的证明.
情况 1N(u1)∩N(u2)=φ.
命题 1 若N(u1)∩N(u2)=φ, 且有|N(u1){u2}|=|N(u2){u1}|=1成立, 则谱半径达到最大时,G≅G*.
证明 设N(u1){u2}={u},N(u2){u1}={v}.
1) 若V(G)(N(u1)∪N(u2))=φ, 图G≅C4. 否则, 图G不是处处可断图.
2) 若V(G)(N(u1)∪N(u2))≠φ, 则|V(G)(N(u1)∪N(u2))|≥1. 因为在连通图上添加边可以使图的谱半径增大[21], 所以当谱半径达到最大时, 图G的结构可由下面步骤得到: Step1.添加边使得集合V(G){u1,u2}在新图中导出一个完全子图Kn-2; Step2.将顶点u1连接到集合V(Kn-2){v}的每个顶点; Step3. 将顶点u2连接到集合V(Kn-2){u}的每个顶点. 由构造可知, 当谱半径达到最大时,G≅G*. 命题得证.
运用与命题1类似的证明过程(2)可得如下结论.
命题 2 若N(u1)∩N(u2)=φ, 且有|N(u1){u2}|=1, |N(u2){u1}|≥成立, 则谱半径达到最大时,G≅G*.
命题 3 若N(u1)∩N(u2)=φ, 且有|N(u2){u1}|=1, |N(u1){u2}|≥2成立, 则谱半径达到最大时,G≅G*.
命题 4 若N(u1)∩N(u2)=φ, 且有|N(u1){u2}|≥2, |N(u2){u1}|≥2成立, 则谱半径达到最大时,G≅G*.
情况 2N(u1)∩N(u2)≠φ.
命题 5 若N(u1)∩N(u2)≠φ, 且有|N(u1)∩N(u2)|=1,V(G)(N(u1)∪N(u2)≠φ成立, 则谱半径达到最大时,G≅G*.
证明 假设符号:N(u1)∩N(u2)={w},N1=N(u1){u2,w},N2=N(u2)(u1,w}. 因为V(G)(N(u1)∪N(u2))≠φ, 所以|V(G)(N(u1)∪N(u2))|≥1成立. 由图G的结构知, 顶点ui(i=1,2)与V(G)(N(u1)∪N(u2))中的点均不相邻.
若|Ni|=0(i=1,2), 则ui(i=1,2)构成图G的一个完全顶点. 这与引理6矛盾. 所以, 必有|Ni|≥1(i=1,2)成立. 设w1∈N1,w2∈N2, 则当谱半径达到最大时, 图G的结构如下: Step1.添加边使得集合V(G){u1,u2}在新图中导出一个完全子图Kn-2; Step2.将顶点u1连接到集合V(G)(N(u1)∪N(u2))包含的每个顶点; Step3.将顶点u1连接到集合N2{w2}包含的顶点; Step4.将顶点u2连接到集合V(G)(N(u1)∪N(u2))包含的每个顶点; Step5. 将顶点u2连接到集合N1{w1}包含的顶点. 特别地, 若Ni{wi}=φ(i=1,2)时, 则不添加边. 由构造可知, 当谱半径达到最大时,G≅G*. 命题得证.
命题 6 若N(u1)∩N(u2)≠φ, 且有|N(u1)∩N(u2)|=1,V(G)(N(u1)∪N(u2))=φ成立, 则谱半径达到最大时,G≅G*.
证明 假设符号:N(u1)∩N(u2)={w},N1=N(u1){u2,w},N2=N(u2){u1,w}, 则必有|Ni|≥1(i=1,2)成立. (如若不然, 假设|N1|=0. 因为V(G)(N(u1)∪N(u2))=φ, 且顶点u1与集合N2中的顶点均不相邻, 所以G[N(u1)]在图G中导出一个完全子图. 这与引理6矛盾. )
设w1∈N1,w2∈N2, 则当谱半径达到最大时图G结构如下: Step1. 添加边使得集合V(G){u1,u2}在新图中导出一个完全子图Kn-2, 这里V(G){u1,u2}=N1∪N2∪{w}; Step2. 将顶点u1与集合N2{w2}包含的每个顶点连接, 特别地, 若N2{w2}=φ则不添加任何边; Step3. 将顶点u2与集合N1{w1}包含的每个顶点连接, 特别地, 若N1{w1}=φ则不添加任何边; 可以验证,G≅G*. 命题得证.
下面考虑当N(u1)∩N(u2)={p1,p2,…,pm}(m=2,3,…)的情形. 假设N1=N(u1){u2,p1,p2,…,pm},N2=N(u2){u1,p1,p2,…,pm}.
命题 7 若N(u1)∩N(u2)≠φ, 且有|N(u1)∩N(u2)|=m(m=2,3,…),V(G)(N(u1)∪N(u2))≠φ成立, 则谱半径达到最大时,G≅G*.
证明 设v∈V(G)(N(u1)∪N(u2)), 则必有u1与N2中的点不相邻;u2与N1中的点不相邻;v与顶点ui(i=1,2)不相邻; |N1∪N2|=0或|N1∪N2|≥1成立.
1) 当|N1∪N2|=0时, 若G[{p1,p2,…,pm}]导出完全子图, 则图G包含完全顶点, 与引理6矛盾. 因此, {p1,p2,…,pm}中必然包含两个不相邻顶点. 不妨设p1p2∉E(G). 于是, 当谱半径达到最大时图G的结构可由如下步骤得到: Step1.添加边使得V(G){u1,p1}在新图中导出一个完全子图Kn-2; Step2.将顶点u1与集合V(Kn-2){v}中的每个顶点连接; Step3.将顶点p1与集合V(Kn-2){p2}中的每个顶点连接. 可以验证,G≅G*.
2) 当|N1∪N2|≥1时, 不妨设u∈N2. 当谱半径达到最大时图G的结构可由如下步骤得到: Step1.添加边使得V(G){u1,p1}在新图中导出一个完全子图Kn-2; Step2.将顶点u1与集合V(Kn-2){u}中的每个顶点连接; Step3.将顶点u2与集合V(Kn-2){v}中的每个顶点连接. 可以验证,G≅G*. 由1), 2)知, 命题得证.
命题 8 若N(u1)∩N(u2)≠φ, 且有|N(u1)∩N(u2)|=m(m=2,3,…),V(G)(N(u1)∪N(u2))=φ, |N1∪N2|≥1成立, 则谱半径达到最大时,G≅G*.
证明 下面分1)|Ni|=0, |Nj|≥1,i=1,2, 且i≠j; 2)|Nk|≥1,k=1,2, 两种情形完成证明.
若1)成立, 设|N1|=0, |N2|≥1, 且v∈N2, 则根据引理6, {p1,p2,…,pm}中必然包含两个不相邻顶点. 不妨设p1p2∉E(G). 当谱半径达到最大时图G的结构可由如下步骤得到: Step1.添加边使得v(G){u1,p1}在新图中导出一个完全子图Kn-2; Step2.将顶点u1与集合V(Kn-2){v}中的每个顶点连接; Step3.将顶点p1与集合V(Kn-2){p2}中的每个顶点连接. 可以验证,G≅G*.
若2)成立, 不妨设q1∈N1,q2∈N2, 则当谱半径达到最大时图G的结构可由如下步骤得到: Step1.添加边使得V(G){u1,u2}在新图中导出一个完全子图Kn-2; Step2.将顶点u1与集合N2{q2}中的每个顶点连接; Step3.将顶点u2与集合N1{q1}中的每个顶点连接. 可以验证,G≅G*. 通过对1), 2)的分析, 命题得证.
命题 9 若N(u1)∩N(u2)≠φ, 且有|N(u1)∩N(u2)|=m(m=2,3,…),V(G)(N(u1)∪N(u2))=φ, |N1∪N2|=0成立, 则谱半径达到最大时,G≅G*.


由于G′ ≅G, 因而当谱半径达到最大时,G′与G对应的极图相同. 当谱半径达到最大时, 图G对应的极图G*可由如下方法得到:

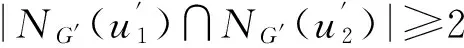
由情形1和情形2可得, 当其谱半径达到最大时,G≅G*.
2.3 定理2的证明
设图G*的顶点集为V(G*)={u1,u2,v1,v2,…,vh}, 图G*的一个Perron向量为X=(xu1,xu2,xv1,…,xvh}, 其中, 分量xui与ui(i=1,2)对应; 分量xvj与顶点vj(j=1,2,…,h)对应. 因为顶点vj1,vj2(j1,j2∈{2,3,…,h-1})有相同的邻集, 所以xvj1=xvj2成立. 简记xv2与顶点集{v2,v3,…,vh-1}中的每个顶点对应. 由于A(G*)X=ρX, 所以如下方程成立,
ρxu1=xu2+xv1+(h-2)xv2,
ρxu2=xu1+xvh+(h-2)xv2,
ρxv1=xu1+xvh+(h-2)xv2,
ρxvh=xu2+xv1+(h-2)xv2,
ρxv2=xu1+xu2+xv1+xvh+(h-3)xv2.
因为图G*包含圈, 所以图G*的谱半径ρ>2[9]. 解以上方程构成的方程组可得
xu1=xu2=xv1=xvh,
ρxu1=2xu1+(h-2)xv2,
ρxv2=4xu1+(h-3)xv2.
进一步求解得
ρ2-2ρ-5h+11=0,
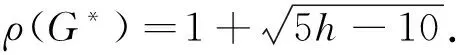
命题得证.
3 结 论
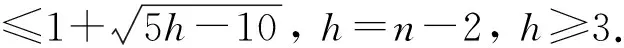
任意一个图均可看作某个处处可断图的子图. 在理论上, 可用处处可断图来估计其它图的谱半径的界和其它参数的界. 作为一种解决问题的方法, 结果具有重要的理论意义. 没有建立有效的算法来构造处处可断图类, 并深入讨论该图类的代数结构是结果的不足之处, 也是有待改进的方面.
[1]汪小帆, 李翔, 陈关荣. 网络科学导论[M]. 北京: 高等教育版社, 2013.
[2]贾晓峰, 朱必文. 一类图中的最大团[J]. 系统科学与数学, 1988, 8(3): 226-233. Jia Xiaofeng, Zhu Biwen. The maximum clique in an everywhere separable graph[J]. Journal of System Science and Mathematical Science Chinese Series, 1988, 8(3): 226-233. (in Chinese)
[3]武建, 贾晓峰, 孙立新. 一类图的可加边问题[J]. 太原科技大学学报, 2006, 27(6): 495-500. Wu Jian, Jia Xiaofeng, Sun Lixin. The additive edge prpblem in separable graph[J]. Journal of Taiyuan University of Science and Tehcnology, 2006, 27(6): 495-500. (in Chinese)
[4]Jia X F. Some results concerning the ends of minimal cuts of simple graphs[J]. Discussiones Mathematicae, 2000, 20(1): 139-142.
[5]武建. 处处可断图的若干问题研究[D]. 太原: 太原理工大学, 2007.
[6]马红平. 关于连通图断片的一些结果[J]. 徐州师范大学学报 (自然科学版), 2005, 23(2): 19-21. Ma Hongping.Some results of about the ends of connected graphs[J]. Journal of Xuzhou Normal University (Natural Science Edition), 2005, 23(2): 19-21. (in Chinese)
[7]Hoshino E A. The minimum cut cover problem[J]. Electronic Notes in Discrete Mathematics, 2011, 37: 255-260.
[8]Bondy J A, Murty U S R. Graph theory with applications[M]. London: Macmillan, 1976.
[9]Bruadli R A, Solheid E S. On the spectral radius of complementary acyclic matrices of zeros and ones[J]. SIAM Journal on Algebra Discrete Methods, 1986, 7(2): 265-272.
[10]李乔, 冯克勤. 论图的最大特征根[J]. 应用数学学报, 1979, 2(2): 167-175. Li Qiao, Feng Keqin. On the largest eigenvalue of graphs[J]. Acta Mathematicae Applicatae Sinica, 1979, 2(2): 167-175. (in Chinese)
[11]Cvetkovi D, Simi S. Graph spectra in computer science[J]. Linear Algebra and Its Applications, 2011, 434(6): 1545-1562.
[12]Hansen P, Stevanovi D. On bags and bugs[J]. Discrete Applied Mathematics, 2008, 156(7): 986-997.
[13]Liu H Q, Lu M, Tian F. On the spectral radius of graphs with cut edges[J]. Linear Algebra and Its Applications, 2004, 389(1): 139-145.
[14]Berman A, Zhang X D. On the spectral radius of graphs with cut vertices[J]. Journal of Combinatorial Theory Series B, 2001, 83(2): 233-240.
[15]武建. 一类图的谱半径[J]. 太原理工大学学报, 2010, 41(3): 320-322. Wu Jian. The spectral radius on a class of graphs[J]. Journal of Taiyuan University of Technology, 2010, 41(3): 320-322. (in Chinese)
[16]Tian X G, Wang L G, Lu Y. On the second smallest and the largest normalized Laplacian eigenvalues of a graph[EB/OL]. [2017-06-10]. http:∥120.52.73.76/arxiv.org/pdf/1603.04301.pdf.
[17]Lin H Y, Zhou B. Distance spectral radius of uniform hypergraphs[EB/OL]. [2017-06-09]. http:∥120.52.73.78/arxiv.org/pdf/1602.08214.pdf.
[18]Van Dam E R. Graphs with given diameter maximizing the spectral radius[J]. Linear Algebra and Its Applications, 2007, 426(2/3): 454-457.
[19]Van Dam E R, Kooij R E. The minimal spectral radius of graphs with a given diameter[J]. Linear Algebra and Its Applications, 2007, 423(2/3): 408-419.
[20]Yuan X Y, Shao J Y, Liu Y. The minimal spectral radius of graphs of order n with diameter n-4[J]. Linear Algebra and Its Applications, 2008, 428(11/12): 2840-2851.
[21]Cvetkovi D M, Doob M, Sachs H. Spectra of graphs[M]. Third Ed. Heidelberg-Leipzig: Johann Abrosius Barth Verlag, 1995.

