高频隔离型准Z源逆变器的建模与分析

李 山 ，司文旭 ，陈 艳 ，崔 森

（1.重庆理工大学电气与电子工程学院,重庆400054；2.重庆市能源互联网工程技术研究中心,重庆400054）

随着全球能源的危机，特别是不可再生资源的持续降低，各个国家都先后步入新能源的研究行列。在过去的研究当中，分布式发电占据很大一部分比例。由于这些分布式发电，易受环境变化的影响，使其输出的电压波动比较大。因此需要一些特殊的逆变器进行稳压稳频，进而供给广大用户使用。传统的电压源逆变器和电流源逆变器由于采用两级变换结构，增加其控制的复杂程度，同时降低系统的整个效率。为此研究者先后提出不同的新型逆变器。其中，Z源/准Z源逆变器是目前研究较多的一类逆变器，该类逆变器不但可以实现升降压的目的，而且还使原来的两级结构降低一级结构，既提升系统效率，又降低控制复杂程度。因此，这类逆变器得到了广泛的使用与研究。

为了研究ZSI/QZSI源逆变器拓扑特性，设计ZSI/QZSI源逆变器控制器。文献[1]对模型进行动态建模和分析；文献[2]提出ZSI/QZSI光伏并网系统的电容电压恒压控制策略，实现了ZSI/QZSI光伏并网系统的闭环控制和最大功率点跟踪，同时可确保在同等输出输入电压比的情况下开关器件电压应力最小；文献[3]对ZSI/QZSI的升压控制策略进行研究；文献[4]提出新的DC/DC升压变换器拓扑用于分布式发电系统，该拓扑包含电压反馈、单相隔离、倍压整流变压器，增加了转换器的功率密度；文献[5]提出了输入串联输出并联隔离DC/DC转换器的QZSI；文献[6-8]通过改进主电路阻抗网络结构来提高升压因子，使得在不改变直通占空比的情况下可以得到更高的升压因子；文献[8-9]提出改变电路结构以求减小支撑电容电压等级等。这些文献都在一定程度上改善了ZSI/QZSI所存在的电流出现断续，开关器件电压应力大、开机输入电流冲击大的问题，但其缺乏电气隔离的特性。

针对系统的建模，文献[10]提出基于最小二乘系统辨识算法的逆变器模型；文献[11]提出了基于Wiener模型的非线性系统辨识技术的逆变器建模；文献[12]根据广义状态空间平均法建立其数学模型；文献[13]提出根据信号流程，推导准Z源逆变器的交流小信号模型等。基于以上建模方法，并比较分析，本文采用物理意义清晰，所得到模型的形式十分简洁，便于控制系统传递函数计算的状态空间平均法建立其数学模型。

1 高频隔离型准Z源逆变器

由于Z源逆变器和准Z源逆变器缺乏电气隔离特性，在准Z源逆变器的基础上提出了高频隔离型的准Z源逆变器。如图1所示为高频隔离型准Z源逆变器的拓扑结构。

图1 高频隔离型准Z源逆变器的拓扑结构Fig.1 High frequency isolation quasi-Z source inverter topology

该逆变器结构，通过增加高频变压器构成输入输出隔离型电路，同时在控制策略中实现前后级的耦合统一。增加了电气隔离特性，能够凭借变压器的变比得到更高的升压因子，使得该电路实际应用更加广泛。

2 原理分析

对于传统电压型或电流型逆变器，逆变桥上下桥臂的导通是绝对禁止的，因为这会导致短路并毁坏变换器。由文献[13-14]可知，在准Z源逆变器中，上下桥臂直通状态是允许的，该状态中电感充电，电压升高。在非直通状态中，电感放电，能量通过变压器传输到副边。直通工作状态的时间可以是部分或者全部的逆变器传统零矢量时间，也就是嵌入到逆变器的续流状态中，不会影响逆变器输出电压的变化。因此高频隔离型准Z源逆变器也存在直通和非直通两种工作状态。

由文献[15]知，当Z网络电感的电感过小则会出现电流断续的情况，所以本文假设电感比较大，使电路工作在电流连续的状态，对其电路进行稳态分析。

假设变压器为理想变压器且变比为N，即变压器Vs=NVp，其中，Vp、Vs分别为变压器一、二次侧电压。根据变压器内部磁通平衡可知，如果变压器原副边电流之和能够保证磁通平衡，就能够保证电流的连续性。由于变压器本身更相当于是一个储能电感，与非隔离准Z源逆变器中的电感效果相同[15-17]。同时，由图1中电感与电容的串联结构可以看出，副边绕组与电容的组合其实是将原边绕组与电容组合扩展延伸而已，在电压上进行N倍作用，在电流1/N上进行操作。所以可以将副边元件折算到原边进行等效，此时原边电容电压需要以副边电容电压VCs/N替代。在直通状态工作下，其等效电路模型如图2所示。

图2 直通状态下等效电路模型Fig.2 Equivalent circuit model in shoot-through state

由图2可得

在非直通状态工作下，其等效电路模型如图3所示。由图可得

图3 导通状态下等效电路模型Fig.3 Equivalent circuit model in nonshoot-through state

假设在一个周期内直通占空比为D，则非直通占空比为1-D，根据电感的伏秒特性，整个开关周期内平均电压等于0，可得

根据单相逆变器输出电压，推导可得输出交流电压的峰值为

式中，M为逆变器调制度。因此，可得单相逆变器的输入、输出电压传递增益G为

从式（8）中可以看出，由于逆变器调制度M≤1，而D＜0.5，且变压器变比N≥1（一般变比N给定），因此通过改变M与D实现输入输出升降压控制。

3 基于状态空间平均法的建模

本文采用最常用的状态空间平均法对电路进行小信号建模。等效电路模型[17]如图4所示。图中，V和R分别为电感与电容的等效电阻。

图4 等效电路模型Fig.4 Equivalent circuit model

在直通工作状态时，电路中开关管S导通，二极管断开，电路处于储能状态。此时原边电感充电，电容放电，副边电容充电，变压器放电。取状态变量为L1、L2、VCS、VC2；输入变量为VS、Idc，输出量为Vdc，则在直通工作电路状态下的方程为

在非直通工作状态，此时电路中开关管S断开，二极管导通，电路处于能量传输状态。此时原边电感放电，电容充电，副边电容放电，变压器传输能量到负载端，逆变侧可以简化等效为恒流源，电流为idc，电压为vdc。取相同的状态变量，则在非直通工作状态下的方程为

则可得系统的平均状态方程为

当系统处于稳态时

不考虑电感、电容的串联等效电阻时，可得

解方程可得

由式（18）可见，其推导结果与上文稳态情况下的推导结果一致。在状态变量和控制变量的稳态值中加入小信号扰动量，然后进行拉普拉斯变换，进而可以推导出系统的小信号模型。以作为扰动变量加入到原来的稳态变量，X和U分别为x和u的稳态值，再忽略小信号的二次项，可得

为了简化建模过程，假设C1=C2=CCs=C，L1=L2= L，对式（19）的两边进行拉普拉斯变换，整理得

可见，阻抗网络2个电感电流的稳态值相同，但小信号扰动值不一定相同，从而显示出二者的动态响应不一定相同，同时也说明，推导的小信号模型对研究其动态过程很有必要。

整理式（20），可得直通占空比到副边电容电压的传递函数为

可推导出直通占空比到副边电容电压的传递函数为

由式（22）可以看出，在系统右平面存在零点。根据控制原理可知，对于任何系统，凡是右平面存在零点的系统都是不稳定的。在阶跃输入下，系统初始输出都会存在一个向下的负脉冲。

4 模型参数分析

由上述分析可得，该传递函数在s平面的右半部分存在零点，该点随着电感、电容和控制量的改变而变化。系统的振荡和非最小相位现象同时也会随着这些值的变化而变化。以单一某参数的变化对系统的影响为例进行说明。系统参数如表1所示。

（1）改变电感的数值，取L=200～1 000 μH，系统变化结果如图5所示。由图5可知，当电感从200 μH到800 μH变化时，左半平面的极点和右半平面零点沿实轴方向随电感的增大而靠近原点；右半平面零点越靠近原点，系统的负冲就越严重；随着极点向原点移动，系统的过渡过程时间也会增大，振荡频率减小。

表1 系统参数Tab.1 System parameters

图5 电感变化时系统的零点极点Fig.5 Zero-pole point map of the system when inductance changes

（2）改变电容的数值，取C=220～1 000 μF，系统变化结果如图6所示。由图6可见，虽然零点的位置不发生变化，但是极点随着电容的增大而向原点移动，同时也会增大上升时间和减小振荡频率。这些极点、零点轨迹清楚地说明虽然大的电感和电容有利于减小稳态电压纹波和电流纹波，但是会使暂态响应变坏。因此在实际应用中选择具体的参数还需兼顾系统的稳态、暂态性能。

（3）改变直通占空比的数值，取D=0.15～0.28，其结果如图7所示。

直通占空比决定着直流链电压升压比，是逆变器的一个重要的控制参数。由图7可以发现，极点的位置随着D的增大而向实轴移动，这会减小系统的振荡频率；但是右半平面零点也向原点移动，这预示了会加剧非最小相位的负冲。

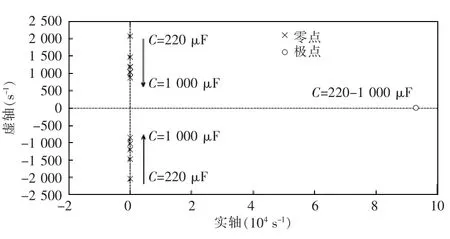
图6 电容变化时系统的零点极点Fig.6 Zero-pole point map of the system when capacitance changes

由前文推导知，VCs=（1-D）Vdc，可得

进而可得直通占空比到直流侧电压的传递函数

由此可以看出，直通占空比对逆变器直流侧电压Vdc的传递函数有2个零点，这2个零点的位置同样会随着电感、电容参数值的变化而变化，即当Z源网络参数值变大时，右半平面的零点就靠近虚轴，非最小相位现象变得严重，当Z源网络参数值变小时，右半平面的零点就远离虚轴，非最小相位现象减轻。非最小相位现象的存在使得Z网络电容电压在输入电压出现扰动时，输出会出现超调和振荡，特别是出现大扰动时，非最小相位对系统的影响更加明显。而在Z源逆变器中Z网络参数变化范围不会很大，因此仅通过调整Z源网络参数的方法来减小非最小相位现象是不容易实现的。

5 模型仿真

在Saber软件中搭建功率主电路，如图8所示；在MATLAB/Simulink中建立小信号模型进行仿真[18，19]。

以变压器二次侧电容电压VC1s的输出响应为例，当两者的输入相同时，其小信号模型仿真结果如图9所示；其实际电路仿真结果如图10所示。对比分析可以发现，小信号模型的电压输出波形与实际电路模型的电压输出波形基本一致，进而证明了所建小信号模型的正确性。

进一步对实际电路进行仿真，其中输入侧电源为稳定的直流电压源。根据前文各参数在模型中输出特性，各参数值选取如表2所示。

图8 高频隔离型准Z源仿真电路Fig.8 Simulation circuit of high-frequency isolated quasi-Z-source

图9 小信号模型输出的Vc1s波形Fig.9 Waveform of Vc1soutput by small signal model

图10 实际电路模型输出的Vc1s波形Fig.10 Waveform of Vc1soutput by the actual circuit model

表2 系统仿真参数Tab.2 System simulation parameters

本文采用的调制方法为简单的升压调制法。其实现过程就是将直通状态包含于逆变器传统零矢量状态之内，Z源拓扑族逆变器的一种简单的调制策略，控制策略信号波形如图11所示。控制逆变桥的SPWM波由两个反相的正弦波与三角波交截产生。直通状态由直流电压Vp、Vn与相同三角波交截得到。其中Vp与Vn大小相等方向相反，进而可以得到恒定的直通占空比D，且此时的直通量由于插入在传统零矢量中，因此直通工作过程对逆变级的调制不产生影响。

按上述参数仿真的结果如图12所示。由图12可以看出，VC1=168.56 V，VC2=49.312 V，VCls=336.14 V，Vdc=437.2 V。将该输入值代入上述推导公式中求取理论推导结果，可得：VC1=169 V，VC2=49 V，VCls= 338 V。由此可以看出，理论值与仿真值基本完全吻合，验证理论与分析正确性。

图11 控制策略信号波形Fig.11 Signal waveforms under the control strategy

图12 电路仿真波形Fig.12 Waveforms in circuit simulation

增大Z网络中电感参数值的仿真波形如图13所示。由图13可知，当增大Z网络中电感的参数值时，系统出现振荡，达到稳定的时间变长。验证了随着电感参数值的增大，系统的过渡过程时间延长的特性。

图14是变压器副边电容电压与直流侧电压的仿真波形。由仿真结果可得，其满足说明理论与分析的正确性。

本仿真结构采取的变压器是2倍关系，即输出侧电压是输入侧电压的2倍，其仿真结果如图15所示，可以看出：VS=2VP。

输出电压有效值如图16所示，由图可得其有效值为219.91 V。由上述公式推导：Vn=314 V，vn= 222 V。仿真结果与理论值基本相符。

图13 增大Z网络中电感参数的仿真波形Fig.13 Simulation waveforms when increasing Z network inductance

图14 Vcs与Vdc仿真波形Fig.14 Simulation wareforms of Vcsand Vdc

图15 变压器仿真波形Fig.15 Simulation wareforms of transformer

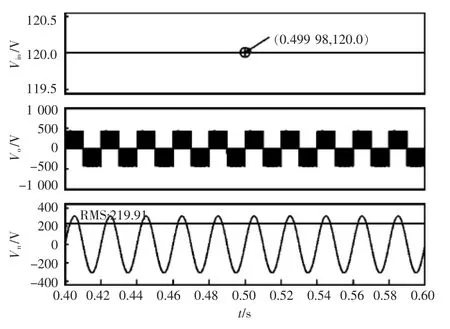
图16 输出电压仿真波形Fig.16 Simulation wareforms of output voltage

将高频隔离型准Z源逆变器与Z源和准Z源逆变器在相同输入情况下进行比较分析，结果如表3所示。

由表3可得，在相同的输入下，高频隔离型准Z源逆变器由于加入变压器变比使得逆变器输出较高的电压。即在相同输出情况下，高频隔离型准Z源逆变器需要的输入值较小，这使高频离型准Z源逆变器的电容电压应力相对于Z源逆变器和准Z源逆变器的较小，避免了开关器件电压应力大、开机输入电流冲击大的问题，同时还可以降低整个逆变器系统的体积。另外由于高频离型准Z源逆变器引入了变压器使得输入和输出之间产生了电气隔离，并能够凭借变压器的变比得到更高的升压因子，进一步降低输出侧电压和电容电压应力。

表3 系统输出结果Tab.3 Results of system output V

6 结语

本文是对提出的高频隔离型准Z源逆变器拓扑结构的建模与分析。首先对高频隔离型准Z源逆变器的基本工作原理进行研究，在此基础上进行小信号建模，并对结果进行了归纳描述；再根据所建模型对高频隔离型准Z源网络中各个参数特性进行分析，得出各参数在变化时对系统动态性能的影响；根据参数特性，选取合适的参数值在Saber软件中建立电路进行仿真，仿真结果与理论推导基本一致，证明理论分析和模型建立的正确性。最后对相关Z源逆变器进行比较，比较结果表明在相同的输出情况下，高频隔离型准Z源逆变器的输入电压较低，电容电压应力较低，减小器件损耗，提高整体电路效率同时还实现了电气隔离的特性，这在逆变器的运用方面，特别是新能源（如太阳能，风能等）发电方面有很高的研究价值。

[1]Liu Jingbo,Hu Jiangang,Hu Longya.Dynamic modeling and analysis of Z source converter derivation of AC small signal model and design oriented analysis[J].IEEE Transactions on Power Electronics,2007,22（5）：1786-1786.

[2]李媛,彭方正.Z源/准Z源逆变器在光伏并网系统中的电容电压恒压控制策略[J].电工技术报,2011,26（5）：63-69.

Li Yuan,Peng Fangzheng.Constant capacitor voltage control strategy for Z-Source/Quasi-Z-Source inverter in gridconnected photovoltaic systems[J].Transactions of China Electrotechnical Society,2011,26（5）：63-69.

[3]李斌,刘洁,吴菲,等.准Z源逆变器升压控制策略研究[J].电子世界,2012（10）：92-93.

Li Bin,Liu Jie,Wu Fei,et al.Research on boost control strategy for quasi-Z-source inverter[J].The electronic world. 2012（10）：92-93.

[4]Vinnikov D,Roasto I.Quasi-Z-source-based isolated DC/DC converters for distributed power generation[J].IEEE Transactions on Industrial Electronics,2011,58（1）：192-201．

[5]Martinez C,Jalakas T,Vinikov D,et al.QZSI DC/DC converters in input-series output-parallel connection for distributed generation[J].International Symposium on Power Electronics, Electrical Drivers,Automation and Motion,2012：952-957.

[6]Loh P C,Gao Feng,Blaabjerg F.Embedded EZ-source inverters[C].IEEE Transcations on Industry Applications,2010,46（1）：256-267．

[7]Gao Feng,Loh P C,Li D,et al.Asymmetrical and symmetrical embedded Z-source inverters[C].IET Power Electronics,2011,4（2）：181-193．

[8]Li Ding,Loh P C,Zhu Miao,et a1.Cascaded trans-Z-source inverters[C].IEEE Transactions on Power Electronics,2011,1976-1980.

[9]Qian Wei,Peng Fangzheng,Cha Honnyong.Trans-Z-source inverters[C].IEEE Transactions on Power Electronics,2010, 26（12）：3453-3463．

[10]熊小伏,陈康,郑伟,等.基于最小二乘法的光伏逆变器模型辨识[J].电力系统保护与控制,2012,40（22）：52-57.

Xiong Xiaofu,Chen Kang,Zheng Wei,et al.Photovoltaic invertermodelidentification based on leastsquares method[J].Power System Protection and Control,2012,40（22）：52-57.

[11]郑伟,熊小伏.基于Wiener模型的光伏并网逆变器模型辨识方法[J].中国电机工程学报,2013,33（36）：18-26.

Zheng Wei,Xiong Xiaofu.A model identification method for photovoltaic grid-connected inverters based on the Wiener model[J].Proceedings of the CSEE,2013,33（36）：18-26.

[12]方宇,谢勇.电子镇流器中谐振逆变器建模方法研究[J].电力电子技术,2006,40（5）：98-100.

Fang Yu,Xie Yong.Modeling method for resonant inverter applied to electronic ballast[J].Power Electronics,2006,40（5）：98-100.

[13]蔡春伟,曲延滨,盛况.准Z源逆变器的暂态建模与分析[J].电机与控制学报,2011,15（10）：7-13.

Cai Chunwei,Qu Yanbin,Sheng Kuang.Transient modeling and analysis of quasi-z-sources-inverter[J].Electric Machines and Control.2011,15（10）：7-13.

[14]Li Yuan,Anderson J,Peng Fangzheng,et al.Quasi Z source inverter for photovoltaic power generation systems [C].IEEE Applied Power Electronics Conference&Exposition,2009：918-924.

[15]丁永欢.高频隔离准Z源逆变器的研究与应用[D].南京：南京理工大学,2013.

Ding Yong huan.Research on high frequency isolated Quasi-Z-source inverter and application[D].NanJing.Nanjing University of Science&Technology.2013.

[16]Ding Yonghuan,Li Lei,Liu Jiaojiao.High frequency transformer isolated cascaded Quasi-Z-Source inverter[C].Industrial Electronics&Applications,2012：792-796.

[17]Ding Yonghuan,Li Lei.Research and application of high frequency isolated Quasi-Z-Source inverter[J].Conference of the IEEE Industrial Electronics Society,2012：714-718.

[18]邵桂荣,苏世栋,詹平红.DC-DC开关变换器的动力学建模与稳定性分析[J].重庆理工大学学报：自然科学版, 2010,24（11）：93-96.

Shao Guirong,Su Shidong,Zhan Pinghong.Dynamic modeling and stability studyof DC-DC switching converter[J]. Journal of Chongqing University of Technology：Natural Science,2010,24（11）：93-96（in Chinese）.

[19]王博,陈万强,李祥阳.电液舵机系统的建模及模型验证研究[J].重庆理工大学学报：自然科学版,2015,29（12）：133-137.

Wang Bo,Chen Wanqiang,Li Xiangyang.Modeling and electro-hydraulic steering system model validation studies [J].Journal of Chongqing University of Technology：Natural Science,2015,29（12）：133-137（in Chinese）.