同心圆拟合法在海洋钢结构测量中的应用

，，，， ，，

(海洋石油工程股份有限公司，天津 300452)

海洋钢结构大部分都由圆钢管组成。圆管端部圆心坐标精度至关重要，是控制海洋钢结构精度的重要环节，其中的导管架顶部导管跨距、井口导向管空间位置等关键位置关系到海上安装能否顺利进行。因此，精确测量并计算这些关键位置的管端坐标非常必要。文献[1-2]只测量圆周外侧若干点，点数少而且只分布在圆周一侧上，计算圆心精度较低，文献[3-6]采用带理论约束半径的算法，提高了部分圆管圆心精度，但是，由于圆管在加工制造过程中，存在一定的圆度误差及半径误差，导致圆管的真实半径和理论半径并不一样，因此带理论约束半径的算法并不是最精确的方法。运用自由设站法可以测量整个圆周上的测量点，但是自由设站过程比较耗时，效率低下，而且在转站过程中还存在公共标靶坐标的匹配误差[7-8]，也不是最好的方法。

基于上述问题，本文提出一种新方法——三维空间圆管端部同心圆拟合法，该方法可使测量点数增加一倍，测量范围扩大一倍，如图1所示，采用全站仪无棱镜模式首先测量圆管端面上的若干点，再测量圆管端面附近的内皮和外皮若干点，运用坐标转换法和最小二乘法拟合同心圆圆心坐标。该方法较传统方法的圆心计算精度大幅提高，对于海洋钢结构圆管端部的准确控制具有重要作用。

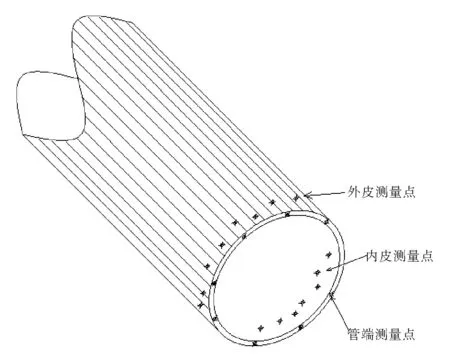
图1 测量点在圆管上分布示意图Fig.1 Survey points distribution on the circular tube

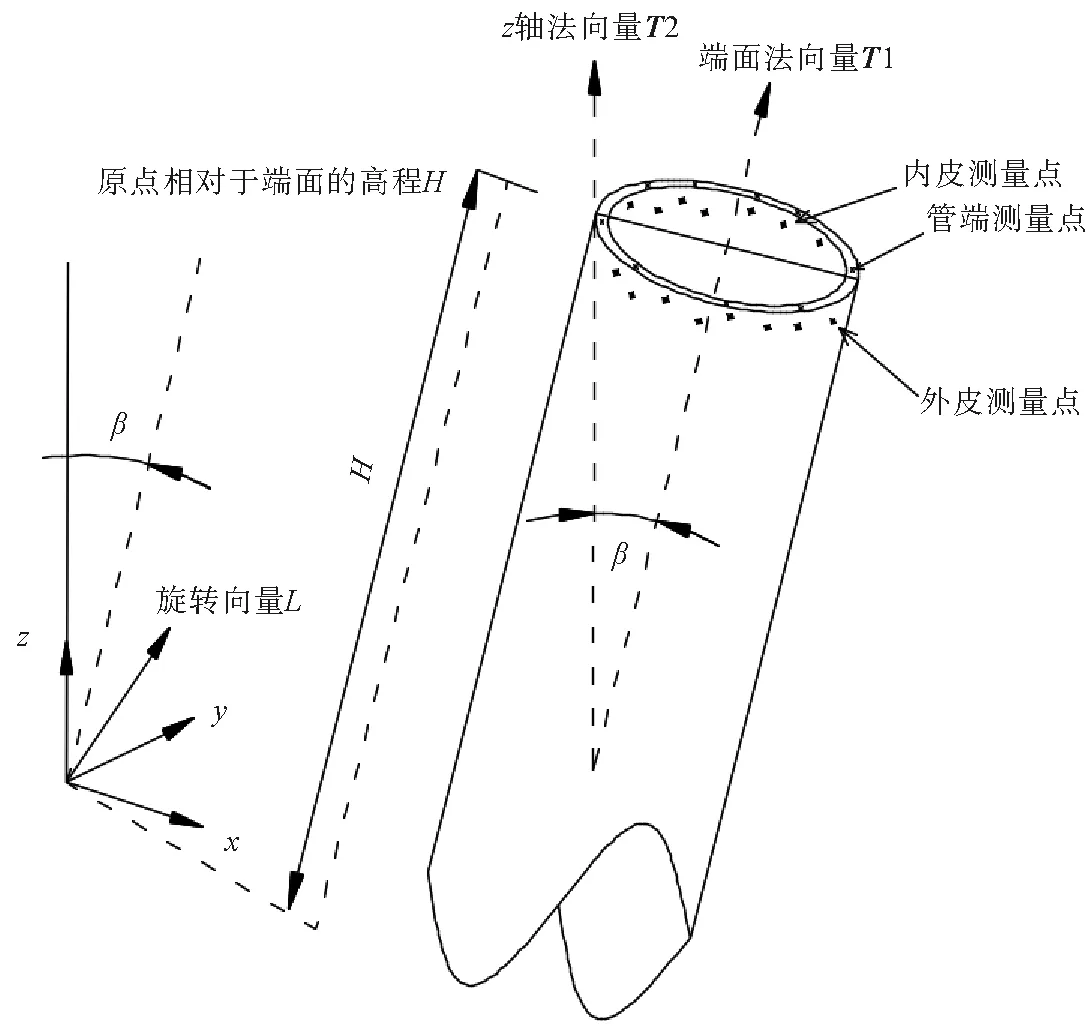
图2 圆管测量点坐标变换示意图Fig.2 Survey points coordinates alternation

1 测量点坐标转换过程

全站仪测量圆管端面上一些点的三维坐标(多余3个点以上)以及端面附近内皮、外皮若干点的三维坐标。外皮上测量点坐标为(x1i、y1i、z1i),(i=1,2,…,m)(m>3)，内皮测量点坐标为(x2i、y2i、z2i),(i=1,2,……n)，如图2所示。

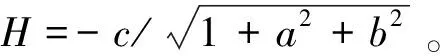
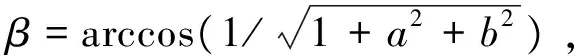
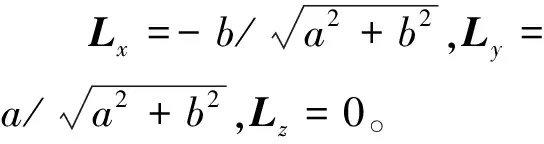
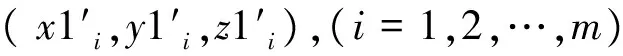
至此，坐标转换后的测量点在xy平面内分布形状为一组同心圆离散点，如图3所示。

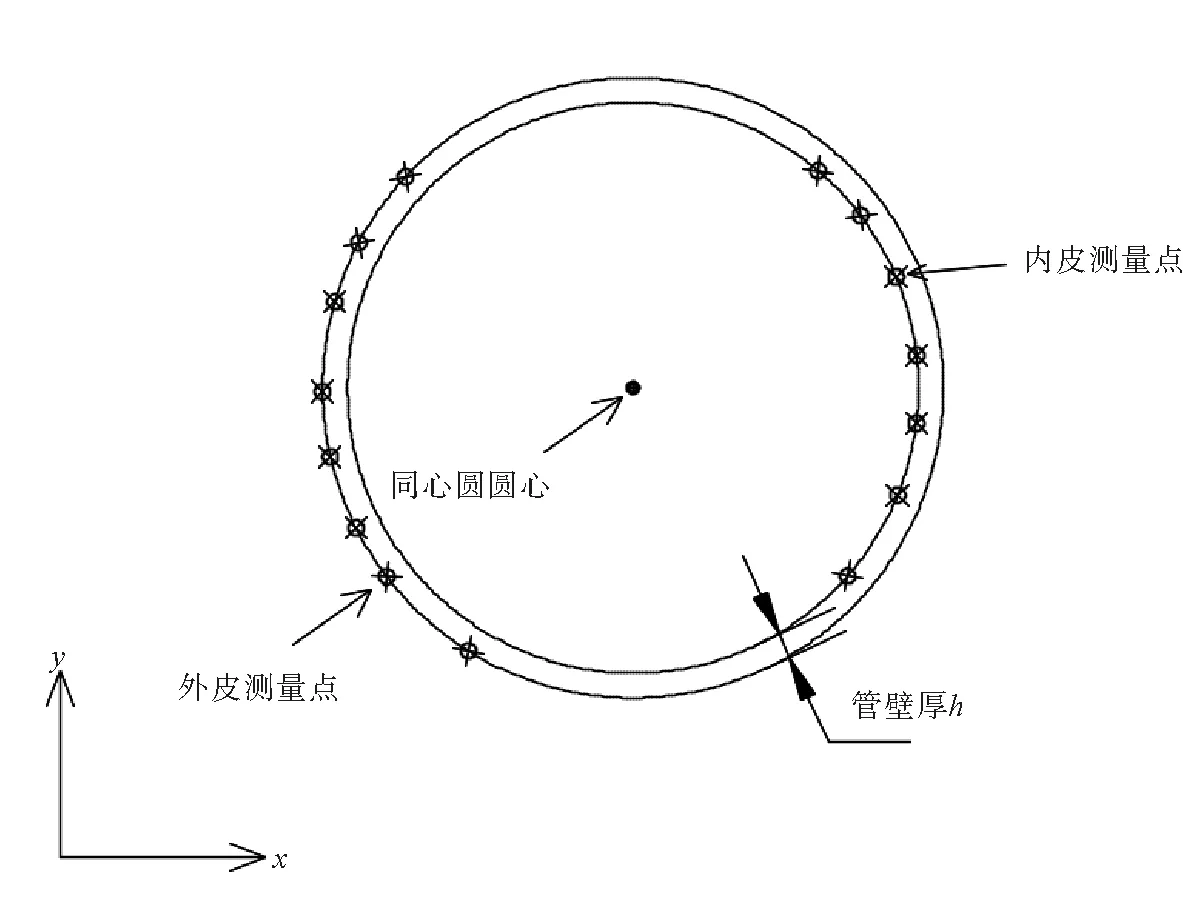
图3 测量点坐标变换后在XY平面内形成同心圆分布图Fig.3 Survey points in XY plane after coordinates alternation

2 同心圆拟合数学计算

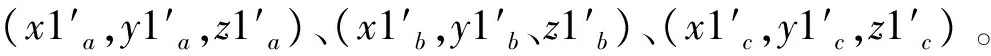
为计算参数初始值，由外设圆方程x2+y2+Dx+Ey+F=0,通过三点平面坐标可以计算参数D、E和F, 由此可知：p0=-0.5D,q0=-0.5E,

圆管的厚度已知为h，设同心圆的圆心坐标为(p,q)，外圆半径为r，可知：

外圆方程为：

(x1′-p)2+(y1′-q)2=r2；

(1)

内圆方程为：

(x2′-p)2+(y2′-q)2=(r-h)2。

(2)

将式(1)与式(2)方程用泰勒公式展开得误差方程：

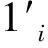
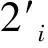
平差方程的矩阵形式函数模型为

令

根据间接平差原理[13-16]，可知

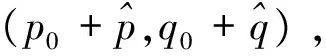
3 实验数据及分析

现场测量渤中34-9项目WHPB导管架预制导管端面及内外皮上若干数据三维坐标，已知导管理论外半径为1 185 mm，理论内半径1 105 mm，管厚度为80 mm。测量数据如表1所示。

分别运用本文同心圆拟合方法、单独外皮数据拟合方法、单独内皮数据拟合方法、单独外皮数据加约束半径拟合方法、单独内皮数据加约束半径拟合方法，计算圆管端部圆心坐标，计算结果如表2所示。

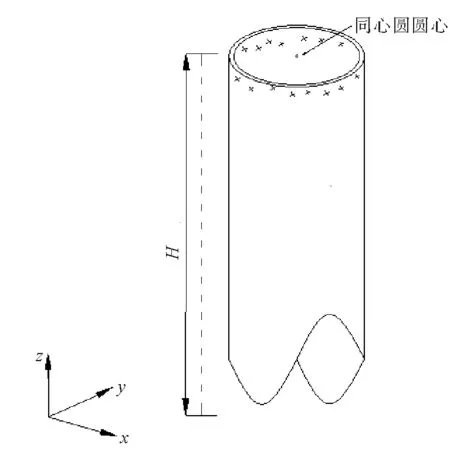
图4 坐标变换后的同心圆圆心三维坐标Fig.4 3 D coordinate of circle center after coordinates alternation

由表2 可以看出，由于同心圆拟合法测量的点数更多，且较均匀地分布在内外圆周上，计算圆心的点位中误差最小，计算的内外半径比较贴近理论半径，精度最高。单独计算内外皮数据法的圆心点位中误差最大，计算的半径偏离真实半径较大，精度最低[11-12]。加理论约束半径法计算的圆心点位中误差较小[3-6]，但由于圆管加工制造存在误差，其真实的半径与理论半径并不相等，用理论半径作为约束条件也存在一定的误差。因为同心圆拟合法比其他方法测量的数据更多，精度更高是必然的，为了证明测量相同点数情况下其精度更高，现同心圆拟合法的数据采用外皮的P1、P3、P5、P7、P9点与内皮的P10、P12、P14、P16点，这样测量点数与其他方法相同，计算结果见表2最后一行。结果显示其计算的半径与圆心点位中误差较其他方法更合理。说明除了测量点数量外，测量点的分布范围也是影响圆心精度的重要因素，分布范围越大，计算精度越高。各算法的圆心分布俯视图如图5所示,可以看出同心圆算法的圆心位置大致在中间位置。

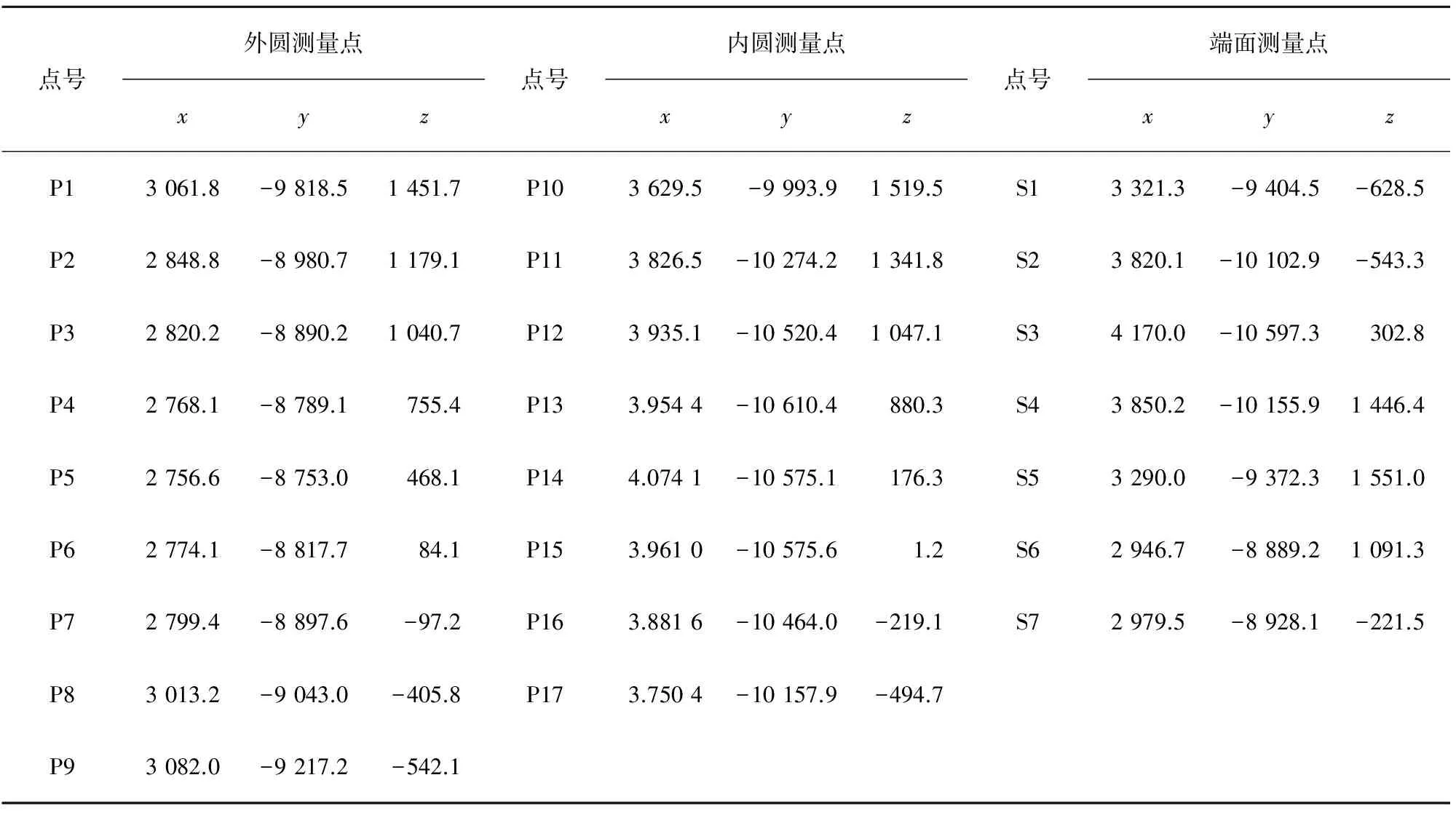
表1 测量点数据表Tab.1 Survey points data mm

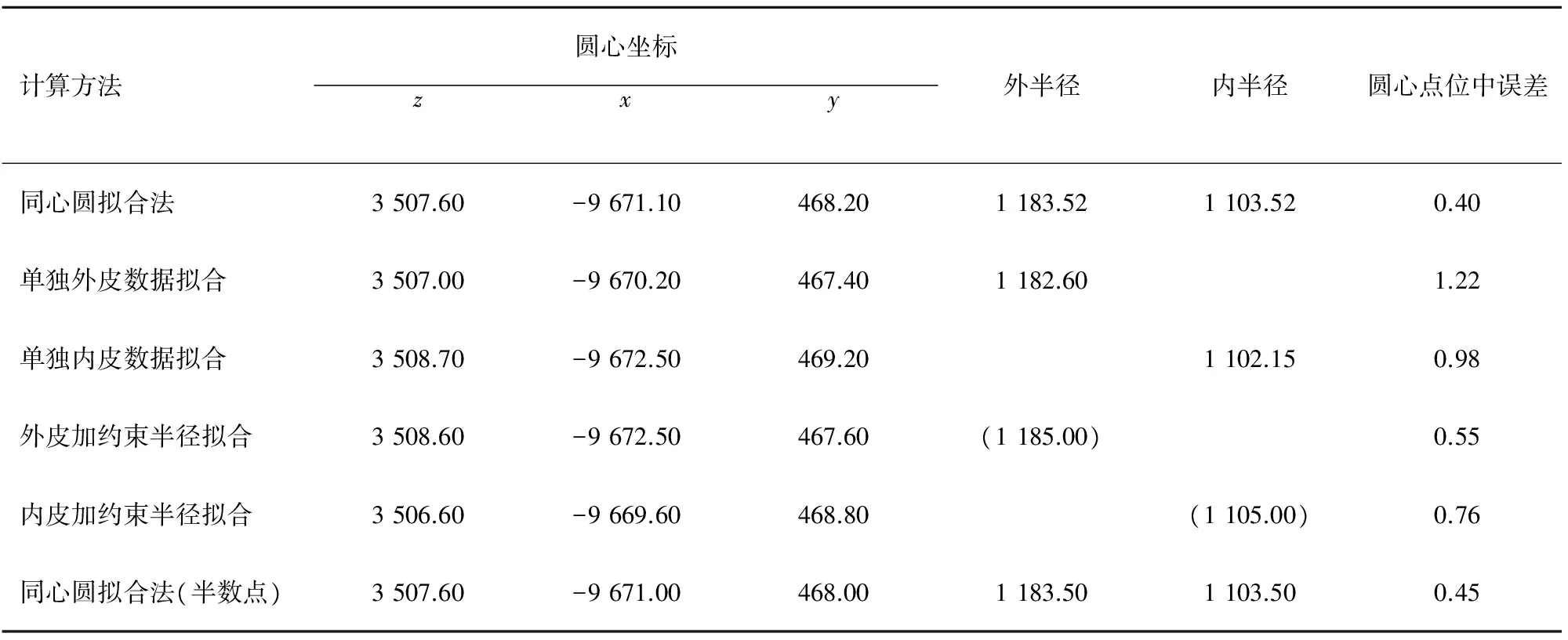
表2 几种方法计算的数据结果Tab.2 Result of various calculating methods mm

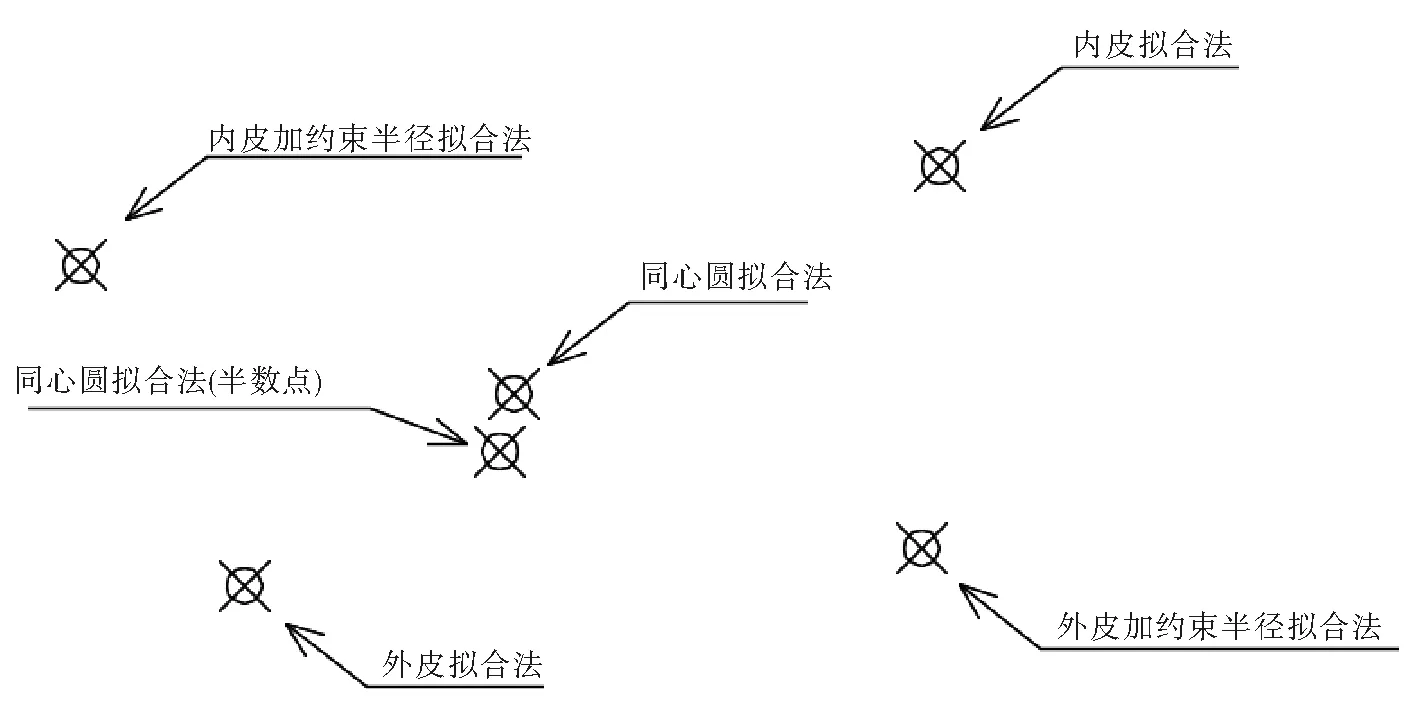
图5 各算法圆心分布示意图Fig.5 Circle center position of various methods

4 结论

通过数据实验分析可知，同心圆拟合法得到的圆管端部圆心的计算精度高于其他方法，因为计算中既增加了测量点数量，又扩大了测量点的分布范围。因全站仪一站就可以同时测量圆管内外皮，较自由设站法测量整个圆周的效率更高，且避免了自由设站公共标靶的匹配误差问题。算法中加入了坐标转换过程，可以实现对任意倾度圆管端部圆心的计算。

[1]张士舰,刘春杰,肖立权,等. 一种导管架钢桩跨距精确测量的新方法[J].中国海上油气,2014,26(5):92-95.

ZHANG Shijian,LIU Chunjie,XIAO Liquan,et al. A new method for accurate measurement of spans among jacket piles[J]. China Offshore Oil and Gas,2014,26(5):92-95.

[2]FITZGIBBON A,PILU M,FISHER R B. Direct least square fitting of ellipses[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1999,21(5):476-480.

[3]刘元朋,张定华,桂元坤,等. 用带约束的最小二乘法约束平面圆曲线[J].计算机辅助设计与图形学学报,2004,16(10):1382-1385.

LIU Yuanpeng,ZHANG Dinghua,GUI Yuankun,et al. Fitting planar circles with constrained least squares[J]. Journal of Computer Aided Design and Computer Graphics,2004,16(10):1382-1385.

[4]朱嘉,李醒飞,谭文斌,等. 基于圆心约束最小二乘圆拟合的短圆弧测量[J].光学精密工程,2009,17(10):2486-2492.

ZHU Jia,LI Xingfei,TAN Wenbin,et al. Measurement of short arc based on center constraint least-square circle fitting[J].Optic and Precision Engineering,2009,17(10):2486-2492.

[5]刘珂,周富强,张广军. 半径约束最小二乘圆拟合方法及其误差分析[J].光电子·激光,2006,17(5):604-607.

LIU Ke,ZHOU Fuqing,ZHANG Guangjun. Radius constraint least square circle fitting method and error analysis[J]. Journal of Optoelectronics·Laser,2006,17(5):604-607.

[6]刘春杰,张士舰,李小红,等. 一种导管架整体尺寸的检测方法[J].测绘工程,2014,23(2):39-44.

LIU Chunjie,ZHANG Shijian,LI Xiaohong,et al. A method of surveying Jacket’s whole dimensions[J].Engineering of Surveying and Mapping,2014,23(2):39-44.

[7]刘春杰,张士舰,孙云虎. 三维坐标系下检测导管架圆形杆件空间位置状态的方法：ZL201010115279X[P].2012-11-28.

[8]李继忠.野外自由设站的粗差探讨[J].科技情报开发与经济,2003,13(4):137-138.

LI Jizhong. Discussion on the gross errors of field free stations[J]. Journal of Library and Information Science,2003,13(4):137-138.

[9]王洪.全站仪自由设站法精度分析及应用研究[J].测绘与空间地理信息,2016,39(4):82-85.

WANG Hong. Free station’s accuracy analysis and research of its application[J]. Geomatics and Spatial Information Technology,2016,39(4):82-85.

[10]张士舰,刘春杰,李金富,等. 投影圆度判别法的圆柱拟合[J].测绘科学技术学报,2014,31(4):355-358.

ZHANG Shijian,LIU Chunjie,LI Jinfu,et al. Cylinder fitting with roundness estimate method[J]. Journal of Geomatics Science and Technology,2014,31(4):355-358.

[11]蒲竞秋.短圆弧测试方法与误差分析[J].机械,2002,29(增):35-36.

PU Jingqiu. Short arc measure method and error analysis[J]. Mechanical,2002,29(S):35-36.

[12]杜存飞,王康为.大半径小圆弧测量方法及误差分析[J].科技信息,2008,22(5):18-19.

DU Cunfei,WANG Kangwei.Measurement of large radius small arc and error analysis[J]. Science and Technology Information,2008,22(5):18-19.

[13]武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M].武汉:武汉大学出版社,2003:102-148.

[14]王解先,季凯敏.工业测量拟合[M].北京:测绘出版社,2008:51-52.

[15]樊功瑜. 误差理论与测量平差[M].上海:同济大学出版社,1998:97-132.

[16]靳祥生.测量平差[M].郑州:黄河水利出版社,2010:88-110: