基于加性分解的轧机液压伺服位置系统控制

吕书豪，张 磊

（河北工业大学控制科学与工程学院，天津 300131）

0 引 言

液压伺服位置系统是各种现代机械的重要组成部分，由于其质量比高，响应速度快[1]。常用于各种自动化制造系统，如轧机的辊缝控制、航空航天飞行控制执行器、汽车主动悬架以及各种广泛自动化制造系统[2]。

液压伺服系统的主要部件是泵、蓄能器、安全阀、伺服阀和液压执行器。蓄能器和安全阀分别增加和除去压力管路中的流体，以保持供应系统的压力。伺服阀通过输入电气信号控制液压执行器的压力和运动，液压执行器驱动负载，到达所需的位移、速度或负载的压力。然而，固有的非线性特性[3]逐渐限制了系统性能的提升。

另外，建模不确定性[4]，包括参数不确定性和不确定性非线性（未建模的非线性，如外部干扰、泄漏和摩擦等）可能导致控制精度差甚至不稳定[5-6]。

为提高具有非线性和不确定性液压伺服系统的性能，已有研究提出先进的非线性控制器，如基于误差的自适应符号积分鲁棒控制[7]、自适应鲁棒控制[8]、自适应反步控制[9]、反馈线性化控制[10]、基于扰动观测器的控制[11]等。这些非线性控制器在不确定的非线性液压系统中解决了控制问题，且得到了实测验证。与传统的线性控制器相比，尽管这些控制技术在提高控制性能方面是有效的，但都在不同程度上依赖被控对象或事先需要明确不确定性和扰动。

通常，由于难以直接测量摩擦和负载的干扰，因此需要采用自适应或估计算法来估计干扰。前人的研究[12]中通常使用了包含噪音测量信号的导数，系统可能不稳定。

本文从工程角度出发，设计了一种基于ASD方法的控制器，该控制器简单可靠，能够保证轧机液压伺服位置跟踪系统最终有界稳定且具有良好的鲁棒性和平稳的控制输入。最后通过仿真验证了该控制器能够满足控制要求。

1 液压伺服位置系统模型描述

所研究的液压伺服系统的控制方案如图1所示。图中xd为位置期望值，xp为位置反馈值。

液压缸力平衡方程[13]可以表示为

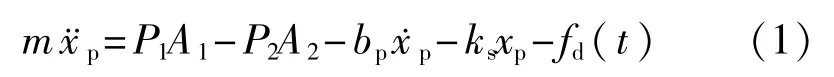
式中：m——上辊运动部件和柱塞的等效总质量；

xp——负载的位移量（增/减对应于轧机辊缝的减/增）；

P1、P2——液压缸两腔的压力；

A1、A2——两腔的有效面积；

bp——粘性摩擦系数；

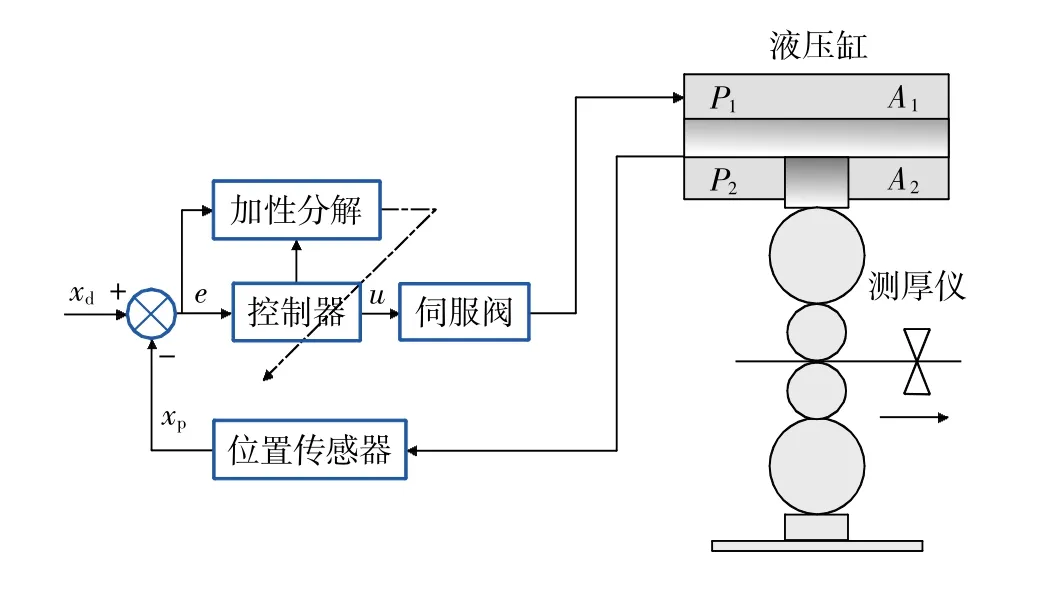
图1 轧机液压伺服位置控制方案

ks——负载弹性刚性系数；

fd（t）——作用在柱塞上的外负载力。

其中P1和P2可以表示为

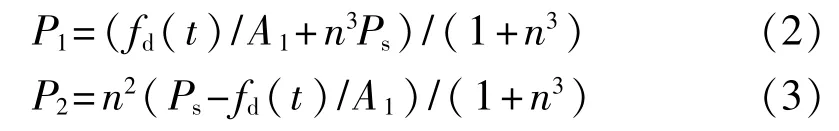
式中液压缸两腔有效面积比n=A2/A1，Ps是供油压力。

不考虑外部泄漏，执行器的流量方程[14]可以表示为

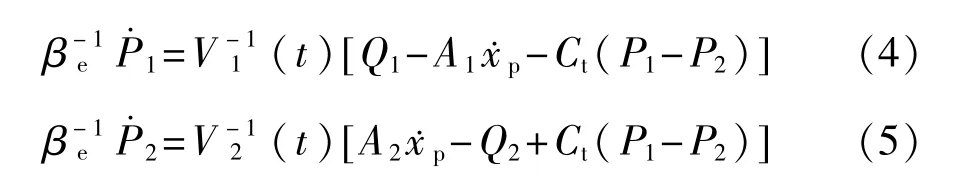
式中：V1（t）=V10+A1xp——活塞无杆腔的总控制体积；

V2（t）=V20-A2xp——活塞有杆腔的总控制体积；

V10、V20——两腔的初始控制体积；

βe——有效弹性模量；

Q1、Q2——流入无杆腔和流出有杆腔的流量；

Ct——执行器的内部泄露系数。

Cd、w——伺服阀流量系数和面积梯度；

ρ——液压油密度；

xv——阀芯位移；

Pr——回油压力。

考虑到研究中使用的伺服阀的响应特性比执行器的运行频带高得多，伺服阀的线性模型可以表示为

式中：kxv——伺服阀增益；

u——控制输出。

结合式（6）、式（7），可以得到：

对于系统模型（11），针对具有各种建模，参数不确定性和未知外部扰动的情况下，目标是使用合适的控制器输出u使惯性负载位置xp能够跟踪特定的运行轨迹。

2 控制器设计

2.1 问题描述

轧机液压伺服系统模型改写成误差模型。首先假定位置期望值xd有界，并且存在且有界。

通过引用文献[16]，式（12）中的e˙可以使用如下形式表示：

假设式（13）可控，则矩阵 K∈R3×1总是可以满足A+BKT是稳定的。则：

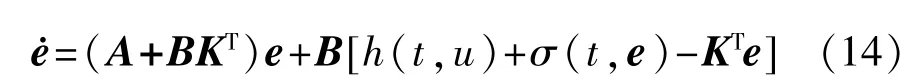
本文的控制目标是设计一个稳定的控制器u使系统状态趋于一个很小的值，或者在时变扰动情况下，当t→∞ 时，e→0。

2.2 ASD动态逆设计

ASD原理是将一个非线性系统分解为两个子系统：1）线性时不变的主系统，包含所有期望和扰动信号；2）不包含期望和扰动信号的次系统[17]。通过ASD，液压伺服系统首先转换为一个不确定自由的系统，但是扰动都集中在输出上，然后针对这个转换的系统应用动态逆方法；分析最终闭环系统的性能。

2.2.1 定义输出矩阵

基于矩阵 A+BKT，重新定义输出矩阵C∈R3×1。

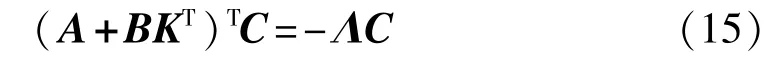
式中 Λ=diag（λ1，λ2，λ3），其中λ1，λ2，λ3为（A+BKT）T的特征值。

定义新的输出y=CTe，则其导数可以表示为

新的输出矩阵C使得从u到y的单入单出系统变为最小相位系统。因此，有y→0就有e→0，那么就有动态逆控制y→0。

2.2.2 加性状态分解

现在考虑系统（16）为原始系统。主系统选为

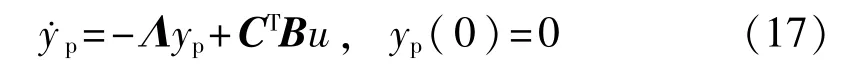
定义一个次系统输出ys可以表示为

从原始系统和主系统推导出次系统为

定义传函：

式中I1为单位矩阵。

重新整理式（16）～式（19）可得：

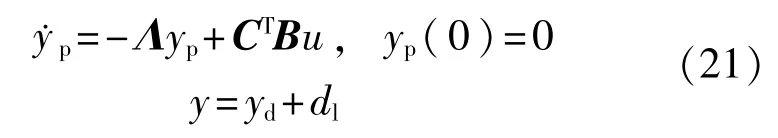
其中dl的拉普拉斯转换为

这是集中扰动，es是次系统的状态。

式（21）可以以传函形式重写为

dl集中扰动包括不确定性、扰动和输入。由于上式中y和yp（s）=G（s）u（s）已知，那么集中扰动可以表示为

通过ASD控制，目标转换为：针对式（22）设计一个有界控制器u使得输出y最终在很小的一个范围内，或者在时变不确定下，当t→∞就有y（t）→0。

2.2.3 动态逆控制

通过ASD，不确定系统（13）首先转为不确定自由系统（22），针对系统（22），因为G是最小相位和已知的，动态逆追踪控制器设计表述如下：

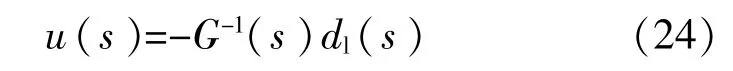
但控制器（24）因为分子的阶数比分母的阶数高，所以不能实现。在这里引入低通滤波矩阵Q（s）=1/（εs+1），其中ε＞0可以看做一个奇摄动参数。 控制器（24）变为

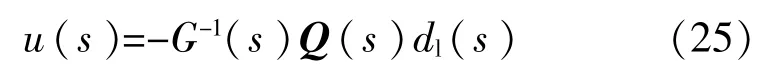
将式（23）代入式（25），即可得到 PI形式控制器：

式中 CTe作为输入，只要det（CTB）≠0，那么此控制器就可实现。至此完成了基于ASD方法的控制器设计。

3 系统仿真

为了验证所给出方案的有效性，本文采用Matlab对系统进行仿真，以某1450mm四辊可逆轧机为例。仿真中的主要物理参数如表1所示。

假设油缸期望位置xd=1 cm，初始条件为e（0）=[0.01 0 0]，fd（t）表示作用于柱塞上的慢时变外负载力，fd（t）=106+105sin（0.4πt）N，则d（t）=f˙d（t）/m=83.8cos（0.4πt）N。

利用以上得到的数据，对轧机液压伺服位置系统进行仿真，将结果与传统PID控制器获得的结果进行比较。所有的测试都是在相同的条件下进行的，仿真结果如图2～图5所示。图2显示了ASD控制系统的实时位置，实际位置和跟踪误差,可以看出具有优异的瞬态特性，跟踪误差在0.15s时间内快速趋向于0，具有良好的跟踪性能。图3显示出在相同条件下，传统PID控制系统跟踪效果不如ASD控制效果。考虑到功率最小化是控制系统的基本标准，从图4可以看到ASD控制器输出一个非常低的振幅和相当平滑的控制输入信号；而传统PID控制器需要更多的功率来实现跟踪。图5为ASD控制系统和PID控制系统的跟踪误差速度。可以看出，ASD控制系统瞬态状态非常好，持续时间小于0.1s。仿真结果表明了ASD控制器可以保证系统信号有界及系统的状态可以收敛到原点附近的范围内，验证了ASD方法的有效性。

表1 1450mm四辊可逆轧机液压伺服位置系统主要物理参数

图2 ASD控制系统位置及跟踪误差

图3 PID控制系统位置及跟踪误差

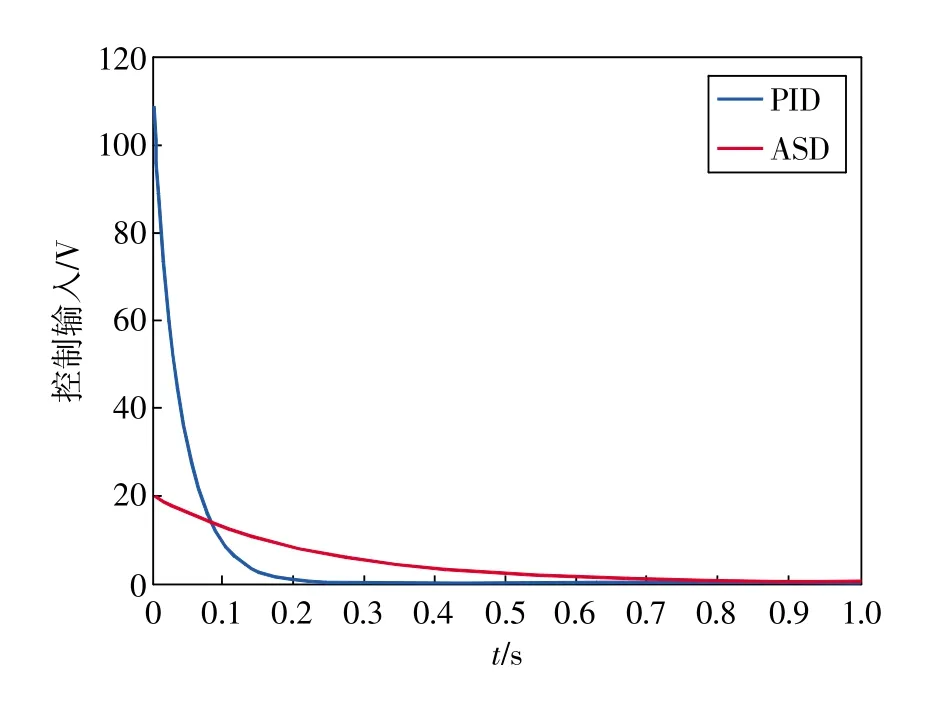
图4 控制器输入

图5 跟踪误差速度

4 结束语

本文针对具有参数不确定性、非线性模型和状态不可测的轧机液压伺服位置系统，提出一种基于ASD动态逆的控制算法，最后通过理论和仿真说明了在外部负载扰动大幅度变化和不确定性因素对系统的影响下，该控制器可以保证系统位置跟踪精度，满足轧机对液压伺服位置系统的要求。下一步将在轧机液压伺服位置系统的基础上，研究轧机厚度控制系统，进一步提高系统的稳定性和可靠性。

[1]杨瑞峰，郭明明，张鹏，等.PMSM位置伺服系统鲁棒控制技术研究[J].中国测试，2017，43（4）：89-94.

[2]XU Z，MA D，YAO J，et al.Feedback nonlinear robustcontrol forhydraulic system with disturbance compensation[J].Journal of Systems&Control Engineering，2016，230（9）：978-987.

[3]WON D，KIM W.Disturbance observer based backstepping for position control of electro-hydraulic systems[J].International Journal of Control，2015，13（2）：488-493.

[4]YANG G，YAO J，LE G，et al.Adaptive robust control of DC motors with time-varying output constraints[C]∥Control Conference（CCC），2015 34th Chinese.Hangzhou：IEEE，2015.

[5]KOVARI A.Effect of leakage in electrohydraulic servo systems based on complex nonlinear mathematical model and experimental results[J].Acta Polytechnica Hungarica，2015，12（3）：2015-2129.

[6]LOVREC D，TIC V，TASNER T.Simulation-aided determination ofan efficiency field asa basisfor maximum efficiency-controller design[J]. International Journal of Simulation Modelling，2015，14（4）：669-682.

[7]YAO J，JIAO Z，MA D，et al.High-accuracy tracking controlofhydraulic rotary actuators with modeling uncertainties[J].IEEE/ASME Transactions on Mechatronics，2014，19（2）：633-641.

[8]冯瑞琳，魏建华.粉末成形液压机自适应鲁棒运动控制[J].农业机械学报，2015，46（8）：352-360.

[9]YAO J，JIAO Z，MA D.A practical nonlinear adaptive control of hydraulic servomechanisms with periodic-like disturbances[J].IEEE/ASME Transactions on Mechatronics，2015，20（6）：2752-2760.

[10]KADDISSI C，KENNE J P，SAAD M.Identification and real-time control of an electrohydraulic servo system based on nonlinear backstepping[J].Mechatronics IEEE/ASME Transactions，2007，12（1）：12-22.

[11]YAO J，JIAO Z，MA D.Extended-state-observer-based output feedback nonlinear robust control of hydraulic systems with backstepping[J].IEEE Transactions on Industrial Electronics，2014，61（11）：6285-6293.

[12]KIM W，SHIN D，WON D，et al.Position tracking and flatnesscontrollerwith disturbance observerin hydraulic servo systems[C]∥Sice Annual Conference.Tokyo： IEEE，2011.

[13]方一鸣，许衍泽，李建雄.具有输入饱和的液压伺服位置系统自适应动态面控制[J].控制理论与应用，2014，31（4）：511-518.

[14]WANG C，QUAN L，ZHANG S，et al.Reduced-order modelbased active disturbance rejection controlof hydraulic servo system with singular value perturbation theory[J].Isa Transactions，2017，67（17）：455-465.

[15]GUAN C，PAN S.Adaptive sliding mode control of electrohydraulic system with nonlinear unknown parameters[J].Control Theory&Applications，2008，16（11）：1275-1284.

[16]QUAN Q，CAI K，LIN H.Additive-state-decompositionbased tracking control framework for a class of nonminimum phase systems with measurable nonlinearities and unknown disturbances[J].International Journal of Robust& Nonlinear Control，2015，25 （2）：163-178.

[17]赵微微，张磊，井延伟.变桨风力发电机组控制器优化设计[J].电网技术，2014，38（12）：3436-3440.