钢轨轨头内缺陷的超声相控阵DAC定量方法

戴万林，杨岳，刘希玲，梁佳佳，童林军



钢轨轨头内缺陷的超声相控阵DAC定量方法

戴万林1，杨岳1，刘希玲1，梁佳佳2，童林军3

(1. 中南大学 交通运输工程学院，湖南 长沙 410075；2. 武汉铁路局 武昌客车车辆段，湖北 武汉 430000；3. 萍乡学院，江西 萍乡 337055)

为改善钢轨现行超声检测方法效率低和定量评价难度大的不足，将传统单探头DAC曲线定量方法引入超声相控阵检测领域，研究一种基于超声相控阵全矩阵数据的轨头内部缺陷定量评价方法。对轨头检测断面进行网格划分，模拟各网格节点处缺陷尺寸。利用超声相控阵测量模型，求得各网格节点处的DAC曲线。基于Kriging插值方法，构建轨头缺陷DAC定量评价模型，实现对检测断面内任意位置缺陷的定量评价。通过搭建钢轨超声相控阵检测试验系统，对钢轨人工缺陷试块进行检测试验。研究结果表明：相比工业中常用的−6 dB缺陷定量方法，本文方法在轨头内部缺陷检测精度和效率上均有明显优势。

超声相控阵；钢轨轨头；距离幅度曲线(DAC)；Kriging插值法；缺陷定量

钢轨引导列车行进并承受列车重量，其完好状态是影响铁路行车安全的重要因素[1]。目前我国钢轨主要采用铸造轧制的生产工艺，在此过程中可能出现夹渣及缩孔等缺陷；使用中，受车轮反复碾压，容易在轨头内扩展形成疲劳斑痕和裂纹等缺陷，如不能及时有效地检出，将严重威胁铁路运输安全[2]。钢轨内部缺陷形态及取向复杂多变，传统的钢轨超声检测方法存在检测工作量大、效率低，且存在漏检和误检等问题[3]。超声相控阵技术可实现声束偏转、聚焦和扫描，能大大提高钢轨内部缺陷的检测精度和效率[4]。近年来，国内外学者和机构开展了大量相关研究，美国TTCI公司研制了Omni-scan超声相控阵系统[5]，用于轨头缺陷检测；Bredif等[6]利用超声仿真软件CIVA设计了一种对钢轨内部空隙率进行超声相控阵检测的工具；Zhao等[7]建立了一种利用超声相控阵检测钢轨焊接缺陷的模型。邬以三[8]采用现有的超声相控阵检测模型提出了钢轨缺陷超声检测的基本方案。卢超等[9]用超声相控阵方法对钢轨焊缝缺陷进行了实验研究。以上工作主要从钢轨超声相控阵检测技术的应用层面开展研究，尚未针对轨头深入开展其内部缺陷的超声相控阵高效准确定量方法研究。为了提高轨头内部缺陷检测的效率和精度，本文借鉴单晶超声换能器DAC缺陷定量思想[10−11]，结合超声相控阵测量模型和全矩阵数据获取理论，利用Kriging插值方法简化缺陷定量过程，研究一种轨头内部缺陷的超声相控阵快速精确定量方法。

1 轨头缺陷超声相控阵检测基本理论

1.1 超声相控阵测量模型

采用接触法进行轨头超声相控阵检测时，因轨头表面曲率较小，换能器布置在其表面，直接通过耦合剂传递声能，如图1。

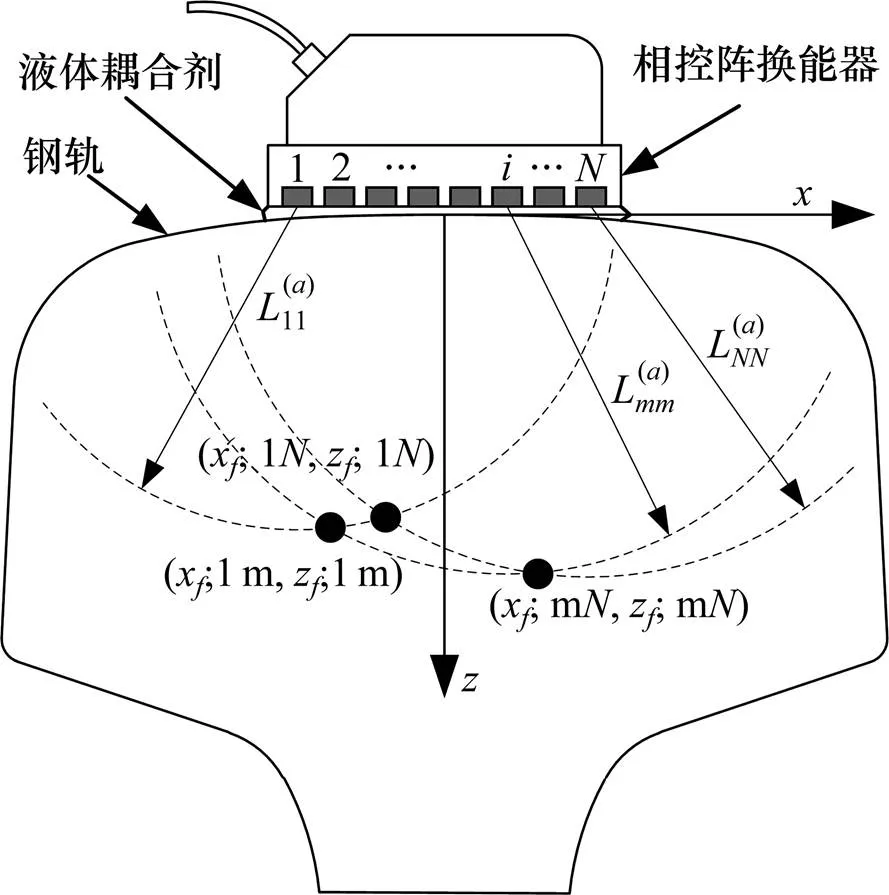
图1 轨头内部缺陷定位方法

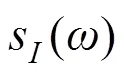
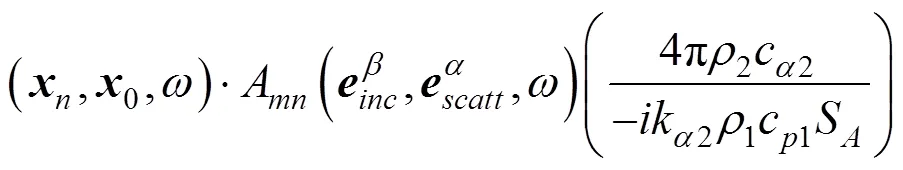
1.2 缺陷回波特征信息提取

由式(1)可知，缺陷的精确定量需要精确提取缺陷二维位置信息和回波幅值。本文采用全矩阵回波数据中所有阵元自发自收的A波对缺陷进行定位，如图1，第阵元中心到缺陷的距离为：

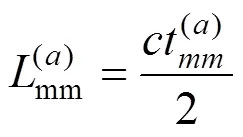
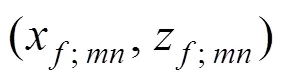
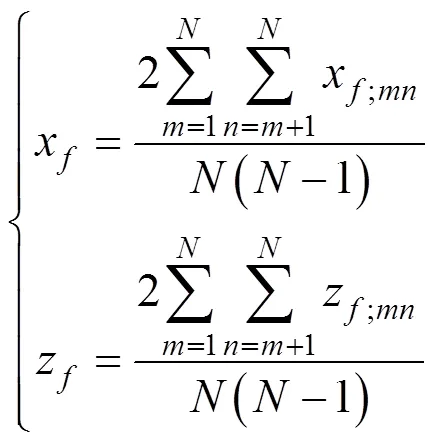
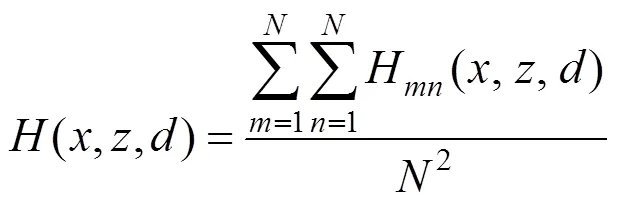
2 轨头缺陷超声相控阵定量评价模型

2.1 超声相控阵DAC曲线簇

超声相控阵DAC定量的思想，即研究超声相控阵检测中缺陷二维位置信息、回波幅值特性及当量尺寸之间的关系[14]。将轨头划分网格点，假定缺陷二维位置，如图2，变化一系列直径，利用式(1)分别计算每个网格点的缺陷回波幅值特性，建立所有节点处的DAC曲线簇。

图2 轨头检测区域网格节点划分

2.2 DAC曲线的Kriging空间插值

若缺陷出现在非网格点上，则不能直接采用DAC定量。且声场建模涉及大量多元高斯叠加计算，若继续细化网格将会带来指数式增长的计算量。所以考虑利用已有网格点处的数据进行任意点DAC曲线的插值计算。由于Kriging插值方法具有精度高，适应性强的优势[15]，故选择Kriging插值法。典型Kriging插值由多项式估计值和偏差2部分构成[16−17]：

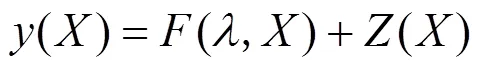
式中：为自变量空间；(,)为关于的回归模型，利用式(7)求解；()为点的估计偏差；为回归系数。

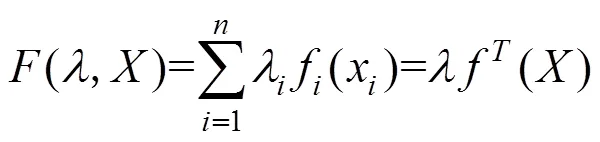
式中：为样本点数目；()为一组基函数。

()是期望值为0，方差为常数2的随机过程，任意2点间的协方差为：

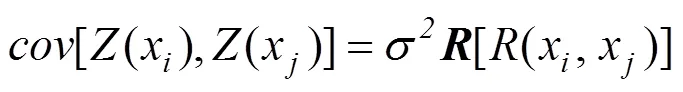
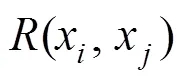
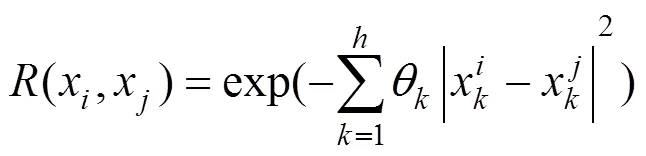
2.3 轨头缺陷DAC定量评价模型

选择方向−30~30 mm，方向5~40 mm作为采样区域，按照5 mm步长对该区域进行网格划分。因缺陷分布关于轴对称，所以仅需计算方向0~30 mm的数据。模拟缺陷当量尺寸0.3~6 mm，步长为0.3 mm。利用式(1)计算得到1 120组缺陷坐标信息、回波幅值特性和当量尺寸的样本数据，见表1。绘制超声相控阵DAC曲线簇，此处仅将部分曲线簇进行展示，如图3。

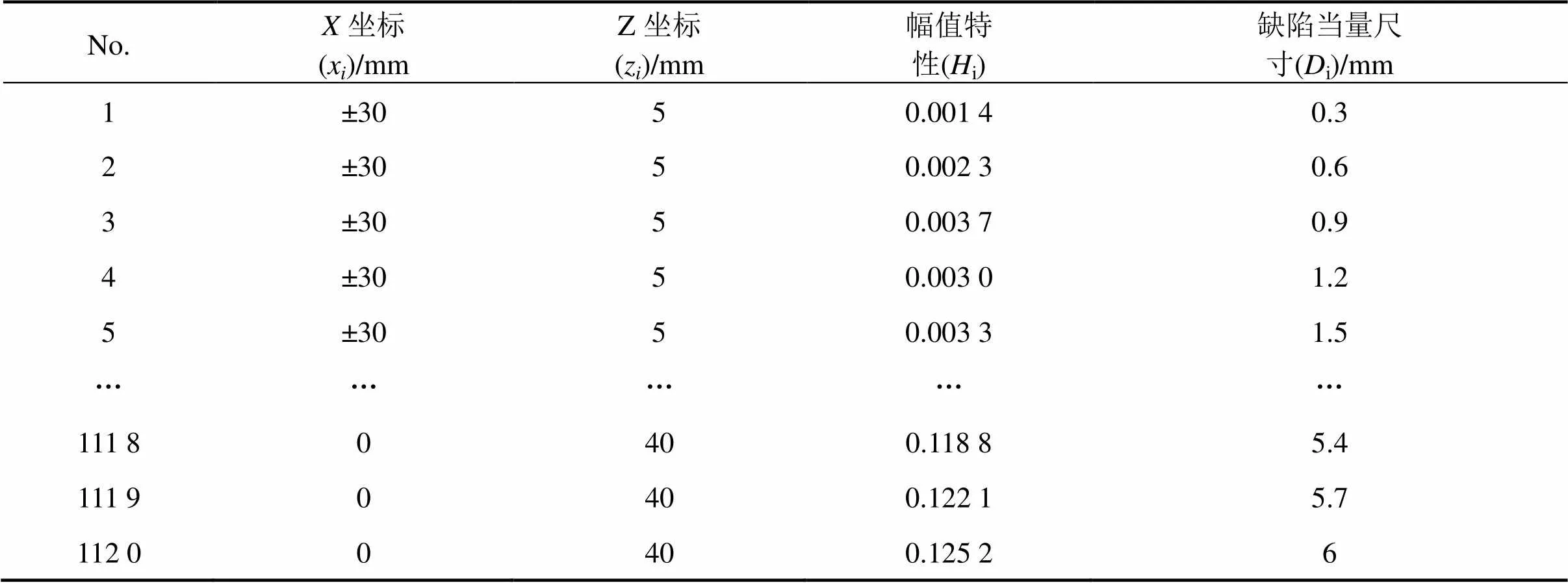
表1 Kriging模型样本数据

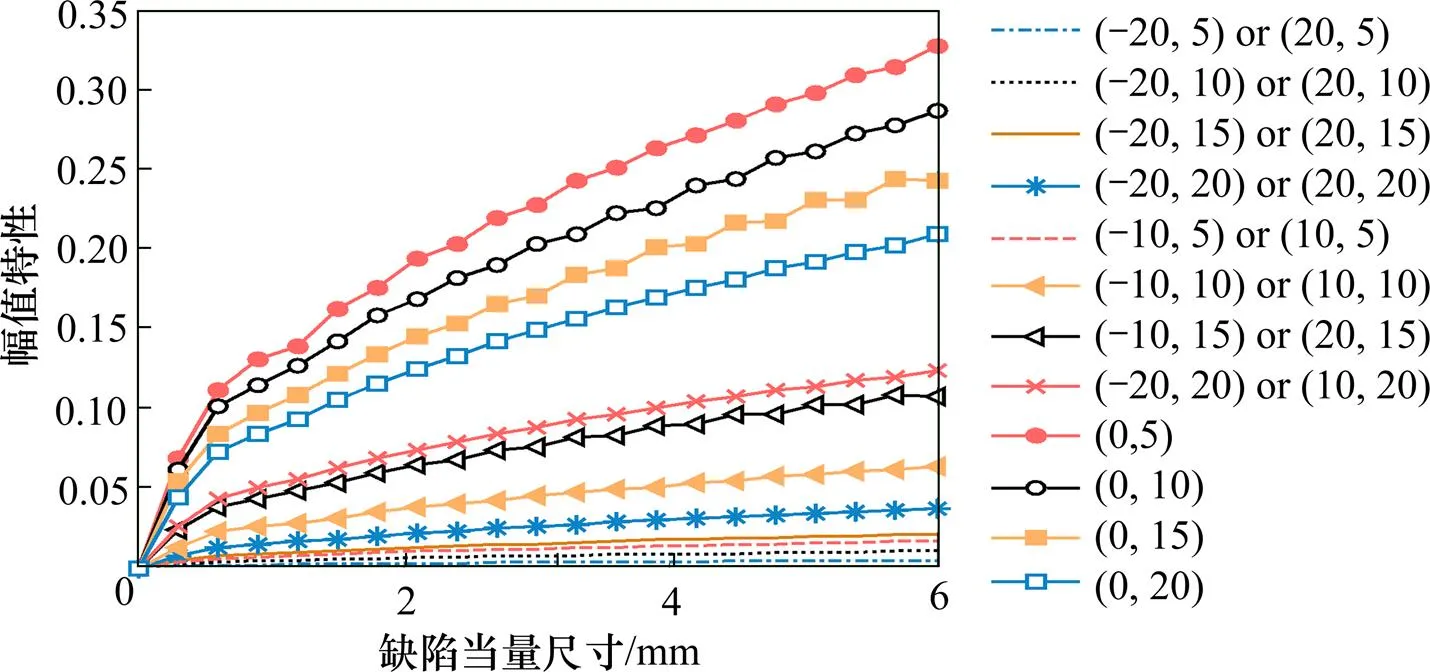
图3 超声相控阵DAC曲线簇

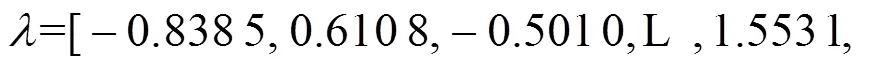
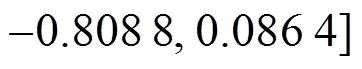
利用式(10)计算相关系数为：

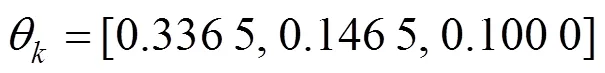
利用色度图表示轨头缺陷DAC定量评价模型中自变量与因变量的关系，如图4。

2.4 模型精度分析

使用如式(11)的均方根误差()方法[17]，对缺陷DAC定量评价模型进行精度检验。

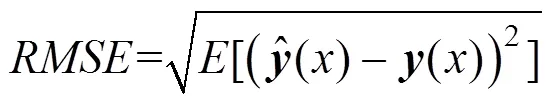
经计算，评价模型的RMSE值为7.994 0×10−4，这表明构造的模型精度较高。

3 轨头缺陷检测试验

3.1 检测系统

搭建轨头超声相控阵检测系统，如图5。

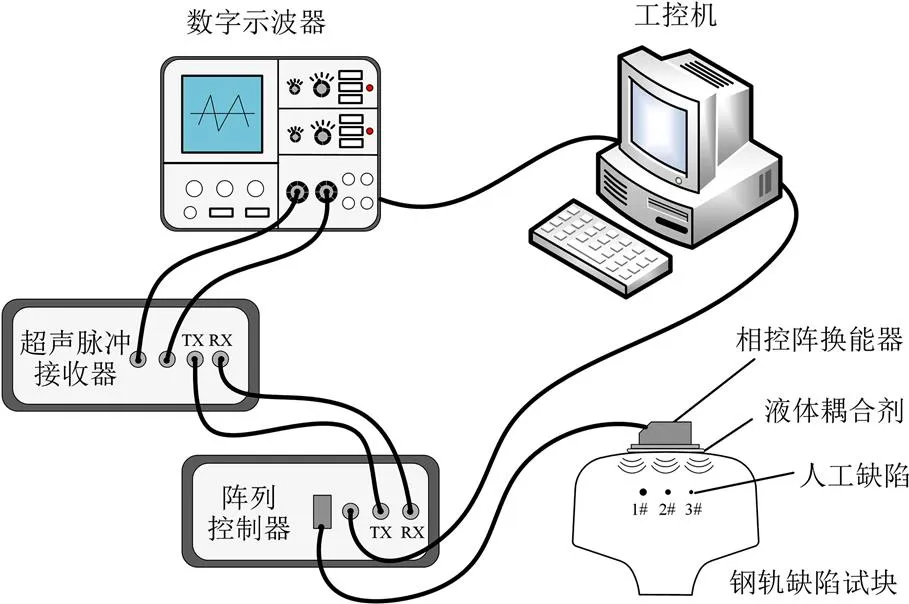
图5 超声相控阵钢轨检测系统

采用中心频率为5 MHz的商用32阵元线性阵列相控阵换能器，阵元间隙0.2 mm，阵元宽度0.8 mm，采样频率100 MHz，采样长度16ms。检测时，手动将相控阵换能器放置于轨头表面，通过耦合剂进行耦合。

3.2 钢轨人工缺陷试块

设计并制作如图6的钢轨人工缺陷试块，共3个横通孔，3个孔的直径依次为4，3和2 mm，编号为1号，2号和3号缺陷。检测时，相控阵换能器的对称轴与试块对称轴重合放置，如图2。

3.3 试验数据采集

利用建立的检测系统进行检测试验，采集全矩阵回波数据。将全矩阵回波中所有阵元自发自收的A波进行展示，如图7。

图7中，可观察到32组A波数据的缺陷回波，形成了各阵元对缺陷的延迟响应情况。其中，第16阵元自发自收的时域A波如图8。

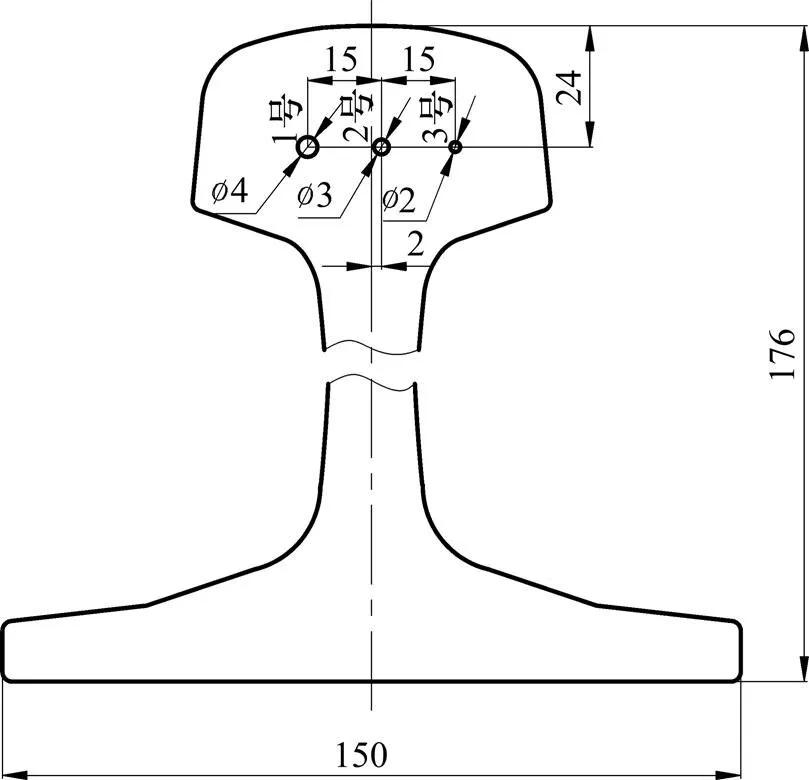
图6 钢轨人工缺陷试块

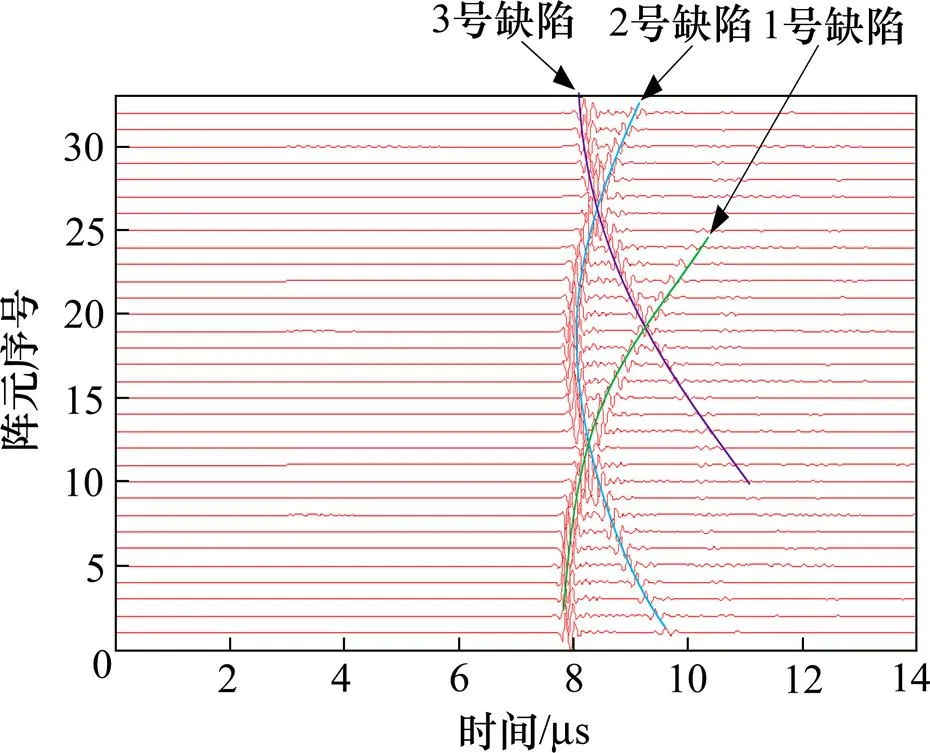
图7 采集的A波簇分析

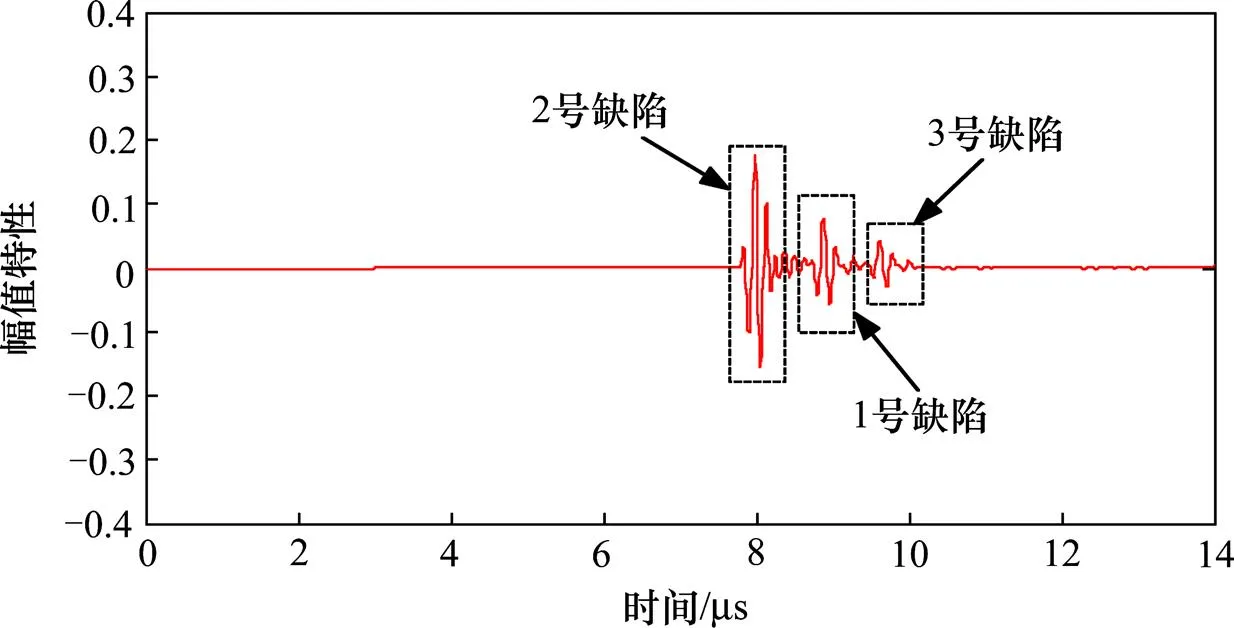
图8 第16阵元自发自收时域A波信号

4 试验结果与分析

4.1 试验结果

针对轨头缺陷试块的3个缺陷，提取图7每个缺陷波的前沿时刻，利用式(3)，式(4)和图1中的缺陷定位方法得到缺陷二维坐标分别为：1号 (−13.337 1, 23.801 2)，2号(2.328 0, 23.940 1)，3号(17.233 0, 23.821 6)。

对轨头各网格节点处的DAC曲线簇进行Kriging插值，分别求得3个缺陷位置对应的DAC曲线如图9。

图9 缺陷位置处Kriging插值所得DAC曲线

按照式(5)计算3个缺陷的缺陷波幅值特性分别为0.073 8，0.126 1和0.033 7。根据对应点处的DAC曲线求得3个缺陷的当量尺寸，见表2。

表2 本文方法与−6 dB方法缺陷定量结果对比

4.2 检测精度与效率分析

为验证本文建立的轨头缺陷DAC定量评价模型的有效性，将其对缺陷的定量结果和效率分别与工业检测常用−6 dB缺陷定量方法[18]进行对比。因为全聚焦成像具有分辨率高的特点，为了增强对比效果，采用全聚焦−6 dB方法。首先基于全聚焦延时法则对获取的全矩阵数据进行全聚焦成像，如图10，并进行缺陷定量计算，将其定量结果和效率分别与本文方法进行如表2和图11的对比分析。

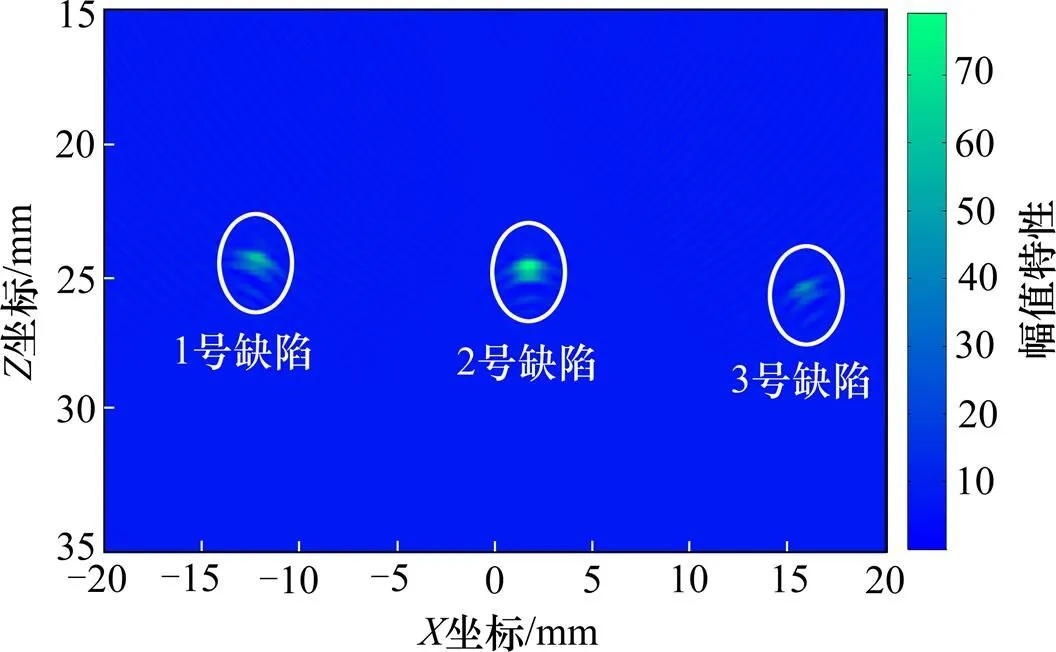
图10 轨头缺陷超声相控阵全聚焦成像

图11 本文方法与全聚焦−6 dB方法计算效率对比

针对同一缺陷，相比−6 dB方法，采用本文方法的定量误差由约30%减小到约5%。且因为省去了高精度成像花费的大量时间，本文方法相比于−6 dB方法具有模型建立快的优势，同时应用于轨头连续检测时无需重复建模。故在求解精度和效率方面，本文提出的轨头缺陷DAC定量评价方法均优于全聚焦−6 dB定量方法。

5 结论

1) 基于超声相控阵测量模型，通过Kriging插值构建超声相控阵DAC定量评价模型，实现了轨头断面任意位置处缺陷的快速精确定量评价。

2) 与传统的−6 dB方法相比，本文提出的轨头内部缺陷超声相控阵DAC定量方法具有更高的效率和精度，具有良好的工程应用价值。

3) 本文方法适用于轨头内部常出现的白点、缩孔、气孔、夹渣等体积型缺陷的精确定量问题。对于裂纹等面积型缺陷的精确定量，需根据实际经验，沿其扩展方向离散成若干体积型缺陷进行定量，将在后续工作中进行深入研究。

4) 缺陷定位定量结果存在误差的原因有：①实际检测时超声相控阵换能器的中心轴线未能与轨头对称轴线完全重合；②缺陷波的前沿提取不精确；③式(1)中测量模型的系统函数存在不可避免的误差。后续的工作中会考虑添加补偿算法来进一步提高检测精度。

[1] LIU X, Lovett A, Dick T, et al. Optimization of ultrasonic rail-defect inspection for improving railway transportation safety and efficiency[J]. Journal of Transportation Engineering, 2014, 140(10): 1−10.

[2] 张书增, 李雄兵, 杨岳, 等. 钢轨轨头内多元高斯声场模拟及其缺陷响应[J]. 铁道学报, 2014, 36(1): 76−80. ZHANG Shuzeng, LI Xiongbing, YANG Yue, et al. Multi-Gaussian beam simulation and flaw response for rail head[J]. Journal of the China Railway Society, 2014, 36(1): 76−80.

[3] 刘希玲, 张荣繁, 胡宏伟, 等. 机车车轮超声自动检测系统设计[J]. 铁道科学与工程学报, 2014, 11(6): 122−126. LIU Xiling, ZHANG Rongfan, HU Hongwei, et al. Design of ultrasonic automatic testing system for locomotive wheels[J]. Journal of Railway Science and Engineering, 2014, 11(6): 122−126.

[4] Caroline Holmes, Bruce W D, Paul D W. Post-processing of the full matrix of ultrasonic transmit–receive array data for non-destructive evaluation[J]. NDT & E International, 2005, 38(8): 701−711.

[5] Garcia G, ZHANG J. Application of ultrasonic phased arrays for rail flaw inspection[R]. Washington. DC: Office of Research and Development, 2006: 31−37.

[6] Bredif P, Plu J, Pouligny P, et al. Phased-array method for the ut-inspection of french rail repairs[C]// Review of Progress in Quantitative Nondestructive Evaluation: 34th Annual Review of Progress in Quantitative Nondestr- uctive Evaluation. AIP Publishing, 2008, 975(1): 762− 769.

[7] Zhao L, Rudlin J. Development of an advanced ultrasonic inspection tool for rapid volumetric examination of aluminothermic rail welds[C]// Nondestructive Evaluation/Testing (FENDT), 2014 IEEE Far East Forum on. IEEE, 2014: 354−357.

[8] 邬以三. 超声相控阵钢轨探伤方法研究[D]. 广州: 华南理工大学, 2011. WU Yisan. Study on the method of rail flaws detection using ultrasonic phased array[D]. Guangzhou: South China University of Technology, 2011.

[9] 卢超, 邓丹, 陈文生, 等. 钢轨气压焊接头的超声相控阵检测技术研究[J]. 失效分析与预防, 2011, 6(3): 139− 143. LU Chao, DENG Dan, CHEN Wensheng, et al. Research on ultrasonic phased array detecting technique for gas pressure welding joint of rail[J]. Failure Analysis & Prevention, 2011, 6(3): 139−143.

[10] 杨岳, 戴万林, 李雄兵, 等. 镁合金壳体内部缺陷的精确超声定量方法[J]. 中国有色金属学报, 2015, 25(10): 2666−2671. YANG Yue, DAI Wanlin, LI Xiongbing, et al. Ultrasonic method for accurately sizing flaws in magnesium alloy shell[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(10): 2666−2671.

[11] Schmerr L W, Song J S. Ultrasonic nondestructive evaluation systems: models and measurements[M]. New York: Springer, 2007.

[12] Huang R, Schmerr L W. Characterization of the system functions of ultrasonic linear phased array inspection systems[J]. Ultrasonics, 2009, 49(2): 219−225.

[13] Jeong H, Schmerr L W. Ultrasonic transducer fields modeled with a modular multi-Gaussian beam and application to a contact angle beam testing[J]. Research in Nondestructive Evaluation, 2008, 19(2): 87−103.

[14] Schmerr L W. Fundamentals of ultrasonic phased arrays[M]. New York: Springer, 2014.

[15] Rennen G. Subset selection from large datasets for Kriging modeling[J]. Structural & Multidisciplinary Optimization, 2009, 38(6): 545−569.

[16] ZENG W, YANG Y, XIE H, et al. CF-Kriging surrogate model based on the combination forecasting method[J]. Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science, 2015, 230(18): 3274−3284.

[17] 王兆国, 程顺有, 刘财. 地球物理勘探中几种二维插值方法的误差分析[J]. 吉林大学学报, 2013, 43(6): 1997−2004. WANG Zhaoguo, CHENG Shunyou, LIU Cai. Error analysis of several two-dimensional interpolation methods in the geophysical exploration[J]. Journal of Jilin University, 2013, 43(6): 1997−2004.

[18] 周正干, 彭地, 李洋, 等. 相控阵超声检测技术中的全聚焦成像算法及其校准研究[J]. 机械工程学报, 2015, 51(10): 1−7. ZHOU Zhenggan, PENG Di, LI Yang, et al. Research on phased array ultrasonic total focusing method and its calibration[J]. Journal of Mechanical Engineering, 2015, 51(10): 1−7.

DAC quantitative method of ultrasonic phased array for rail head defects

DAI Wanlin1, YANG Yue1,LIU Xiling1, LIANG Jiajia2, TONG Linjun3

(1. School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China; 2. Wuchang Vehicles Section, Wuhan Railways Bureau, Wuhan 430000, China; 3. Pingxiang University, Pingxiang 337042, China)

In order to improve the low efficiency and high challenge in defects quantitative of current ultrasonic testing method for rail, the traditional quantitative method using distance amplitude curve of monolithic transducer is introduced into ultrasonic phased array detection. A method using full matrix data of ultrasonic phased array is studied for quantitative evaluation of rail head internal defects. The detecting section of the rail head is partitioned, a series of defects size at the nodes are simulated, and the distance amplitude curves at the nodes were obtained by the ultrasonic phased array measurement model. The distance amplitude curve quantitative evaluation model of rail head internal defects is constructed based on the Kriging interpolation method, and make it possible to quantitatively evaluate defects of any position in the detecting section. The ultrasonic testing system for rail was built to test the artificial defects in the rail test block. The results show that the proposed method has obvious advantages in accuracy and efficiency when detecting defects compared with the commonly used -6dB defects quantitative method in industry.

ultrasonic phased array; rail head; distance amplitude curve (DAC); Kriging interpolation; defect quantification

U216.3

A

1672 − 7029(2018)01 − 0188 − 08

2016−12−25

国家自然科学基金资助项目(61271356，51575541)；湖南省自然科学基金资助项目(2015JJ2168，14JJ2002)；中南大学中央高校基本科研业务费专项资金资助项目(2016zzts335)；中国铁路总公司科技研究开发计划资助项目(2014G001-E)

杨岳(1962−)，男，湖南常德人，教授，博士，从事交通装备数字化设计制造、智能维护与超声无损检测研究；E−mail：yangyue@csu.edu.cn