有限云模型和距离判别法在边坡稳定性评价中的应用

戴兴国，张彪，闫泽正

有限云模型和距离判别法在边坡稳定性评价中的应用

戴兴国，张彪，闫泽正

(中南大学 资源与安全工程学院，湖南 长沙 410083)

边坡稳定性分类是一个综合的不确定系统问题，针对指标分布和等级边界模糊的特点，提出一种以有限区间下的云模型为评价主体、距离判别法确定指标权重的稳定性分类的方法。给出有限云模型的相关概念及计算模型，再介绍具体的赋权的原理及流程。引用相关文献的评价指标体系，结合隶属函数计算出各等级的基本概率分配(BPA)，并依据指标间距离确定指标权重；再依据改进的云模型计算各评价因子隶属于不同等级的云特征参数，并结合评价指标权重和云发生器，得到评价样本的综合确定度，实现边坡稳定性等级的划分，与其它理论方法对比分析。研究结果表明：该模型应用于边坡稳定性分级是有效可行的，能弥补传统云理论不能整体上描述有限区间下的指标间的确定与不确定性关系的缺陷，提高云模型应用的普适性。

边坡稳定性；距离判别；隶属函数；基本概率分配；有限云模型；综合确定度

随着中国城市化建设的快速推进，相应的基础设施建设规模和数量也迅速加大，如公路、铁路、桥梁以及隧道等，边坡稳定性评估成为这些工程涉及的一个基本问题。边坡稳定性评价直接关乎人类生命财产安全以及工程施工合理性和整个工程的成败，近几年已受到工程界和学术界的重视。为此，许多学者和专家基于不同的理论对边坡稳定性进行探讨，如基于PEM—JFEM耦合理论[1]，模糊综合评判法[2]，耦合的BP神经网络 法[3−4]，可拓法[5−6]和云模型理论[7−8]等的边坡稳定性评价方法，这些方法在一定程度上促进了理论研究和工程实践。但以上方法很少能同时兼顾边坡稳定性评价的模糊性、不确定性及随机性，而与工程实际情况不符，在理论应用推广上存有一定的障碍或局限性，如PEM—JFEM方法对于数值模型的边界条件难以确定，岩土参数的设定带有极大的模糊性，很难反映真实状况；模糊数学法在实际应用过程中隶属函数难以确定；耦合的神经网络法在实际中很难获取大量具有代表性的样本，并且会因为网络学习了过多的样本细节而导致“过拟合”的现象；可拓法会忽略重要的约束条件，计算出的负关联度在工程实践中没有现实意义；传统的云模型理论受限于评价指标须服从无限区间分布的特征，往往实际中评价指标的分布并非完全服从正态分布，简而言之，当评价等级为单边区间形如[0,]或[,+∞ ]时，依然用正态分布表示显然与实际不符，从而导致这些理论方法局限性。基于此，在结合已有理论成果的基础上，提出有限区间下的云模型方法在边坡稳定性评价中的应用模型，结合实际统计指标服从均匀分布和正态分布的特点，改进传统的云模型假设评价指标分布均为正态分布的缺陷，在有限区间下讨论云模型，避免模拟结果脱离实际的可能性，提高该方法应用于同类工程中的适应性、可靠性和普适性；运用证据距离判别法求取指标权重，增加了实践应用过程中的可操作性。本文从新的角度探讨云模型，以促进边坡稳定性分类结果与实际情况更相符。

1 理论基础

1.1 正态隶属函数

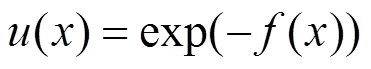
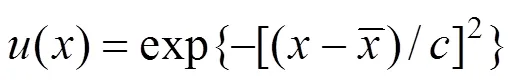
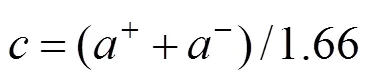
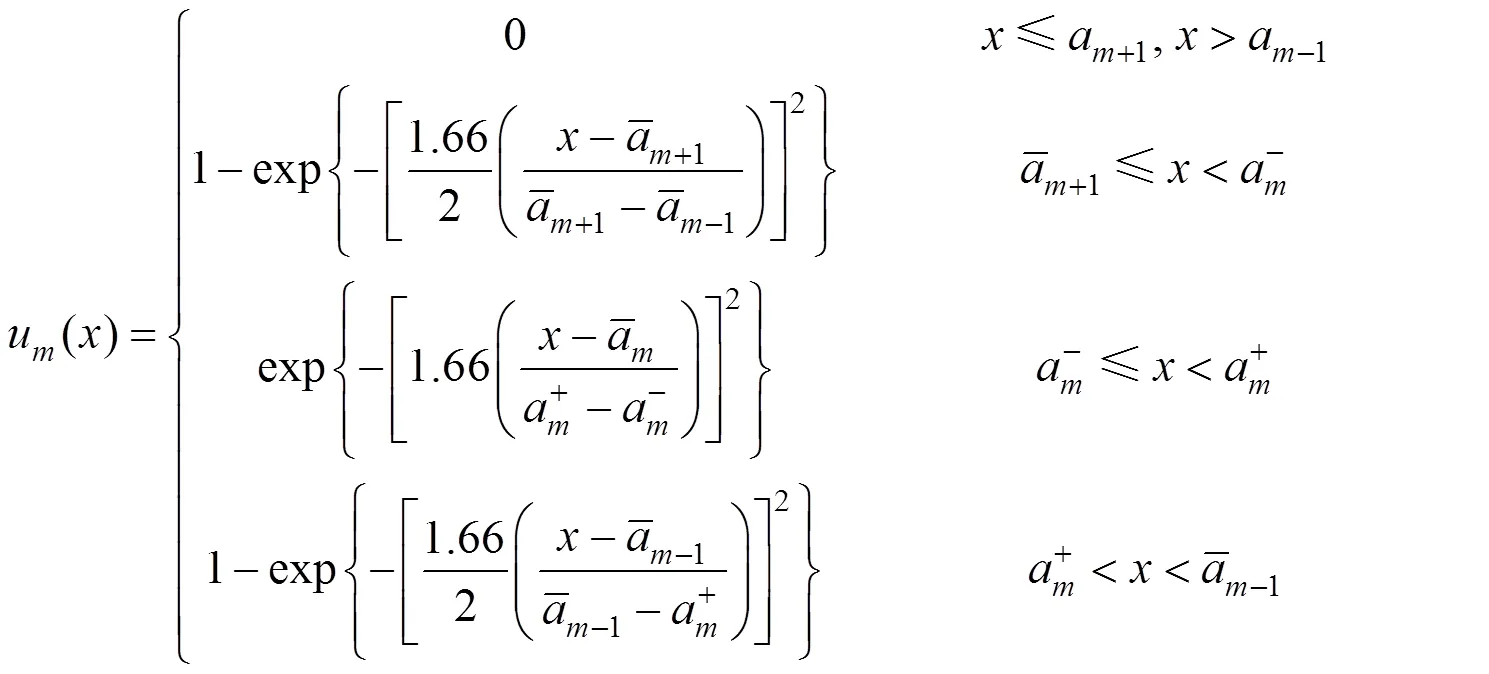
同理可推得越小越优性指标的计算公式如 式(3)。

1.2 识别框架和BPA

对于某一判决问题的所有可能答案组成一个集合，在集合中各元素彼此排斥，在特定条件下，问题答案只能是集合中的唯一元素，为此Shafer根据集合论将此互斥完备集合Θ称为识别框架[10−11]，可记为：

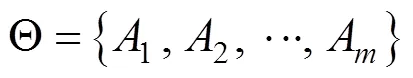
式中：A类似于评价集中的评价等级。

证据集就是判断某一问题所属识别框架Θ某个子集的依据，相当于评价中的指标因素，记为：

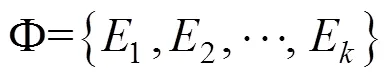
在识别框架Θ中，基本概率分配函数(Basic Probability Assignment)[10]是集合2Θ到[0，1]的映射，且满足:

1.3 有限云模型

云模型[12−14]是在模糊数学和统计学的基础上发展起来的一种描述不确定性关系的数学方法，将不确定性、模糊性和随机性相结合，构成定性和定量描述之间的相互映射关系，作为定性语言和定量语言的转换基础，是实现定性定量相互转化的重要媒介，广泛应用在各工程领域的评价和预测 中[7−8, 15−16]。边坡稳定性评价问题具有不确定和随机性以及模糊性特点，应用传统云模型虽能反映评价指标的模糊性和随机性，但其应用的理想前提是指标服从正态分布，但事实上指标的分布并非完全服从正态分布，而是服从有限区间下的正态分布，故而应用理想的云模型反映的模拟对象的特征与实际情况有所差异。为了真实反映实际边坡稳定性评价指标的分布特点，故而对以往的云模型加以修正和改进，提出有限区间下的云模型的概念和计算模型。

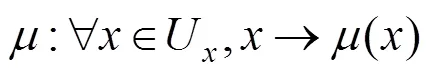
则在论域上的分布称为云，每一个称为一个云滴，并用期望E、熵E和超熵H3个特征值来表征这一概念[12]。

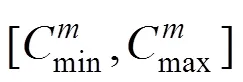
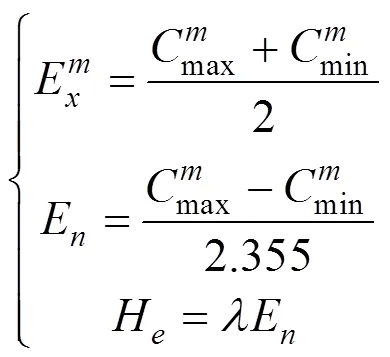
1.4 有限云发生器

1;

1;

1;

1

1(1)11;

()()11;

1()或

1()exp{((1()1^2)/(2*1^2)};

1()1;

End

End

2 有限云模型和距离判别赋权模型的构建

2.1 距离判别赋权的算法及流程

在整个边坡稳定性评价过程中，云模型理论构成整个评价体系的主体，而权重的赋值成为了分类结果是否合理的关键，因此，则需要引入正态隶属度和基本概率分配耦合赋权的方法展开研究。基本概率分配可以反映评价指标的模糊性，采用距离判别法求取权重可以综合考虑各指标各等级间的相互影响程度，相较于其他赋权方法，综合考虑各指标各等级间的相互影响程度，使确定的权重相对更加合理，其主要计算流程如下：

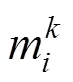
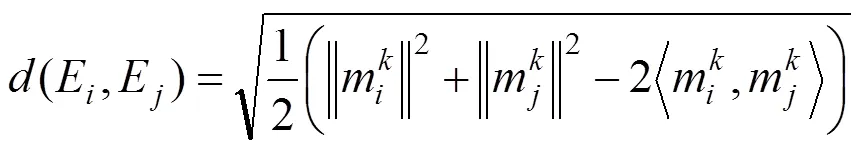
Step 4：指标支持度计算。由式(9)可知指标间的距离越小，相似度就越大，指标间的一致性就越好，指标被其它指标支持程度就越高，指标的支持程度可由下式来表示：

Step 5：权重计算。经归一化后，可得指标E的可信度(E)。

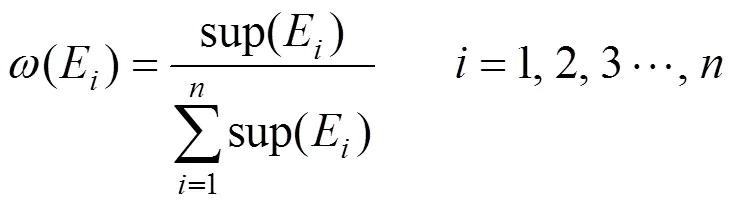
可信度(E)为指标E的权重，并满足归一化。

2.2 综合确定度

基于以上计算规则，可以计算某指标实测值0隶属于某个等级云的隶属度；再结合各指标的权重，便可计算出样本指标的综合确定度：

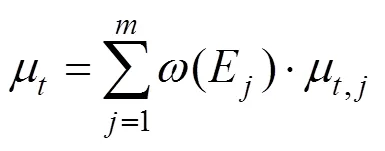
式中：为样本的第个指标的实测值所处于等级的确定度；(E)记为样本的第个指标的权重。参照综合确定度取值，按最大隶属原则可得出最终的隶属等级：

2.3 分级方法的算法流程

基于有限云模型边坡稳定性评价模型，建立合理的评价指标体系及其相应的评价标准，采用距离判别法来确定指标权重；根据已建立的评价指标标准，计算出各等级的云特征参数，通过正向有限云发生器生成云模型图，并计算实测指标隶属于某个等级的确定度；最后求出边坡稳定性的综合确定度，按照最大隶属原则得出边坡稳定性等级。本模型的具体算法流程如图1所示。

图1 边坡稳定性评价流程图

3 工程实例应用

3.1 评价指标选取及云滴图生成

影响边坡稳定性的因素错综复杂，最主要的因素可划分为工程条件、水文地质结构和外界环境扰动3大类。迄今为止，边坡稳定性评价指标的选取在工程界和学术界都尚未达成统一的标准，现行的做法通常是经验选取法，依据不同的研究对象制定不同的评价标准。由于评价指标选择的合理与否直接关系到最终结果的可靠性，因此在建立分类标准体系时应满足系统性、代表性、层次性、存异性、易获取和易量化等6项原则[18]。

为了验证本方法的可靠性和有效性，以文献[19]的桂柳高速公路K409+390~+528上行线边坡作为研究背景，并引用其指标体系以及实测数据加以验证和对比分析。实例选取了边坡高度、边坡坡角、岩石软化系数、岩土风化程度、年内旬最大降雨量等11个指标作为边坡稳定性评价指标，其边坡稳定性评价标准及其相应的指标实测值如表1所 示[19]。

基于有限云模型确定的云特征参数E，E和H，运用有限云发生器分别生成个指标的云滴图，如图2所示，横坐标表示评价指标取值变量纵坐标表示评价指标确定度。

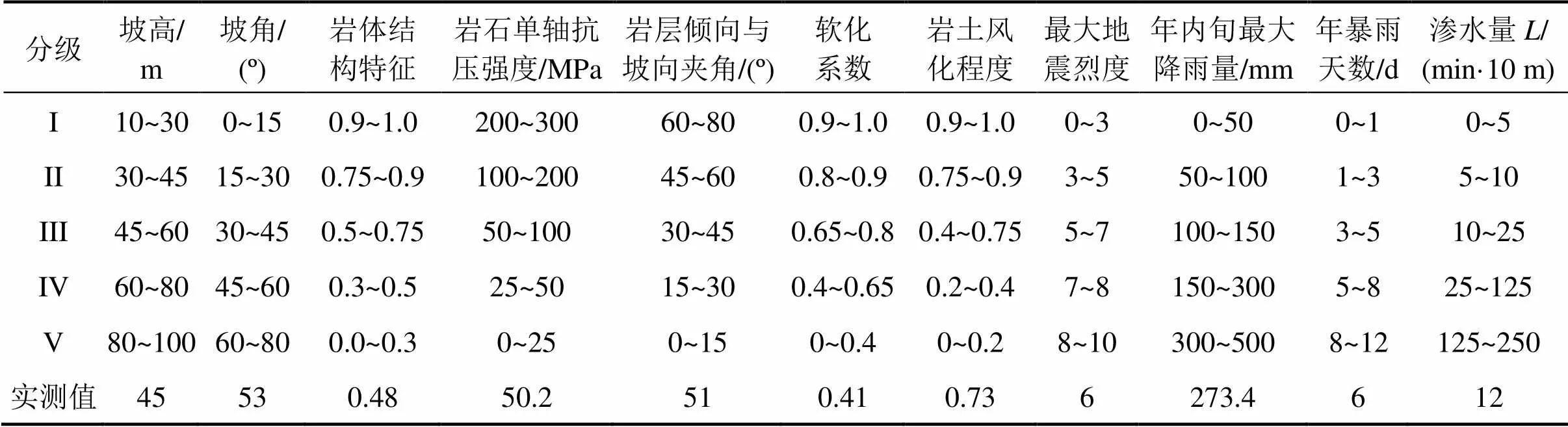
表1 单因素边坡稳定性评价标准及指标实测值

表2 各评价指标权值

图2 评价指标隶属于各级别的云滴图

3.2 指标权重确定

根据表1的评价标准和指标实测值，利用式(3)的隶属函数得各指标所属各等级的基本概率分配，再依据本文2.1节确定权重的方法求出各指标的权重如表2所示(受限于篇幅，具体中间步骤的运算结果在此不再给出)。

3.3 评价等级划分

表3 分级结果及对比

由表3可知，本模型分类结果与其它方法分类结果相吻合，表明该理论模型在一定程度上是正确可行的，另外，从表3中还可得出：最终的评价等级归属和倾向性，该边坡最终被划分到4等级，偏向于3等级，能对边坡的治理提供更多的参考信息，此外，评价结果还表明该段边坡不稳定，可以对其使用锚杆、锚索和喷混凝土加固，网格梁支护等基础处理措施，以满足工程安全稳定的要求，以防止发生安全事故。

边坡稳定性是一个定性概念，等级划分受到诸多不确定性因素影响和控制，利用有限云发生器，将其模糊性与随机性转化为确定度，揭露了评价过程中的模糊性与随机性。另外，边坡稳定性评估指标的实际分布形式对评价结果会有影响，将均匀分布与正态分布相结合生成的云模型反映实际情况更为合理。本文仅讨论了指标属于均匀分布和正态分布的情况，如何设置云特征参数使其计算出的综合确定度之和等于1还需更进一步的研究，简而言之，若提前划分好评价等级后，无论划分为几个等级，最终评价结果应完全落在这些区间里(综合确定度总和为1)，理想状态下不会发生最终确定度和小于或大于1的情况，从这个角度来讲该方法尚需进一步完善。

4 结论

1) 运用正态隶属函数确定各等级的基本概率分配，可实践性强，而且分配概率也合理。在确定指标权重时，从所属各等级隶属度间的距离出发，综合考虑各指标各等级间的相互影响程度，得出指标间的支持度，进而确定权重，避免了只考虑单个指标的缺陷，使确定的权重更加科学合理。

2) 改进传统云模型假设指标只服从正态分布的特点，在有限区间下探讨不同等级之间的模糊性和指标间及其分类标准间的确定与不确定关系，将分类界限模糊化，避免边界界限值导致分析结果偏离实际的风险。

3) 运用实例来验证本模型的正确性和适用性，并与其它方法的评价结果进行比较分析，实例表明有限区间下的云模型理论在基本概率分配与权重确定上更科学，分类结果更合理，并且实现过程易于编程，该理论为道路工程中的边坡稳定性评价提供了新的思路与途径。

[1] 肖术, 吴顺川, 高永涛, 等. 基于PEM−JFEM方法的节理岩质边坡稳定性评价[J]. 工程科学学报, 2015, 37(7): 844−850.

XIAO Shu, WU Shunchuan, GAO Yongtao, et al. Jointed rock slope stability evaluation based on PEM−JFEM method[J]. Chinese Journal of Engineering, 2015, 37(7): 844−850.

[2] 张勇慧, 李红旭, 盛谦, 等. 基于模糊综合评判的公路岩质边坡稳定性分级研究[J]. 岩土力学, 2010, 31(10): 3151−3156.

ZHANG Yonghui, LI Hongxu, SHENG Qian, et al. Study of stability gradation of highway rock slopes based on fuzzy comprehensive evaluation[J]. Rock and Soil Mechanics, 2010, 31(10): 3151−3156.

[3] 刘思思, 赵明华, 杨明辉, 等. 基于自组织神经网络与遗传算法的边坡稳定性分析方法[J]. 湖南大学学报(自科版), 2008, 35(12): 7−12.

LIU Shishi, ZHAO Minghua, YANG Minghui, et al. Slope stability analysis method based on self−organizing neural network and genetic algorithm[J]. Journal of Hunan University (Natural Sciences), 2008, 35(12): 7− 12.

[4] 胡军, 董建华, 王凯凯, 等. 边坡稳定性的CPSO−BP模型研究[J]. 岩土力学, 2016, 37(增): 577−582.

HU Jun, DONG Jianhua, WANG Kaikai, et al. Research on CPSO-BP model of slope stability[J]. Rock and Soil Mechanics, 2016, 37(Suppl): 577−582.

[5] 王新民, 康虔, 秦健春, 等. 层次分析法−可拓学模型在岩质边坡稳定性安全评价中的应用[J]. 中南大学学报(自然科学版), 2013, 44(6): 2455−2462.

WANG Xinmin, KANG Qian, QIN Jianchun, et al. Application of AHP-extenics model to safety evaluation of rock slope stability[J]. Journal of Central South University (Science and Technology), 2013, 44(6): 2455−2462.

[6] 谈小龙, 徐卫亚, 梁桂兰. 可拓方法在岩石边坡整体安全评价中的应用[J]. 岩石力学与工程学报, 2009, 28(12): 2503−2509.

TAN Xiaolong, XU Weiya, LIANG Guilan. Application of extenics method to comprehensive safety evaluation of rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(12): 2504−2509.

[7] 赵军, 宋扬. 改进熵权−正态云模型在边坡稳定性评价中的应用[J]. 水电能源科学, 2016(4): 120−122.

ZHAO Jun, SONG Yang. Slope stability evaluation based on improved entropy weight-cloud model[J]. Water Resources and Power, 2016(4): 120−122.

[8] 张军, 陈征宙, 刘登峰. 基于云模型的岩质边坡稳定性评估研究[J]. 水文地质工程地质, 2014, 41(6): 44−50.

ZHANG Jun, CHEN Zhengzhou, LIU Dengfeng. Stability evaluation of a rock slope based on the cloud model[J]. Hydrogeology and Engineering Geology, 2014, 41(6): 44−50.

[9] 苏永华, 何满潮, 孙晓明. 岩体模糊分类中隶属函数的等效性[J]. 北京科技大学学报, 2007, 29(7): 670−675.

SU Yonghua, HE Manchao, SUN Xiaoming. Equivalent characteristics of membership function type in rock mass fuzzy classification[J]. Journal of University of Science and Technology Beijing. 2007, 29(7): 670−675.

[10] 杨风暴, 王肖霞. D-S证据理论的冲突证据合成方法[M]. 北京: 国防工业出版社, 2010: 16−17.

YANG Fengbao, WANG Xiaoxia. Combination method of conflictive evidences in D-S evidence theory[M]. Beijing: National Defense Industry Press, 2010: 16−17.

[11] 刘海燕, 赵宗贵, 刘熹. D-S证据理论中冲突证据的合成方法[J]. 电子科技大学学报, 2008, 37(5): 701−704.

LIU Haiyan, ZHAO Zonggui, LIU Xi. Combination of conflict evidences in D-S theory[J]. Journal of University of Electronic Science and Technology of China, 2008, 37(5): 701−704.

[12] LI D, HAN J, SHI X, et al. Knowledge representation and discovery based on linguistic atoms[J]. Knowledge-Based Systems, 1998, 10(7): 431−440.

[13] 李德毅, 杜鹢. 不确定性人工智能[M]. 2版. 北京: 国防工业出版社, 2014: 44−55.

LI Deyi, DU Yi. Artificial intelligence with uncertainty [M]. 2nd ed. Beijing: National Defence Industry Press, 2014: 44−55.

[14] LI D, LIU C, GAN W. A new cognitive model: Cloud model[J]. International Journal of Intelligent Systems, 2009, 24(3): 357−375.

[15] YU Chao, YU Tao, HAI Su, et al. A method for trust management in cloud computing: Data coloring by cloud watermarking[J] International Journal of Automation and Computing, 2011, 8(3): 280−285.

[16] ZHOU K P, LIN Y, DENG H W, et al. Prediction of rock burst classification using cloud model with entropy weight[J]. Transactions of Nonferrous Metals Society of China, 2016, 26(7):1995−2002.

[17] 李德毅, 孟海军. 隶属云和隶属云发生器[J]. 计算机研究与发展, 1995(6): 15−20.

LI Deyi, MENG Haijun. Membership clouds and membership cloud generators[J]. Journal of Computer Research and Development, 1995, 32(6): 15−20.

[18] 徐飞, 徐卫亚, 刘造保, 等. 基于PSO−PP的边坡稳定性评价[J]. 岩土工程学报, 2011, 33(11): 1708−1713.

XU Fei, XU Weiya, LIU Zaobao, et al. Slope stability evaluation based on PSO−PP[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(11): 1708−1713.

[19] 黄奇, 费钒, 徐峰, 等. 基于物元模型的岩质边坡稳定性评估研究[J]. 地下空间与工程学报, 2012, 8(2): 439− 444.

HUANG Qi, FEI Fan, XU Feng, et al. Assessment research on the stability of rock-mass slopes based on matter-element model[J]. Chinese Journal of Underground Space & Engineering, 2012, 8(2): 439−444.

Application of finite cloud model and distance discrimination in slope stability evaluation

DAI Xingguo, ZHANG Biao, YAN Zezheng

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

Evaluation of slope stability is a comprehensive system problem with uncertainties, as characteristics index distributions and their classification boundaries are of fuzzy, this paper proposed a method to classify the stability of slope by using the cloud model with finite interval as the evaluation subject and the distance discriminant weighting. Calculation model and concept of finite cloud model and specific principles and processes of weighting were first discussed.And the evaluation index system of related literature was cited, the basic probability assignment of each index was calculated by the membership function and their weights were obtained based on indexes distance in the end. The cloud of each index on different stability levels was generated based on the cloud digital characters of evaluation indexes, and considering the measured evaluation index values and the corresponding weights, the comprehensive degrees of certainty were obtained. The slope stability level was identified by the maximum subordination principle.The results from case study and comparing with other theory methods show that the model proposed is feasible and effective, it can improve the shortcomings of inability to discuss quantitatively certainty and uncertainty relationships among indicators of interval distribution form from a unit way, so as to improve the universality for the cloud model application.

slope stability; distance discrimination; membership function; basic probability assignment; finite cloud model; comprehensive certainty degree

TP18

A

1672 − 7029(2018)01 − 0071 − 08

2016−12−07

戴兴国(1968−)，男，江西吉安人，教授，从事矿业系统工程、岩土力学方面的研究；E−mail：641251195@qq.com