概念层次架构的挖掘关联规则及其实证应用

, ,

(福建工程学院 管理学院, 福建 福州 350118)

关联规则是数据挖掘中主要的技术之一，其所挖掘的频繁项集主要是以1994年的Agrawal等人所提出的Apriori算法最具代表性[1]。然而Apriori算法在执行时会产生庞大数量的候选项目集合以及多次重复扫描数据库等缺点，进而造成算法效能不佳。因此许多学者都提出了许多改进的方式，其目的主要是减少数据库的扫描与增加执行上的效率。例如DHP算法可减少候选项目集，来生成关联规则[2]；DIC算法可同时扫描多个阶段，并降低扫描数据库的次数，提高整体效率[3]；FP-Growth算法是利用FP-tree的树状结构来将事务数据压缩在内，且在整个挖掘的过程中，只须扫描数据库两次。在过程中不须产生候选项目集，除了大幅的加快挖掘的速度外，还可节省大量的储存空间，因而整体的效率相当不错[4]。

其次，对于一个决策问题而言，需要考虑到使用者的认知与主观判断所产生的认知不确定性。Zadeh所提出的模糊理论可用来处理包含含糊性与意义不明确的认知不确定性[5]。再加上语意变数与语意值[6-8]所描述的模糊概念较符合决策者在主观上的认知，有助于决策分析的进行，因此近来的模糊数据挖掘则成为一项重要议题。

一般在对交易项目描述时，除了可用实体名称来表示外，交易项目之间还能透过抽象化的阶层方式来进行分类。也就是说，从较高阶层上来寻找项目间的关联性是个重要的研究。Han与Fu提出类似图1关于“食品”的树状结构的概念阶层结构图[9]，该结构模型有4个递阶层次，阶层编号由最上层开始编为层次0，直到产品最底层为层次3，而阶层越高名称越是广泛化(General)。例如在层次1的”Bread”在层次2里具有”White”与”Wheat”的广泛化概念。此外，由根节点到最低层次的某一节点则形成一条具有父子关系的路径。例如”Black tea”是”Beverage”的继承者，而”Linton”是”Black tea”的继承者。

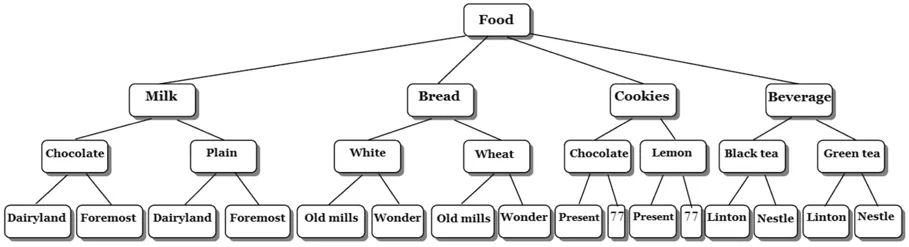
图1 关于“食品”的概念层次Fig.1 Conceptual hierarchy for “Food”

基于概念层次的挖掘，本文提出一项模糊数据挖掘方法。首先将架构的每个节点视为一个语意变量并以适当的数量来加以分割，接着采用FP-growth方式在多层次间挖掘模糊关联规则；并透过表格结构的方式来储存高频模糊格，这做法比传统交集方式更加快速，且在挖掘的过程中无需产生过多的候选项目集，即可完成整体挖掘任务。

1 相关文献研究

1.1 产生编码表

若一个阶层架构有h个层次，则每个节点能被编成h-1的序列。当一个节点编在层次j时，则节点将被转换成c1c2…cj-1cj…*，其j≤h-1且*的数量为h-j-1。其次，cu(u=1,2,…,j)为一个整数时，其值会由父节点的分支点来决定。以图1为例，阶层为4，故h= 4且节点的序列长为3。而“Bread”与“Plain”分别为根节点与“Milk”的第2个分支，因此“Bread”与“Plain”可被编成“2**”与“12*”。因此，通过此方法来进行编码后的结果如表1-表3所示。

表1 在阶层3所进行的编码转换Tab.1 Transcoding on Level 3

表2 在阶层2所进行的编码转换Tab.2 Transcoding on Level 2

表3 在阶层1所进行的编码转换Tab.3 Transcoding on Level 1

1.2 模糊切割法

语意变量的概念是由Zadeh所提出[5]，而一个语意变量的值可由自然语言的形式来表达[6-8]。因此，模糊分割系就是把每个语意变数以其所给予的语意值加以切割。例如{Small, Medium, Large}是一个定义在数量上的语意值集合。如图2所示，在2个二维空间上分别在x1与x2上定义了3个语意值，因此共有9个模糊格产生，其中的灰色阴影区则是所对应到的模糊格(A11,A23)。图2亦为使用模糊切割后的结果。

(1)

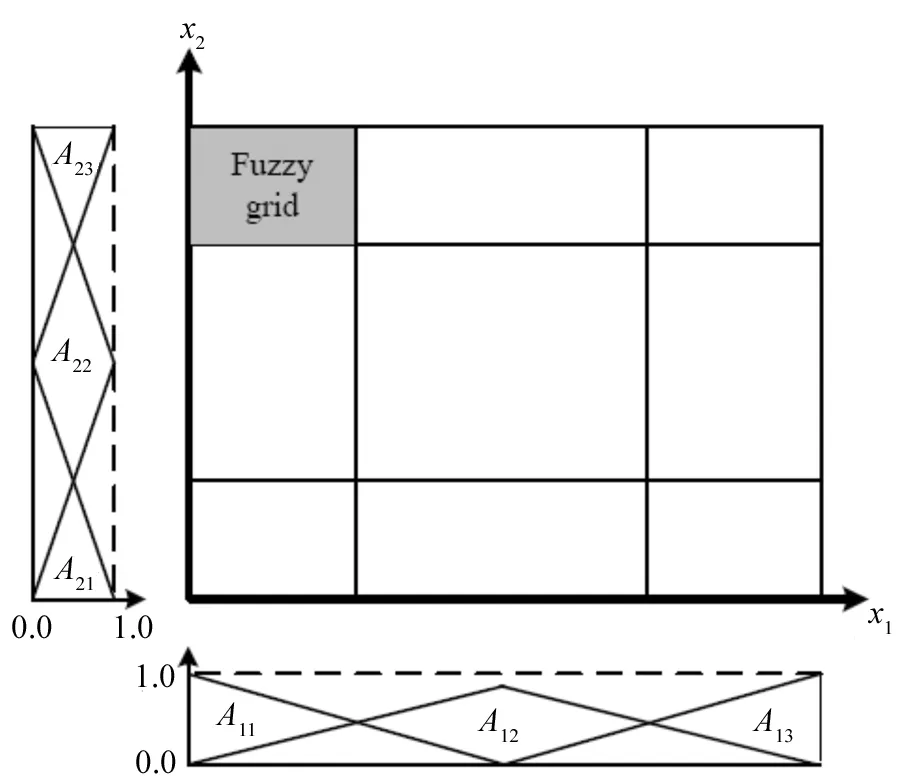
图2 关于x1与x2的模糊分割法Fig.2 Fuzzy partitions for x1 and x2

2 算法的提出及其原理步骤

首先简要介绍算法所使用到的符号表示。而表4是用来说明使用算法的交易事务数据集。图3则是此例用到的隶属函数。

2.1 符号表示

n: 交易事务数据的数量；

m: 使用来描述每一笔交易事务项的数量，其中1≤m；

xk: 第k个项，其中1≤k≤m；

K: 语意值在交易数据库里的每个量化项的语意值，其中K≥2；

tp: 第p笔的交易数据，其中1≤p≤n；

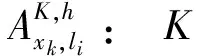
α: 预先指定的最小模糊支持度值；

β: 预先指定的最小模糊信赖度值；

h: 概念阶层的总层次，其中h≥ 1；

图3 此例所用到的量化隶属函数Fig.3 Quantization membership function used in this example

2.2 算法的提出

输入值：

(1)n笔的交易事务数据；

(2)每个语意变数有着K个语意值；

(3)概念层次的总层次；

(4)预先指定的最小模糊支持度值，α。

(5)预先指定的最小模糊信赖度值，β。

输出值：

模糊关联规则集。

步骤1：概念层次编码。概念层次有h层，则每个节点则被编成h-1个序列。如果编码的类型相同，数量则被合并。在表4的范例里以层次3进行处理，其结果如表1所示。

步骤3：建构表格FGTTFS并以由下步骤来生成高频模糊格。其范例格式如表6所示。

(1)模糊格(Fuzzy grid, FG)：每列表示一个模糊格与每行表示着语意值。

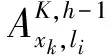
表4此例所使用的交易事务数据集
Tab.4Transactiondatasetusedinthisexample

TIDItems1(Milk⁃Chocolate⁃Dairland，5)，(Bread⁃White⁃Oldmills，5)，(Bread⁃White⁃Wonder，7)，(Bread⁃Wheat⁃Oldmills，2)，(Cookies⁃Chocoate⁃Present，9)，(Beverage⁃Greentea⁃Nestle，8)2(Milk⁃Chocolate⁃Dairland，5)，(Milk⁃Plain⁃Dairland，6)，(Milk⁃Plain⁃Foremost，3)，(Bread⁃Wheat⁃Wonder，7)，(Cookies⁃Lemon⁃Present，10)，(Cookies⁃Lemon⁃77，3)3(Bread⁃White⁃Wonder，7)，(Bread⁃Wheat⁃Wonder，3)，(Cookies⁃Chocolate⁃Present，5)，(Cookies⁃Lemon⁃77，6)4(Milk⁃Chocolate⁃Dairland，6)，(Milk⁃Chcoclate⁃Foremost，1)，(Bread⁃White⁃Oldmills，5)，(Bread⁃White⁃Wonder，6)，(Cookies⁃Chocolate⁃Present，7)，(Cookies⁃Lemon⁃Present，3)，(Beverage⁃Blacktea⁃Nestle，3)，(Beverage⁃Greentea⁃Linton，1)5(Milk⁃Chcoclate⁃Dairland，3)，(Milk⁃Chocolate⁃Foremost，10)，(Bread⁃White⁃Oldmills，2)，(Bread⁃Wheat⁃Wonder，4)，(Beverage⁃Blacktea⁃Linton，3)，(Beverage⁃Blacktea⁃Nestle，9)

表5 将交易事务数据集转换成模糊集

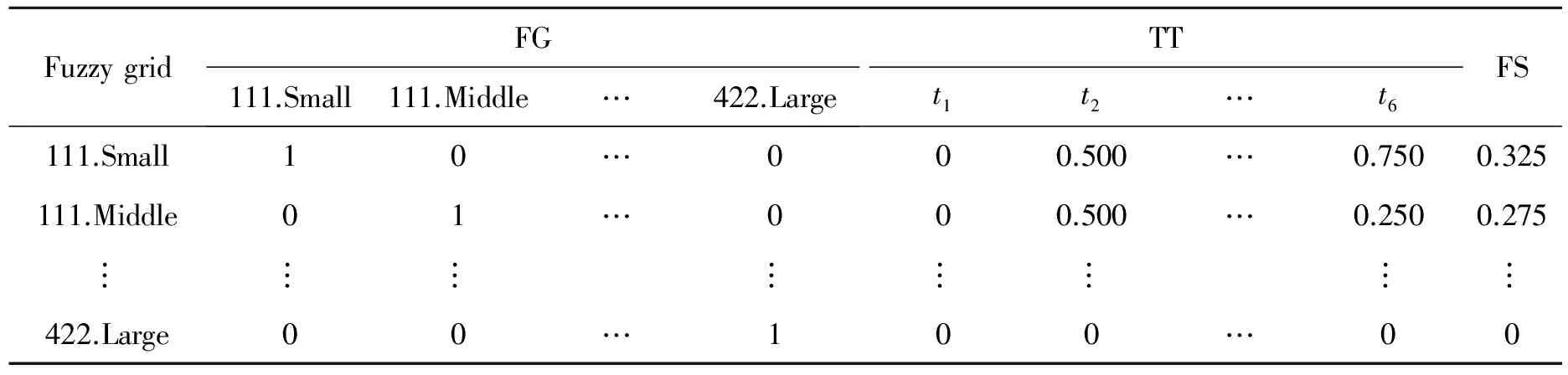
表6 建构于阶层3的表格FGTTFSTab.6 Table FGTTFS for items on Level 3

(3)模糊支持度(Fuzzy support, FS)：其存放所对应模糊格的模糊支持度，其计算方式为下式。

(2)

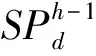
Small、211.Small、212.Middle、222.Small与311.Middle等6个1维高频模糊格。

步骤7：计算每个1维高频模糊格值的总和并构建一个递减名为Header Table的表格，如表7所示。接着就进行模糊FP-growth。

表7 阶层3的Tab.7 Header table of Level 3

步骤8：在扫描模糊集时首先要重新建构模糊集表，如图4所示，其模糊集是按照Header Table来排序。

表8 阶层3的新模糊集Tab.8 New fuzzy sets of Level 3

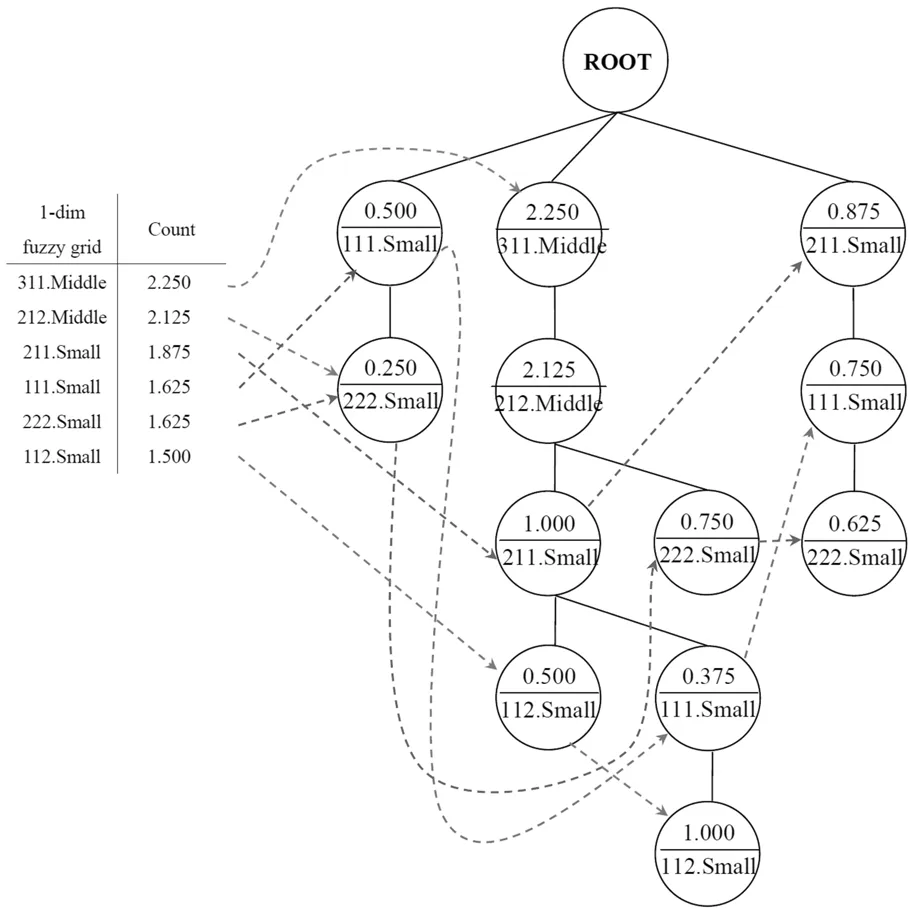
图4 阶层3的模糊FP-treeFig.4 Fuzzy FP-tree of Level 3

步骤9：在模糊FP-tree(FFP-tree)的根节点上设置{ROOT}。在第2次扫描时新的模糊集就能在树里的模糊格基于相同的交易事务来连接节点，以建构出模糊FP-tree。其结果如图4所示。

步骤10：在模糊FP-tree里挖掘可能的高频样式。从Header Table最底端开始扫描并从中取得模糊FP-tree从每个项所建构的路径里的条件式模式基底。其次，每个项的条件隶属函数FP-tree能由条件模式基础来建构起来。则每个项可能的全部集将从条件模糊FP-tree里生成出来。在此例子里，其结果如表9所示。

步骤11：使用下列步骤来找出所符合的高频样式。

(1)把所生成的高频样式放入表格FGTTFS计算其模糊支持度，其结果如表10所示。

(2)检查每个高频样式的模糊支持度是否大于或等于预先指定的最小模糊支持度值。

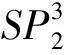
表9 阶层3所生成的所有可能样式Tab.9 All possible generated patterns of Level 3

表10 阶层3的所有路径的表格FGTTFSTab.10 Table FGTTFS for all paths on Level 3

(3)

在此范例里，候选关联规则是:

212.Middle→311.Middle；311.Middle→212.Middle；

21*.Middle→31*.Middle；31*.Middle→21*.Middle；

2**.Middle→3**.Middle；3**.Middle→2**.Middle。

它们的模糊信赖度值分别为0.750, 0.708, 0.694, 0.694, 0.611与0.660。

(1)若Bread White Wonder的购买量为中等量时，则Cookies Chocolate Present的购买量为中等量。

(2)若Cookies Chocolate Present的购买量为中等量时，则Bread White Wonder的购买量为中等量。

(3)若Bread White的购买量为中等量时，则Cookies Chocolate的购买量为中等量。

(4)若Cookies Chocolate的购买量为中等量时，则Bread White的购买量为中等量。

(5)若Cookies的购买量为中等量时，则Bread的购买量为中等量。

3 算例实验及其结果分析

本实验就所提出的方法在不同的数据库大小(包含随机产生的10 000与20 000笔交易事务)与最小模糊支持度的设定下来探讨运行时间与关联规则的生成所造成的影响。算法是以C#.Net设计，并在配备为3.07GHz的Intel Core i3的个人计算机上执行，其使用Windows Server 2003 R2的作业系统与SQL Server 2008的数据库上执行。所使用的概念阶层如图1所定义，而在每笔交易事务中，所购买的项及其数量由随机产生，但购买数量不超过17单位，且购买项不会重复产生。所使用的模糊集如图3所示。

将最小模糊支持度设为0的情况下，所得到的结果如表11与表12所示。在表11与表12的实验结果则包含了Hong等的方法[10]与Hu的方法[11]得到的数据来比较。从中能发现到最小模糊支持度设定得越小，所产生的关联规则就越多。在运行时间上，所提的方法明显优于Hang等与Hu的方法，尤其当最小模糊支持度越小就越明显。这也显示出本文所提出的方法在使用FP-growth与运用表格FGTTFS于阶层架构下来产生高频模糊格及关联规则下，可有效的提升整体的执行效率。且较小的最小模糊支持度也不会严重影响到所提出方法的运行时间。

另外，在关联规则的产出数量上，Hong等方法的特点是选取了每一个量化属性上最大模糊支持度的一维模糊格；而Hu的方法特点则是考虑所有的高频一维模糊格。至于本文所提出的方法，把上述两项特点结合，进而使所产生的高频模糊格数量能在每一量化属性上有着最大的模糊支持度并能把所有的高频一维模糊格作整体的挖掘。因此，能获得较优的效能。

表11 10 000笔交易的实验结果Tab.11 Experimehtal results of 10 000 transactions

表12 20 000笔交易的实验结果Tab.12 Experimental results of 20 000 transactions

4 结论

本文应用模糊分割法与FP-Growth算法的手段，提出一种在阶层概念里来找寻模糊关联规则的方法，该方法使用编码方式将阶层里的项逐一编码，然后使用模糊分割法来找出1维模糊格，再使用FP-Growth算法，在各阶层找寻可生成的模糊关联规则。最后，通过与Hong等及Hu的方法进行比较，验证本方法的有效性，由于FP-Growth之特性在于不用产生候选项集、且将数据库给压缩在FP-tree中，故本文的方法有着较佳的执行效率。

其次，在语意值的设定上，使用者可依据本身的偏好、过去的使用经验来主观设定语意值个数及其形状，如高斯分布或梯形隶属函数，如此能更符合使用者在主观上的认知。且Pedrycz也提到在模糊系统上使用三角形隶属函数是具有实用性及有效性[12]，故本研究采用三角隶属函数作为模糊计算的隶属度函数。

本研究不足之处是实行时忽略了语意值个数与交易事务记录笔数会影响到FGTTFS表格的使用空间。当语意值个数越大时，FG则需要越多的使用空间；当交易事务记录笔数越多时，TT所设定的使用空间就越大。若能节省FGTTFS的使用空间，势必能让算法的效能更加提升。至于在未来的研究展望上，对于设定使用者所给定的参数上，遗传算法(Genetic algorithm)可考虑作为自动决定适合参数的工具，这是由于遗传算法具有自动搜寻的特性。至于最小模糊支持度以及在每个量化属性上所设定的个数K，Hong等[13]建议可透过遗传算法的方式来自动取得。而这些建议也是未来继续使用数据挖掘的方法来解决各类型问题的重要参考。

[1] Agrawal R, Srikant R. Fast algorithm for mining association rules in large database[C]∥. Proceeding of 20th International Conference on Very Large Databases. Santiago:[s.n.],1994:478-499.

[2] Park J S, Chen M S, Yu P S. An effective hash based algorithm for mining association rules[C]∥. Proceeding of the 1995 ACM SIGMOD International Conference on Management of Data. San Jose: ACM Press,1995:175-186.

[3] Brin S,Motwani R, Ullman J D, et al. Dynamic itemset counting and implication rules for market basket data[C]∥. ACM SIGMOD International Conference on Management of Data. New York: ACM Press,1997:255-264.

[4] Han J, Pei J, Yin Y. Mining frequent patterns without candidate generation[C]∥. Proceeding 2000 ACM SIGMOD International Conference Management of Data. Dallas: ACM Press,2000:1-12.

[5] Zadeh L A. Fuzzy sets[J].Information and Control,1965,8(3):338-353.

[6] Zadeh L A. The concept of a linguistic variable and its application to approximate reasoning-Ⅰ[J].Information and Science,1975,8(3):199-249.

[7] Zadeh L A. The concept of a linguistic variable and its application to approximate reasoning-Ⅱ[J].Information and Science,1975,8(4):301-357.

[8] Zadeh L A. The concept of a linguistic variable and its application to approximate reasoning Ⅲ[J].Information and Science,1976,9(1):43-80.

[9] Han J W, Fu Y J. Discovery of multiple-level association rules from large database [C]. In Proceedings of International Conference on Very Large Data Bases. Zurich, 1995: 420-431.

[10] Hong T P， Lin K Y, Chien B C. Mining fuzzy multiple-level association rules from quantitative data[J].Applied Intelligence,2003,18(1):79-90.

[11] Hu Y C. Mining association rules at a concept hierarchy using fuzzy partition [J]. Journal of Information Management,2006,13(3):63-80.

[12] Pedrycz W. Triangular membership functions[J].Fuzzy Sets and Systems,1994,64(1):21-30.

[13] Hong T P, Chen C H, Lee Y C, et al. Genetic-fuzzy data mining with divide-and-conquer strategy[J].IEEE Transactions on Evolutionary Computation,2008,12(2):252-265.