基于主成分分析的纤维拉伸断裂声发射信号识别

张陆佳， 林兰天， 陈春敏， 申炎仃， 高 琮

(上海工程技术大学 服装学院， 上海 201620)

纱线强力受到纤维性能以及纱线结构等因素的影响，有学者通过构建力学模型改变纱线结构提高强力利用率[1]。纤维性能是影响纱线强力利用率的指标之一，相关研究大都集中在从力学角度进行分析，常采用拉伸断裂强力、断裂伸长率等表征指标。对于混纺纱，不同材料纤维的结构特征各不相同，仅靠力学性能指标较难科学全面地揭示纤维断裂的过程，进而有效地提高纱线的强力利用率[2]。

本文以纤维拉伸断裂声发射信号的检测为切入点，通过增强经验模态分解(EEMD)的信号处理方法获取纤维拉伸断裂信号特征，在此基础上提出主成分分析(PCA)并结合最小二乘支持向量机(LSSVM)识别的模型(即EEMD-PCA-LSSVM模型)，实现对纤维拉伸断裂声发射信号特征向量的重组及降维，探索可适用于不同种类纤维拉伸断裂信号特征及识别的方法，为深入研究混纺纱线拉伸断裂过程中多种纤维断裂的时序性提供依据。并以此分析各组分纤维的拉伸强力贡献程度，从而精准优化调整纺纱工艺的设计与生产。

1 EEMD-PCA-LSSVM模型的建立

1.1 声发射信号预处理

声发射(简称AE)是材料局部因能量的快速释放而发出的瞬态弹性波的现象[3]。声发射传感器获得的信号较大部分是由噪声产生的，在放大器的作用下，噪声信号使得A/D转换器处于满量程状态而被存储到计算机中[4]。

纤维拉伸断裂AE信号强度一般比较弱，且会受到传输通道、换能器等硬件因素的影响，使得最终采集的AE信号较为复杂；同时，纤维拉伸断裂信号采集是一个动态检测的过程，信号的实时性难以保证：因此，需对纤维拉伸断裂AE信号进行去噪。

针对纤维拉伸断裂AE信号特点，采用小波去噪。以涤纶纤维为例，纤维拉伸断裂为瞬时的能量释放，其声发射信号表现为脉冲波形的突变，脉冲峰值大，衰减快，即断裂信号为一个极其突出的针尖状信号，在极短的时间内出现较大的幅值变化；因此，对涤纶单纤维拉伸断裂AE信号小波去噪，其中小波基为sym 6函数，分解层数为5，去噪结果如图1所示。

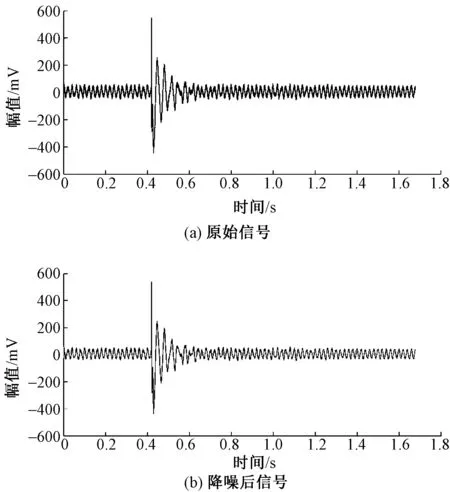
图1 涤纶纤维拉伸断裂AE信号小波去噪前后对比图Fig.1 AE signal of tensile fracture of polyester fiber before (a)and after (b) treated by wavelet analysis

经小波去噪后，纤维拉伸断裂声发射信号中噪声杂刺明显减少，曲线平滑，小波去噪有效果。为了减少后续分析工作，根据统计结果对断裂信号进行有效部分的截取，如图2所示。

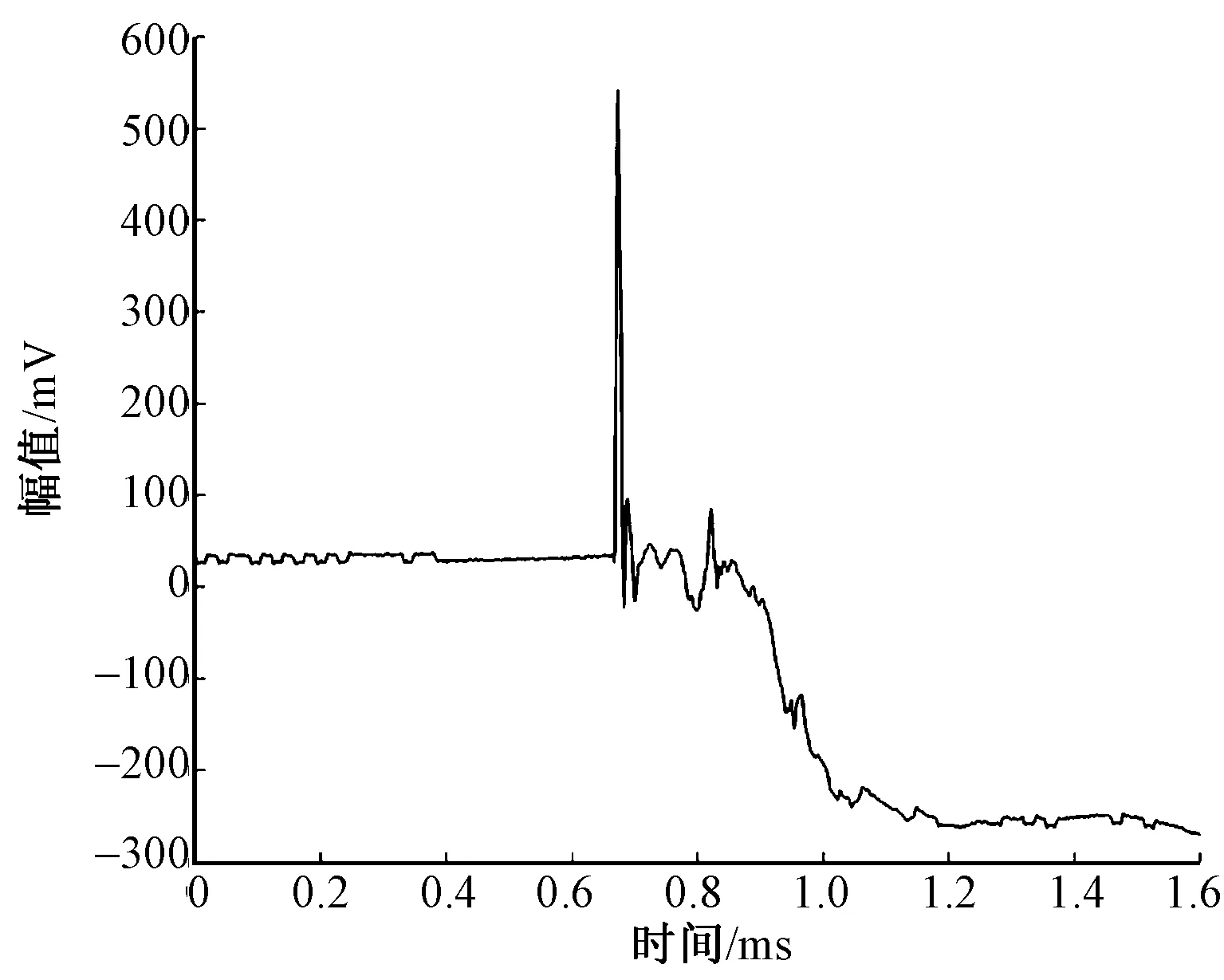
图2 涤纶纤维AE信号有效部分截取图Fig.2 Signal of polyester fiber fracture zone

1.2 模型建立

在对比不同种类纤维的拉伸断裂AE信号时发现在时域内其特征不明显，往往振动信号特征多从频域内进行提取，一般将信号分解为多个分量，并计算每个分量的特征值，以提取原始信号的特征；因此，针对纤维拉伸断裂AE信号的特点建立EEMD-PCA-LSSVM模型，实现对不同纤维种类断裂的分类识别。该模型由3部分组成：1)利用增强经验模态分解方法对AE信号进行分解，获取纤维的频率特征；2)利用主成分分析法对高维的频率特征集进行提取，实现特征降维，获得频率的训练特征集、识别特征集；3)通过LSSVM分类器的训练实现对纤维断裂信号的识别。其建模的流程如图3所示。

1.2.1增强经验模态分解方法

在实际生产和生活中，大多数信号均具有非线性、非平稳性；同时为避免经验模态分解(EMD)在分解含噪声的信号时出现模态混叠现象，表现为相邻2个固有模式函数(Intrinsic mode function，简称IMF)波形混叠不易分辨[5]：因此，在分解纤维拉伸断裂AE信号时，采用增强经验模态分解(简称EEMD)作为信号的时频分解方法。该方法利用不同白噪声序列与对应的IMF之间存在不相关性，在信号中添加白噪声，使得干扰脉冲在EMD分解过程得到消除，解决经验模态分解中的模态混叠问题[6]。

EEMD分解得到较多IMF分量；但仅有少量的IMF对应有效的信号，因此，与原始信号相关系数高的分量可视为含原始信号的有效成分较多，选取相关程度高的IMF进行后续分析。

图3 纤维拉伸断裂AE信号预处理、EEMD-PCA-LSSVM模型流程图Fig.3 Flowchart of fiber tensile fracture AE signal pretreatment and EEMD-PCA-LSSVM model

图4 纤维断裂区信号的EEMD分解图Fig.4 EEMD decomposition on signal of fiber fracture zone

以涤纶纤维的1个样本为例，对去噪后的纤维信号采用EEMD方法分解处理，其中设白噪声幅值系数为0.01，执行循环次数为50。图4为纤维断裂信号的EEMD分解图。可以看出，涤纶纤维的AE信号经分解得到12个IMF分量，其中IMF1到IMF12依次由高频段至低频段变化。由于纤维断裂频率的分布属于高频段，且前12个IMF与原始信号的相关系数R(i)如表1所示。因此，阈值为相关序列值R(i)>5%时，对应选择前10个IMF分量作为有效的IMF分量，记作IMF-10 ={IMF1，IMF2，…，IMF10}。

对IMF-10进行希尔伯特变换得到希尔伯特谱和边际谱，如图5、6所示。边际谱的幅值可以描述信号的幅值在整个频率段上随频率的实际变化情况，通过该涤纶纤维的边际谱可知在整个频率段0～5 MHz范围出现多个幅值较大的特征峰，选择边际谱中波峰出现的频率段作为该试样的特征频率集。表2示出10个维纶纤维样本的特征频率集。

表112阶IMF分量与原始信号的相关系数表
Tab.1Phaserelationtableof12-stepIMFcomponentwithoriginalsignal

IMF分量相关系数R(i)IMF分量相关系数R(i)IMF10.104IMF70.142IMF20.095IMF80.295IMF30.111IMF9-0.205IMF40.110IMF100.799IMF50.103IMF11-0.028IMF60.097IMF12-0.013

图5 希尔伯特谱Fig.5 Hilbert spectrum

图6 边际谱Fig.6 Marginal spectrum

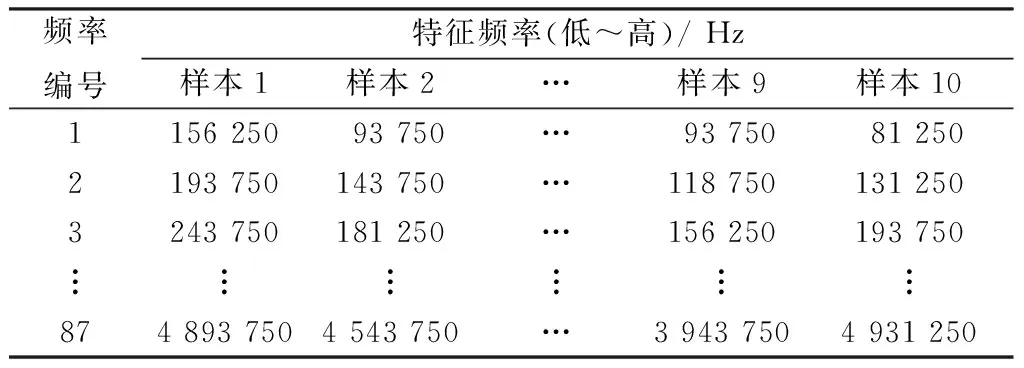
频率编号特征频率(低～高)/Hz样本1样本2…样本9样本10115625093750…93750812502193750143750…1187501312503243750181250…156250193750︙︙︙︙︙︙8748937504543750…39437504931250

1.2.2主成分分析

涤纶纤维拉伸断裂AE信号经EEMD处理后获取的频率特征的维度较大，特征的差异较小，如图7所示。涤纶纤维特征频率间相关系数的绝对值越大，颜色越深。21.69%的频率特征间的相关系数小于0.4，即这部分数据间弱相关；而63.06%的频率特征间相关系数大于0.6，即这部分数据强相关,说明数据信息大量重叠：因此，不能直接将频率特征作为模式识别分类的最佳特征，需要对特征向量重组，舍弃无用或信息重叠的频率特征。

图7 频率特征相关系数图Fig.7 Correlation coefficient of characteristics frequency chart

主成分分析法(PCA)可将多维特征压缩成较少维数[7]。Malhi等[8]利用PCA从多域特征中提取2个有效特征，实现对轴承故障的分类。任浩等[9]提出基于PCA的多级支持向量机情感分类算法，使特征维度降低58.3%，并逐级对输入语音所属的情感类型进行判断，相比基于支持向量机其平均识别率提高5.05%。

针对涤纶纤维频率特征集的特征反映的特点，可对纤维的特征频率采用主成分分析法进行提取。涤纶纤维AE信号87维频率特征经PCA处理后得到2个主成分，其累积贡献率为86.813%。提取对这2个主成分贡献率大的频率作为涤纶纤维新的特征频率集，减少噪声等其他干扰成分，突出有用的信息特征。

1.2.3支持向量机

最小二乘支持向量机(LSSVM)是Suyken等[10]基于支持向量机方法的改进，其与支持向量机模型相比能够将不等式的约束改为等式约束，能够将求解二次规划问题转化为直接求解线性方程，规避了支持向量机的弊端[11]。

根据纤维材料种类个数，建立N个两类分类器LSSVM1、LSSVM2、……、LSSVMN，并通过训练样本对LSSVM分类器进行训练。在识别过程中，识别样本依次经过分类器，当LSSVM1分类器输出为1，分类结束；反之，当SVM1分类器输出为0，便会自动将特征向量输入到下一个分类器。所构建的分类器如图8所示，x=(x1,x2,…,xn)为输入向量，即n个待训练样本；K(Xi,X)为基于支持向量机的非线性变换，即核函数，其中i=(1，2，…，N)，Xi为训练样本，X为待分类样本；yiαi为权值，其中yi表示相应类的标识器，αi表示Lagrange乘子。

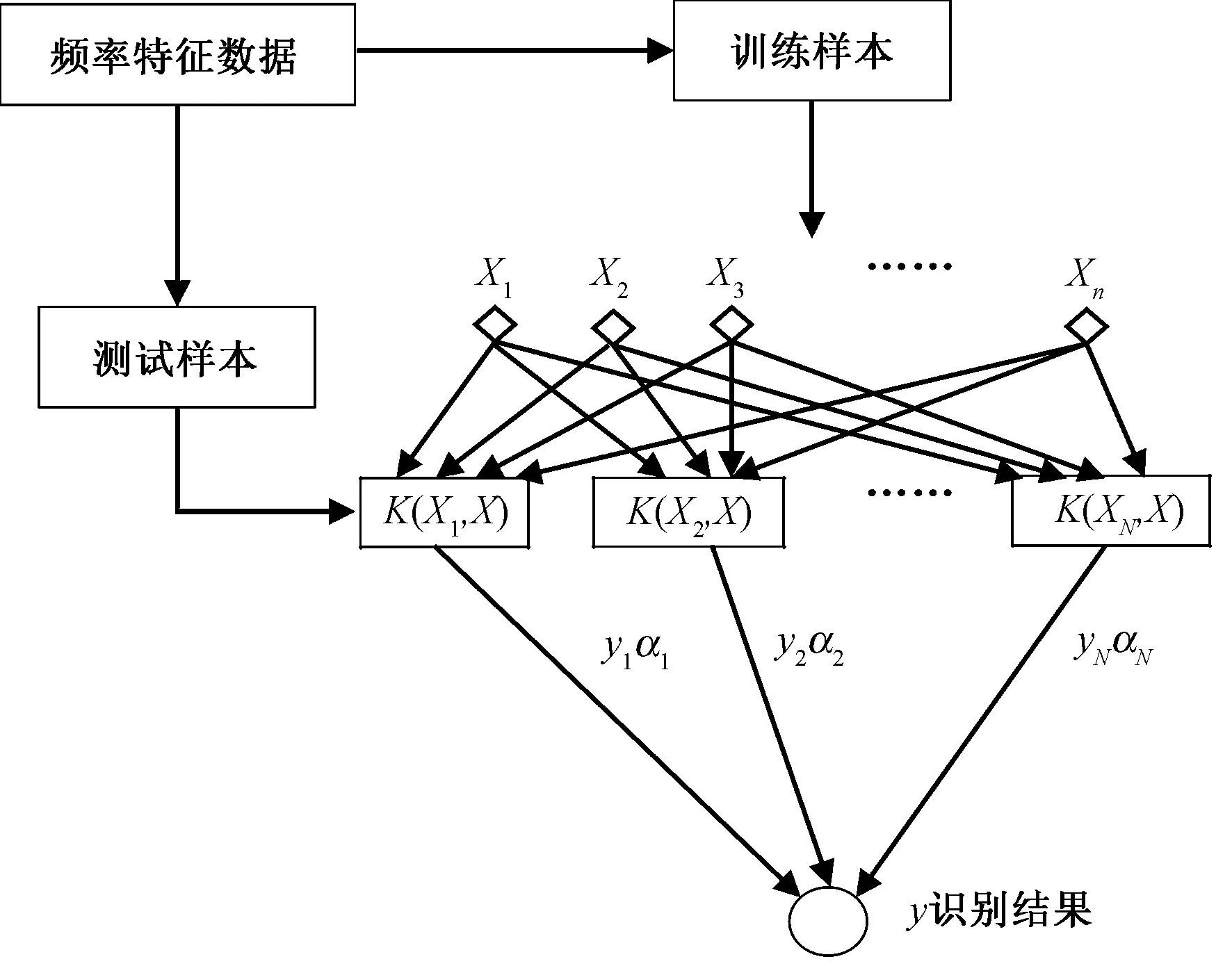
图8 支持向量机结构图(纤维拉伸断裂AE信号)Fig.8 Structure diagram of support vector machine (fiber tensile fracture AE signal)

2 实验与分析

纤维拉伸断裂声发射信号是在采集平台上获取的，鉴于样本的宽度要求，该平台由YG065C型电子织物强力仪、PVDF压电传感器、数据采集仪和计算机构成。强力仪选择定速拉伸，拉伸速度为250 mm/min，拉伸隔距为70 mm。数据采集卡触发电压为10 mV，采样频率为10 MHz。实验材料选用1.67 dtex芳纶1313、1.55 dtex高性能维纶，其断裂强力的平均值分别为7.8、11.5 cN。将芳纶1313、高性能维纶分别制成单纤维样本，在织物强力机上进行拉伸测试，分别进行100次实验。

根据构建的EEMD-PCA-LSSVM模型，分别对芳纶1313和高性能维纶纤维的100个样本(芳纶1313为n1-i，高性能维纶纤维为n2-i；i=1,2,…，100)的拉伸断裂AE信号进行预处理，并完成断裂区间的截取。对截取的2种纤维材料的AE信号结果进行EEMD分解，利用芳纶1313和维纶各100个样本的边际谱进行特征频率选取，可得到频率特征分别为X100×80和Y100×70。

表3、4分别示出2种纤维材料的频率特征经PCA处理的结果。芳纶1313的频率特征X和高性能维纶的频率特征Y的前2个主成分的累计方差贡献率已经分别达到87.210%和 86.880%，即前2个主成分已经包含了原信息85%以上的信息量。针对原特征频率的2个主成分的频率特征矩阵，在保证维度一致的前提下提取与第1主成分、第2主成分相关系数较高的频率作为芳纶1313、高性能维纶新的频率特征，即分别为(X0)100×36、(Y0)100×36，实现了对2种纤维特征频率的降维，且特征之间相互独立。

表3 芳纶1313特征主成分累计贡献率Tab.3 Contribution rate of characteristic frequency of poly-1,3-phenylene isophthalamide

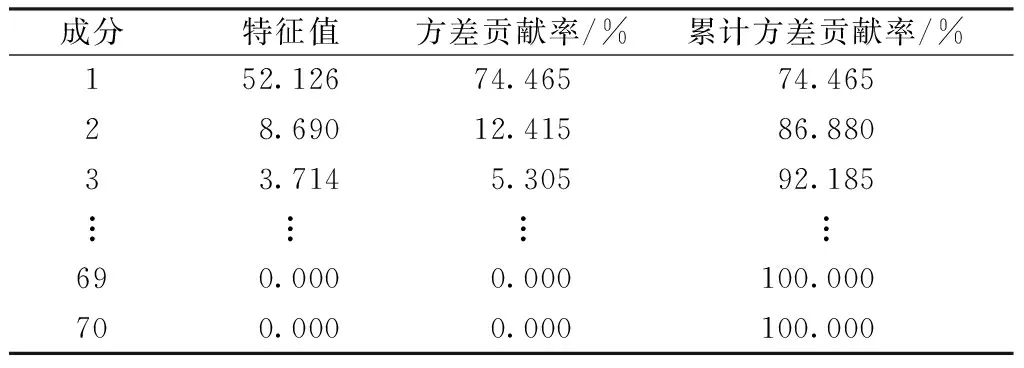
表4 高性能维纶特征主成分累计贡献率Tab.4 Contribution rate of characteristic frequency of high performance vinylon

对经PCA处理过后的2种纤维的特征频率X0、Y0进行归一化处理，并令其中样品n1-1～n1-50、样品n2-1～n2-50分别作为芳纶1313和高性能维纶的训练样本，样品n1-51～n1-100、样品n2-51～n2-100分别作为芳纶1313和高性能维纶的测试样本。通过建立支持向量机识别器对不同种类纤维断裂情况进行归类。按照纤维种类构建纤维拉伸断裂AE信号LSSVM识别器，即由2个LSSVM分类器构成，其中核函数选择径向基核函数，惩罚因子和核参数分别为2。诊断结果中，断裂样本用1表示，没有正确识别或者没有断裂用0表示，如表5所示。

从表5看出，该模型在对芳纶1313、高性能维纶纤维各50个样本的总识别率分别为96%，绝大部分测试样本的测试结果与实际相符，仅有高性能维纶纤维的4个样本未获识别。可见，构建的LSSVM分类器可较好地实现对不同品种纤维拉伸断裂特征频率的分类识别。EEMD-PCA-LSSVM模型可对纤维拉伸断裂声发射信号实现较高的识别，对纤维拉伸断裂机制研究以及纤维生产过程中工艺设计具有积极的意义。

表5 LSSVM分类结果Tab.5 Results of LSSVM classification

3 结 论

利用EEMD-PCA-LSSVM模型建立纤维拉伸断裂声发射信号的识别算法，其中在纤维拉伸断裂声发射信号处理过程中，对信号特征信息处理方法进行改进优化：通过PCA对特征向量进行选取和降维处理；利用训练LSSVM分类器实现对2种纤维分类准确识别。通过研究得出以下结论：

1)EEMD-PCA-LSSVM模型可对不同纤维断裂声发射信号进行预测分类，模型与信号特征向量之间可以建立映射关系。

2)利用主成分分析法对多维且具有较高相关性的纤维拉伸断裂声发射信号特征频率进行降维、同维处理，该方法可有效地降低特征的相关性，将其作为LSSVM识别模型训练及识别的输入特征，可有效地改善识别效果。

3)EEMD-PCA-LSSVM模型对芳纶1313、高性能维纶纤维拉伸断裂情况具有96%的识别率，也可对其他不同种类纤维拉伸断裂情况进行识别与表征。

[1] 黄伟, 汪军. 复合纱线结构对单纱强力利用率的影响与分析[J]. 纺织学报,2017,38(2): 99-105.

HUANG Wei, WANG Jun. Influence of composite yarn′s structures on yarn strength efficiency[J]. Journal of Textile Research, 2017, 38(2):99-105.

[2] 毋戈. 束纤维拉伸中的声与断裂力学的原位表征[D]. 上海:东华大学,2013:2-3.

WU Ge. Characterization in situ for acoustic emission and tensile mechanics of fiber bundle at breaking[D]. Shanghai: Donghua University, 2013:2-3.

[3] 许中林, 李国禄, 董天顺, 等. 声发射信号分析与处理方法研究进展[J]. 材料导报,2014,28(5): 56- 60, 73.

XU Zhonglin, LI Guolu, DONG Tianshun, et al. Advances of analysis and processing methods of acoustic emission signal[J]. Materials Review, 2014, 28(5): 56-60, 73.

[4] 李思辉. 声发射技术在防弹用复合材料检测上的应用[J]. 纺织科技进展,2007(2): 11- 12.

LI Sihui. The application of acoustic emission technique in testing bulletproof composites[J]. Progress in Textile Science & Technology, 2007(2):11-12.

[5] WU Z, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009(1):1-41.

[6] HUANG N E, WU Z. A review on Hilbert-Huang transform: method and its applications to geophysical studies[J]. Reviews of Geophysics, 2008, 46:26-30.

[7] 于成龙. 基于PCA的特征选择算法[J]. 计算机技术与发展,2011(4): 123-125.

YU Chenglong. Features selection algorithm based on PCA[J]. Computer Technology and Development, 2011(4):123-125.

[8] MALHI A, GAO R X. PCA-based feature selection scheme for machine defected classification[J]. IEEE Transactions on Instrumentation and Measurement, 2004, 53(6):1517-1525.

[9] YU Huanwei, XU Yanling, LV Na, et al. Arc spectral processing technique with its application to wire feed monitoring in Al-Mg alloy pulsed gas tungsten arc welding[J]. Journal of Materials Processing Technology, 2013, 213 (5):707-716.

[10] JAK S, VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293-300.

[11] 毛勇. 基于支持向量机的特征选择方法的研究与应用[D]. 杭州:浙江大学,2006:12-18.

MAO Yong. A study on feature selection algorithms based on support vector machine and its application[D]. Hangzhou: Zhejiang University, 2006:12-18.