广义半连续向量值函数与应用
廖怡娜,金朝永
(广东工业大学 应用数学学院,广东 广州 510520)
1 引言及预备知识
众所周知,函数的凸性和连续性在非线性优化中扮演着重要的角色. 比如:分离定理,极小极大定理和鞍点定理都与函数的凸性和连续性紧密相关. 在过去几十年里,向量优化也得到快速的发展(见,[1-6]).
本文目的是借助Chen[7][8]给出的广义半连续函数的概念和Finet[4]提出的序半连续向量值函数定义,利用半连续性得到向量值函数的Pareto 优化解和对广义鞍点定理进行推广,最后讨论了一类向量平衡问题的解的存在性问题.
这里假设N是正的自然数,E是实序Banach空间,C⊂E是闭凸尖锥且intC≠Ø,引入E上的序关系:y≤x⟺x-y∈C,∀x,y∈E. 若y 为叙述方便,我们给出如下定义: 定义1.1[7-8]是实Banach空间. (3)若f在X上上方下半连续是指在X中的每一点都是上方下半连续的;若f在X上下方上半连续是指在X中的每一点都是下方上半连续的. 注1.1 (a) 显然上方下半连续和下方上半连续是半连续函数的推广.反之,不成立. (b) 在文献[10]中上方下半连续和下方上半连续也被定义为单调半连续. 显然f在0处是上方下半连续,但不是下半连续. 下面我们介绍向量值映射上的半连续定义. 定义1.2[1,4,8,9]设X是实Banach空间,假设f∶X→E是一个向量值映射. (1) 若f在x0∈X是C-下半连续,是指对f(x0)的任意邻域V,都存在x0的一个邻域U,使得f(x)⊂V+C,∀x∈U. (2) 若f在x0∈X是C-拟下半连续,是指对任意的b∈E,{x∈X∶f(x)≤b}是闭集. (3) 若f在x0∈X是序下半连续,是指对每一个序列{xn}⊂E使得xn→x0,就存在序列{εn}⊂E收敛于0且f(xn)+εn≥f(xn+1)+εn+1,∀n∈N,则存在序列{gn}⊂E收敛于0使得f(x0)≤f(xn)+gn,∀n∈N. (4) 称f∶X→E在x0∈E是C-上方下半连续,如果对任意的序列{xn},xn→x0,f(xn+1)≤f(xn),∀n∈N使得f(x0)≤f(xn). 注1.2 (a)f是C-上半连续是指-f是C-下半连续,f是C-拟上半连续是指-f是C-拟下半连续,f是序上半连续是指-f是序下半连续,f是C-下方上半连续是指-f是C-上方下半连续. (b) 若E=R,很容易得到(1)(2)(3)是等价的,但对于无穷维空间就不成立了(见,[4]). 但是有(1)⟹(2)⟹(4),(1)⟹(3),由于假设intC≠Ø,从而(2)⟹(3). (c) 现在我们证明(3)⟹(4). 事实上,任取{xn}⊂X使得xn→x0且f(xn)≥f(xn+1),由于f是序下半连续,故存在序列{gn}收敛于0使得 f(x0)≤f(xn)+gn. 又因为对∀n,l∈N,f(xn+l)∈f(xn)-C,那么有 f(x0)∈f(xn+l)+gn+l-C⊂f(xn)-C+gn+l-C=f(xn)+gn+l-C. 因为C是闭的,所以f(x0)≤f(xn),∀n∈N. 所以(3)⟹(4). (d) 从注(c)可知C-上方下半连续比序下半连续更弱. 那么结合注(b)(c)可得 (1)⟹(2)⟹(3)⟹(4) 定理1.1设X是实Banach空间,若β∶X→(0,+∞)是上方下半连续,对每个v∈C,则F(x)=β(x)v是C-上方下半连续. 证明:任取{xn}⊂E使得xn→x0,F(xn)≥F(xn+1),可推出β(xn)≥β(xn+1). 因为β(x)是上方下半连续,故β(x0)≤β(xn). 因此对每个v∈C,则β(x0)v≤β(xn)v,∀n∈N. 注1.3 若β是下半连续函数,则β(x)v是C-下半连续的. 这相应的结果是[9]中定理2.1的结果. 更一般地,β(x)v是序下半连续. 定义1.3[2,3]设A⊂E非空子集. (1)称x∈A极小点,如果A∩(a-C)={a};记minA是A中所有极小点的集合. (2)称x∈A极大点,如果A∩(a+C)={a};记maxA是A中所有极大点的集合. (3)称x∈A弱极小点,如果A∩(a-intC)=Ø;记minwA是A中所有弱极小点的集合. (4)称x∈A弱极大点,如果A∩(a+intC)=Ø;记maxwA是A中所有弱极大点的集合. 显然,minA⊂minwA,maxA⊂maxwA. 定义1.4[3,9]设X和Y是实Banach空间,假设f∶X×Y→E是一个向量值映射. (1)称(x0,y0)∈X×Y是f的C-鞍点,是指 f(x0,y0)∈maxf(x0,Y)∩minf(X,y0). (2)称(x0,y0)∈X×Y是f的弱C-鞍点,是指 f(x0,y0)∈maxwf(x0,Y)∩minwf(X,y0). 注1.4 显然,f的C-鞍点都是弱C-鞍点. 定义1.5[2,3]设X0⊂X是非空凸子集,f∶X0→V是一个向量值映射. (1)称f在X0是C-凸,是指对任意x1,x2∈X0,∀t∈[0,1]有 f tx1+(1-t)x2 ≤tf(x1)+(1-t)f(x2). (2)称f在X0是真C-拟凸,是指对任意x1,x2∈X0,∀t∈[0,1]有 f tx1+(1-t)x2 ≤f(x1)或f tx1+(1-t)x2 ≤f(x2) 至少有一个成立. 注1.5 若-f在X0是C-凸,则称f是C-凹.;若-f在X0是真C-拟凸,则称f是真C-拟凹. 定理1.2设X是紧的实Banach空间,E是可分实序Banach空间,若f∶X→E是上方下半连续,则minf(X)≠Ø. 证明:f(X)取中的所有全序子集 f(xα)∶α∈I ,I是指标集. 现在只需要证明 f(xα)∶α∈I 有下界. 因为E是可分,所以存在{f(xα)∶α∈I}的稠密子集{f(xn)∶n≥1},不妨假设f(x1)≥f(x2)≥…,又因为xn∈X和X是紧的,故{xn}有收敛子列,不妨设其为{xn}且xn→x0. 因f是上方下半连续,故有f(x0)≤f(xn),∀n≥1. 接下来要证f(x0)≤f(xα),∀α∈I. 对任意f(xα),由于E的可分性,存在子集{f(xn)} f(xn)→f(xα). 因f(x0)≤f(xni)和C是闭集,令i→+∞,故f(x0)≤f(xα),∀α∈I. 即{f(xα)∶α∈I}有下界. 由Zorn引理,可得minf(X)≠Ø. 注1.6 (a) 定理1.2结论得出广义半连续存在Pareto优化问题的解,进一步还可以得出minwf(X)≠Ø. (b) 若命题1.2中的f是C-下方上半连续,则maxf(X)≠Ø. (c) 若E=R,则得出广义Weierstrass 定理.这与文献[7]命题1.7结论相一致. (d) 若定理1.2的条件不变,f是真C-拟凸,则minf(X)是单值的. 事实上,若有x1,x2∈X使得f(x1),f(x2)∈minf(X),因f是真C-拟凸,令x(t)=tx1+(1-t)x2,t∈[0,1],则有 [0,1]={t∶f(x(t))≤f(x1)}∪{t∶f(x(t))≤f(x2)}, 现在先证{t∶f(x(t))≤f(x1)}是闭集. 任取{tn}⊂{t∶f(x(t))≤f(x1)}使得tn→t0. 故有f(x(tn))≤f(x1),从而f(x(tn))=f(x1). 因f是上方下半连续,故有 fx(t0)≤fx(tn). 即是f(x(t0))≤f(x1),故t0∈{t∶f(x(t))≤f(x1)}. 同理可得{t∶f(x(t))≤f(x2)}是闭集. 引理1.1[9]设X是实Banach空间,假设f,g∶X→E是两个向量值映射,f是连续的和g是序下半连续. 则f+g是序下半连续. 注1.7 (a)若引理1.1条件不变,由注1.2(c)可以知道f+g是C-上方下半连续. (b) 在文献[9]中,若f,g是C-下半连续,则f+g也是C-下半连续. 这一节,我们给出广义的半连续向量值函数的鞍点定理. 定理2.1设X和Y是紧的实Banach空间,E是可分实序Banach空间,假设f∶X×Y→E是一个向量值映射,若f(x,y)=u(x)+v(y),其中u是上方下半连续,v是下方上半连续. 则f至少有一个弱C-鞍点. 证明:由假设条件和定理1.2,可得 minwu(X)≠Ø,maxwv(Y)≠Ø. 所以,存在x0∈X,y0∈Y使得 u(x0)∈minwu(X)和v(x0)∈maxwv(Y), 因此,有 f(x0,y0)=u(x0)+v(y0)∈u(x0)+maxwv(Y)∩minwu(x)+v(y0)=maxwu(x0)+v(Y)∩minwu(X)+v(y0)=maxwf(x0,Y)∩minwf(X,y0). 这就证明了(x0,y0)是的一个弱C-鞍点. 注2.1 若定理2.1条件中E=R,则f(x0,y0)=minwf(x0,Y)=maxwf(X,y0). 定理2.2设X和Y是紧的实Banach空间,E是可分实序Banach空间,假设f∶X×Y→E是一个向量值映射,若f(x,y)=u(x)+β(x)v(y),其中u是连续,v是下方上半连续,β∶X→(0,+∞)是连续,则f至少有一个弱C-鞍点. 证明:由假设条件,可以找到一个y0∈Y使得v(y0)∈maxwv(Y). 由于u,β的连续性,从而x├→u(x)+β(x)v(y0)是连续. 因和是紧的实Banach空间,则存在使得 故f(x0,y0)∈minwf(X,y0). 另一方面,因β(x)>0,∀x∈X,我们有 β(x0)maxwv(Y)∈maxwβ(x0)v(Y),故f(x0,y0)∈maxwf(x0,Y) 所以(x0,y0)是的一个弱C-鞍点. 注2.2 显然定理2.2的结论是[9]中定理3.1的推广. 定理2.3设X和Y是紧的实Banach空间,E是可分实序Banach空间,假设f∶X×Y→E是一个向量值映射,若f(x,y)=u(x)+β(x)v(y),其中u是连续,v是序上半连续,β∶X→(0,+∞)是下半连续且C∩maxwv(Y)≠Ø,则f至少有一个弱C-鞍点. 证明:由假设v是序上半连续,从而v是C-下方上半连续,所以maxwv(Y)≠Ø. 由假设取一个y0∈Y使得v(y0)∈C∩maxwv(Y). 因u的连续性和β的下半连续,由引理1.1可以得出x├→u(x)+β(x)v(y0)是上方下半连续. 因X,Y是紧的实Banach空间和E是可分的,则存在x0∈X使得 从而f(x0,y0)∈minwf(X,y0). 接下来,按照定理2.2证明过程,可以得出f(x0,y0)∈maxwf(x0,Y). 证明完毕 注2.3 若定理2.3中的是C-下半连续,v是C-下方上半连续,其它条件不变,则结论依然成立. 下面证明一类广义向量值映射存在向量值平衡问题的解 定理2.4设X是紧的实Banach空间,E是可分实序Banach空间,假设f∶X×Y→E是一个向量值映射,其中f(x,y)=u(x)-u(y)∈X,若u是上方下半连续,则存在y0∈X使得 f(x,y0)∉-intC. 证明:由定理1.2可以知道,存在y0∈X使得 u(y0)∈minwu(X), 那么对任意x∈X,都有f(x,y0)=u(x)-u(y0)∉-intC,∀x∈X. 本文主要利用广义的半连续函数得出 Pareto问题优化解和获得鞍点定理,同时也推广了[7][9]的一些结果. [1] Corley H W. An existence result for maximizations with respect to cones[J]. J Optim Theory Appl, 1980, 31: 277-281. [2] Ferro F. A minimax theorem for vector-valued function[J]. J Optim Theory Appl, 1989, 60: 19-31. [3] Tanaka T. Generalized quasiconvecities, cone saddle points, and minimax theorem for vector-valued functions[J]. J Optim Theory Appl, 1994, 81(2): 355-377. [4] Finet C, Quarta L, Troestler C. Vector-valued variational principles[J]. Nonlinear Anal, 2003, 52:197-218. [5] Bednarczuk E M,Zagrodny D. Vector variational principle[J]. Arch Math, 2009, 93: 577-586. [6] Banachi M, Kassay G, Pini R. Ekeland’s principle for vector equilibrium problems[J]. Nonlinear Anal, 2007, 66: 1454-1464. [7] CHEN Y Q, CHO Y J, YANG L. Note on the results with lower semi-continuity[J]. Bull. Korean Math. Soc, 2002, 39(4): 535-541. [8] CHEN Y Q, CHO Y J, KIM J K. Minimization of vector-valued convex functions[J]. J Nonlinear Convex Anal, 2015, 16(10): 2053-2058. [9] Tanaka T. Generalized semicontinuity and existence theorems for cone saddle points[J]. Appl Math Optim,1997, 36: 313-322. [10] Gajek L, Zagrodny D. Weierstrass theorem for monotonically semicontinuous functions[J]. Optimization, 1994, 29: 199-203.
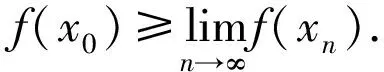

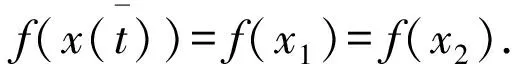
2 主要结果


3 结束语

