线性代数教学改革及创新应用能力的培养

徐洪香，刘秀娟，石月岩，宓 颖



线性代数教学改革及创新应用能力的培养

徐洪香，刘秀娟，石月岩，宓 颖

(辽宁工业大学 理学院，辽宁 锦州 121001)

主要从教学思维模式、教学内容、教学手段、考试形式和成绩评定等方面进行深入讨论，提出了鼎新传统教学模式、内容、手段等方面的方法，强调以面向应用为目标，以探求知识和应用知识为主的思维模式，探寻启发式、类比式、案例式的教学模式，充分应用计算机辅助技术等教学手段，通过考试形式的多样性和成绩评定的灵活性，全面反映学生的综合水平。是以，通过线性代数的教学改革，培养学生的学习主动性和参与性，提高学生分析问题和解决问题的能力。

线性代数；教学改革；创新应用能力

线性代数属于工科数学教学的三大骨干课程之一，不仅是高等职业院校开设的首要基础理论课，还是硕士研究生（工程、经济学等）的入学必考科目。这门课程具有逻辑性、抽象性、理论性强、课时少、内容多等特点，尤其是和以前的数学知识联系较少，学生学起来尤为困难。而由于一些学生的基础不够扎实，教学中内容的安排受数学专业的教学内容的影响较大，偏重于基本理论和基本概念的讲解，没有根据这些学生的水平和需要组织教学，导致部分学生对这门课程的学习积极性不高，学习效果较差，对应用性训练不足，轻视了对学生们创新应用能力的培养[2]。作为长期从事线性代数课程教学的教师，在教学过程中，我们一直在思考与探索，如何激励学生面对各种抽象的定义、定理，能给学生一种启迪、一种思维方法，面对各种实际问题不再束手无策。故而应当对传统的线性代数课程的教学思维模式、内容及方法进行改革，在教学中融入数学建模的思想、方法及内容，让学生在学习中体会生活中的应用，从而对这门课产生兴趣和学习的主动性，着重培养学生创新应用能力。

一、鼎新传统的教学思维形式

构建以探求知识、应用知识为主的教学思维模式。线性代数课程应该符合辽宁工业大学（以下简称我校）人才培养目标的要求，应定位在学生已驾驭一定的基本概念及理论的前提下，具有解决实际问题的创新和应用能力[4]。

传统的教学思维过程是：给出定义—证明定理和性质—运用方法和技巧运算—应用。教师为主体，以传授知识为主，按定义、引理、定理、推论的逻辑顺序进行，注重分析、推理、举例计算帮助理解概念和定理。因为课时少、内容多等缘故，往往没有应用学习的知识解决实际问题的过程，造成学生思维模式固定,无法拓宽其思路,忽视运用所学解决实际问题的能力训练，不清楚学习线性代数的用途，不能学以致用，阻碍了学生创新精神和创造性思维能力的形成。是以，要鼎新一直以来的教学形式，构建一个以探求知识、应用知识为主的教学思维模式：提出问题—观察和分析问题—验证—归纳结论、定理和性质—证明—解决问题。它以学生为主体，以传授数学思想、方法和用数学解决问题为主。先提出问题引起学生的兴趣，引导学生透过现象的观察分析，抓问题的本质，归纳结论，证明结论，进而解决提出的问题。这类教学思维形式非常容易引起学生学习的兴致，学习才更有动力，同时学生的创新思维能力和应用所学知识解决实际问题的能力进一步得到提高。

二、鼎新传统的教学内容

探寻启发式、类比式、案例式的讲授形式。

（一）教学要合理借助几何直观背景，降低学生抽象思维的难度

学习一条基本概念、一条定理或证明，如果借助几何图形、几何语言解释其直观含义或证明的直观思路，有助于学生从抽象到有形的过程，降低抽象思维的难度。

如：①二阶与三阶行列式的几何意义：二阶行列式等价于两个二维向量构成的平行四边形的面积；三阶行列式等价于三个三维向量构成的平行六面体的体积；

②向量组相关性的几何意义[3]：

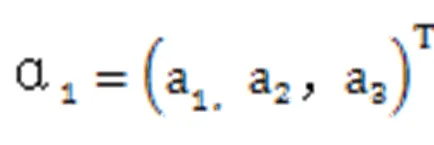
线性无关，且向量组

线性相关等价于三直线

相交于一点；

教材中很多知识都有其直观的几何意义，借助合理的几何直观背景，使学生易于理解掌握所学知识。

（二）注重引入实际应用或应用背景，使学生感受数学的趣味性和实用性

现今社会生活、生产实践中存在大量的材料，只须我们充分发掘，精心设计，就可以给出很多具备生活味浓厚的应用实例或应用背景，以使学生体味数学与生活的联系，老师介绍关键的定义、定理、例题时引入应用实例，激发学生的兴趣，使学生在一个迷人的叙述和解决问题中学习知识，了解数学的来源背景，领会数学的应用价值。如：

①学生课表、列车时刻表、产品的售价和重量对应矩阵表示问题；

②信息编码中的编制与破译问题对应逆矩阵问题；

③多次转机飞机航线问题对应矩阵的乘幂问题等等[1]。

（三）通过案例式教学模式，将数学建模的思想融入到课堂教学中

“教数学”是为了让学生理解“数学的思想”。因此，教学过程中灵活采用案例式教学模式，这是融入数学建模思想的一种非常有效的途径。老师有意识地结合教学内容和学生的实际水平制造实际问题的情景，依照数学建模的步骤，老师提出问题，让学生自己分析、假设，自己寻找数学概念、结论、规律，进而利用计算机等辅助手段解决实际问题，这种通过师生间互动、学生间互动的教学方式，能使学生感受到学习氛围是平等的、宽松的、新奇的、有趣味性的，同时实实在在感受线性代数课程“源于实践、用于实践”的本质。

教学案例的选择十分重要，选择的教学案例不但要根据课堂教学内容和教学目的要求，还要充分考虑案例是否实用、是否有趣味性、能否达到良好教学效果、不同专业学生是否有针对性等特点。如：

①对经济管理类专业的学生引入金融公司支付基金流动问题、投入产出问题等案例；

②对电子信息工程类专业的学生引入平板稳态温度分布问题、电路设计问题等案例；

③对交通工程类专业的学生引入交通流分析问题等案例，等等[1]。

通过选择学生熟悉的、感兴趣的案例，使学生能更快的理解和掌握相关的数学知识，教材中很多知识点非常适合案例式教学。如：线性方程组是否有解问题的研究；向量组是否线性相关问题的研究；矩阵乘法等知识点都适合用案例式教学模式。

三、鼎新传统的教学手段，灵活采用多媒体教学和数学实验

目前，我校线性代数课程安排40学时，而内容较多，特别是矩阵的初等变换运算占用了大量的时间。教学手段还是老师玩粉笔，新的计算机技术基本上不进课堂，课堂上的信息量较少，呈现出沉闷的方式，老师基本上是为完成教学内容而教学，很少与学生互动，对部分内容较少进行详细的分析和讲解，抽象的内容也不能直观地反映。尤其是案例式教学内容，涉及分析、假设、归纳、论证、解决这样一个完整的建模过程，内容较多，如果老师采用传统教学手段，很难体现符合学生思维的猜测、尝试、验证、分析和综合的过程。是以，灵活的多媒体辅助教学手段非常必要，通过多媒体课件的形式，把教学中的重点和难点进行归纳总结，使学生对所学知识通过相互间的关联，使整个知识体现的建立过程有更清晰的认识。复习课和习题课也通过生动的多媒体动画展示，抽象的知识具体化，即增强教学趣味性，又增加课堂信息量。

有很多案例式教学内容根据实际问题需要，做推广和扩展性研究，因而建立的数学模型就更为复杂，求解相当麻烦。那么，教学中适时利用数学工具软件Matlab实施数学实验，是十分必要的。如：板式热导体稳态温度分布的问题是将板分成多个正方形，只要测量矩形板四周的温度，就可以确定板上各点的温度。通过建立阶数与节点数相同的四元线性方程组，结合平板的边界条件就可以求解方程组[1]。平板分割越细，求出的解越精确，而建立的方程组的阶数就越高，方程组越难求解，通过数学实验，利用Matlab强大的统计、分析和演示功能，不但可以快速求解高阶线性方程组，而且可直观地绘制温度分布图形，教学效果非常好。

四、考试形式多样性、成绩评定灵活性，全面反映学生的综合水平

目前，我校线性代数课程采用期末闭卷考试和平时考核两种方式。其中，85%为期末成绩，15%为平时成绩。闭卷考试的考核重点是对学生的基本概念、定理把握程度的考察，要求学生完成考卷中的一些计算或证明。平时成绩主要考核学生的作业和上课出席情况，基本上没有与学生阶段性对知识理解掌握程度联系起来，这种考核方式只会导致学生死记硬背，被动学习，没有学习兴趣，所以目前的考核方式存在一定的弊端。是以，有必要改革目前的考核方式，即：闭卷和开卷灵活应用：基本概念、定理和公式的理解等基本理论部分掌握程度仍然采用闭卷考核方式；开卷部分主要考察学生的数学建模能力，通过应用性、综合性较强且能通过编程或利用Matlab求解的实际案例，要求学生依据数学建模的步骤完成小论文或活动报告，可独立完成或分组完成，着重考核学生面对实际问题分析假设、选择数学方法、解决问题的应用创新能力。

笔试与口试灵活应用：课堂增强提问环节，重点知识随时提问，加强口试环节的训练。同时，每一章节内容安排小测验，加强阶段性知识环节的掌握。

成绩评定灵活化：期末成绩约占70%，闭卷考核基础理论部分；平时成绩约占30%。平时成绩可根据课堂作业、课堂提问、小测验、小论文或活动报告等考核方式。各部分所占比例可按课堂作业占30%，课堂提问占10%，小测验占30%，小论文或活动报告占30%的份额分配。只有通过这种多样性的考核方式以及灵活性的成绩评定方法，才能全面考核学生的综合实际水平。

五、结束语

通过对线性代数教学改革，既可以让学生们巩固基础知识，又可以让他们尝试理论联系实际，应用数学建模的思想和方法将所学知识灵活运用到实际中去，提高学生分析问题和解决问题的能力。

[1] 黄玉祷，彭涛. 线性代数中矩阵的应用典型案例[J]. 兰 州大学学报，2009,45(3)：123-125.

[2] 郭竹梅. 应用型本科院校“线性代数”课程教学改革探讨[J]. 吉林工程技术师范学院学，2011,27(4)：29-31.

[3] 同济大学数学系编.线性代数[M].6版. 北京：高等教育出版社，2014: 2-115.

[4] 夏建国. 技术应用性本科院校办学定位的特征分析[J]. 中国高教研究，2008(6): 58-60.

(责任编校：付春玲)

2016-05-26

徐洪香(1963-)，女(满族)，辽宁绥中人，副教授。

http://kns.cnki.net/kcms/detail/21.1566.C.20171106.1459.002.html

10.15916/j.issn1674-327x.2017.06.032

G642.41

B

1674-327X (2017)06-0108-03