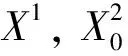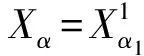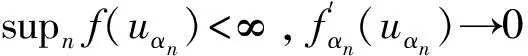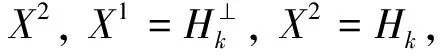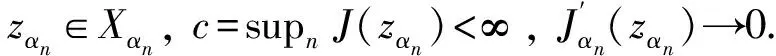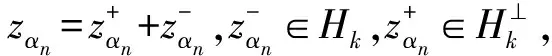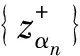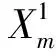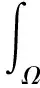含次临界Sobolev指数半线性合作椭圆方程组非平凡解的存在性
樊自安, 寇继生
(湖北工程学院 数学与统计学院, 湖北 孝感 432000)
0 引 言
近年来, 关于合作椭圆方程组解的存在性被广泛的研究. Silva用鞍点定理在文献[1]中研究了Hamiltonian系统的解的存在性. Furtado 在文献[2]中研究了方程组
解的存在性. 相关论文还可参考文献[3-9]. 文献[10-13,15-17]利用Nehari流形的方法得到了椭圆方程的多解性.
本文主要研究下列椭圆方程组
(1)

当λ=1,a(x)=b(x)=c(x)=1时, 问题(1)相当于文献[15]的情形, 本文应用Nehari流形和局部环绕定理证明了当2 设(u,v), (φ,ψ)∈E, 定义算子T∶H→H* 其中 则算子T是对称的有界线性算子. 由Sobolev紧嵌入定理可知T是紧算子. 考虑特征值问题(2) (2) 则λ是问题(2)的特征值当且仅当T(u,v) =λ-1(u,v). 问题(2)存在一系列特征值 0 <λ1<λ2≤…≤λk≤…,k=1,2,…, 成立. 详见文献[3,5]. 定义1 (u,v)∈E是问题(1)的一个弱解, 是指任意(φ1,φ2)∈E满足 下面为本文的主要结果. 定理1 假设0 <λ<λ1, 则问题(1)存在一个非平凡解. 定理2 假设λk<λ<λk+1, 则问题(1)存在一个非平凡解. 定义能量泛函 2b(x)uv+c(x)v2)dx- 其中 则J∈C1(E,R). 考虑Nehari流形Nλ={(u,v)∈E{(0,0)}|〈{J′(u,v),(u,v)〉=0}, 因此, (u,v)∈Nλ, 当且仅当 〈J′(u,v),(u,v)〉‖(u,v)‖2-A(u,v)- K(u,v)=0. 对于(u,v)∈Nλ, 有 于是,J(u,v)是有下界的. 定义 M(u,v)=〈J′(u,v),(u,v)〉. 对于(u,v)∈Nλ, 有 〈M′(u,v),(u,v)〉= 2(‖(u,v)‖2-A(u,v))-pK(u,v)= (2-p)K(u,v)=(2-p)‖(u,v)‖2- (2-p)A(u,v).(3) 把Nλ分成3个部分, 即 证明此证明类似于文献[13]所述, 故略去证明. 由于(u,v)∈Nλ时,J(u,v)是有下界的, 我们可以定义 引理2 当0 <λ<λ1, 存在C0=C0(λ,λ1,p,S0)>0, 使得ξ->C0. 由式(4), (5)得 (6) 于是由式(4),(6)得,ξ->C0. 则有下列引理. 证明对于(u,v)∈E, 且K(u,v)>0, 设 h′(t)=t(‖(u,v)‖2-A(u,v))-tp-1K(u,v). 令h′(t)=0, 得到t=t0,h(0)=0,t→+ ∞,h(t)→-∞. 当t∈[0,t0),h′(t)>0; 当t∈[t0,∞),h′(t)<0, 因此h(t)在t=t0时达到最大值. 〈M′(t0u,t0v),(t0u,t0v)〉= 由式(4)知 (7) 现在考虑λk<λ<λk+1的情形. 设X是一个实Banach空间,X=X1⊕X2, 设 定义3 设X是一个Banach空间,X=X1⊕X2, 泛函f∈C1(X,R)在0处关于(X1,X2)局部环绕, 假如存在r>0使得 f(u)≥0, ∀u∈X1,‖u‖ ≤r; f(u) ≤ 0, ∀u∈X2, ‖u‖ ≤r. 引理5 设X是一个Banach空间,X=X1⊕X2, 泛函f∈C1(X,R)满足下列条件: 1) 泛函f在0处关于(X1,X2)局部环绕; 2) 泛函f满足(PS)*条件; 3) 泛函f从有界集映为有界集; 4) 对于∀m∈N, 当u∈Xm1⊕X2, ‖u‖→∞时,f(u)→- ∞; 则泛函f至少有一个非平凡的临界点[16]. 设(u,v)∈E, 定义泛函 其中 2b(x)uv+c(x)v2)dx, 则J∈C1(E,R). 定理2的证明第一步,J∈C1(X,R), 泛函J在0处关于(X1,X2)局部环绕. 由于p>2, 存在足够小的r1>0, 使得当‖z‖ ≤r1时,J(z)≥0. 另外, 对于z∈X2=Hk, 当λk<λ<λk+1时, 即存在r2>0, 使得当‖z‖ ≤r2,J(z) ≤0. 取r=min{r1,r2},J在0处关于(X1,X2)局部环绕. 第二步, 泛函J从有界集映为有界集. 第三步, 泛函J满足(PS)*条件. 2J(zαn)-〈J′(zαn),zαn〉= (9) 由Hölder不等式及式(8),(9)得, 当n充分大时, ‖zαn-z‖2=〈J′(zαn-z),zαn-z〉+ 因此, {zαn}存在收敛的子列. M1‖z‖2≤ ‖z‖ ≤M2‖z‖2.(10) 于是 其中,M0=max{max|a(x)|, max|b(x)|, max|c(x)|}. 由于2 故对于任意M>0, 存在C(M)>0使得 |s|p≥M|s|2-C(M), ∀s∈R2, a.e.x∈ΩRn.(12) 由式(10)~(12)得, 当λk<λ<λk+1,M足够大时, 有 [1] Silva E. Subharmonic solutions for subquadratic Hamiltonian systems[J]. Journal of Differential Equations, 1995, 115(1): 120-145. [2] Furtado M F, Mala L A, Silva E A B. Solutions for a resonant elliptic system with coupling inRN[J]. Communications in Partial Differential Equations, 2002, 27(7-8): 1515-1536. [3] Furtado M F, Paiva F O V D. Multiplicity of solutions for resonant elliptic systems[J]. Journal of Mathematical Analysis Applications, 2006, 319(2): 435-449. [4] Ma T F, Ramos M, Sanchez L. Multiple solutions for a class of nonlinear boundary value problems near resonance: a variational approach[J]. Nonlinear Analysis, 1997, 30(6): 3301-3311. [5] Chang K C. Principal eigenvalue for weight matrix in elliptic systems[J]. Nonlinear Analysis, 2001, 46(46): 419-433. [6] Rabinowitz P. Minimax methods in critical point theory with applications to differential equations[M]. Washington: The American Mathematical Society, 1986. [7] Duan Shengzhong, Wu Duanxian. Existence of solutions for a class of semilinear elliptic systems[J]. Nonlinear Analysis, 2010, 73: 2842-2854. [8] Ou Z Q, Tang C L. Existence and multiplicity results for some elliptic systems at resonance[J]. Nonlinear Analysis, 2009, 71(7): 2660-2666. [9] Alves C O, Filho D C D M, Souto M A S. On systems of elliptic equations involving subcritical or critical Sobolev exponents[J]. Nonlinear Analysis, 2000, 42(5): 771-787. [10] Brown K J, Wu T F. A semilinear elliptic system involving nonlinear boundary condition and sign-changing weight function[J]. Journal of Mathematical Analysis Applications, 2008, 337(2): 1326-1336. [11] Adriouch K, Hamidi A E. The Nehari manifold for systems of nonlinear elliptic equations[J]. Nonlinear Analysis Theory Methods Applications, 2006, 64(10): 2149-2167. [12] Alves C O, Hamidi A E. Nehari manifold and existence of positive solutions to a class of quasilinear problems[J]. Nonlinear Analysis, 2005, 60(4): 611-624. [13] Wu T. On semilinear elliptic equations involving concave-convex nonlinearities and sign-changing weight function[J]. Journal of Mathematical Analysis Applications, 2006, 318(1): 253-270. [14] Li S J, Willem M. Applications of local linking to critical point theory[J]. Journal of Mathematical Analysis Applications, 1995, 189(1): 6-32. [15] 樊自安,包含次临界和临界Sobolev指数的椭圆方程组解的存在性[J]. 应用数学学报, 2015, 5(38): 835-844. Fan Zian. Existence of solutions for elliptic systems involving subcritical or critical Sobolev exponents[J]. Acta Mathematicae Applicatae Sinica(A), 2015,5(38): 835-844. (in Chinese) [16] Qi Z, Zhang Z. Existence of multiple solutions to a class of nonlinear Schrodinger system with external sources terms[J]. Journal of Mathematical Analysis Applications, 2014, 420(2): 972-986. [17] Nyamoradi N, Hsu T S. Existence of multiple positive solutions for semilinear elliptic systems involving critical hardy-sobolev exponents and sign-changing weight function[J]. Acta Mathematica Scientia(B), 2014, 17(2): 330-350.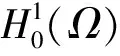

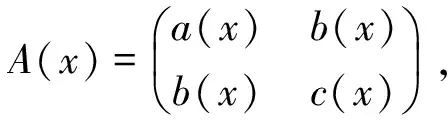
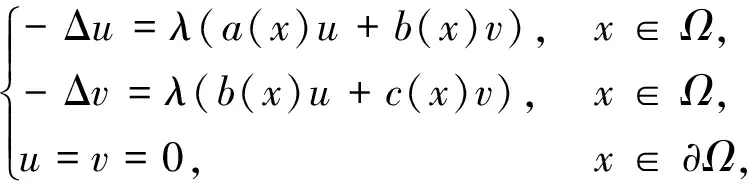
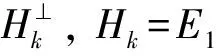
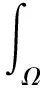
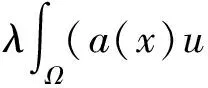
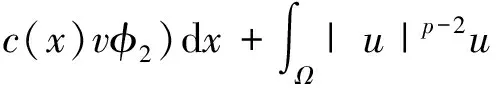
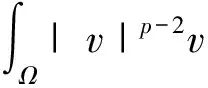
1 定理1的证明
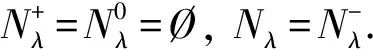
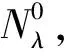

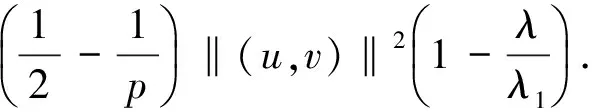

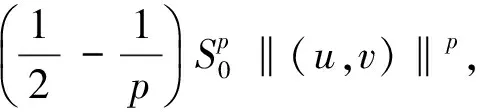
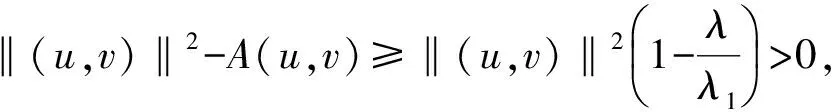


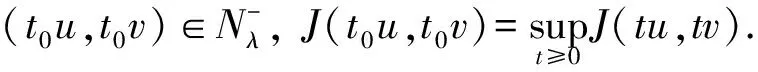

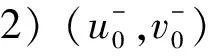
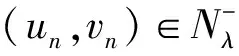
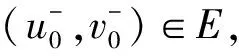



2 定理2的证明