海底输气管道泄漏扩散模拟及正交试验分析
,,,
(中国石油大学 机电工程学院,山东 青岛 266580)
由于海洋环境恶劣,海底管道受到腐蚀、波浪冲刷、第三方破坏和海床运动等因素的影响,极易发生穿孔、裂缝及断裂等失效[1-2],引起海底输气管道的泄漏,造成环境污染和经济损失。因此,对海底输气管道泄漏扩散规律进行研究,对泄漏事故的应急处理和环境风险分析都具有重要意义。
目前,管道泄漏的研究集中在陆地管线方面,海底天然气管道泄漏扩散的问题涉及较少。国内外学者针对泄漏模型和扩散规律进行了相关研究[3-7],探究了影响海底输气管道泄漏扩散规律的因素。这些研究对水下气体泄漏的数值模拟与分析着重在考察各影响因素对天然气扩散形态的影响,对某一结果指标而言,不能确定各影响因素的主次关系。对海底天然气管道泄漏扩散规律研究仍需要进行大量数值模拟和试验分析。由于影响泄漏气体扩散的因素较多,单因素逐个分析需要消耗大量计算时间,需要采取更加快速高效的方式进行相关研究。本文采用正交试验法对影响海底泄漏天然气扩散规律的气体泄漏速度、洋流速度和泄漏孔径尺寸3个因素进行试验设计,使用综合比较法与方差分析法确定了影响气体扩散范围和到达海面时间影响因素的显著情况。
1 控制方程
流体泄漏扩散过程中普遍遵守质量守恒方程、动量守恒方程和能量守恒方程[8-9]。
质量守恒方程:
(1)
式中:ux、uy、uz分别为x、y、z方向的速度分量,m/s;t为时间,s;ρ为密度,kg/m3。
动量守恒方程:

(2)
式中:p为流体微元体上的压力,Pa;ui、uj为相应坐标系上的速度分量,m/s;xi、yj为相应方向坐标;τij为因分子黏性作用而产生的作用在微元体表面上的黏性应力τ的分量,Pa;Fi为相应方向上的单位质量力,m/s2。
能量守恒方程:

(3)

2 正交试验设计
海底输气管道泄漏事故可分为泄漏、穿孔和破裂3类,前两者的发生概率分别为54%和29%,是海底输气管道的主要破坏形式[10],因此,数值模型选取0.02 、0.05和0.10 m 3种泄漏孔径尺寸,以研究泄漏孔径对泄漏气体扩散规律的影响。泄漏孔形状对泄漏气体的扩散规律也有一定影响,此处假定所有泄漏孔均为圆形。
天然气泄漏速度和管道上方水体压力、管道内压和天然气流经泄漏孔时的压降等因素有关[11-12],为了考察天然气泄漏速度的影响,参考海底气田生产常见压力工况[5,13],选取压力为4.5 MPa,温度为20 ℃,计算天然气泄漏速度约为250 m/s,设置参考组的泄漏速度为180 m/s和320 m/s,且假设气体泄漏速度为定值。
为考察洋流运动对泄漏气体扩散规律的影响,设置洋流速度为0.1 0、0.25和0.50 m/s进行模拟试验[14]。
最终选取的因素及其水平如表1所示:

表1 海底管道天然气泄漏扩散因素水平
针对三因素三水平的问题,使用控制变量进行单因素逐个分析,需要进行32次试验,使用正交试验法,只需进行9次模拟试验,可以节省2/3的模拟时间。
选用L9(34)正交表安排试验,选取第1、2和3列进行试验设计,第4列作为对试验误差的粗略估计[15]。试验方案设计如表2所示。

表2 正交试验方案设计参数
3 模型设置
在沿洋流方向,泄漏气体具有最大扩散半径,因此选取沿洋流方向的切面为研究平面,进行二维模拟[16]。
计算区域设置为:水深与水面宽度皆为100 m,泄漏孔在距离左侧边缘40 m处。泄漏孔径分别为0.02、0.05和0.10 m。使用ICEM CFD软件进行网格划分,采用了三角形网格类型,对泄漏口区域及气泡扩散影响区域网格进行了加密处理。
边界条件设置为:泄漏口处设置为气体速度入口(velocity-inlet),泄漏速度为180 、250和370 m/s;计算区域底部设置为壁面(wall);为考虑洋流速度的影响,设置左侧为洋流速度入口(velocity-inlet),洋流速度分别选取为0.10、0.25和0.50 m/s。右侧为洋流自由出流边界(outflow),顶部边界作为水面,边界条件设置为压力出口(pressure-outlet),顶部压力边界条件值为0 Pa。
计算区域与边界条件设置如图1所示。

图1 计算区域与边界条件
CFD软件计算方法设置为:基于压力的求解器,采用瞬态算法求解泄漏气体扩散过程,启用VOF模型并开启隐式体积力,湍流模型采用标准κ-ε模型。压力-速度耦合采用PISO算法,对流项使用二阶迎风格式,扩散项使用中心差分格式,压力插值方法使用体积力分数计算。初始相设置为计算区域充满海水。
4 数值模拟结果及分析
4.1 综合分析
泄漏初始阶段,气体受到海水压力作用,在泄漏孔上方形成气团,图2为各试验方案在气体泄漏2 s后泄漏孔上方形成的气团图,通过比较图2(a、b、c)、图2(d、e、f)和图2(g、h、i)可以看出,气团大小与泄漏孔径尺寸关系密切,泄漏孔径尺寸越大,形成的气团半径越大。通过比较图2(a、d、g)、图2(b、e、h)和图2(c、f、i)可以看出,气团大小亦受泄漏速度影响,泄漏速度越大,气团越大,但泄漏速度的影响显著情况低于泄漏孔径尺寸。通过比较图2(a、e、i)、图2(b、f、g)和图2(c、d、h)可以看出,初始气团形态及大小与洋流速度关系不明显。


图2 气体泄漏2 s后气体分布
气团形成后,在浮力、惯性力和洋流作用力等力的共同作用下,开始分散和破碎成气泡,并向上迁移,气泡羽流范围亦随之不断扩大,大气团不断分散破碎成小气泡,与海水混合程度增加。单位时间内的气体泄漏量受泄漏孔径、泄漏速度影响,导致水体中气团形态不同。图3为泄漏15 s后各模拟试验的气体泄漏状态。从图3(a、b、c)、图3(d、e、f)和图3(g、h、i)可以看出,气体与海水混合程度受泄漏孔径尺寸影响明显,泄漏孔径越大,气体与海水混合程度减小,气泡半径越大;从图3(a、d、g)、图3(b、e、h)和图3(c、f、i)可以看出气体与海水混合程度亦受泄漏速度影响,泄漏速度增大,气体与海水混合程度减小,气泡半径增大,但泄漏速度的影响显著情况低于泄漏孔径尺寸。此现象是由于气体泄漏量增大,导致涡流作用增强,泄漏气体受水流作用影响相对减小,因此气团向上扩散时气泡半径更大。
受泄漏条件的影响,泄漏气体在气泡尺寸、气团形态、到达海面所需时间、扩散范围等方面均有所不同。图4展示了泄漏气体到达海面时的气体形态及泄漏气体到达海面所需的时间。从图4(a、b、c)、图4(d、e、f)和图4(g、h、i)可以看出泄漏孔径尺寸越大,泄漏气体与海水混合程度越小。气泡尺寸越大,泄漏气体到达海面时间越短;比较图4(a、d、g)、图4(b、e、h)和图4(c、f、i)可以看出,泄漏速度越大,泄漏气体与海水混合程度越小,气泡尺寸越大,泄漏气体到达海面时间越短。比较图4(a、e、i)、图4(b、f、g)和图4(c、d、h)可以看出,洋流速度对泄漏气体最大扩散范围有影响,对气泡形态、气体与海水混合程度等其他指标影响不明显。


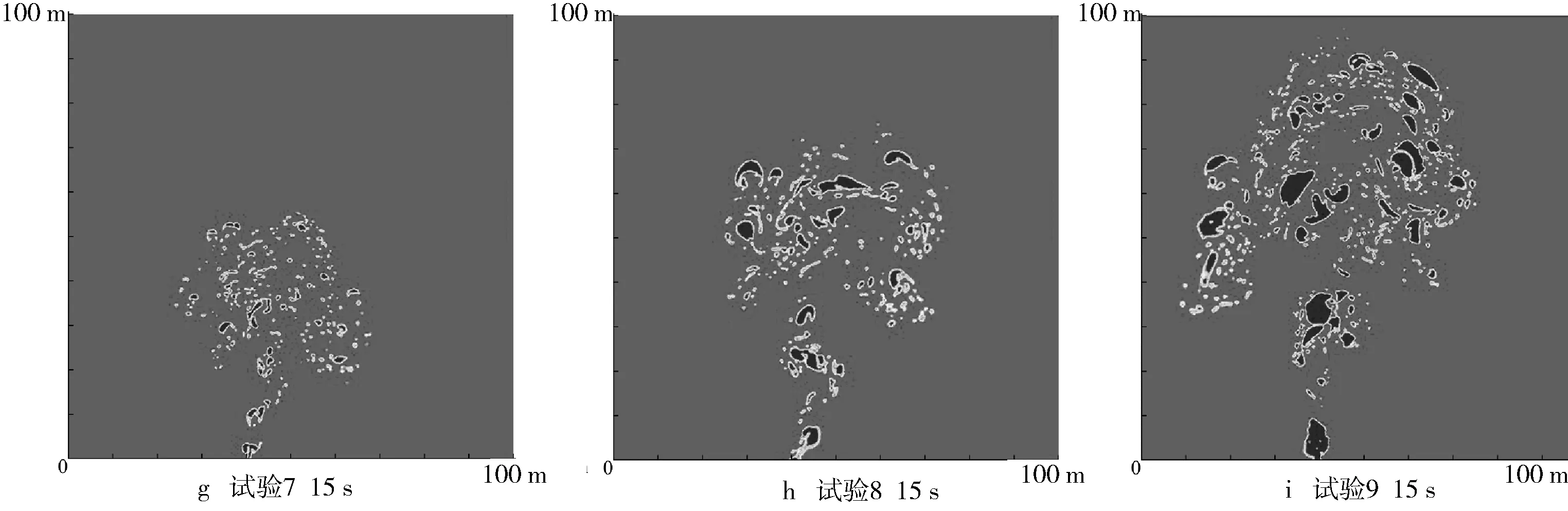
图3 气体泄漏15 s后气体分布



图4 泄漏气体到达海面时气体分布
4.2 方差分析
通过综合对比分析模拟结果,可以看出各影响因素对泄漏结果的影响,但是不能确定各影响因素对试验指标的主次关系及显著情况。为了确定各影响因素的主次关系与显著性,需要针对具体指标进行进一步比较分析。
根据数值模拟结果,分别以泄漏气体到达海面时间、最大扩散范围为试验指标,以两者的数值加和作为综合试验指标,采用综合比较法和方差分析法进行分析,确定影响试验指标的因素的主次关系及各因素显著情况。试验方案设计及结果分析如表3所示。

表3 试验方案设计及结果分析

表3(续)
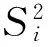
1) 以泄漏气体到达海面时间为指标,从表3可以看出,极差R最大的因素为泄漏孔径尺寸,其次为泄漏速度,各因素的主次关系为:
泄漏孔径尺寸>泄漏速度>洋流速度>其他因素为评价结果中各因素的显著情况,进行方差分析。方差分析表如表4所示。

表4 方差分析数据一(泄漏气体到达海面时间为指标)
对于给定的水平α=0.1,查F(2,2)分布表可得λ=9,由表4可知,以泄漏气体到达海面时间为指标,泄漏速度与泄漏孔径尺寸为影响结果的显著因素,洋流速度为非显著因素。
2) 以泄漏气体最大扩散范围为衡量指标,从表3可以看到,极差R最大的因素为洋流速度,其次为泄漏孔径尺寸,各因素的主次关系为:
洋流速度>泄漏孔径尺寸>其他因素>泄漏速度
方差分析表如表5所示。

表5 方差分析数据二(泄漏气体最大扩散范围为衡量指标)
对于给定的水平α=0.1,查F(2,2)分布表可得λ=9,由表5可知,以泄漏气体最大扩散范围为衡量指标,在该模拟条件下各考察因素的影响因素皆不显著,说明综合分析法存在一定的误差,泄漏气体最大扩散范围受多指标综合影响。
3) 以泄漏气体到达海面时间和最大扩散范围的数值加和为综合试验指标,从表3可以看出,极差R最大的因素为泄漏孔径尺寸,其次为洋流速度,各因素的主次关系为:
泄漏孔径尺寸>洋流速度>泄漏速度>其他因素方差分析表如表6所示。

表6 方差分析数据三(泄漏气体到达海面时间和最大扩散范围的数值加和为综合试验指标)
对于给定的水平α=0.1,查F(2,2)分布表可得λ=9,由表6可知,综合考察泄漏扩散的试验指标,泄漏孔径尺寸与洋流速度为影响结果的显著因素,泄漏速度对所考察的试验指标影响不显著。
5 结论
1) 采用正交试验法设计了海底输气管道的泄漏模拟方案,利用CFD软件进行了模拟试验。对试验结果进行综合比较与方差分析。
2) 在泄漏初始阶段,泄漏孔尺寸与泄漏速度影响气团形态,泄漏孔径与泄漏速度越大,气团半径越大;泄漏孔径与泄漏速度越大,气体与海水混合程度越小,气泡半径越大。
3) 以泄漏气体到达海面时间为指标,泄漏速度与泄漏孔尺寸对结果有显著影响;以泄漏气体扩散范围为指标,洋流速度与泄漏孔径尺寸均有影响,但二者都为非显著因素;综合考察泄漏扩散的试验指标,泄漏孔径尺寸与洋流速度为影响结果的显著因素,泄漏速度为非显著因素。
4) 使用正交试验法与数值模拟相结合的模拟研究方式,减少了模拟试验次数,节省了模拟计算时间,提高了计算效率,对探究海底泄漏气体扩散规律提供了参考,可为海底管线泄漏的风险预测、风险评估提供理论依据。
[1] 金伟良,张恩勇,邵剑文,等.海底管道失效原因分析及其对策[J].科技通报,2004,20(6):529-533.
[2] Mao D,Chu G,Yang L,et al.Deepwater Pipeline Damage and Research on Countermeasure[J].Aquatic Procedia,2015,3:180-190.
[3] 景海泳,余建星,杜尊峰,等.海底管道水下气体扩散FLUENT仿真分析[J].海洋技术学报,2012,31(3):82-85.
[4] 文闯,延斌,王宪全,等.海底管线天然气泄漏过程数值模拟[J].常州大学学报(自然科学版),2015,27(2):72-77.
[5] 李新宏,朱红卫,陈国明,等.海底管道泄漏天然气扩散规律数值模拟[J].油气储运,2016,35(2):215-220.
[6] Yapa P D,Dasanayaka L K,Bandara U C,et al.Modeling the impact of an accidental release of methane gas in deepwater[C].Oceans.IEEE Xplore,2008:1-10.
[7] Yapa P D,Zheng L,Chen F.A model for deepwater oil/gas blowouts[J].Marine Pollution Bulletin,2001,43(7-12):234-241.
[8] 朱红钧.FLUENT 15.0流场分析实战指南[M].北京:人民邮电出版社,2015:2-3.
[9] 吴望一.流体力学.上册[M].北京:北京大学出版社,1982:145.
[10] 窦梓元.水体中天然气管道泄漏扩散规律及后果分析[D].成都:西南石油大学,2015:26-27.
[11] Dong Y,Gao H,Zhou J,et al.Mathematical modeling of gas release through holes in pipelines[J].Chemical Engineering Journal,2003,92(1):237-241.
[12] 霍春勇,董玉华,余大涛,等.长输管线气体泄漏率的计算方法研究[J].石油学报,2004,25(1):101-105.
[13] 张淑艳,李伟,郭智阳.海底输气管道平均压力的计算与研究[J].中国海洋平台,2013,28(3):33-36.
[14] 刘延鑫,王旱祥,王苗.海底管道局部冲刷数值模拟分析[J].中国石油大学学报(自然科学版),2012(6):118-122.
[15] 常兆光,王清河,杜彩凤.应用统计方法[M].北京:石油工业出版社,2009:167-176.
[16] Zhu H,Lin P,Pan Q.A CFD (computational fluid dynamic) simulation for oil leakage from damaged submarine pipeline[J].Energy,2014,64(1):887-899.

