带GARCH误差项非线性ESTAR模型的单位根检验

胡俊娟，王 伟

(浙江科技学院 理学院，杭州 310023)

近年来，非线性模型受到了国内外研究者的广泛关注[1-3]。然而，对线性模型的单位根检验已经不适用于非线性STAR模型。因此，许多研究者对指数STAR(ESTAR)模型进行了探讨。Kapetanios等[4]提出了Dickey-Fuller型KSS检验统计量；Kruse[5]在位置参数取值任意的情况下，用修正的Wald统计量对ESTAR模型进行了研究；Hanck[6]修正了Kapetanios等提出的KSS检验统计量在带趋势项情况下的极限分布。张凌翔等[7]讨论了局部随机游走STAR模型、局部随机趋势STAR模型的线性检验问题，构造了 Wald类检验统计量，提出了在局部平稳性未知的条件下进行STAR模型的线性检验方法。在实际研究中，经济变量的波动在不同时期通常具有时变性和波动集群性，因此非线性STAR-GARCH 模型在现实中有着很重要的应用[8]。近年来, 对带GARCH误差项模型的单位根检验引起了研究者的广泛关注，参见Ling和Li[9]、 Wang[10]、 Yuan和Zhang[11]等。这些研究主要针对AR-GARCH模型的单位根检验进行了研究，然而针对STAR-GARCH模型的单位根检验，却鲜有文献提及。由于非线性的ESTAR-GARCH过程和带GARCH的单位根过程数据表现非常相近，为了有效地建立合适的模型，在对数据建模前应对其进行单位根检验。因此，对ESTAR-GARCH模型的单位根检验进行研究是必要的。我们拟采用KSS型检验统计量，将其表示成自标准化的部分和形式，从而推导出在有均值和无均值2种情况下该统计量的渐进分布。通过蒙特卡罗模拟验证了该统计量的检验效果，并将该检验统计量与常规的DF检验统计量进行比较。

1 关于平稳ESTAR过程的单位根检验

对于时间序列，Kapetanios等[4]361对一阶ESTAR模型(ESTAR(1))进行检验：

Δyt=γyt -1G(yt -1;θ)+εt,t=1,…,T。

(1)

1.1 Kapetanios等关于平稳ESTAR模型的单位根检验

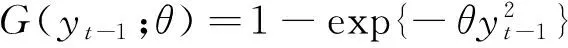
进一步，为了解决误差项相关问题，Kapetanios等[4]365通过增加Δyt的滞后项来消除。即考虑以下ESTAR(k)模型：

(2)

(3)

对模型(2)，Kapetanios等[4]363基于式(3)提出了Dickey-Fuller型t统计量进行单位根检验：

(4)

1.2 关于ESTAR-GARCH模型的单位根检验

考虑以下带GARCH误差项的ESTAR模型(ESTAR(k)-GARCH(p,q)模型)：

(5)

(6)

式(6)中：ω>0；αi≥0；βj≥0；i=1,…,p；j=1,…,q；et为独立同分布且均值为0，方差为1的序列。显然，当所有的αi和βj为零时，εt变成均值为零，方差为常数的独立同分布序列。

对于上述的ESTAR(k)-GARCH(p,q)模型(式(5)～(6))，通过对平滑转换函数的一阶泰勒展开，得到相应的辅助方程为：

(7)

相应地，在GARCH(p,q)误差项情况下，采用KSS型检验统计量来检验原假设H0:θ=0(即检验H0:δ=0)，记为τ：

(8)

(9)

(10)

(11)

接着讨论统计量τ和τu的渐进分布。为了考察ESTAR-GARCH模型，不妨把GARCH(p,q)模型的严平稳性作为必要条件事先给定, 首先给出用于推导渐进分布的假设1和假设2。

假设2多项式ρ(z):=1-ρ1z-…-ρkzk满足ρ(z)=0的根在单位圆外。

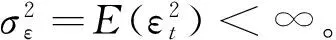
引理1在假设1成立的情况下，则

证明：根据文献[11]的引理5.1和引理5.2,可以得出，在假设1成立的条件下，

且对于任意的x>0,

根据Hall等[14]的定理4.1，可以得到

得证。

定理1在假设1和假设2成立的条件下，考虑非线性ESTAR(k)-GARCH(p,q)模型 (式(5)～(6))，统计量τ在原假设H0:θ=0下的渐进分布为:

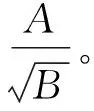
(12)

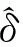
(13)

(14)

进一步，则有

Q1+Q2+Q3+Q4

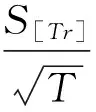
定理2在假设1和假设2成立的条件下，考虑非线性ESTAR(k)-GARCH(p,q)模型(式(9)～(11))(u≠0)，统计量τu在原假设H0:θ=0条件下的渐进分布为:

(15)

证明：考虑序列去掉漂移项。在原假设H0:θ=0的条件下, 根据最小二乘法，检验统计量为：

(16)

根据引理1和连续映射定理[18]，则有

得证。

2 Monte Carlo 模拟

从上述检验统计量的渐进分布可以看出，在单位根检验下, 该分布与模型中的参数无关。为此，我们采用Monte Carlo随机模拟方法，考察检验统计量τ和τu的检验效果。

首先考察以下几种不同的数据生成过程。数据生成过程设为：

yt=yt -1+εt,

其中：{et}～i.i.d.(0,1)；(ω,α1,β1)={(1,0,0),(0.1,0.2,0.7),(0.1,0.1,0.8),(0.1,0.05,0.9)}。这里考虑不同的GARCH模型系数(误差项εt是独立同分布和异方差情况)。为了考察不同情况统计量的渐进分布，蒙特卡罗模拟过程的数据样本容量设为1 000，重复50 000次。从定理1和定理2可以看出，检验统计量τ和τu的渐进分布与滞后项k无关，即对模型(5)和模型(10)而言，有无滞后项k都不会影响检验统计量的渐进分布。因此，在这里主要关注没有滞后项的情况。考虑到统计量的渐进分布与误差项GARCH模型中p,q无关，根据实际应用取p=q=1来进行讨论。图1给出了原始数据和去均值数据对应检验统计量τ和τu的经验累积分布。显然，无论在误差项为独立同分布序列还是GARCH情况下，检验统计量的渐进分布是一致的。相对而言，带漂移项的情况下，统计量的绝对临界值比无漂移项情况下稍大。

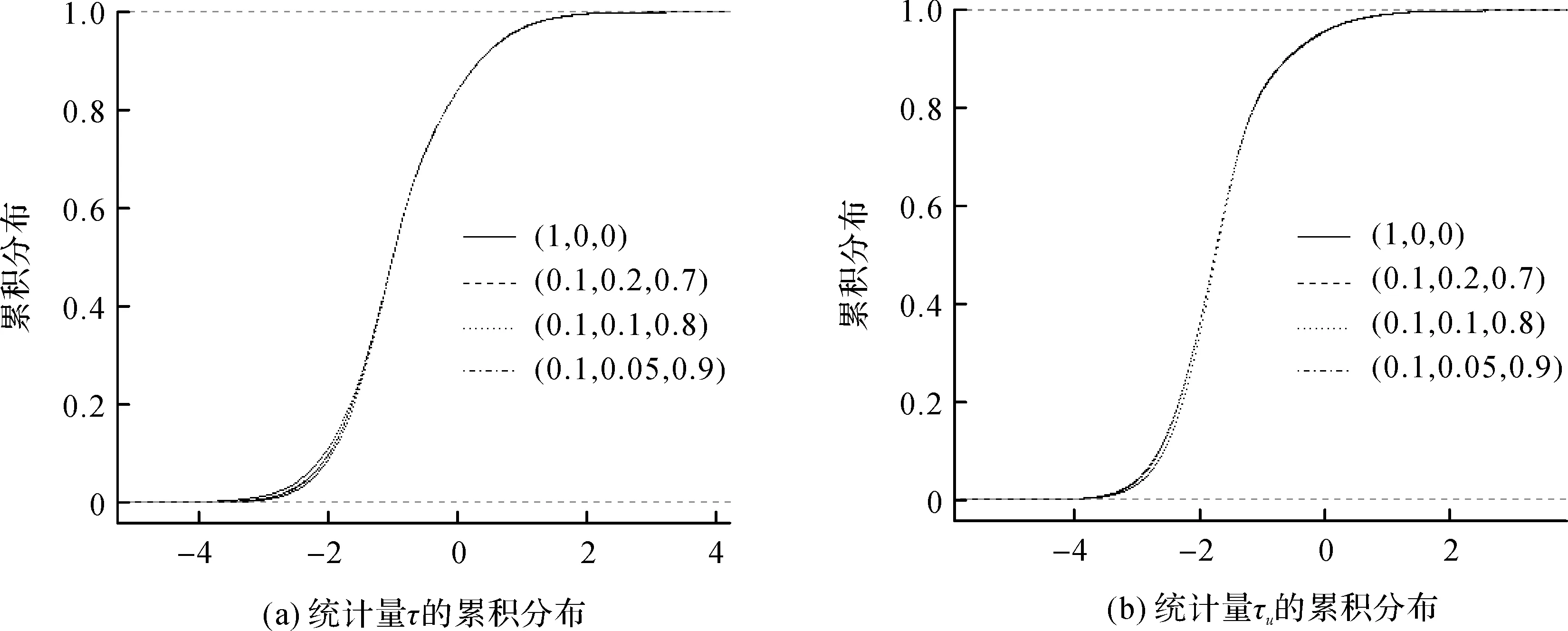
图1 不同系数(ω,α1,β1)下统计量τ和τu的累积分布Fig.1 Cumulative distributions of τ and τu for different coefficients (ω,α1,β1)

由于STAR模型的应用领域涉及很多宏观数据是小样本的情况，比如像失业率和利率等[5]77。接下来，在小样本的情况下，对各种数据生成过程中检验统计量临界值与渐进临界值进行比较。误差项中GARCH模型的参数设为(ω,α1,β1)=(0.1,0.1,0.8)，样本容量T设为50、100、200、1 000这4种情况。数据生成过程重复50 000次。图2给出了不同样本容量情况下检验统计量τ和τu的经验累积分布。对不同样本量而言，统计量τ和τu的经验累积分布非常接近。特别是对无漂移项的数据生成过程，样本容量的变化对临界值并没有造成很大的影响，所以渐进临界值可以用来对不同的样本进行检验。进一步，从图2可以看出，如果给定名义水平和该水平下的临界值，则不同样本量产生的实际拒绝水平与名义水平接近。所以渐进临界值表在小样本情况下对检验非线性平稳的ESTAR-GARCH模型仍然适用。

图2 不同样本量下统计量τ 和τu的累积分布Fig.2 Cumulative distributions of τ and τu for different sample sizes

为了评估在备择假设下即在平稳ESTAR过程中检验统计量的势，不妨设数据生成过程为

其中{et}～i.i.d.(0,1)且γ=-1。在实际应用中，通常设γ=-1(参见文献[19])。由于在实际应用中在给定γ=-1的情况下，θ的估计值通常都比较小(参见Kapetanios等[4]374)，所以在模拟过程中，仅考虑θ={0.01,0.05,0.1}的情况。表1～2中给出了检验统计量的势，并将它们与常规的DF检验统计量(记为DF)进行比较，检验的实际水平设为5%。从表中可以看出当θ较小时，无论(ω,α1,β1)如何取值，τ和τu比常规的DF具有更高的势。举个例子来说明，观察表1～2中当θ=0.01，(ω,α1,β1)=(0.1,0.2,0.7)时，样本量从50到100，统计量τ的势从0.376 9到0.856 6，而DF检验的势是0.217 4到0.762 6；统计量τu的势从0.211 6到0.531 4，而DF检验的势是0.118 2 到0.329 0。当然，当θ取值变大，因为模型渐进线性，DF检验统计量会有更高的势。当样本量比较大时(比如T=200)，可以看出，所有检验统计量的势都接近1。对比表1和表2可以看出，在原始数据和去均值数据情况下，前者检验统计量的势更高。

表1 备择假设下统计量τ的势Table 1 Power of τ under alternative hypothesis

注：显著性水平为5%。

表2 备择假设下统计量τu的势Table 2 Power of τu under alternative hypothesis

3 结 论

在实际应用中，GARCH模型被广泛地应用于对经济(金融)时间序列波动性的研究，它能较好地解决波动群集问题, 即大(小)的波动后紧跟的是大(小)的波动。由于GARCH模型的系数是未知的，考虑了KSS型检验统计量来检验，检验功效及检验水平分析表明，该统计量具有良好的检验水平及较高的检验功效。因此，在应用中，无论数据生成过程中误差项是常数还是异方差情景，都可以通过模拟对临界值加以估计。从蒙特卡罗模拟可以得出，KSS型检验统计量比常规的DF检验量具有更高的检验功效，为误差项不独立(相依)的非线性ESTAR模型的单位根检验(对这种过程的购买力平价理论的检验)提供了一定的参考依据。

[1] KABIRI S, LOTFOLLAHZADEH T, SHAYESTEH M G, et al. Modelling and forecasting of signal-to-interference plus noise ratio in femtocellular networks using logistic smooth threshold autoregressive model[J]. IET Signal Processing,2015,9(1):48.

[2] CHEN R C Y, LEE C H. The influence of CSR on firm value: an application of panel smooth transition regression on Taiwan[J]. Applied Economics,2017,49(34):1.

[3] UBILAVA D, HELMERS C G. Forecasting ENSO with a smooth transition autoregressive model[J]. Environmental Modelling and Software Volume,2013,40(2):181.

[4] KAPETANIOS G, SHIN Y, SNELL A. Testing for a unit root in the nonlinear STAR framework[J]. Journal of Econometrics,2003,112(2):359.

[5] KRUSE R. A new unit root test against ESTAR based on a class of modified statistics[J]. Statistical Papers,2011,52(1):71.

[6] HANCK C. On the asymptotic distribution of a unit root test against ESTAR alternatives[J]. Statistics and Probability Letters,2012,82(2):360.

[7] 张凌翔,张晓峒. 单位根检验中的Wald统计量研究[J]. 数量经济技术经济研究,2009,26(7):146.

[8] 宫健,高铁梅,张泽.汇率波动对我国外汇储备变动的非对称传导效应：基于非线性LSTARX-GARCH模型[J].金融研究,2017(2):84.

[9] LING S Q, LI W K. Asymptotic inference for unit root processes with GARCH(1,1) errors[J]. Econometric Theory,2003,19(4):541.

[10] WANG G W. A note on unit root tests with heavy-tailed GARCH errors[J]. Statistics and Probability Letter,2006,76(10):1075.

[11] YUAN Y Z, ZHANG R M. Estimation for nearly unit root processes with GARCH errors[J]. Applied Mathematics: A Journal of Chinese University(Series B),2010,25(3):297.

[12] LUUKKONEN R, SAIKKONEN P, TERSVIRTA T. Testing linearity against smooth transition autoregressive models[J]. Biometrika,1988,75(3):491.

[13] YANG X R, ZHANG L X. A note on self-normalized Dickey-Fuller test for unit root in autoregressive time series with GARCH errors[J]. Applied Mathematics: A Journal of Chinese University(Series B),2008,23(2):197.

[14] HALL P, LUKACS E, BIRNBAUM Z W, et al. Martingale limit theory and its application[J]. Journal of the American Statistical Association,1980,78(78):301.

[15] MÜLLER U K, ELLIOTT G. Tests for unit roots and the initial condition[J]. Econometrica,2003,71(4):1269.

[16] PHILLIPS P C B, SOLO V. Asymptotics for linear processes[J]. The Annals of Statistics,1992,20(2):971.

[17] 孙荣恒. 随机过程及其应用[M]. 北京：清华大学出版社,2004.

[18] 严士健，刘秀芳. 测度与概率[M]. 北京：北京师范大学出版社,1994.

[19] TAYLOR M P, PEEL D A, SARNO L. Nonlinear mean-reversion in real exchange rates: toward a solution to the purchasing power parity puzzles[J]. International Economic Review,2001,42(4):1015.